AP Board 10th Class Maths Solutions Chapter 10 క్షేత్రమితి Exercise 10.4

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.4

ప్రశ్న 1.
4.2 సెం.మీ. వ్యాసార్ధము కల్గిన ఒక లోహపు గోళంను – కరిగించి 6 సెం.మీ. వ్యాసార్ధము కల్గిన స్టూపముగా . మలిస్తే, ఆ స్థూపము యొక్క ఎత్తు ఎంత ?
సాధన.

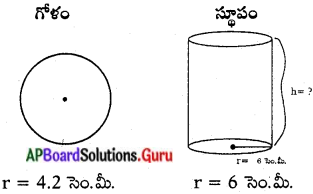
లెక్క ప్రకారం, గోళం యొక్క ఘనపరిమాణం = స్థూపం యొక్క ఘనపరిమాణం
⇒ \(\frac{4}{3}\) πr³ = πr₁²h
⇒ \(\frac{4}{3}\) r³ = r₁²h
⇒ \(\frac{4}{3}\) × 4.2 × 4.2 × 4.2 = 6 × 6 × h
⇒ h = \(\frac{98.784}{36}\) = 2.744
∴ స్థూపం యొక్క ఎత్తు = 2.744 సెం.మీ.

ప్రశ్న 2.
6 సెం.మీ., 8 సెం.మీ. మరియు 10 సెం.మీ. వ్యాసార్ధములు కల్గిన లోహపు గోళములను కరిగించి ఒక పెద్ద లోహపు గోళముగా మలిస్తే దాని యొక్క వ్యాసార్ధము ఎంత ? –
సాధన.

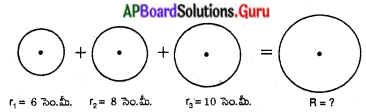
లెక్క ప్రకారం, 6 సెం.మీ., 8 సెం.మీ., 10 సెం.మీ.లు వ్యాసార్ధాలుగా గల గోళాల ఘనపరిమాణముల మొత్తం = పెద్ద గోళం ఘనపరిమాణం
⇒ \(\frac{4}{3}\) πr₁³ + \(\frac{4}{3}\) πr₂³ + \(\frac{4}{3}\) πr₃³ = \(\frac{4}{3}\) πR³

⇒ \(\frac{4}{3}\) π[r₁³ + r₂³+ r₃³] = \(\frac{4}{3}\) × π × R³

⇒ r₁³ + r₂³ + r₃³ = R³

⇒ 6³ + 8³ + 10³ = R³
⇒ 216 + 512 + 100 = R³
⇒ R³ = 1728
⇒ R = 123
∴ R = 12 (∵ ఘాతాంకాలు సమానమైన భూములు కూడా సమానాలే)
∴ పెద్ద గోళం వ్యాసార్ధం (R) = 12 సెం.మీ.

ప్రశ్న 3.
20 మీటర్లు లోతు, 7 మీటర్ల వ్యాసము గల ఒక గొయ్యిని త్రవ్వగా వచ్చిన మట్టిని 22 మీటర్లు × 14 మీటర్లు కొలతలుగా ఒక ప్లాట్ ఫాంగా ఏర్పరిస్తే దాని యొక్క ఎత్తు ఎంత ?
సాధన.
త్రవ్విన భూమి యొక్క ఘనపరిమాణం = πr²h
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 20 = 770 m
ప్లాట్ ఫాం ఎత్తు = h m అనుకొనుము
∴ 22 × 14 × h = \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) × 20
h = \(\frac{35}{14}=\frac{5}{2}=2 \frac{1}{2}\) m
∴ ప్లాట్ ఫారమ్ ఎత్తు 2\(\frac{1}{2}\) m.

ప్రశ్న 4.
14 మీటర్లు వ్యాసము, 15 మీటర్ల లోతు కల్గిన ఒక బావిని త్రవ్వగా వచ్చిన మట్టిని 7 మీటర్ల వెడల్పు కల్గిన ఒక వృత్తాకార కంకణముగా ఏర్పరిస్తే దాని యొక్క
ఎత్తు ఎంత ?
సాధన.

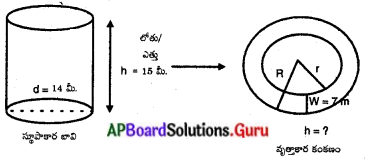
లెక్క ప్రకారం, స్థూపాకార బావి నుండి తీసిన మట్టి ఘనపరిమాణం = వృత్తాకార కంకణంగా ఏర్పర్చిన ఆ మట్టి ఘనపరిమాణం.
స్థూపాకార బావి వ్యాసార్ధం r = \(\frac{\mathrm{d}}{2}=\frac{14}{2}\) = 7 మీ.
బావి లోతు/ఎత్తు (h) = 15 మీ.
∴ స్థూపాకార బావి నుండి త్రవ్విన మట్టి ఘనపరిమాణం V₁ = πr²h
= \(\frac{22}{7}\) × 7 × 7 × 15
బావి నుండి త్రవ్వి తీసిన మట్టిని వృత్తాకార కంకణంగా ఏర్పర్చిన దాని వెడల్పు (w) = R – r = 7 మీ.
దాని ఎత్తు (h) = ?
∴ కంకణాకార మట్టి ఘనపరిమాణం (V₂) = π
V₂ = \(\frac{22}{7}\) × (R + r) (R – r) × h
= \(\frac{22}{7}\) × (14 + 7) × 7 × h
(∵ బావి వ్యాసార్ధం కంకణం యొక్క లోపలి వ్యాసార్ధం (r) = 7 మీ.)
(∵ R = W + r = 7 + 7 = 14 మీ.)
లెక్క ప్రకారం, V₁ = V₂
⇒ \(\frac{22}{7}\) × 7 × 7 × 15 = \(\frac{22}{7}\) × (14 + 7) × 7 × h
⇒ 7 × 15 = 21 × h
⇒ h = 5 మీ.
∴ వృత్తాకార కంకణంగా ఏర్పర్చిన మట్టి దిబ్బ ఎత్తు (b) = 5 మీ.

ప్రశ్న 5.
12 సెం.మీ. వ్యాసము, 15 సెం.మీ. ఎత్తు కల్గిన ఒక క్రమవృత్తాకార స్థూపాకృతి పాత్రలో నిండుగా ఐస్ క్రీం ఉన్నది. దానిని 12 సెం.మీ. ఎత్తు, 6 సెం.మీ. భూవ్యాసముగా కల్గిన శంఖువు ఆకార వస్తువు (కోన్)లో పైభాగము అర్ధగోళాకారంలో ఉండే విధముగా ఐస్ క్రీంను నింపితే, ఆ మొత్తం ఐస్ క్రీంను నింపడానికి కావలసిన కోన్ల సంఖ్య ఎంత ?
సాధన.

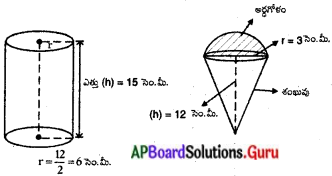
ఇచ్చినవి :
క్రమవృత్తాకార స్థూపాకృతి యొక్క వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{12}{2}\) = 6 సెం.మీ.
ఎత్తు (h) = 15 సెం.మీ.
అర్ధగోళం/శంఖువు యొక్క వ్యాసార్ధాలు (r) = \(\frac{\mathrm{d}}{2}=\frac{6}{2}\) = 3 సెం.మీ.
శంఖువు ఎత్తు (h) = 12 సెం.మీ.
శంఖువు పైభాగం అర్ధగోళాకారంలో ఉండే విధంగా ఐస్ క్రీంను నింపితే, మొత్తం స్థూపాకృతిని ఐస్ క్రీంతో నింపుటకు కావలసిన కోన్ల సంఖ్య –

కావలసిన, కోన్ల సంఖ్య = 10.

ప్రశ్న 6.
5.5 సెం.మీ. × 10 సెం.మీ. × 3.5 సెం.మీ. కొలతలు కలిగిన దీర్ఘఘనముగా మార్చడానికి 1.75 సెం.మీ. వ్యాసము, 2 మి.మీ. మందము కల్గిన ఎన్ని వెండి నాణెములు అవసరమవుతాయి ?
సాధన.
కరిగించవలసిన వెండి నాణేల సంఖ్య = n అనుకొనుము.
‘n’ సంఖ్యగల వెండి నాణేల ఘనపరిమాణం = దీర్ఘఘనాకారం యొక్క ఘనపరిమాణం
⇒ n × πr²h = lbh
⇒ n × \(\frac{22}{7} \times\left(\frac{1.75}{2}\right)^{2} \times \frac{2}{10}\)
= 5.5 × 10 × 3.5 (∵ మందంఎత్తు (h) = 2 మి.మీ. = \(\frac{2}{10}\) సెం.మీ.)
⇒ n × \(\frac{22}{7} \times \frac{1.75}{2} \times \frac{1.75}{2} \times \frac{2}{10}\) = 55 × 3.5
n = \(\frac{7 \times 35 \times 5}{1.75 \times 1.75}\)

= \(\frac{175 \times 7}{1.75 \times 1.75}=\frac{100}{0.25}\) = 400
∴ n = 400
∴ కావలసిన వెండి నాణేల సంఖ్య = 400.

ప్రశ్న 7.
ఒక పాత్ర తిరగబడిన శంఖువు ఆకారంలో ఉన్నది. దాని ఎత్తు 8 సెం.మీ. పై భాగము వా త , 5 సెం.మీ. పాత్ర పూర్తిగా నీటితో నింపబడి యున్నలు. దానిలో 0.5 సెం.మీ. వ్యాసార్ధము కల్గిన ఘనగోళమును వేస్తే పాత్రలో యున్న నీటిలో 7వ వంతు పొర్లి బయటికి .. వస్తుంది. అయినచో పాత్రలో వేయగల్గిన మొత్తము ఘనపు గోళముల సంఖ్య ఎంత ?
సాధన.

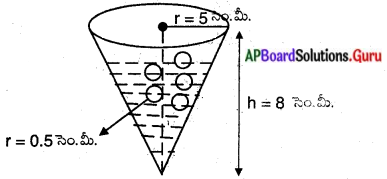
ఇవ్వబడినవి : పై పటం నుండి,
శంఖువు ఆకార పాత్ర వ్యాసార్ధం (r) = 5 సెం.మీ.
ఎత్తు (h) = 8 సెం.మీ.
గోళం వ్యాసార్ధం (r) = 0.5 సెం.మీ. = \(\frac{1}{2}\) సెం.మీ.
శంఖువాకార పాత్రలో ఘనగోళమును వేస్తే దానిలోని నీరు \(\frac{1}{4}\) వంతు పొర్లి బయటకు వచ్చినది అంటే గోళముల ఘనపరిమాణాల మొత్తం శంఖువు ఘనపరి మాణంలో \(\frac{1}{4}\) వ వంతు అని అర్థం.
∴ శంఖువాకార పాత్రలో వేయదగు గోళముల సంఖ్య

కావలసిన ఘనపు గోళముల సంఖ్య = 100.

ప్రశ్న 8.
28 సెం.మీ. వ్యాసము కల్గిన ఒక ఘనపు గోళమును కరిగించి 45 సెం.మీ. వ్యాసం, 8 సెం.మీ. ఎత్తు కల్గిన శంఖువులుగా మారిస్తే ఏర్పడే శంఖువుల సంఖ్య ఎంత ?
సాధన.
చిన్న శంఖువుల సంఖ్య = ‘n’ అనుకొనుము.
లెక్క ప్రకారము .
⇒ ‘n’ శంఖువుల ఘనపరిమాణం = గోళం యొక్క ఘనపరిమాణం
శంఖువు : వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}\)
= \(\frac{4 \frac{2}{3}}{2}\)
= \(\frac{\frac{14}{3}}{2}=\frac{7}{3}\) సెం.మీ.
ఎత్తు (h) = 3 సెం.మీ.
గోళం : వ్యాసార్థం (r) = \(\frac{\mathrm{d}}{2}=\frac{28}{2}\) = 14 సెం.మీ
∴ లెక్క ప్రకారం
⇒ n × \(\frac{1}{3}\) πr₁²h = \(\frac{4}{3}\) πr₂²
⇒ n × \(\frac{1}{3} \times \frac{22}{7} \times \frac{7}{3} \times \frac{7}{3} \times 3\) = \(\) × (14)³
⇒ n × \(\frac{7}{3}\) × 7 = 4 × 14 × 14 × 14
⇒ n = 3 × 4 × 14 × 2 × 2
∴ n = 672
∴ కావలసిన శంఖువుల సంఖ్య (n) = 672.