AP Board 10th Class Maths Solutions Chapter 11 త్రికోణమితి InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 11 త్రికోణమితి InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 11th Lesson త్రికోణమితి InText Questions

ఇవి చేయండి:

క్రింద ఇచ్చిన త్రిభుజాలలో ఇచ్చిన కోణాల ఆధారంగా “కర్ణం”, “ఎదుటి భుజము” మరియు “ఆసన్న భుజము” లను గుర్తించి రాయండి. (పేజీ నెం. 271)

ప్రశ్న 1.
కోణం R పరంగా

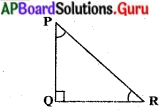
సాధన.
కోణం R పరంగా .
∆PQR లో PQ = ఎదుటి భుజము
QR = ఆసన్న భుజము మరియు
PR= కర్ణము

ప్రశ్న 2.
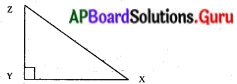
(i) కోణం X పరంగా
(ii) కోణం Y పరంగా

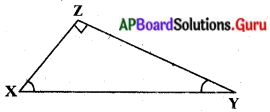
సాధన.
(i) ∆XYZ లో,
కోణం X పరంగా ఎదుటి భుజము = YZ
ఆసన్న భుజము = XZ మరియు
కర్ణము = XY

(ii) ∆XYZ లో, కోణం Y పరంగా
ఎదుటి భుజము = XZ
ఆసన్న భుజము = YZ మరియు
కర్ణము = XY.

ప్రశ్న 3.
పక్కనున్న లంబకోణ త్రికోణంలో (పేజీ నెం. 274)
(i) sin C
(ii) cos C మరియు
(iii) tan C లను కనుగొనుము

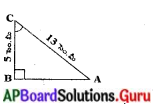
సాధన.
పైథాగరస్ సిద్ధాంతము నుండి
AC² = AB² + BC²
13² = AB² + 5²
AB² = 169 – 25
AB² = 144
AB = √144 = 12 సెం.మీ.

(i) sin C =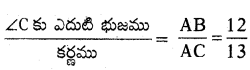

(ii) cos C =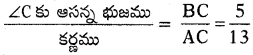

(iii) tan C =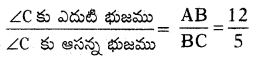

ప్రశ్న 4.
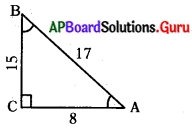
ఒక త్రిభుజము XYZలో, 4 Y లంబకోణము మరియు XZ = 17 సెం.మీ., YZ = 15 సెం.మీ. (పేజీ నెం. 274)
(i) sin x
(ii) cos Z
(iii) tan X లను కనుగొనుము.
సాధన.
∆XYZలో, ∠Y లంబకోణము మరియు XZ = 17 సెం.మీ., YZ = 15 సెం.మీ.
పైథాగరస్ సిద్ధాంతము నుండి

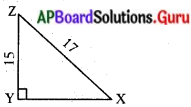
XZ² = YZ² + XY²
17² = 15² + XY²
XY² = 17² – 15²
XY² = = 289 – 225
XY² = 64
XY = 164 = 8 సెం.మీ.

(i) sin X =
= \(\frac{\mathrm{YZ}}{\mathrm{XZ}}=\frac{15}{17}\)

(ii) cos Z =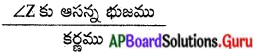
= \(\frac{\mathrm{YZ}}{\mathrm{XZ}}=\frac{15}{17}\)

(iii) tan X =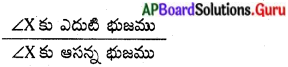
= \(\frac{Y Z}{X Y}=\frac{15}{8}\).

ప్రశ్న 5.
త్రిభుజం PQR లో Q లంబకోణము మరియు ∠P విలువ X మరియు PQ = 7 సెం.మీ. మరియు QR = 24 సెం.మీ. అయిన sin x మరియు cos x ల విలువలు కనుగొనుము. (పేజీ నెం. 274)
సాధన.
ఇచ్చిన లంబకోణ త్రిభుజము PQRలో Qలంబకోణము మరియు ∠P విలువ X మరియు PQ = 7 సెం.మీ. మరియు QR = 24 సెం.మీ.
పైథాగరస్ సిద్ధాంతం ప్రకారం

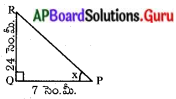
PR² = PQ² + QR²
= 7² + 24²
PR² = 49 + 576
PR² = 625
PR = √625 = 25 సెం.మీ.
sin x = \(\frac{\mathrm{QR}}{\mathrm{PR}}=\frac{24}{25}\)
cos x = \(\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{7}{25}\)

ప్రయత్నించండి:

ప్రశ్న 1.
ఈ క్రింద ఇచ్చిన త్రిభుజంలో ఇచ్చిన కోణాల పరంగా “కర్ణం”, “ఎదుటి భుజం” మరియు “ఆసన్న భుజం” లను కనుగొనండి. (పేజీ నెం. 271)

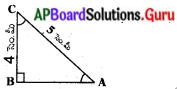
1. కోణం C పరంగా
2. కోణం A పరంగా మీరేం గమనించారు ?
కోణం A యొక్క ఎదుటి భుజము మరియు కోణం C యొక్క ఆసన్న భుజానికి ఏమైనా సంబంధం ఉందా ? ఇంకా, ఒక బలమైన లోహపు వైర్ ఆధారంగా ఒక స్థంభాన్ని నిలబెడుతున్నామను కుందాం. స్థంభం ఎత్తు మరియు వైర్ పొడవుకు ఏదైనా సంబంధం ఉందనుకుంటున్నారా? ఇక్కడ మనం త్రిభుజంలోని భుజాల మధ్యన సంబంధాన్ని వాటి కోణాల ఆధారంగా అవగాహన చేసుకోవడానికి ప్రయత్నిద్దాం.
సాధన.
పైథాగరస్ సిద్ధాంతము నుండి
AC² = AB² + BC²
(5)² = AB² + 4²
25 = AB² + 16
AB² = 25 – 16
AB² = 9
AB = √9 = ± 3 = 3
∆ABC నుండి, కోణం ‘C’ పరంగా
ఎదుటి భుజము = AB = 3 సెం.మీ.
ఆసన్న భుజము = BC = 4 సెం.మీ.
కర్ణము = AC = 5 సెం.మీ.
∆ABC నుండి, కోణం ‘A’ పరంగా
ఎదుటి భుజము = BC = 4 సెం.మీ.
ఆసన్న భుజము = AB = 3 సెం.మీ.
కర్ణము = AC = 5 సెం.మీ.,
మనం తీసుకున్న కోణాన్ని బట్టి ఎదుటి భుజం, ఆసన్న భుజం మారుతూ ఉంటాయి. కానీ కర్ణం మాత్రం మారదు. ఒక బలమైన లోహపు వైర్ ఆధారంగా ఒక స్థంభాన్ని నిలబెడితే ఒక లంబకోణ త్రిభుజం ఏర్పడుతుంది.. పైథాగరస్ సిద్ధాంతం నుండి మనకు కావలసింది కనుక్కోవచ్చు.

ప్రశ్న 2.
ఒక లంబకోణ త్రిభుజం ABC లో C లంబకోణం. BC + CA = 23 సెం.మీ. మరియు BC – CA = 7 సెం.మీ. అయిన sin A మరియు tan B లను కనుగొనుము. (పేజీ నెం. 274)
సాధన.
లంబకోణ త్రిభుజము ABC లో, ‘C’ వద్ద లంబకోణం కలదు.

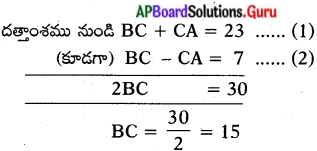
BC = 15 సెం.మీ.
BC = 15 ను (1) లో ప్రతిక్షేపించగా
BC + CA = 23
CA = 23 – BC = 23 – 15
CA = 8 సెం.మీ
పైథాగరస్ సిద్ధాంతము ప్రకారము ∆ABCలో

AB² = AC² + BC²
= 8² + 15²
= 64 + 225 = 289
AB = √289 = 17 సెం.మీ.
sin A = \(\frac{B C}{A B}=\frac{15}{17}\)
tan B = \(\frac{A C}{B C}=\frac{8}{15}\)

ప్రశ్న 3.
sec A మరియు cot A ల భుజాల నిష్పత్తులు . ఏమౌతాయి ? (పేజీ నెం. 275)
సాధన.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
(i) ఏదో ఒక విలువ Xకు sinx= 4 సాధ్యమా? ఎందుకు?
(ii) sin A మరియు cos Aల విలువలు ఎల్లప్పుడు 1 కంటే తక్కువగా ఉంటాయి. ఎందుకు ?
(iii) tan A అంటే tan మరియు A ల లబ్దము. పై ప్రశ్నలను మిత్రులతో చర్చించండి. (పేజీ నెం. 274)
సాధన.
(i) ఏదో ఒక విలువ x కు sin x = \(\frac{4}{3}\) కాదు (అసాధ్యము).
sin x =
ఇక్కడ కర్ణము కన్నా ఎదుటి భుజం పెద్దదిగా కలదు. ఇది లంబకోణ త్రిభుజంలో మిక్కిలి పెద్ద భుజం కర్ణము అనడానికి విరుద్దత. కావున
sin x = \(\frac{4}{3}\) కావడం అసాధ్యము.

(లేదా)

పై త్రిభుజంలో, XZ > YZ మరియు XZ > XY.
sin x =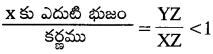
[:: XZ > YZ, లవంకన్నా హారం పెద్దది. కావున \(\frac{\mathrm{YZ}}{\mathrm{XZ}}\) ఒక క్రమభిన్నము. దీని విలువ ఎల్లప్పుడు 1 కన్నా తక్కువ]
కాని లెక్క ప్రకారం sin x = \(\frac{4}{3}\) విలువ 1 కన్నా ఎక్కువ కావున ఇది అసాధ్యము.

(ii) sin A = ∠Aకు ఎదుటి భుజం / కర్ణము

cos A = ∠Aకు ఆసన్న భుజం / కర్ణము
లంబకోణ త్రిభుజంలో ఎదుటి భుజం, మరియు ఆసన్న భుజములు ఎల్లప్పుడు కర్ణం కన్నా చిన్నవి.
కాబట్టి sin A, cos A లు ఎల్లప్పుడు 1 కంటే . తక్కువగా ఉంటాయి.

(iii) tan A అనగా A కోణమునకు ఎదురుగా గల భుజం మరియు ఆసన్న భుజముల నిష్పత్తి అని అర్థం. అంతేకాని tan మరియు A ల లబ్దము కాదు.

ప్రశ్న 2.
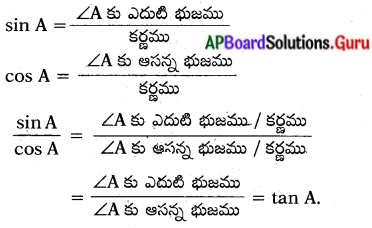
\(\frac{\sin A}{\cos A}\) ఈ విలువ tan A అవుతుందా ? (పేజీ నెం. 275)
పాదన.
\(\frac{\sin A}{\cos A}\) = tan A అగును.
నిరూపణ :

ప్రశ్న 3.
\(\frac{\cos A}{\sin A}\) ఈ విలువ cot A అవుతుందా ? (పేజీ నెం. 275)
సాధన.
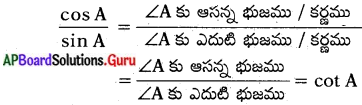
\(\frac{\cos A}{\sin A}\) = cot A అగును.
నిరూపణ :
cos A = ∠A కు ఆసన్న భుజము / కర్ణము
sin A = ∠A కు ఎదుటి భుజము / కర్ణము
cos A _ LAకు ఆసన్న భుజము / కర్ణము sin A – LA కు ఎదుటి భుజము / కర్ణము

ఇవి చేయండి:

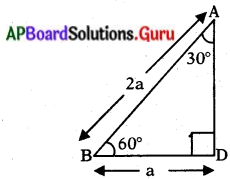
ప్రశ్న 1.
cosec 60°, sec 30° మరియు cot 60°ల , విలువలు కనుగొనండి. (పేజీ నెం. 279)
సాధన.
క్రింది పటం నుండి
ABDలో AB = 2a మరియు – BD = a యూనిట్లు
అప్పుడు AD² = AB² – BD² (పైథాగరస్ సిద్ధాంతం ప్రకారం)
= (2a)² – (a)².
AD² = 3a²
AD = √3a² = √3a

త్రికోణమితీయ నిష్పత్తుల నిర్వచనాల ఆధారంగా
sin 60° = \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{a} \sqrt{3}}{2 \mathrm{a}}=\frac{\sqrt{3}}{2}\)

cos 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{\mathrm{a}}{2 \mathrm{a}}=\frac{1}{2}\)
ఇదే విధంగా
tan 60° = \(\frac{\sin 60^{\circ}}{\cos 60^{\circ}}=\frac{\sqrt{3} / 2}{1 / 2}\) = √3

cosec 60° = \(\frac{-1}{\sin 60^{\circ}}=\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2}{\sqrt{3}}\)

sec 60° = \(\frac{1}{\cos 60^{\circ}}=\frac{1}{\frac{1}{2}}=\frac{2}{1}\) = 2

cot 60° = \(\frac{1}{\tan 60^{\circ}}=\frac{1}{\sqrt{3}}\).

ప్రయత్నించండి:

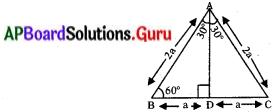
ప్రశ్న 1.
sin 30°, cos 30°, tan 30°, cosec 309, sec 30° మరియు cot 30° విలువలను కనుక్కోండి. (పేజీ నెం. 279)
సాధన.

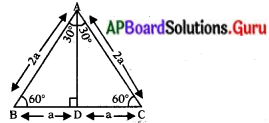
ఒక సమబాహు త్రిభుజం ABC ని తీసుకోండి. ఇందులో ప్రతి కోణం 60° ఉంటుంది.
కావున ∠A = ∠B = ∠C = 60° మరియు AB = BC = CA = 2a యూనిట్లు అనుకోండి.
శీర్షం ‘A’ నుండి. భుజం BC పైకి ఒక లంబం AD ను పై పటంలో చూపినట్లుగా గీయండి.
ఈ లంబం AD, కోణం A యొక్క “కోణ సమద్వి ఖండన రేఖ” గా మరియు భుజం BC యొక్క “సమద్వి ఖండన రేఖ”గా కూడా పనిచేస్తుంది.
∴ ∠BAD = ∠CAD = 30°.
BC ను D బిందువు రెండు సమాన భాగాలుగా చేస్తుంది. కావున BD = \(\frac{1}{2}\) BC = \(\frac{2 \mathrm{a}}{2}\) = a యూనిట్లు.

లంబకోణ త్రిభుజం ABD లో

AB = 2a మరియు BD = a యూనిట్లు .అప్పుడు AD² = AB² – BD²
(పైథాగరస్ సిద్ధాంతం ప్రకారం)
= (2a)² – a² = 3a²
AD² = 3a²
∴ AD = a√3
∆ADB లో BD = a, AD = √3a మరియు కర్ణము = AB = 2a మరియు ∠DAB = 30°.
త్రికోణమితీయ నిష్పత్తుల నిర్వచనాల ప్రకారం
sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{\mathrm{a}}{2 \mathrm{a}}=\frac{1}{2}\)

cos 30° = \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\sqrt{3} \mathrm{a}}{2 \mathrm{a}}=\frac{\sqrt{3}}{2}\)

tan 30° = \(\frac{B D}{A D}=\frac{a}{\sqrt{3} a}=\frac{1}{\sqrt{3}}\)

cosec 30° = \(\frac{1}{\sin 30^{\circ}}\) = 2

sec 30° = \(\frac{1}{\cos 30^{\circ}}=\frac{2}{\sqrt{3}}\)

cot 30° = \(\frac{1}{\tan 30^{\circ}}\) = √3

ప్రశ్న 2.
tan 90°, cosec 90°, sec 90° మరియు cot 90° విలువలను కనుగొనండి. (పేజీ నెం. 281)
సాధన.

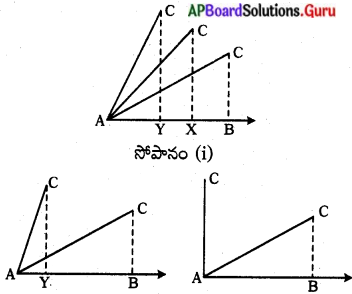
AB కిరణంపై AC చేసే AD కోణాన్ని పెంచుతూ పోతే, AB పై ‘C’ ఎత్తు పెరుగుతూ, బిందువు ‘B’ నుండి X కు ఆ తర్వాత Yకు మారుతూ పోతుంది.
A పెరుగుతూ పోతుంటే. ఎదుటి భుజం పెరుగుతూ, ఆసన్న భుజం తగ్గుతూ వుంటుంది. ఒక సమయానికి కోణం విలువ 90°లకు చేరుతుంది.
ఆ సందర్భంలో A, B ను చేరుతుంది. AC, BC తో కలిసిపోతుంది. .అనగా కోణం విలువ 90° అయినపుడు భూమి (ఆసన్న భుజం) విలువ సున్నా అయి, BC (ఎదుటి భుజం) విలువ క్రమంగా పెరుగుతూ. AC కు సమానమవుతుంది. అనగా ‘r’కు సమానమవుతుంది.

∆ ABC లో
sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) మరియు cos A = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
కోణం A = 90° అయిన AB = 0 మరియు AC = BC = r; అపుడు sin 90° = \(\frac{\mathrm{r}}{\mathrm{r}}\) = 1 మరియు cos 90° = \(\frac{0}{\mathrm{r}}\) = 0

tan 90° = \(\frac{\sin 90^{\circ}}{\cos 90^{\circ}}=\frac{1}{0}\) నిర్వచించబడదు.

cosec 90° = \(\frac{1}{\sin 90^{\circ}}=\frac{1}{1}\) = 1

sec 90° = \(\frac{1}{\cos 90^{\circ}}=\frac{1}{0}\) = నిర్వచించబడదు.

cot 90° = \(\frac{1}{\tan 90^{\circ}}=\frac{1}{\frac{1}{0}}=1 \times \frac{0}{1}\) = 0.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
ఈ క్రింది వాటిని మీ స్నేహితులతో చర్చించండి. cosec 0° = \(\frac{1}{\sin 0^{\circ}}\) ఇది నిర్వచింపబడుతుందా? ఎందుకు ? (పేజీ నెం. 280)
సాధన.
sin 0° = 0
cosec 0° = \(\frac{1}{\sin 0^{\circ}}=\frac{1}{0}\) = నిర్వచింపబడదు
కారణము :
‘0’ తో భాగహారము సాధ్యపడదు కనుక.

ప్రశ్న 2.
cot 0° = \(\frac{1}{\tan 0^{\circ}}\)నిర్వచింపబడుతుందా? ఎందుకు? (పేజీ నెం. 281)
సాధన.
tan 0° విలువ ‘0’ కావున
cot 0° = \(\frac{1}{\tan 0^{\circ}}=\frac{1}{0}\) (నిర్వచింపబడదు) ‘
కారణము : ‘0’ తో భాగహారము సాధ్యపడదు కాబట్టి,

ప్రశ్న 3.
sec 0° = 1. ఎందుకు ? (పేజీ నెం. 281)
సాధన.
దత్తాంశము నుండి sec 0° = \(\frac{1}{\cos 0^{\circ}}\)
[:: cos 0° = 1]
= \(\frac{1}{1}\) = 1.

ప్రశ్న 4.
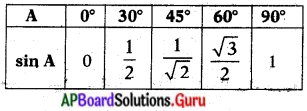
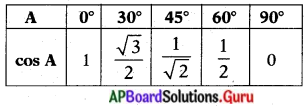
కోణం A విలువ 0° నుండి 90° కు పెరుగుతూ పోతుంటే sin A మరియు cos A విలువలు ఎలా మారుతూ ఉంటాయి ? (పై పట్టికను గమనించండి)
(i) A ≥ B అయిన sin A ≥ sin B అనడం సబబేనా ?
(ii) A ≥ Bఅయిన cos A ≥ cos B అనడం సబబేనా? చర్చించండి. (పేజీ నెం. 282)
సాధన.
(i) ఇచ్చిన ప్రవచనము .
“A ≥ B అయిన sin A ≥ sin B”. ఈ ప్రవచనము సత్యమే అనుటను క్రింది పట్టిక తెల్పుచున్నది. ‘A’ కోణము విలువ పెరిగే కొలదీ దాని sine విలువ పెరుగుచుండును.

దీనిని క్రింది పట్టికలో గమనించవచ్చును. A | 0 | 30 | 450 | 60° | 90° |

(ii) ఇచ్చిన ప్రవచనము
“A ≥ B అయిన. cos A ≥ cos B”. ఈ ప్రవచనము అసత్యము. ఎందుకనగా ‘A’ కోణము పెరిగే కొలదీ దాని cosine విలువ తగ్గును.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
θ యొక్క ఏ లఘుకోణ విలువక
(i) \(\frac{\cos \theta}{1-\sin \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 4 సత్యమౌతుంది ? పై సమీకరణం 0° ≤ θ ≤ 90° లలో ఏ విలువలకు నిర్వచించబడదు ? (పేజీ నెం. 285)
సాధన.
దత్తాంశము :
\(\frac{\cos \theta}{1-\sin \theta}+\frac{\cos \theta}{1+\sin \theta}\) = 4

⇒ \(\frac{\cos \theta(1+\sin \theta)+\cos \theta(1-\sin \theta)}{(1-\sin \theta)(1+\sin \theta)}=\frac{4}{1}\)

⇒ \(\begin{aligned}
&\cos \theta+\cos \theta \cdot \sin \theta+\\
&\frac{\cos \theta-\cos \theta \cdot \sin \theta}{1-\sin ^{2} \theta}=\frac{4}{1}
\end{aligned}\)
[∵ (a – b) (a + b) = a² – b²]

⇒ \(\frac{2 \cos \theta}{\cos ^{2} \theta}=\frac{4}{1}\)

⇒ \(\frac{2}{\cos \theta}=\frac{4}{1}\)
⇒ cos θ = \(\frac{2}{4}=\frac{1}{2}\)
⇒ cos θ = cos 60° (∵ cos 60° = 1/2)
⇒ θ = 60°
∴ θ = 60°ల వద్ద ఇచ్చిన దత్తాంశము సత్యము.

ప్రశ్న 2.
A యొక్క (0° ≤ A ≤ 90° యొక్క తెలిసిన అన్ని విలువలకు కింది సూత్రాలు సమంజసమేనా ? సరిచూడండి. (పేజీ నెం. 286)
(i) sin (90° – A) = cos A
(ii) cos (90° – A) = sin A
(iii) tan (90° – A) = cot A మరియు
(iv) cot (90° – A) = tan A
(v) sec (90°- A) = cosec A
(vi) cosec (90°- A) = sec A
సాధన.
A = 30° అనుకొనుము
(i) sin (90° – A) = cos A
⇒ sin (90° – 30°) = cos 30°
⇒ sin 60° = cos 30° = \(\frac{\sqrt{3}}{2}\)

(ii) cos (90° – A) = sin A.
⇒ cos (90° – 30°) = sin 30°
⇒ cos 60° = sin 30° = \(\frac{1}{2}\)

(iii) tan (90° – A) = cot A
⇒ tan (90° – 30°) = cot 30°
⇒ tan 60° = cot 30° = √3

(iv) cot (90° – A) = tan A.
⇒ cot (90° – 30°) = tan 30°
⇒ cot 60° = tan 30° = \(\frac{1}{\sqrt{3}}\)

(v) sec (90° – A) = cosec A
⇒ sec (90° – 30°) = cosec 30°
⇒ sec 60° = cosec 30° = 2

(vi) cosec (90° – A) = sec A
⇒ cosec (90° – 30°) = sec 30°
⇒ cosec 60° = sec 30° = \(\frac{2}{\sqrt{3}}\)
∴ ‘A’ యొక్క తెలిసిన అన్ని విలువలకు పై సూత్రాలు.

ఇవి చేయండి:

(i) sinA= 15, అయిన cos A విలువ కనుగొనుము. (పేజీ నెం. 290)
సాధన.
sin A = \(\frac{15}{17}\)
cos A = \(\sqrt{1-\sin ^{2} A}\) [సర్వ సమీకరణం – I నుండి]
= \(\sqrt{1-\left(\frac{15}{17}\right)^{2}}\)
= \(\sqrt{1-\frac{225}{289}}=\sqrt{\frac{289-225}{289}}\)
∴ cos A = \(\sqrt{\frac{64}{289}}=\frac{8}{17}\)

(ii) tan x = \(\frac{5}{12}\), అయిన sec x విలువ కనుగొనుము. (పేజీ నెం. 290)
సాధన.
దత్తాంశము tan x = \(\frac{5}{12}\)
sec x = \(\sqrt{1+\tan ^{2} x}\)
[∵ సర్వసమీకరణం – II నుండి]
= \(\sqrt{1+\left(\frac{5}{12}\right)^{2}}\)

= \(\sqrt{1+\frac{25}{144}}\)

= \(\sqrt{\frac{144+25}{144}}=\sqrt{\frac{169}{144}}=\frac{13}{12}\)

∴ sec x = \(\frac{13}{12}\)

(iii) cosec θ = \(\frac{25}{7}\), అయిన cot θ విలువను కనుగొనుము. (పేజీ నెం. 290)
సాధన.
cosec θ = \(\frac{25}{7}\)
cot θ = √(cosec² θ – 1)
(సర్వసమీకరణం – III నుండి)
= \(\sqrt{\left(\frac{25}{7}\right)^{2}-1}\)

= \(\sqrt{\frac{625}{49}-\frac{1}{1}}\)

= \(\sqrt{\frac{625-49}{49}}\)

= \(\sqrt{\frac{576}{49}}=\frac{24}{7}\)
= \(\frac{24}{7}\).

ప్రయత్నించండి:

క్రింది వాటి విలువలను సకారణంగా కనుగొనుము.
(i) \(\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}\) (పేజీ నెం. 290)
సాధన.
\(\frac{\sin ^{2} 15^{\circ}+\sin ^{2} 75^{\circ}}{\cos ^{2} 36^{\circ}+\cos ^{2} 54^{\circ}}\)

= \(\frac{\sin ^{2} 15^{\circ}+\sin ^{2}\left(90^{\circ}-15^{\circ}\right)}{\cos ^{2} 36^{\circ}+\cos ^{2}\left(90^{\circ}-36^{\circ}\right)}\)

= \(\frac{\sin ^{2} 15^{\circ}+\cos ^{2} 15^{\circ}}{\cos ^{2} 36^{\circ}+\sin ^{2} 36^{\circ}}\)

[∵ sin (90° – θ) = cos θ
cos (90° – θ) = sin θ]
= \(\frac{1}{1}\) = 1 [∵ sin² θ + cos² θ = 1]

(ii) sin 5° cos 85* + cos 5° sin 85° (పేజీ నెం. 290)
సాధన.
sin 5° cos 85° + cos 5° sin 85°C
= sin 5°. cos (90° – 5°) + cos 5°. sin (90° – 5°)
= sin 5°. sin 5° + cos 5° . cos 5°
[∵ sin (90° – θ) = cos θ
cos (90° – θ) = sin θ]
= sin² 5° + cos² 5° = 1
[∵ sin² θ + cos² θ = 1]

(iii) sec 16°cosec 74° – cot 74° tan 16. (పేజీ నెం. 290)
సాధన.
sec 16° cosec 74° – cot 74° tan 16°
= sec 16°. cosec (90° – 16) – cot (90° – 169) . tan 16°
= sec 16°.sec 16° – tan 16°.tan 16°
[∵ cosec (90° – θ) = sec θ
cot (90° – θ) = tan θ]
= sec² 16° – tan² 16°
= 1 [∵ sec² θ – tan² θ = 1]

ఆలోచించి, చర్చించి, రాయండి:

0° ≤ A ≤ 90° అన్ని విలువలకు త్రికోణమితీయ సర్వసమీకరణాలు – సత్యమేనా ? (పేజీ నెం. 290)

(i) sec² A – tan² A = 1
సాధన.
ఇచ్చిన సర్వసమీకరణం : sec² A – tan² A = 1
A = 0° అనుకొనుము.
L.H.S. = sec² 0° – tan² 0°
= 1 – 0 = 1 = R.H.S
A = 90° అనుకొనుము.
tan A మరియు sec A విలువలను నిర్వచించలేము.
కావున ‘A’ యొక్క అన్ని విలువలకు (0° ≤ A ≤ 90°) ఈ సర్వసమీకరణము సత్యము.

(ii) cosec² A – cot² A = 1
సాధన.
ఇచ్చిన సర్వసమీకరణము : cosec² A – cot² A = 1
A = 0° అనుకొనుము
A = 0 అయిన cosec A మరియు cot Aల , విలువలను నిర్వచించలేము.
A = 90° అనుకొనుము
cosec A = cosec 90° = 1
cot A = cot 90° = 0
L.H.S. = 1² – 0²
= 1 – 0 = 1 = R.H.S.
∴ కావున ‘A’ యొక్క అన్ని విలువలకు (0° ≤ A ≤ 90°) ఇచ్చిన సర్వసమీకరణము సత్యము.

ఉదాహరణలు:

ప్రశ్న 1.
tan A = \(\frac{3}{4}\) అయిన కోణం A యొక్క మిగతా త్రికోణమితీయ నిష్పత్తులను కనుక్కోండి. (పేజీ నెం. 275)
సాధన.
tan A = \(\frac{3}{4}\) అని ఇవ్వబడింది.
మరయు tan A = Aకు ఎదుటి భుజము / Aకు ఆసన్న భుజము = \(\frac{3}{4}\)

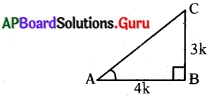
కావున ఎదుటి భుజము : ఆసన్న భుజము = 3 : 4
కావున కోణం A ఎదుటి భుజము = BC = 3k (k ఏదైనా ధనపూర్ణ సంఖ్య)
ఆసన్న భుజము = AB = 4k అనుకొనగా పైథాగరస్ సిద్ధాంతం ప్రకారం త్రిభుజం ABC లో
AC² = AB² + BC²
= (3k)² + (4k)² = 25k²
AC = √25k²
కర్ణం AC = 5k
ఇక మనం మిగతా త్రికోణమితీయ నిష్పత్తులను రాద్దాం .
sin A = \(\frac{3 k}{5 k}=\frac{3}{5}\) మరియు
cos A = \(\frac{4 k}{5 k}=\frac{4}{5}\)
cosec A = \(\frac{1}{\sin A}=\frac{5}{3},\)
sec A = \(\frac{1}{\cos A}=\frac{5}{4}\)
cot A = \(\frac{1}{\tan A}=\frac{4}{3}\)

ప్రశ్న 2.
∆ABC, ∆PQRలలో sin A = sin P అయ్యేటట్లు ∠A మరియు ∠P లు లఘుకోణాలు అయిన∠A = ∠P అని చూపుము. (పేజీ నెం. 276)
సాధన.
sin A = sin P అని ఇవ్వబడినది.
∆ABC నుండి sin A = \(\frac{\mathrm{BC}}{\mathrm{AC}}\) …………. (1)
∆PQR నుండి sin P = \(\frac{\mathrm{QR}}{\mathrm{PQ}}\) ……….. (2)
(1) & (2) ల నుండి \(\frac{B C}{A C}=\frac{Q R}{P Q}\)
\(\frac{B C}{A C}=\frac{Q R}{P Q}\) = k అనుకొనిన ……………. (3)

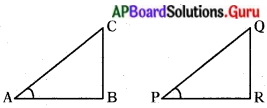
\(\frac{A B}{P R}=\frac{\sqrt{A C^{2}-B C^{2}}}{\sqrt{P Q^{2}-Q R^{2}}}=\frac{\sqrt{A C^{2}-k^{2} A C^{2}}}{\sqrt{P Q^{2}-k^{2} \cdot P Q^{2}}}\) (3 నుంచి) = \(\frac{\mathrm{AC}}{\mathrm{PQ}} \cdot\left(\frac{\sqrt{1-\mathrm{k}^{2}}}{\sqrt{1-\mathrm{k}^{2}}}\right)=\frac{\mathrm{AC}}{\mathrm{PQ}}\)

\(\frac{A C}{P Q}=\frac{A B}{P R}=\frac{B C}{Q R}\) అయిన ∆ABC ~ ∆PQR
∴ ∠A = ∠P.

ప్రశ్న 3.
P వద్ద లంబకోణం కల్గిన లంబకోణ త్రిభుజము PQRలో PQ = 29 యూనిట్లు, QR = 21 యూనిట్లు మరియు ∠PQR = θ, అయిన
(i) cos² θ + sin² θ మరియు
(ii) cos² θ – sin² θ విలువలు కనుగొనుము. (పేజీ నెం. 276)
సాధన.
త్రిభుజం PQR లో

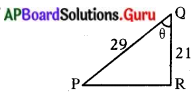
PR = \(\sqrt{\mathrm{PQ}^{2}-\mathrm{QR}^{2}}\)
= \(\sqrt{(29)^{2}-(21)^{2}}\)
= \(\sqrt{8(50)}\) = √400 = 20 యూనిట్లు
sin θ = \(\frac{\mathrm{PR}}{\mathrm{PQ}}=\frac{20}{29}\)
cos θ = \(\frac{\mathrm{QR}}{\mathrm{PQ}}=\frac{21}{29}\)

(i) cos² θ + sin² θ = \(\left(\frac{20}{29}\right)^{2}+\left(\frac{21}{29}\right)^{2}\)
= \(\frac{400+441}{841}\) = 1

(ii) cos² θ – sin² θ = \(\left(\frac{20}{29}\right)^{2}-\left(\frac{21}{29}\right)^{2}\)
= \(-\frac{41}{841}\)

ప్రశ్న 4.
B వద్ద లంబకోణం కల్గిన ∆ABC లో AB = 5 సెం.మీ మరియు ∠ACB = 30° అయిన BC మరియు AC భుజాల పొడవులను కనుగొనండి. (పేజీ నెం. 282),
సాదన.
∠ACB = 30° మరియు AB = 5 సెం.మీ అని ఇవ్వబడింది. BC భుజం పొడవును కనుగొనాలంటే కోణం C పరంగా AB మరియు BC కి సంబంధించిన
త్రికోణమితీయ నిష్పత్తిని తీసుకోవాలి.
కోణం C కు BC కి సంబంధించిన త్రికోణమితీయ. నిష్పత్తిని తీసుకోవాలి. కోణం C కు BC అనేది ఆసన్న భుజం మరియు AB అనేది ఎదుటి భుజం అవుతాయి.
కావున \(\frac{\mathrm{AB}}{\mathrm{BC}}\) = tan c
i.e., \(\frac{5}{B C}\) = tan 30 = \(\frac{1}{\sqrt{3}}\)

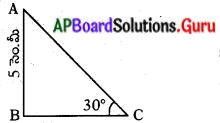
ఈ విధంగా BC = 5√3 సెం.మీ.
AC² = AB² + BC² (పైథాగరస్ సిద్ధాంతం ప్రకారం)
AC² = 5² + (5√3)²
AC² = 25 + 75
AC = √100 = 10 సెం.మీ.

ప్రశ్న 5.
6 సెం.మీ. వ్యాసార్ధం కలిగిన వృత్తంలో ఒక జ్యా కేంద్రం వద్ద 60° కోణం చేస్తుంది. ఆ జ్యా పొడవును కనుగొనండి. (పేజీ నెం. 283)
సాధన.
OA = OB = 6 సెం.మీ. వ్యాసార్ధం
∠AOB = 60° ఇవ్వబడినది
AB పైకి ‘O’ నుండి OC ఎత్తు గీయబడింది అనుకొనుము.

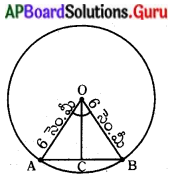
∠COB = 30°
∆COB లో
sin 30° = \(\frac{\mathrm{BC}}{\mathrm{OB}}\)
\(\frac{1}{2}=\frac{B C}{6}\)
BC = \(\frac{6}{2}\)
కాని, జ్యా పొడవు AB = 2BC = 2 × 3 = 6 సెం.మీ.
∴ జ్యా పొడవు = 6 సెం.మీ.

ప్రశ్న 6.
Qవద్ద లంబకోణం ఉన్న ∆PQRలో PQ = 3 సెం.మీ. మరియు PR = 6 సెం.మీ. అయిన ∠QPR మరియు ∠PRQ. (పేజీ నెం. 284)
సాధన.

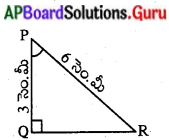
PQ = 3 సెం.మీ మరియు PR = 6 సెం.మీ.
\(\frac{P Q}{P R}\) = sin R
∴ ∠PRQ = 30°
ఇంకా, ∠QPR = 60°

ప్రశ్న 7.
sin (A – B) = \(\frac{1}{2}\), cos (A + B) = \(\frac{1}{2}\), 0° < A + B ≤ 90°, A > Bఅయిన A మరియు B విలువలు కనుక్కోండి. (పేజీ నెం. 284)
సాధన.
sin (A – B) = \(\frac{1}{2}\), A – B = 30°
ఇంకా, Cos (A + B) = \(\frac{1}{2}\),
A + B = 60°
పై రెండు సమీకరణాల నుండి : A = 45° మరియు B = 15°.

ప్రశ్న 8.
\(\frac{\sec 35^{\circ}}{\operatorname{cosec} 55^{\circ}}\) ను గణించుము. (పేజీ నెం. 287)
సాధన.
cosec A = sec (90°- A)
cosec 55° = sec (90° – 35°)
cosec 55° = sec 35°
ఇక \(\frac{\sec 35^{\circ}}{\operatorname{cosec} 55^{\circ}}=\frac{\sec 35^{\circ}}{\sec 35^{\circ}}\) = 1

ప్రశ్న 9.
cos 7A = sin (A – 6°) ఇంకా అల్పకోణం అయిన A విలువ ఎంత ? (పేజీ నెం. 287)
సాధన.
cos 7A = sin(A – 6°) అని ఇవ్వబడింది…. (1)
sin (90 – 7A) = sin (A – 6°)
7A లఘుకోణం కావున (90° – 7A) మరియు (A – 6°) లు కూడా లఘుకోణాలవుతాయి.
90° – 7A = A – 6°
8A = 96°
∴ A = 12°.

ప్రశ్న 10.
sin A = cos B అయిన A + B = 90° అని చూపుము. (పేజీ నెం. 287)
సాధన.
sin A = cos B అని ఇవ్వబడింది ………….. (1)
cos B = sin (90° – B) అని తెలుసు.
కావున sin A = sin (90° – B)
A, B లు లఘుకోణాలు అయిన A = 90° – B
⇒ A + B = 90°.

ప్రశ్న 11.
sin 81° + tan 81° విలువను 0° మరియు 45° మధ్య త్రికోణమితీయ నిష్పత్తులలో చూపుము. (పేజీ నెం. 287)
సాధన.
sin 81° = sin (90° – 9°) = cos 9°
tan 81° = tan(90° – 9°) = cot 9°
∴ sin 81° + tan 81° = cos 9° + cot 9°

ప్రశ్న 12.
త్రిభుజం ABC లోని అంతర కోణాలు A, B మరియు Cలు అయిన sin B+ C = cos A అని నిరూపించండి. (పేజీ నెం. 288)
సాధన.
A, B మరియు C లు ∆ABC లోని కోణాలు కావున
A + B + C = 180°
ఇరువైపులా 2చే భాగించగా
\(\frac{A}{2}+\frac{B+C}{2}\) = 90°
\(\frac{\mathrm{B}+\mathrm{C}}{2}\) = 90° – \(\frac{A}{2}\)
ఇరువైపులా త్రికోణమితీయ నిష్పత్తి sin తీసుకొనగా
sin (\(\frac{\mathrm{B}+\mathrm{C}}{2}\)) = sin (90° – \(\frac{A}{2}\))
sin (\(\frac{\mathrm{B}+\mathrm{C}}{2}\)) = cos \(\frac{A}{2}\)

ప్రశ్న 13.
cot θ + tan θ = sec θ cosec θ నిరూపించండి. (పేజీ నెం. 290)
సాధన.
L.H.S. = cot θ + tan θ
= \(\frac{\cos \theta}{\sin \theta}+\frac{\sin \theta}{\cos \theta}\)
= \(\frac{\cos ^{2} \theta+\sin ^{2} \theta}{\sin \theta \cos \theta}\)
= \(\frac{1}{\sin \theta \cos \theta}\)
= \(\frac{1}{\sin \theta} \cdot \frac{1}{\cos \theta}\)
= cosec θ sec θ

ప్రశ్న 14.
tan² θ + tan⁴ θ = sec⁴ θ – sec² θ (పేజీ నెం. 291)
సాధన.
L.H.S. = tan² θ + tan⁴ θ
= tan² θ (1 + tan² θ)
= tan² θ. sec² θ
= (sec² θ – 1) sec² θ
= sec⁴ θ – sec² θ = R.H.S.

ప్రశ్న 15.
\(\sqrt{\frac{1+\cos \theta}{1-\cos \theta}}\) = cosec θ + cot θ (పేజీ నెం. 291)
సాధన.