SCERT AP 10th Class Maths Textbook Solutions Chapter 12 త్రికోణమితి అనువర్తనాలు Exercise 12.1 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 12th Lesson త్రికోణమితి అనువర్తనాలు Exercise 12.1
ప్రశ్న 1.
భూమిపై ఒక టవర్ నిటారుగా నిలిచి ఉంది. ఆ టవర్ అడుగు నుండి 15 మీటర్ల దూరం నుండి ఆ టవర్ పై కొన 45° ఊర్ధ్వకోణంలో పరిశీలించబడింది. ఆ టవర్ ఎత్తు ఎంత ?
సాధన.
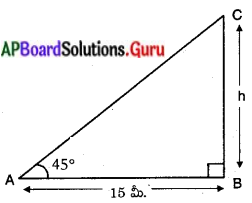
పటంలో ‘A’ పరిశీలన బిందువు.
AB అనునది పరిశీలన బిందువు నుండి టవర్ యొక్క అడుగుకు గల దూరము = 15 మీ.
BC అనునది టవర్ ఎత్తు ‘h’ అనుకొనుము.
ఊర్థ్వకోణము = ∠CAB = 45°
∆ABC లో
tan 45° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ 1 = \(\frac{h}{15}\)
⇒ h = 15 మీ.
టవర్ ఎత్తు (h) = 15 మీ.
![]()
ప్రశ్న 2.
ఒక చెట్టు గాలికి విరిగి, విరిగిన పై భాగం భూమికి 300 ల కోణం చేస్తూ భూమిపై పడింది. చెట్టు అడుగుభాగం నుండి, కిందపడిన చెట్టుకొన మధ్య దూరం 6 మీటర్లు. చెట్టు విరగక ముందు ఆ చెట్టు ఎత్తు ఎంత ?
సాధన.
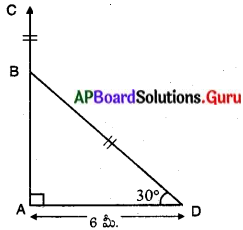
పటంలో, AC = చెట్టు అసలు ఎత్తు.
గాలి వీయడం వలన చెట్టు “B” వద్ద విరిగి, విరిగిన భాగము 30° కోణంతో D ను తాకెను.
AD = 6 మీ.
∆BAD లో,
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{AD}}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{\mathrm{AB}}{6}\)
⇒ AB = \(\frac{6}{\sqrt{3}}\) మీ.
∆BAD లో, cos 30° = \(\frac{\mathrm{AD}}{\mathrm{BD}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{6}{B D}\)
⇒ BD = \(\frac{12}{\sqrt{3}}\)
∴ AC = AB + BC = AB + BD (::: BC = BD)
= \(\frac{6}{\sqrt{3}}+\frac{12}{\sqrt{3}}=\frac{18}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\) = 6√3 మీ.
![]()
ప్రశ్న 3.
ఒక పా లో పిల్లలు ఆడుకోవడానికి ఒక కాంట్రాక్టర్ ఒక జారుడు బల్లను ఏర్పాటు చేయాలనుకున్నారు. దానిని 2 మీటర్ల ఎత్తుతో, భూమితో 300 ల కోణం చేసేటట్లు ఏర్పరచాలనుకుంటే ఆ జారుడు బల్ల పొడవు ఎంత ఉంటుంది ?
సాధన.
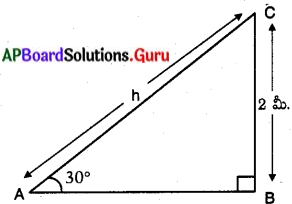
పటంలో, ‘A’ భూమిపై పరిశీలన బిందువు అనుకొనుము.
‘C’ బల్లను ఏర్పాటు చేయు స్థానము.
A జారుడు బల్ల ఎత్తు = 2 మీ.
ఊర్థ్వకోణము = 30°
∆ABC లో sin 30° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
\(\frac{1}{2}=\frac{2}{h}\)
h = 4 మీ.
∴ జారుడు బల్ల పొడవు = 4 మీ.
![]()
ప్రశ్న 4.
ఉదయం 7 గంటలకు 15 మీటర్ల ఎత్తు గల స్థంభం యొక్క నీడ పొడవు 5√3 మీటర్లు. ఆ సమయంలో సూర్యకిరణాలు, భూమితో ఎంత కోణం చేస్తున్నాయి?
సాధన.
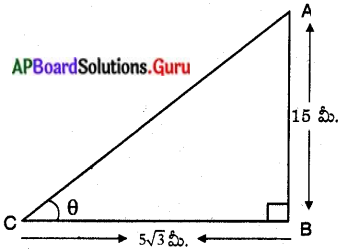
పటంలో, AB = స్థంభం అసలు ఎత్తు = 15 మీ.
BC = స్థంభం యొక్క నీడ పొ .కవు = 5/3 మీ.,
‘B’ అనునది ఆ సమయంలో సూర్యకిరణాలు,
భూమితో చేయు కోణం అనుకొనుము. లంబకోణ త్రిభుజం ∆ABC నుండి,
tan θ = \(\frac{A B}{B C}\)
⇒ tane = \(\frac{15}{5 \sqrt{3}}\)
⇒ tane = \(\frac{3}{\sqrt{3}}=\frac{3 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}}=\frac{3 \sqrt{3}}{3}\) = √3
⇒ tan θ = √3
⇒ tan θ = tan 60°
⇒ θ = 60°
∴ ఆ సమయంలో సూర్య కిరణాలు, భూమితో చేయు కోణము 60°.
![]()
ప్రశ్న 5.
పవన్ 10 మీటర్ల ఎత్తు గల స్తంభాన్ని 3 బలమైన తాళ్ళ సహాయంతో నిలబెట్టాలనుకున్నాడు. ఒక్కొక్క త్రాడు స్తంభంతో 30° కోణం చేయాల్సి ఉంటే ఎంత పొడవు తాడు తీసుకోవాలి ?
సాధన.
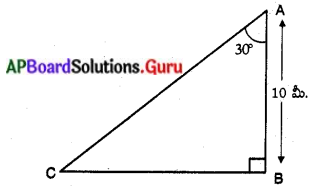
పటంలో, AB = స్తంభము యొక్క ఎత్తు = 10 మీ.
AC = త్రాడు యొక్క పొడవు.
త్రాడు, స్తంభంతో చేయు కోణము = 30°
∆ABC లో, cos 30° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{10}{\mathrm{AC}}\)
⇒ AC = \(\frac{2 \times 10}{\sqrt{3}}\)
= \(\frac{20}{\sqrt{3}}=\frac{20}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{20 \sqrt{3}}{3}\)
కావలసిన తాడు పొడవు = 3 × \(\frac{20 \sqrt{3}}{3}\) = 20√3 మీ.
![]()
ప్రశ్న 6.
విజయ్ భూమి నుండి 6 మీటర్ల ఎత్తు గల భవనంపై నుండి భూమిపై నున్న ఒక లక్ష్యాన్ని 60° నిమ్న కోణంలో బాణంతో ఛేదించాలనుకున్నాడు. విజయ్ నుండి లక్ష్యం ఎంత దూరంలో ఉంటుంది ?
సాధన.
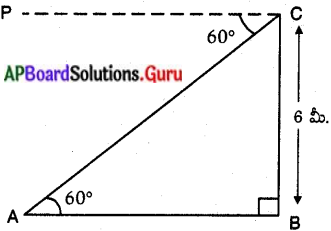
పటంలో, BC = భవనం ఎత్తు = 6 మీ.
‘C’ పరిశీలన బిందువు మరియు A భూమిపై గల లక్ష్యం యొక్క స్థానము.
నిమ్నకోణము = ∠CAB = 60°
AB = భూమిపై గల లక్ష్యంకు, భవనంకు మధ్య గల దూరము.
∆ABC లో,
sin 60° = \(\frac{\mathrm{BC}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{6}{A C}\)
⇒ AC = \(\frac{12}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{12 \sqrt{3}}{3}\) = 4√3 మీ. –
∴ విజయ్ నుండి లక్ష్యంకు గల దూరము AC = 4√3 మీ.
![]()
ప్రశ్న 7.
9 మీటర్ల ఎత్తు గల విద్యుత్ స్తంభంపై ఒక ఎలక్టీషియన్ మరమ్మత్తు పనిచేయాల్సి ఉంది. మరమ్మత్తు చేయడానికి ఆ స్తంభం పై నుండి 1.8 మీటర్ల తక్కువ ఎత్తుకు చేరాలి. ఒక నిచ్చెనను భూమిపై 60° కోణంతో పెట్టాల్సి వస్తే ఎంత పొడవు గల నిచ్చెనను తీసుకోవాలి ? నిచ్చెన అడుగుభాగం నుండి స్తంభం అడుగుభాగం దూరం ఎంత ?
సాధన.
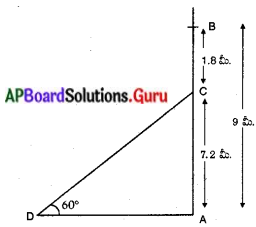
పటంలో, AB = విద్యుత్ స్తంభం ఎత్తు = 9 మీ.
AC = కావలసిన అసలు స్తంభం ఎత్తు = 7.2 మీ.
ఊర్ధ్వకోణము = ∠CDA = 60°
CD = నిచ్చెన పొడవు
AD = నిచ్చెన అడుగు భాగం నుండి స్తంభం అడుగు భాగంకు గల దూరము.
sin 60° = \(\frac{\mathrm{AC}}{\mathrm{DC}}\)
\(\frac{\sqrt{3}}{2}=\frac{7.2}{\mathrm{DC}}\)
∴ DC = 7.2 × \(\frac{2}{\sqrt{3}}\)
∆ADC లో,
= 7.2 × \(\frac{2}{\sqrt{3}}\) × \(\frac{\sqrt{3}}{\sqrt{3}}\)
= 7.2 × \(\frac{2 \sqrt{3}}{3}\)
నిచ్చెన పొడవు DC = 8.3136 మీ.
∆ADC లో,
⇒ tan 60° = \(\frac{\mathrm{AC}}{\mathrm{DC}}\)
⇒ √3 = \(\frac{7.2}{D C}\)
⇒ AD = \(\frac{7.2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\) = 2.4√3
= 4.1568 మీ.
∴ నిచ్చెన అడుగు భాగం నుండి స్తంభం అడుగు భాగంకు గల దూరము = 4.1568 మీ.
![]()
ప్రశ్న 8.
ఒక నావ ఒక నదిని దాటాల్సి ఉంది. నదీ ప్రవాహం కారణంగా ఆ నదీ తీరంతో 60°ల కోణం చేస్తున్న ఆ నావ 600 మీటర్లు ప్రయాణించి అవతలి తీరాన్ని చేరింది. ఆ నది వెడల్సెంత ?
సాధన.
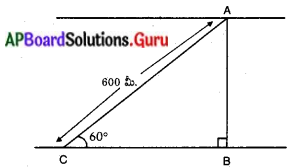
పటంలో, ‘A’ నావ వేరొక వైపుకు చేరవలసిన స్థానము.
‘C’ ప్రస్తుతము నావ ఉన్న స్థానము (లేక) పరిశీలన స్థానము.
AC = నావ ప్రయాణించిన దూరము = 600 మీ.
ఊర్ధ్వకోణము = ∠ACB = 60°
AB = నది అసలు వెడల్పు అనుకొనుము.
లంబకోణ త్రిభుజము ABC లో sin 60° = \(\frac{\mathrm{AB}}{\mathrm{AC}}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{\mathrm{AB}}{600}\)
⇒ AB = 600 × \(\frac{\sqrt{3}}{2}\)
⇒ AB = 300√3 మీ.
∴ నది వెడల్పు = 300√3 మీ.
ప్రశ్న 9.
1.8 మీ. ఎత్తు ఉన్న ఒక పరిశీలకుడు ఒక తాటి చెట్టు నుండి 13.2 మీటర్ల దూరంలో ఉన్నాడు. ఆ చెట్టుపై పరిశీలకుడి కంటి నుండి 45° ఊర్ధ్వకోణం చేస్తుంది. ఆ చెట్టు ఎత్తు ఎంత ?
సాధన.
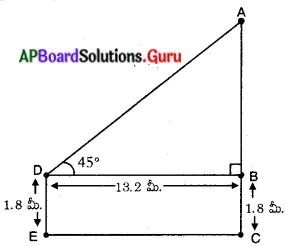
పటంలో, DE = పరిశీలకుని ఎత్తు = 1.8 మీ.
AC = తాటి చెట్టు ఎత్తు.
‘D’ = పరిశీలన బిందువు.
BD = తాటి చెట్టు నుండి పరిశీలకునికి మధ్యన గల దూరము = 13.2 మీ.
ఊర్థ్వకోణము ∠ADB = 45° అనుకొనుము. మరియు DE = BC = 1.8 మీ.
లంబకోణ త్రిభుజము ABD లో,
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ 1 = \(\frac{\mathrm{AB}}{13.2}\)
⇒ AB = 13.2 మీ.
AC = AB + BC = 13.2 + 1.8 = 15.0 మీ.
∴ తాటి చెట్టు ఎత్తు (AC) = 15 మీ.
ప్రశ్న 10.
క్రిందనున్న పటంలో AC = 6 సెం.మీ. AB = 5 సెం.మీ. మరియు BAC = 300 అయిన త్రిభుజ వైశాల్యాన్ని కనుగొనుము.
సాధన.
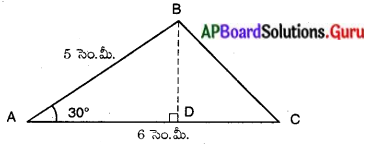
ఇచ్చిన పటంలో BD ⊥ AC అవునట్లు BD ని గీద్దాము.
∆ADB లో ∠A = 30°
∴ sin 30° = \(\frac{\mathrm{BD}}{\mathrm{AB}}\)
⇒ \(\frac{1}{2}=\frac{B D}{5}\)
2BD = 5
⇒ BD = \(\frac{5}{2}\)
ABC త్రిభుజ వైశాల్యం \(\frac{1}{2}\) bh = \(\frac{1}{2}\) AC × BD
= \(\frac{1}{2}\) × 6 × \(\frac{5}{2}\)
= \(\frac{15}{2}\) చు/సెం.మీ.