AP Board 10th Class Maths Solutions Chapter 12 త్రికోణమితి అనువర్తనాలు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 12 త్రికోణమితి అనువర్తనాలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 12th Lesson త్రికోణమితి అనువర్తనాలు InText Questions

ఇది చేయండి:

ప్రశ్న 1.
కింది సందర్భాలకు పటాలను గీయండి. (పేజీ నెం. 297)
(i) ఒక వ్యక్తి ‘a’ ఊర్థ్వ కోణముతో ఒక గాలిపటాన్ని ఎగురవేస్తున్నాడు. గాలిపటాన్ని ‘1’ పొడవు గల దారంతో ఎగురవేస్తున్నాడు. ఈ సందర్భానికి పటాన్ని గీయండి.
(ii) ఒక నది యొక్క ఒక వైపు ఉన్న ‘h’ ఎత్తుగల చెట్టుపై నుండి నది యొక్క రెండు తీరాలను θ₁ మరియు θ₂ (θ₁ < θ₂) నిమ్న కోణాలతో ఒక వ్యక్తి పరిశీలించాడు. నది వెడల్పు ‘d’ అయిన ఈ సందర్భానికి పటాన్ని గీయండి.
సాధన.
(i)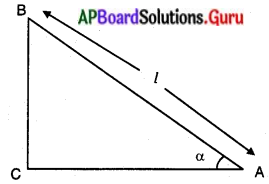

పై పటంలో
A పరిశీలకుని స్థానము
B గాలిపటము యొక్క స్థానము
AB అనునది ‘l’ పొడవు గల దారము.

(ii)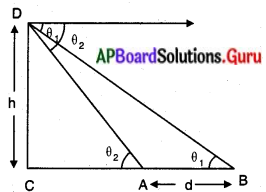

పటంలో
‘D’ పరిశీలకుని స్థానము
CD చెట్టు యొక్క ఎత్తు
AB నది వెడల్పు
θ₁ మరియు θ₂ లు నిమ్న కోణాలు.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
మీ పాఠశాల భవనం నుండి ‘d’ దూరంలో గల బిందువు నుండి భవనం పై భాగాన్ని ‘a’ ఊర్థ్వ కోణముతో పరిశీలించారు. ఈ పాఠశాల భవనం ఎత్తును కనుగొనడానికి ఏ త్రికోణమితీయ నిష్పత్తిని ఎంచుకొంటారు ? (పేజీ నెం. 297)
సాధన.

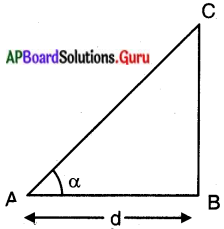
పటమును అనుసరించి, ఆసన్న భుజము మరియు ఊర్థ్వకోణములను బట్టి tan α గాని cot α గాని ఎంచుకొంటాను.

ప్రశ్న 2.
‘x’ మీటర్ల పొడవు గల ఒక నిచ్చెన భూమితో ఆ కోణం చేస్తూ ఒక గోడకు వేయబడి ఉంది. నిచ్చెన పై భాగం స్పృశించిన గోడ స్థానం యొక్క ఎత్తును కనుక్కోవడానికి ఏ త్రికోణమితీయ నిష్పత్తిని ఎంచుకోవాలి ? (పేజీ నెం. 297)
సాధన.

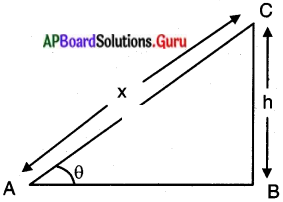
∆ABC లో B కు ఎదుటి భుజమును కనుగొనాలి. ఊర్థ్వకోణము, కర్ణముల విలువలు మనకు తెలియును కావున sin θ గాని cosec θ గాని ఎంచుకొంటాను.

ఉదాహరణలు:

ప్రశ్న 1.
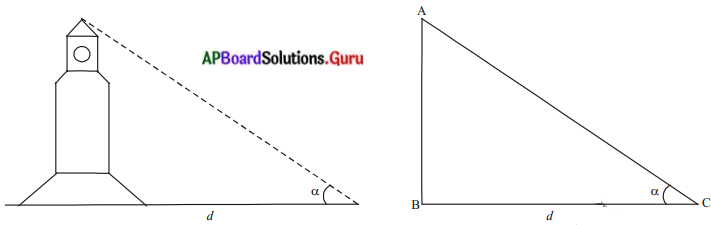
పరిశీలకుని నుండి d మీటర్ల దూరంలో నున్న ఒక క్లాక్ టవర్ యొక్క పై కొన C° ఊర్ధ్వకోణం చేస్తుంది. ఈ సందర్భానికి తగిన పటాన్ని గీయండి. (పేజీ నెం. 295)
సాధన.
సమస్య ఆధారంగా ఈ క్రింది పటం గీయవచ్చు.

ప్రశ్న 2.
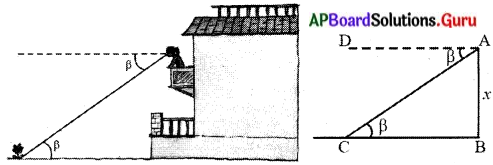
రింకి మొదటి అంతస్థులోని బాల్కనీ నుండి బయటి భూమిపై నున్న పూవును P° నిమ్నకోణంతో చూస్తుంది. మొదటి – అంతస్థు ఎత్తు X మీటర్లు. ఈ సందర్భానికి తగిన పటాన్ని గీయండి. (పేజీ నెం. 296)
సాధన.
ఇక్కడ ∠DAC = ∠ACB = β

ప్రశ్న 3.
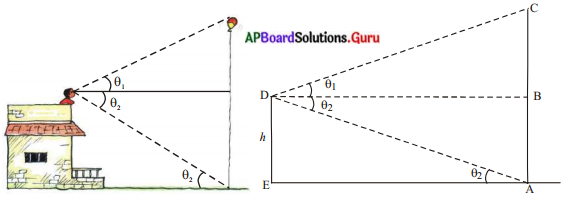
ఒక పెద్ద త్రాడు సహాయంతో ఒక పెద్ద బెలూన్ గాలిలో తేలుతుంది. ఒక భవనంపై నున్న ఒక వ్యక్తి దాని పై భాగాన్ని θ₁ ఊర్ధ్వకోణంతో మరియు త్రాడు అడుగు భాగాన్ని θ₂ నిమ్నకోణంతో పరిశీలించాడు. ఆ భవనం ఎత్తు + అడుగులు. – ఈ సందర్భానికి తగిన పటాన్ని గీయండి. (పేజీ నెం. 296)
సాధన.
ఇక్కడ మనం గమనించగా,
∠BDA = ∠DAE

ప్రశ్న 4.
ఒక బాలుడు ఒక విద్యుత్ స్తంభం అడుగు భాగం నుండి 8 మీటర్ల దూరంలో ఉన్న బిందువు నుండి విద్యుత్ స్తంభం పై భాగాన్ని 60° ఊర్థ్వకోణాలతో పరిశీలించాడు. ఆ స్తంభం ఎత్తును కనుక్కోండి. (పేజీ నెం. 297)
సాధన.

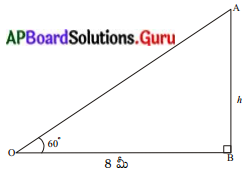
పటం నుండి, త్రిభుజం OAB నుండి
OB = 8 మీటర్లు ∠AOB = 60°
స్తంభం ఎత్తు = AB = h మీటర్లు అనుకొనగా, (∆DAB లో ∠AOB యొక్క ఆసన్న భుజం విలువ మనకు తెలుసు. మనం “ఎదుటి భుజం” విలువను కనుక్కోవాలి. కావున ఆసన్న భుజం మరియు ఎదుటి భుజాల నిష్పత్తి “tan” ను పరిగణించాలి). ”
tan 60° = \(\frac{A B}{O B}\)
√3 = \(\frac{h}{8}\) మీ.
∴ h = 8√3 మీ.

ప్రశ్న 5.
ఒక హెలికాప్టర్ లో ఉన్న రాజేందర్ భూమిపై ఉన్న ఒక వ్యక్తిని 45° నిమ్నకోణంతో పరిశీలించాడు. భూమిపై నుండి హెలీకాప్టర్ 50 మీటర్ల ఎత్తులో ఎగురుతూ ఉంటే, రాజేందర్‌కు, ఆ వ్యక్తి ఎంత దూరంలో ఉన్నాడు ? (పేజీ నెం. 298)
సాధన.

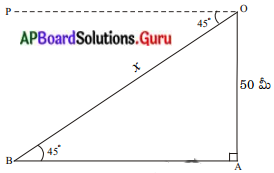
పటం నుండి, త్రిభుజం OAB లో
OA = 50 మీటర్లు
∠POB = ∠OBA = 45°
OB = రాజేందర్ నుండి వ్యక్తి దూరం = x.
(త్రిభుజం OAB లో ∠OBA యొక్క 150 మీ. ఎదుటి భుజం కొలత మనకు తెలుసు. కర్ణం OB విలువ కనుక్కోవాలి. ఎదుటి భుజం కర్ణాల నిష్పత్తి “sin” కావున “sin” ను ఎంచుకొంటాం)
sin 45° = \(\frac{\mathrm{OA}}{\mathrm{OB}}\)
\(\frac{1}{\sqrt{2}}=\frac{50}{x}\)
∴ x = 50√2 మీటర్లు
రాజేందర్ నుండి 50√2 మీటర్ల దూరంలో వ్యక్తి ఉన్నాడు.

ప్రశ్న 6.
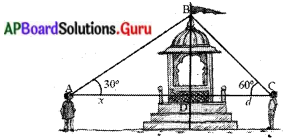
30 మీటర్ల ఎత్తు గల ఒక గుడి పై భాగాన్ని, దాని ఇరువైపులా నున్న ఇద్దరు వ్యక్తులు 30° మరియ 60° ఊర్థ్వకోణాలలో పరిశీలించారు. ఆ ఇద్దరు వ్యక్తుల మధ్య దూరం ఎంత ? (పేజీ నెం. 301)
సాధన.
పటము నుండి దేవాలయం ఎత్తు BD = 30 మీటర్లు
మొదటి వ్యక్తి పరిశీలిస్తున్నపుడు ఊర్ధ్వకోణం ∠BAD = 30°
రెండవ వ్యక్తి పరిశీలిస్తున్నపుడు ఊర్ధ్వకోణం ∠BCD = 60°
మొదటి వ్యక్తి నుండి గుడి దూరం AD = x,
రెండవ వ్యక్తి నుండి గుడి దూరం CD = d అనుకొనగా

∆BAD నుండి

tan 30° = \(\frac{\mathrm{BD}}{\mathrm{AD}}\)
\(\frac{1}{\sqrt{3}}=\frac{30}{x}\)
x = 30√3 ………….. (1)

∆BCD నుండి
tan 60° = \(\frac{\mathrm{BD}}{\mathrm{AD}}\)
√3 = \(\frac{30}{\mathrm{~d}}\)
d = \(\frac{30}{\sqrt{3}}\) …………… (2)

(1) మరియు (2) ల నుండి ఇద్దరు వ్యక్తుల మధ్య దూరం = AD + DC = x + d
= 30√3 + \(\frac{30}{\sqrt{3}}\)
= \(\frac{90+30}{\sqrt{3}}=\frac{120}{\sqrt{3}}\)
= 40√3 మీటర్లు.

ప్రశ్న 7.
ఒక టవర్ పాదం వరకు ఒక చక్కని (straight) రహదారి ఉంది. ఆ టవర్ పై నిలబడి ఉన్న రామయ్య అనే వ్యక్తి దూరం నుండి వస్తున్న కారును 30°ల నిమ్నకోణంలో చూశాడు. సమవేగంతో వస్తున్న ఆ కారును 6 సెకండ్ల తర్వాత 600 నిమ్నకోణంలో గమనించాడు. ఈ స్థానం నుండి కారు టవర్‌ను చేరడానికి పట్టు కాలం ఎంత ? (పేజీ నెం. 301)
సాధన.
పటం నుండి,
6 సెకండ్లలో కారు ప్రయాణించిన దూరం = AB = x మీటర్లు
టవర్ ఎత్తు CD = h మీటర్లు
కారు ప్రయాణించాల్సిన మిగిలిన దూరం BC = d మీటర్లు
AC = AB + BC = (x + d) మీటర్లు
∠PDA = ∠DAC = 30°
∠PDB = ∠DBC = 60°

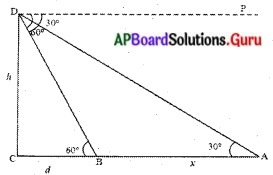
∆BCD నుండి,
tan 60° = \(\frac{\mathrm{CD}}{\mathrm{BC}}\)
√3 = \(\frac{\mathrm{h}}{\mathrm{d}}\)
⇒ h = √3d ………. (1)

∆ACD నుండి,
tan 30° = \(\frac{\mathrm{CD}}{\mathrm{AC}}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{(x+d)}\)
⇒ h = \(\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}\) …………… (2)
(1) మరియు (2)ల నుండి,
\(\frac{(\mathrm{x}+\mathrm{d})}{\sqrt{3}}\) = √3d
x + d = 3d
x = 2d
⇒ d = \(\frac{x}{2}\)
‘x’ మీటర్ల దూరం ప్రయాణించడానికి పట్టు కాలం = 6 సెకండ్లు
‘d’ = \(\frac{x}{2}\) మీటర్ల దూరం ప్రయాణించడానికి పట్టు కాలం = 3 సెకండ్లు.