AP Board 10th Class Maths Solutions Chapter 13 సంభావ్యత Exercise 13.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 13 సంభావ్యత Exercise 13.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 13th Lesson సంభావ్యత Exercise 13.2

ప్రశ్న 1.
ఒక సంచిలో 3 ఎరుపు, 5 నలుపు బంతులు కలవు. సంచి నుంచి యాదృచ్ఛికంగా ఒక బంతిని తీస్తే అది
(i) ఎరుపుదై ఉండుటకు
(ii) ఎరుపుది కాకపోవుటకు సంభావ్యతలు ఎంతెంత?
సాధన.
(i) సంచిలోని మొత్తం బంతుల సంఖ్య = 3 ఎరుపు + 5 నలుపు = 8 బంతులు
ఎరుపు బంతి అగుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 3
ఎరుపు బంతి పొందుటకు గల సంభావ్యత .
P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{3}{8}\)

(ii) P(\(\overline{\mathrm{E}}\)) అనునది పరస్పర ఘటన అయిన
⇒ P(E) + P(\(\overline{\mathrm{E}}\)) = 1
P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
P (E) = 1 – \(\frac{3}{8}\)
= \(\frac{5}{8}\).
∴ బంతి ఎరుపుది కాకపోవుటకు సంభావ్యత = \(\frac{5}{8}\).

ప్రశ్న 2.
ఒక పెట్టెలో 5 ఎరుపు, 8 తెలుపు, 4 ఆకుపచ్చ గోళీలు కలవు. పెట్టె నుండి యాదృచ్ఛికంగా ఒక గోళీను తీస్తే అది
(i) ఎరుపు
(ii) తెలుపు
(iii) ఆకుపచ్చకానిది అగుటకు – సంభావ్యతలు కనుగొనండి.
సాధన.
పెట్టెలోని మొత్తం గోళీల సంఖ్య = 5 ఎరుపు + 8 తెలుపు + 4 ఆకుపచ్చ
= 5 + 8 + 4 = 17

(i) ఎరుపు, గోళీల సంఖ్య = 5
ఎరుపు గోళీని పొందుటకు అనుకూల పర్యవసానాల సంఖ్య = 5
ఎరుపు గోళీల సంభావ్యత P(R) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
∴ P(R) = \(\frac{5}{17}\).

(ii) తెలుపు గోళీల సంఖ్య = 8 తెలుపు గోళీ లభించు అనుకూల పర్యవసానాల సంఖ్య = 8

P (W) = అనుకూల పర్యవసానాల సంఖ్య/ మొత్తం పర్యవసానాల సంఖ్య
∴ P(W) = \(\frac{8}{17}\)

(iii) ఆకుపచ్చని కాని మిగిలిన గోళీల సంఖ్య = 5 + 8 = 13
ఆకుపచ్చవి కాని గోళీ లభించు అనుకూల పర్యవసానాల సంఖ్య = 13
P(\(\overline{\mathrm{G}}\)) = P (ఆకుపచ్చకాని గోళీలు)
= అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
∴ P (\(\overline{\mathrm{G}}\)) = \(\frac{13}{17}\)
(లేదా)
ఆకుపచ్చ గోళీల సంభావ్యత = P(G)
= ఆకుపచ్చ గోళీల సంఖ్య / మొత్తం గోళీల సంఖ్య
= \(\frac{4}{17}\)
⇒ P(G) + P(\(\overline{\mathrm{G}}\)) = 1
∴ P(\(\overline{\mathrm{G}}\)) = 1 – P(G)
= 1 – \(\frac{4}{17}\) = \(\frac{13}{17}\)

ప్రశ్న 3.
ఒక కిట్టి బ్యాంకు డబ్బాలో వంద 50పై నాణెములు, యాభై ₹ 1 నాణెములు, ఇరవై ₹ 2 నాణెములు, పది ₹ 5 నాణెములు ఉన్నాయి. డబ్బాను తలక్రిందులు చేసినప్పుడల్లా యాదృచ్ఛికంగా ఒక్క నాణెం పడుతుంటే అది
(i) 50 పై నాణెం అగుటకు,
(ii) ₹ 5 నాణెం ‘కాకపోవుటకు సంభావ్యతలు ఎంతెంత?
సాధన.
(i)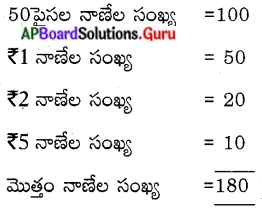
∴ మొత్తం అనుకూల పర్యవసానాల సంఖ్య = 180
50 పైసల నాణెం పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 100
50 పైసల నాణెం పొందుటకు సంభావ్యత

P (E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{100}{180}=\frac{5}{9}\)

(ii) P(E) అనునది ₹ 5 యందు సంభావ్యత అనుకొనిన ₹ 5 నాణెం పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 10
∴ ₹ 5 పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{10}{180}=\frac{1}{18}\)
కానీ, P(\(\overline{\mathrm{E}}\)) ₹ 5 నాణెం కాకపోవుటకు గల సంభావ్యత అనుకొనుము.
P(E) + P(\(\overline{\mathrm{E}}\)) = 1
∴ P((\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{1}{18}\)
∴ ₹ 5 నాణెం కాకపోవుటకు సంభావ్యత = \(\frac{17}{18}\).

ప్రశ్న 4.
గోపి అక్వేరియం నుండి ఒక చేపను కొన్నాడు అక్వేరియంలో 5 మగ చేపలు, 8 ఆడ చేపలు ఉండినప్పుడు, వ్యాపారి యాదృచ్ఛికముగా ఒక చేపను తీసి ఇచ్చి ఉంటే, ఆ చేప మగ చేప అవడానికి సంభావ్యత ఎంత?

సాధన.
మగ చేపల సంఖ్య = 5
ఆడ చేపల సంఖ్య = 8
మొత్తం చేపల సంఖ్య = 5 మగ + 8 ఆడ = 13 చేపలు
ఒక చేపను బయటకు యాదృచ్ఛికంగా తీయుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 13
మొత్తం మగ చేపల సంఖ్య = 5 అయిన
మగ చేపను పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 5
మగ చేపను పొందుటకు గల సంభావ్యత P (E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
∴ P (E) = \(\frac{5}{13}\).

ప్రశ్న 5.
ఒక ఆట నందు వేగంగా త్రిప్పబడిన బాణపు గుర్తు పటములో చూపబడినట్లు, 1, 2, 3, 4,5, 6, 7 లేక 8 ని సూచిస్తూ ఆగుతుంది. అన్ని పర్యవసానములు సమసంభవములైతే క్రింది ఘటనల సంభావ్యతలు లెక్కించండి. బాణపు గుర్తు సూచించేది.
(i) 8
(ii) ఒక బేసిసంఖ్య
(iii) 2 కన్నా పెద్ద సంఖ్య
(iv) 9 కన్నా చిన్న సంఖ్య.

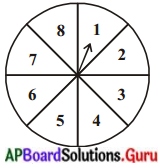
సాధన.
మొత్తం పర్యవసానాల సంఖ్య = {1, 2, …, 8} = 8
(i) ‘8’ సంఖ్యకు గల అనుకూల పర్యవసానాల సంఖ్య = 1
∴ P(8) = \(\frac{1}{8}\)

(ii)
త్రిప్పబడిన బాణపు గుర్తులో “బేసిసంఖ్య” లభించగల అనుకూల పర్యవసానాల సంఖ్య = {1, 3, 5, 7} = 4
∴ P(బేసిసంఖ్య) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{4}{8}=\frac{1}{2}\)

(iii) ‘2’ కంటే పెద్దదైన సంఖ్యను పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = {3, 4, 5, 6, 7, 8} = 6
∴ P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{6}{8}=\frac{3}{4}\) = 1.

(iv) 9 కంటే తక్కువ గల సంఖ్యను పొందగల అనుకూల పర్యవసానాల సంఖ్య = 8 {1, 2, 3, 4, 5, 6, 7, 8}
∴ P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{8}{8}\) = 1
(లేదా)
9 కంటే తక్కువ గల సంఖ్యను పొందు ఘటన ఒక కచ్ఛిత ఘటన. కనుక దీని సంభావ్యత 1.

ప్రశ్న 6.
బాగుగా కలుపబడిన పేక ముక్కల (52) కట్ట నుండి యాదృచ్ఛికంగా ఒక కార్డును తీస్తే అది క్రింది కార్డు అగుటకు సంభావ్యతలు లెక్కించండి.
(i) ఎరుపు రాజు
(ii) ముఖ కార్డు
(iii) ఎరుపు, ముఖ కార్డు
(iv) హృదయం గుర్తు గల జాకీ
(v) స్పేడ్
(vi) డైమండు గుర్తు గల రాణి
సాధన.
(i) పేక కట్ట నుండి “ఎరుపు రాజు” కార్డును తీయుటకు గల అనుకూల పర్యవసానాల సంఖ్య =
∴ ఎరుపు రాజు కార్డును పొందుటకు గల సంభావ్యత P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{2}{52}=\frac{1}{26}\)

(ii) ముఖకార్డు పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య 4 × 3 = 12 (K, Q, J)
∴ ముఖ కార్డు యాదృచ్ఛికంగా పొందు సంభావ్యత P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{12}{52}=\frac{3}{13}\)

(iii) ఎరుపు, ముఖ కార్డు గల కార్డుల సంఖ్య = 2 × 3 = 6
∴ ఎరుపు, ముఖ కార్డు పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 6
∴ ఎరుపు, ముఖ కార్డు పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{3}{26}\)

(iv) హృదయం గుర్తు గల జాకీ కార్డుల సంఖ్య =1
∴ హృదయం గుర్తు గల జాకీ కార్డుల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{52}\)

(v) స్పేడ్ కార్డుల సంఖ్య = 13
స్పేడ్ కార్డు పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 13
స్పేడ్ కార్డు పొందు సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
=\(\frac{13}{52}=\frac{1}{4}\)

(vi) డైమండ్ గుర్తు గల రాణీ కార్డుల సంఖ్య = 1
∴ డైమండ్ గుర్తు గల రాణీ కార్డు పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{52}\)

ప్రశ్న 7.
పేక ముక్కలలోని డైమండు గుర్తు గల ఐదు కార్డులు; రాజు, రాణి, జాకీ మరియు ఏ స్లను మాత్రం తీసుకొని, – బాగా కలిపి, యాదృచ్ఛికంగా ఒక కార్డును ఎన్నుకొంటే
(i) ఆ కార్డు రాణి అయ్యే సంభావ్యత ఎంత?
(ii) రాణి కార్డును తొలగించి రెండవ కార్డును ఎన్నుకొంటే అది
(ఎ) ఏస్ అగుటకు
(బి) రాణి అగుటకు సంభావ్యతలు ఎంతెంత?
సాధన.
మొత్తం కార్డుల సంఖ్య = 5
(i) రాణికార్డు అయ్యే అనుకూల పర్యవసానాల సంఖ్య =1
∴ రాణి కార్డు పొందే సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{1}{5}\)

(ii) 5 కార్డుల నుండి రాణి కార్డును తొలగించిన మిగిలిన కార్డుల సంఖ్య = 5 – 1 = 4
∴ మొత్తం పర్యవసానాల సంఖ్య = 4.
(ఎ) రాణి కార్డును తొలగించి ఏస్ కార్డును పొందగల సంభావ్యత = \(\frac{1}{4}\)

(బి) రాణి కార్డును తొలగించి మిగిలిన కార్డుల నుండి రాణి
కార్డును పొందగల సంభావ్యత = \(\frac{0}{4}\) = 0.
(∵ రాణి కార్డు పొందగల అనుకూల పర్యవసానాల సంఖ్య = 0)
∴ ఇది ఒక అసంభవ ఘటన.

ప్రశ్న 8.
లోపాలు గల 12 పెన్నులు పొరపాటుగా 132 మంచి పెన్నులలో కలసిపోయాయి. చూడగానే పెన్నులోని లోపాన్ని గుర్తించలేము. అయితే యాదృచ్ఛికంగా ఒక పెన్నును ఎన్నుకొంటే అది మంచి పెన్ను అవడానికి సంభావ్యత ఎంత?
సాధన.
మంచి పెన్నుల సంఖ్య = 132
లోపాలు గల పెన్నుల సంఖ్య = 12
∴ మొత్తం పెన్నుల సంఖ్య = 132 + 12 = 144
యాదృచ్ఛికంగా లభించగల మొత్తం పర్యవసానాల సంఖ్య = 144
144 పెన్నుల నుండి ఒక మంచి పెన్ను యాదృచ్ఛికంగా ఎంచుకొనదగు అనుకూల పర్యవసానాల సంఖ్య =132
∴ ఒక మంచి పెన్ను పొందగల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{132}{144}=\frac{11}{12}\)

ప్రశ్న 9.
20 విద్యుత్ బల్బులు కల పెట్టెలో 4 బల్బులు లోపాలు కలిగి ఉన్నవి. పెట్టె నుండి యాదృచ్ఛికంగా తీసిన బల్బు లోపాలు కలిగి ఉండుటకు సంభావ్యత ఎంత? ఒకవేళ అది మంచి బల్బు అయి ఉండి, దానిని పెట్టెలో పెట్టకుండా రెండవ బల్బును తీసుకొంటే అది కూడా మంచిదై ఉండుటకు సంభావ్యత ఎంత?
సాధన.
మొత్తం బల్బుల సంఖ్య = 20
లోపాలు గల బల్బుల సంఖ్య = 4
∴ లోపాలు లేని మంచి బల్బుల సంఖ్య = 20 – 4 = 16
∴ మొత్తం పర్యవసానాల సంఖ్య = 20.
∴ లోపాలు గల బల్బును పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 4
∴ లోపాలు గల బల్బును పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య 205
= \(\frac{4}{20}=\frac{1}{5}\)
ఒక మంచి బల్బును పెట్టె నుండి తీసి మరలా దానిలో వేయకుండా ఉంటే దానిలో గల మొత్తం బల్బుల సంఖ్య = 20 – 1 = 19.
∴ మొత్తం మంచి బల్బుల సంఖ్య = 16 – 1 = 15
∴ యాదృచ్ఛికంగా ఒక మంచి బల్బును పొందగల అనుకూల పర్యవసానాల సంఖ్య = 15
∴ రెండవసారి మంచి బల్బును పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{15}{19}\)

ప్రశ్న 10.
ఒక పెట్టెనందు 1 నుండి 90 వరకు వ్రాయబడి ఉన్న 90 ఫలకాలు ఉన్నాయి. వాటి నుండి యాదృచ్ఛికంగా ఒక ఫలకాన్ని ఎన్నుకొంటే దానిపై క్రింది సంఖ్యలు ఉండుటకు సంభావ్యత ఎంతెంత ? (i) రెండంకెల సంఖ్య
(ii) ఖచ్చిత వర్గ సంఖ్య
(iii) 5చే భాగింపబడు సంఖ్య.
సాధన.
పెట్టెలోని మొత్తం ఫలకాల సంఖ్య = 90
పెట్టెనుండి ఒక ఫలకాన్ని యాదృచ్ఛికంగా తీయుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 90
(i) పెట్టెలోని రెండంకెల సంఖ్యలు = 81 {10, 11, 12, ………… 90}
∴ రెండంకెల సంఖ్య గల ఫలకాన్ని పొందగల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{81}{90}=\frac{9}{10}\)

(ii) పెట్టెలోని ఖచ్చిత వర్గాలు గల సంఖ్యలు = 9 = {1, 4, 9, 16, 25, 36, 49, 64, 81}
∴ ఖచ్చితమైన వర్గం గల ఒక ఫలకాన్ని పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 9
∴ ఖచ్చితమైన వర్గం గల ఫలకాన్ని ఎంచుకొనుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{9}{90}=\frac{1}{10}\)

(iii) 1 నుండి 90 వరకు గల ‘5’ యొక్క గుణిజాల సంఖ్య = 18
{5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90}
అనగా 5 యొక్క గుణిజం గల ఫలకాన్ని యాదృచ్ఛికంగా పొందుటకు గల అనుకూల పర్యవసానాల సంఖ్య = 18
∴ 5 యొక్క గుణిజం గల ఫలకాన్ని పొందుటకు గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{18}{90}=\frac{1}{5}\)

ప్రశ్న 11.
పటంలో చూపినట్లు దీర్ఘచతురస్రాకార పలకపై 1మీ. వ్యాసం గల వృత్తం గీయబడి ఉన్నది. ఒక పాచికను ఈ పలకపై జారవిడిస్తే అది వృత్తంలో పడుటకు సంభావ్యత ఎంత?

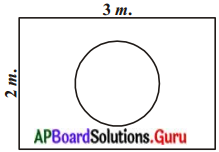
సాధన.
ఇచ్చిన దీర్ఘ చతురస్రం యొక్క పొడవు (1) = 3 మీ.
వెడల్పు (b) = 2 మీ.
దీర్ఘ చతురస్ర వైశాల్యం (A) = పొడవు × వెడల్పు
= 3 × 2 = 6 చ.మీ.
ఇచ్చిన వృత్త వ్యాసం (d) = 1 మీ.
∴ నివృత్త వైశాల్యం = nd = 2 x 141 = 1 3.
∴ దీర్ఘ చతురస్రం పై గల వృత్తం పైకి పాచికను వేయగల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{\frac{22}{28}}{6}=\frac{\cdot 22}{28 \times 6}=\frac{11}{28 \times 3}=\frac{11}{84}\)

ప్రశ్న 12.
ఒక వ్యాపారి వద్ద 144 పెన్నులు ఉన్నాయి. అందులో 20 లోపాలు కలిగి ఉన్నాయి. సుధ పెన్ను కొనడానికి వస్తే వ్యాపారి యాదృచ్ఛికంగా ఒక పెన్ను ఇస్తే దానిని
(i) సుధ కొనుటకు
(ii) కొనలేకపోవుటకు సంభావ్యతలు ఎంతెంత?
సాధన.
మొత్తం పెన్నుల సంఖ్య = 144
లోపాలు గల పెన్నుల సంఖ్య = 20
∴ మంచి పెన్నుల సంఖ్య = 144 – 20 = 124
∴ మొత్తం పర్యవసానాల సంఖ్య = 144

(i) సుధ వాటిని కొనవలెనన్న అవి మంచివి/లోపాలు లేనివి అయి ఉండాలి.
∴ సుధ పెన్ను కొనుటకు అనుకూల పర్యవసానాల సంఖ్య = 124.
∴ సుధ పెన్ను కొనుటకు కొనగల సంభావ్యత P(E) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{124}{144}=\frac{31}{36}\)

(ii) అవి లోపాలు గల పెన్నులైనట్లయితే సుధ వాటిని కొనలేదు.
సుధ పెన్ను కొనలేకపోవుటకు అనుకూల పర్యవసానాల సంఖ్య = 20
సుధ పెన్ను కొనలేకపోవుటకు సంభావ్యత P(\(\overline{\mathrm{E}}\)) = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{20}{144}=\frac{5}{36}\)
(లేదా)
P (కొనలేనవి) = 1 – P (కొనగలవి)
P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{31}{36}\) = \(\frac{5}{36}\)

ప్రశ్న 13.
ఒకేసారి రెండు పాచికలను దొర్లించి వాటిపై సంఖ్యలను కూడినచో వచ్చు.
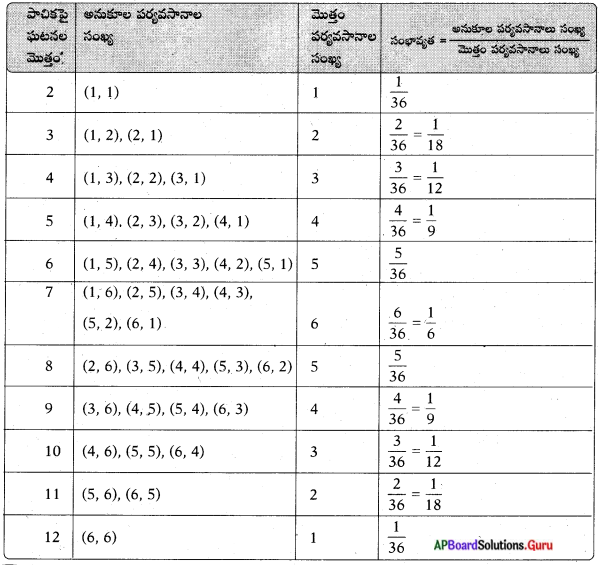
(i) మొత్తాల సంభావ్యతను తెలుపు పట్టికను పూరించండి.

(ii) ఒక విద్యార్థి ఈ ప్రయోగంలో 2,3,4,5,6,7,8,9,10,11,12 అనే 11 పర్యవసానములు ఉన్నవి, కావున ఒక్కొక్క పర్యవసానము యొక్క సంభావ్యత – అన్నాడు. ఈ సమాధానంతో నీవు ఏకీభవిస్తావా? వివరించు.
సాధన.
(i) రెండు పాచికలను దొర్లించిన లభించగల మొత్తం పర్యవసానాల సంఖ్య = 36

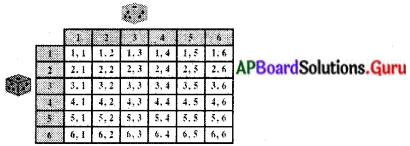
(ii) ఇచ్చిన పట్టిక నుండి (పై పట్టిక నుండి) విద్యార్థి యొక్క వివరణ తప్పు. ఇచ్చట ప్రతిదాని సంభావ్యత \(\frac{1}{11}\) గా లేదు.
రెండు పాచికను దొర్లించినపుడు వచ్చు పర్యవసానాలు 2, 3, 4, …….. 12 లు కాదు.
ఇవి ప్రాథమిక పర్యవసానాలైన (1, 1), (1, 2) ……….. (6, 6) లో కొన్ని ప్రత్యేక ఘటనల పర్యవసానాలు 2, 3, 4, …….. 12.

ప్రశ్న 14.
ఒక రూపాయి నాణెమును 3 సార్లు ఎగురవేసి బొమ్మ, బొరుసులను పరిశీలించాలనుకొన్నారు. అవి మూడు బొమ్మలు లేక బొరుసులు అయితే హనీష్ గెలుస్తాడు. హనీష్ ఓడిపోవడానికి సంభావ్యత కనుగొనండి.
సాధన.
ఒక నాణేన్ని n సార్లు ఎగురవేసిన వచ్చు అనుకూల పర్యవసానాల సంఖ్య = 2ⁿ.
ఒక నాణేన్ని 3 సార్లు పైకి ఎగురవేసిన లభించగల మొత్తం పర్యవసానాల సంఖ్య = 2³ = 8.
అవి ఈ క్రింది విధంగా కలవు.

∴ అన్నీ బొమ్మ మరియు అన్నీ బొరుసు కాని విభిన్న . పర్యవసానాల సంఖ్య = 8 – 2 = 6
∴ హనీష్ ఓడిపోవటానికి గల సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{6}{8}=\frac{3}{4}\)

ప్రశ్న 15.
ఒక పాచికను.రెండుసార్లు దొర్లించారు. కనీసం ఒక్కసారి
(i) 5 పాచికపై కనిపించడానికి
(ii) 5 పాచికపై కనిపించకపోవడానికి సంభావ్యతలు ఎంతెంత?
సాధన.
పాచికను 2 సార్లు దొర్లించిన లభించదగు మొత్తం పర్యవసానాల సంఖ్య = 6² = 36.
పాచికను రెండుసార్లు దొర్లించినపుడు ఏర్పడు పర్యవసానాలు.

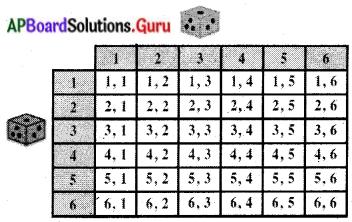
(i) రెండు పాచికలపై ‘5’ కనీసం ఒక సంఖ్యగా వచ్చు అనుకూల పర్యవసానాల సంఖ్య = 11
అవి. (1, 5), (2, 5), (3, 5), (4, 5), (5, 5), (6, 5), (5, 1), (5, 2), (5, 3), (5,4), (5, 6) = 11
∴ P(E) = 5 పాచిక పై కనిపించడానికి సంభావ్యత = అనుకూల పర్యవసానాల సంఖ్య / మొత్తం పర్యవసానాల సంఖ్య
= \(\frac{11}{36}\)

(ii) పాచికపై ‘5’ సంఖ్య కన్పించని (సందర్భాలు) అనుకూల పర్యవసానాలు
(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 6), (4.1), (4, 2), (4, 3), (4, 4), (4, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 6) = 25.

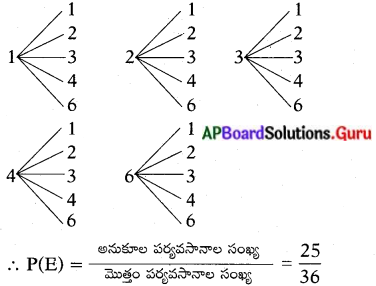
(లేదా)
P(E) పాచికపై 5 కనిపించుటకు సంభావ్యత అయిన P(\(\overline{\mathrm{E}}\)) పాచికపై 5 కనిపించకపోవుటకు సంభావ్యత అవుతుంది.
P(\(\overline{\mathrm{E}}\)) = 1 – P(E)
= 1 – \(\frac{11}{36}\) = \(\frac{25}{36}\)