AP Board 10th Class Maths Solutions Chapter 14 సాంఖ్యకశాస్త్రం InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 14 సాంఖ్యకశాస్త్రం InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 14th Lesson సాంఖ్యకశాస్త్రం InText Questions

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
వర్గీకృత మరియు అవర్గీకృత దత్తాంశానికి సగటును కనుగొనవచ్చు. వీటిలో ఏది అత్యంత ఖచ్చితమైన సగటు అని నీవు భావిస్తావు ? ఎందుకు ? (పేజీ నెం. 327)
సాధన.
వర్గీకృత దత్తాంశం ద్వారా అత్యంత ఖచ్చితమైన సగటును కనుగొనవచ్చును. . ఎందుకనగా వర్గీకృత దత్తాంశం తరగతులుగా విడగొట్టబడి ఉంటుంది. ఆ దత్తాంశం యొక్క పౌనఃపున్యాలు ఆ తరగతి ఆధారంగా నిర్ణయించబడి, ప్రతి ‘ అంశాన్ని పరిగణలోనికి తీసుకొంటాం. కావున, ఇది ఖచ్చితమైన సగటునిస్తుంది.

ప్రశ్న 2.
దత్తాంశ విశ్లేషణకు వర్గీకృత దత్తాంశము ఎప్పుడు అనువైనది ? (పేజీ నెం. 327)
సాధన.
దత్తాంశంలో రాశుల సంఖ్య చాలా ఎక్కువగా ఇచ్చినపుడు వర్గీకృత దత్తాంశం విశ్లేషణకు అనువైనది.

ప్రశ్న 3.
పై మూడు పద్ధతుల ద్వారా సాధించబడిన ఫలితము ఒకటేనా ? (పేజీ నెం. 331)
సాధన.
అవును.

ప్రశ్న 4.
ఒకవేళ x, మరియు f, లు చాలినంత చిన్నగా ఉంటే, : అపుడు ఏ పద్ధతిని ఎన్నుకోవడం అనుకూలమైనది ? (పేజీ నెం. 331)
సాధన.
ప్రత్యక్ష పద్ధతి.

ప్రశ్న 5.
ఒకవేళ x_i మరియు f_i ల విలువలు పెద్ద సంఖ్యలు అయినపుడు ఏ పద్ధతి సరియైన పద్ధతి ? (పేజీ నెం. 331)
సాధన.
సంక్షిప్త విచలన పద్ధతి.

ఇవి చేయండి:

ప్రశ్న 1.
ఈ క్రింది దత్తాంశానికి బాహుళకాన్ని కనుక్కోండి.
a) 5, 6, 9, 10, 6, 12, 3, 6, 11, 10, 4, 6, 7.
b) 20, 3, 7, 13, 3, 4, 6, 7, 19, 15, 7, 18, 3.
c) 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6. (పేజీ.నెం. 334)
సాధన.
బాహుళకం
a) 6 (తరచుగా వచ్చు విలువ)
b) 3, 7 (ద్విబాహుళకం)
c) బాహుళకం లేదు. బాహుళక రహిత దత్తాంశము.

ప్రశ్న 2.
బాహుళకము ఎల్లప్పుడు దత్తాంశమునకు మధ్యలో
ఉంటుందా ? (పేజీ నెం. 334)
సాధన.
ఉండనవసరం లేదు.

ప్రశ్న 3.
10 క్రికెట్ మ్యా చ్ లో ఒక బౌలర్ తీసిన వికెట్లు క్రింది విధంగా ఉన్నాయి. 2, 6, 4, 5, 0, 2, 1, 3, 2, 3 (ఉదాహరణ – 4). ఈ దత్తాంశానికి మరొక రాశిని చేర్చగా బాహుళకము మారుతుందా ? వ్యాఖ్యానించండి. (పేజీ నెం. 334)
సాధన.
దత్తాంశానికి మరో అంశం కొత్తగా కలిపినపుడు దాని బాహుళకం – మారుతుందా లేదా అనేది మనం చేర్చిన దత్తాంశంపై ఆధారపడుతుంది. ఉదాహరణకు మనకు ఇచ్చిన దత్తాంశం నందు 0, 1, 2, 2, 2, 3, 3, 4, 5, 6 అను దానిలో 2 (3 సార్లు) ఉన్నది. కావున దీని బాహుళకం = 2.

అయితే మనం ఈ దత్తాంశానికి “3” అనే అంశాన్ని చేర్చితే ఆ దత్తాంశం 0, 1, 2, 2, 2, 3, 3, 3, 4, 5, 6 గా మారును. అపుడు ఈ క్రొత్త దత్తాంశానికి 2 మరియు 3 లు రెండూ కూడా బాహుళకం అగును. అపుడు దీనిని ద్విబాహుళక దత్తాంశం అందురు, కావున ‘3’ చేర్చుటువల్ల బాహుళకం మారును. 3 కాకుండా ఏ ఇతర అంశాన్ని చేర్చినా బాహుళకం మారదు అని గుర్తించాలి.

ప్రశ్న 4.
ఒకవేళ ఉదాహరణ-4లోని రాశులలోని గరిష్ఠవిలువ ‘8’కి మారిన, దాని ప్రభావం అట్టి దత్తాంశం యొక్క బాహుళకంపై ఉంటుందా ? .వ్యాఖ్యానించుము. (పేజీ నెం. 334)
సాధన.
4లోని రాశులలో, గరిష్ట విలువ 8కి మారిన, దాని ప్రభావం బాహుళకంపై ఉండదు, బాహుళకం మారదు. గరిష్ఠ, కనిష్ఠ విలువలకు. బాహుళకం మారనవసరం లేదు.”

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
సందర్భాన్ని బట్టి మనము తరగతిలోని విద్యార్థుల అందరి సరాసరి మార్కులు, లేక ఎక్కువమంది విద్యార్థులు పొందిన మార్కులు కనుగొంటాము. . . (పేజీ నెం. 336)
a) మొదటి సందర్భంలో మనం ఏ కేంద్రీయస్థానపు విలువను కనుక్కొంటాం ?
సాధన.
సగటు.
b) రెండవ సందర్భంలో మనం ఏ కేంద్రీయస్థానపు విలువను కనుక్కొంటాం ?
సాధన. బాహుళకము.

ప్రశ్న 2. వేరువేరు తరగతి అంతరాలు గల దత్తాంశమునకు కూడా బాహుళకము’ను కనుగొనవచ్చునా ? (పేజీ నెం. 336)
సాధన.
లేదు. విభిన్న తరగతి అంతరాలతో బాహుళకం కనుగొనలేము.

ఉదాహరణలు:

ప్రశ్న 1.
ఒక పాఠశాలలోని 10వ తరగతికి చెందిన 30 మంది విద్యార్థులు గణితంలో పొందిన మార్కులు పట్టికలో ఇవ్వబడ్డాయి. విద్యార్థులు పొందిన మార్కుల సగటు కనుక్కోండి. (పేజీ నెం. 324)

సాధన.
పై దత్తాంశాన్ని క్రింద చూపిన పట్టికలో తిరిగి వ్రాయగా,

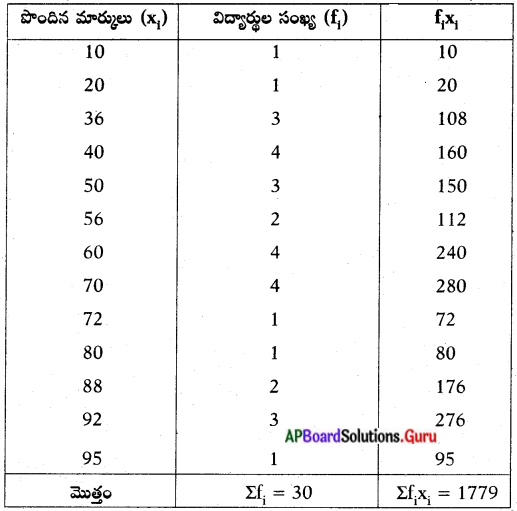
కాబట్టి, \(\overline{\mathbf{x}}\) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
= \(\frac{1779}{30}\) = 59.3
∴ మార్కుల సగటు = 59.3.

ప్రశ్న 2.
భారతదేశములోని వివిధ రాష్ట్రాలు మరియు కేంద్రపాలిత ప్రాంతాలకు చెందిన గ్రామీణ ప్రాంత ప్రాథమిక పాఠశాలల్లో గల మహిళా ఉపాధ్యాయుల శాతముల వివరములు ఈ క్రింది పట్టికలో పొందుపరచబడినాయి. పై మూడు పద్దతులనుపయోగించి మహిళా ఉపాధ్యాయుల సగటు శాతాన్ని కనుక్కోండి. (పేజీ నెం. 330)

(NCERT వారు నిర్వహించిన 7వ అఖిలభారతీయ పాఠశాల విద్యా సర్వే గణాంకాల ప్రకారం)
సాధన.
తరగతి మధ్య విలువ x_i కనుగొని, దానిని పట్టికలో పొందుపరుచుదాం.
ఇచ్చట a = 50, h = 10,
అపుడు d_i = x_i – 50 మరియు u_i = 10 –
ఇపుడు మనము d_i మరియు u_i విలువలను కనుగొని పట్టికలో పొందుపరచగా

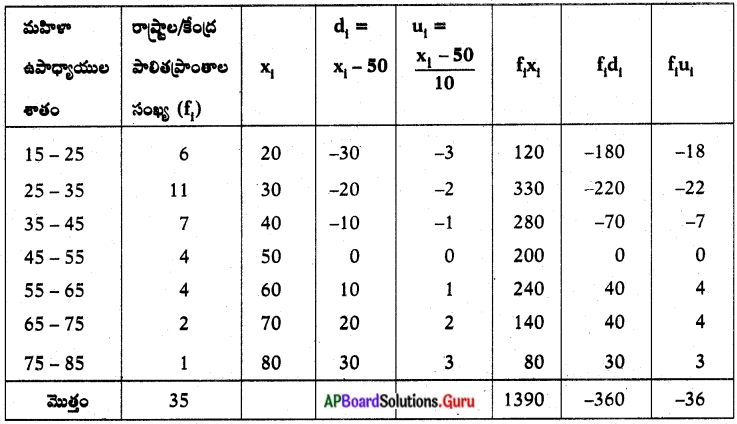
పై పట్టిక నుండి, Σf_i = 35, Σf_ix_i = 1390, Σf_id_i = – 360, Σf_iu_i = – 36.
ప్రత్యక్ష పద్ధతి ద్వారా (\(\overline{\mathbf{x}}\)) = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
= 1390 = 39.71
ఊహించిన సగటు పద్ధతి ద్వారా (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{d}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
= 50 + \(\frac{-360}{35}\)
= 50 – 10.29 = 39.71
సోపాన విచలన పద్ధతి ద్వారా (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 50 + \(\frac{-36}{35}\) × 10
= 39.71
∴ గ్రామీణ ప్రాంత ప్రాథమిక పాఠశాలల్లో గల మహిళా ఉపాధ్యాయుల సగటు శాతము = 39.71.

ప్రశ్న 3.
వన్డే క్రికెట్ ఆటలో బౌలర్లు సాధించిన వికెట్ల వివరాలను ఈ క్రింది పౌనఃపున్య విభాజన పట్టికలో చూపించనైనది. సరియైన పద్ధతిని ఎంచుకొని బౌలర్లు సాధించిన సగటు వికెట్లను కనుగొనుము. ఇట్టి సగటు యొక్క ప్రాముఖ్యత ఏమిటి? (పేజీ నెం. 331)

సాధన.
ఇచ్చట తరగతి పొడవులు వేరువేరుగా ఉన్నాయి, మరియు x_i విలువలు పెద్దవిగా ఉన్నాయి. అయినప్పటికినీ సగటు కనుగొనడానికి సంక్షిప్త విచలన పద్ధతినే ఎంచుకుందాము; ఇచ్చట a = 200 మరియు మీ = 20.

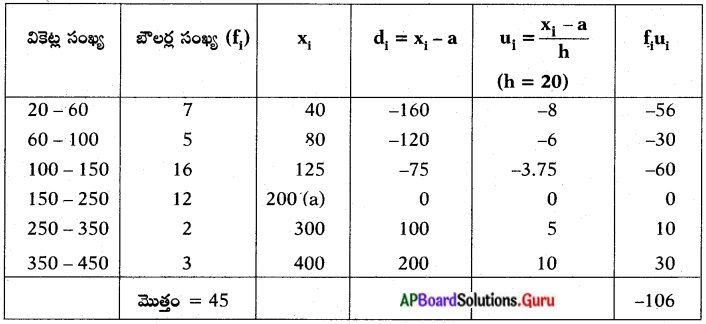
అందువల్ల (\(\overline{\mathbf{x}}\)) = a + \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{u}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\) × h
= 200 + \(\frac{-106}{45}\) × 20
= 200 – 47.11 = 152.89
∴ 45 మంది బౌలర్లు వన్డే క్రికెట్ లో సాధించిన వికెట్ల సగటు = 152.89.

ప్రశ్న 4.
10 క్రికెట్ మ్యా చ్ లలో ఒక బౌలర్ తీసిన వికెట్లు క్రింది కుటుంబ విధంగా ఉన్నాయి. 2, 6, 4, 5, 0, 2, 1, 3, 2, 3. కుటుంబా ఈ దత్తాంశానికి ‘బాహుళకాన్ని’ కనుక్కోండి. – (పేజీ నెం. 334)
సాదన.
దత్తాంశములోని అంకెలను (రాశులను) ఒక పౌన క్రమపద్ధతిలో అమర్చగా అనగా 0, 1, 2, 2, 2, 3, బాప 3, 4, 5, 6.
ఇపుర పై దత్తాంశంను పరిశీలించగా, ఎక్కువ మ్యాచుల్లో బాప బౌలర్ ‘2’ వికెట్లను తీసినట్లుగా స్పష్టంగా తెలియుచున్నది. (అనగా 3 సార్లు).
అందువల్ల ఇవ్వబడిన దత్తాంశం యొక్క బాహుళకము 2.

ప్రశ్న 5.
ఒక ఆవాస ప్రాంతంలో కొంతమంది విద్యార్థుల బృందం బాప 20 కుటుంబాలను సర్వే చేసి, కుటుంబ సభ్యుల పౌన: సంఖ్యను ఈ క్రింద చూపిన పౌనఃపున్య విభాజన పట్టికలో చూపనైనది. (పేజీ నెం. 335)

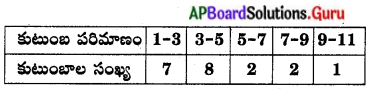
ఈ దత్తాంశానికి ‘బాహుళకాన్ని’ కనుక్కోండి.
సాధన.
ఇచ్చట, గరిష్ఠ తరగతి పౌనఃపున్యము 8, ఈ పౌనఃపున్యానికి సంబంధించిన తరగతి 3-5. అందువల్ల బాహుళక తరగతి 3-5.
ఇపుడు,
బాహుళక తరగతి = 3-5,
మధ్యంతర తరగతి యొక్క దిగువహద్దు (l) = 3,
తరగతి పొడవు (h) = 2
బాహుళక తరగతి పౌనఃపున్యము (f₁) = 8,
బాహుళక తరగతికి ముందున్న తరగతి యొక్క
పౌనఃపున్యము (f₀) = 7,
బాహుళక తరగతికి తరువాత నున్న తరగతి యొక్క .
పౌనఃపున్యము (f₂) = 2.
పై విలువలను, ఈ క్రింది సూత్రములో ప్రతిక్షేపించుదాం.
బాహుళకం = l + \(\left(\frac{f_{1}-f_{0}}{2 f_{1}-f_{0}-f_{2}}\right)\) × h
= 3 + \(\left(\frac{8-7}{2 \times 8-7-2}\right)\) × 2
ఆ పై దత్తాంశం యొక్క బాహుళకము 3.286. (2×8-7-2).

ప్రశ్న 6.
ఒక తరగతిలో 30 మంది విద్యార్థులు ఒక గణిత పరీక్షలో పొందిన మార్కులు పౌనఃపున్య విభాజన పట్టిక ఈ క్రింది నీయబడినది. ఈ దత్తాంశానికి ‘బాహుళకము’ను కనుగొనుము. అదే విధంగా బాహుళకము మరియు సగటులను పోల్చి, వ్యాఖ్యానించుము. (పేజీ నెం. 335) తరగతి అంతరం విద్యార్థుల సంఖ్య తరగతి మధ్య విలువ

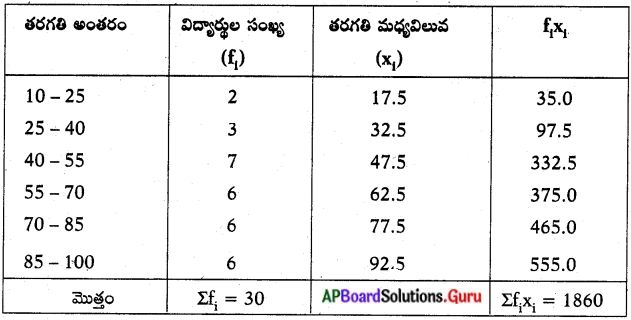
సాధన.
దత్తాంశములోని ఎక్కువ మంది విద్యార్థులు (7గురు) ’40-55′ తరగతి అంతరంలో మార్కులు సాధించియున్నారు.
కనుక ’40-55′ అనేది బాహుళక తరగతి అవుతుంది.
మధ్యంతర తరగతి యొక్క దిగువ హద్దు (l) = 40,
తరగతి పొడవు (h) = 15,
బాహుళక తరగతి యొక్క పౌనఃపున్యము (f₁) = 7,
బాహుళక తరగతికి ముందున్న తరగతి పౌనఃపున్యము (f₀) = 3,
బాహుళక తరగతికి తరువాత నున్న తరగతి పౌనఃపున్యము (f₂) = 6.
బాహుళకము = l + \(\left(\frac{\mathrm{f}_{1}-\mathrm{f}_{0}}{2 \mathrm{f}_{1}-\mathrm{f}_{0}-\mathrm{f}_{2}}\right)\) × h
= 40 + \(\left(\frac{7-3}{2 \times 7-6-3}\right)\) × 15
= 40 + 12 = 52.

వ్యాఖ్యానం (Interpretation) :
పై దత్తాంశానికి బాహుళకము 52; అదే విధంగా సగటు 62 (ఉదాహరణ – 1, ద్వారా) అని తెలియుచున్నది. అనగా తరగతిలోని 52 మార్కులు పొందిన విద్యార్థులు ఎక్కువ మంది ఉన్నారని, ఒక్కొక్క విద్యార్థి యొక్క సగటు మార్కులు 62 అని తెలుస్తుంది.

ప్రశ్న 7.
ఒక పాఠశాలలోని 10వ తరగతి బాలికల ఎత్తు గురించి చేసిన సర్వే ఫలితాలు కింది పట్టికలో ఇవ్వబడ్డాయి. వారి ఎత్తుల మధ్యగతము కనుగొనండి (పేజీ నెం. 342)

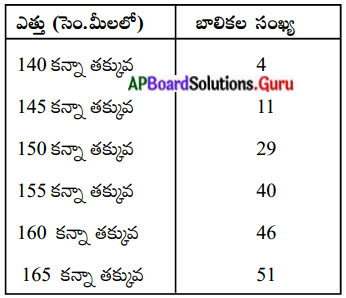
సాధన.
మధ్యగతము కనుగొనుటకు మొదట తరగతి అంతరాలను, వాటి సంబంధిత పౌనఃపున్యములను కనుగొనవలెను. ఇచ్చిన విలువలు ఎగువహద్దు కన్నా తక్కువ సంచిత పౌనఃపున్యములు కావు, ఎత్తులు 140, 145, 150, …, లు ఎగువ హద్దులు, అనగా తరగతి అంతరాలు 140 కన్నా తక్కువ, 140 – 145, 145 – 150 ……. అవుతాయి.

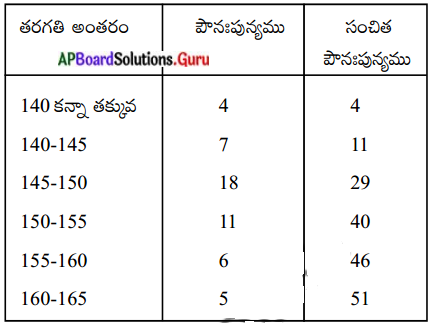
పట్టికను పరిశీలిస్తే 140 కన్నా తక్కువ పొడవు గల బాలికల సంఖ్య 4 అనగా 140 కన్నా తక్కువ తరగతి యొక్క పౌనఃపున్యము 4.
145 సెం.మీ కన్నా తక్కువ పొడవు గలవారు 11 మంది. అనగా 140 – 145 తరగతి పౌనఃపున్యం 11 – 4 = 7.
ఇదే విధంగా మిగిలిన పౌనఃపున్యములను లెక్కించవచ్చు.
దత్తాంశంలోని రాశుల సంఖ్య n = 51,
\(\frac{1}{4}-\frac{1}{9}\)
\(\frac{n}{2}=\frac{51}{2}\) = 25.5
22 దత్తాంశంలోని 25. 5వ రాశి 145-150 తరగతికి చెందుతుంది.
∴ 145 – 150 మధ్యంతర తరగతి. మధ్యగత తరగతి దిగువహద్దు l = 145,
మధ్యగత తరగతికి ముందు తరగతి cf = 11,
సంచిత పౌనఃపున్యం మధ్యగత తరగతి యొక్క పౌనఃపున్యము f = 18,
మధ్యగత తరగతి పొడవు h = 5.
సూత్రమును ఉపయోగించి మధ్యగతం = l + \(\frac{\left(\frac{\mathrm{n}}{2}-\mathrm{cf}\right)}{\mathrm{f}}\) × h
= 145 + \(\frac{(25.5-11)}{18}\) × 5
= 145 + \(\frac{72.5}{4}\)
= 149.03
∴ బాలికల పొడవుల యొక్క మధ్యగతము 149.03 సెం.మీ అనగా తరగతిలో 50% మంది బాలికలు 149.03 సెం.మీ కన్నా ఎక్కువ పొడవు కలిగి ఉంటారు.
మిగిలిన 50% మంది 149.03 సెం.మీ. కన్నా తక్కువ ఫొడవు కలిగి ఉంటారు.

ప్రశ్న 8.
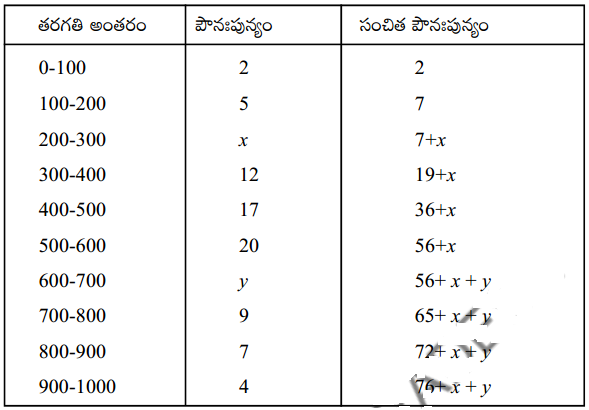
క్రింది దత్తాంశము యొక్క మధ్యగతము 525 మరియు దత్తాంశంలోని రాశుల మొత్తం 100 అయిన x, y విలువలను కనుగొనండి. (పట్టికలో CI అనగా తరగతి అంతరం, Fr అనగా పౌనఃపున్యం) (పేజీ నెం. 344)

సాధన.
దత్తాంశంలోని రాశుల సంఖ్య n = 100 అని ఇవ్వబడింది.
76 + x + y = 100, i.e., x + y = 24 (1)
మధ్యగతం 525 అను రాశి 500 – 600 తరగతికి చెందుతుంది.
కావున, l = 500, f = 20, cf = 36 + x, h = 100 .
సూత్రము ఉపయోగించి మధ్యగతము = l + \(\frac{\left(\frac{\mathrm{n}}{2}-\mathrm{cf}\right)}{\mathrm{f}}\) × h
525 = 500 + \(\frac{50-36-x}{20}\) × 100
525 – 500 = (14 – x) × 5
25 = 70 – 5x.
5x = 70 – 25 = 45
∴ x = 9.
సమీకరణం (1) నుండి 9 + y = 24
∴ y = 15.

గమనిక : వేరువేరు తరగతి అంతరాలు గల దత్తాంశమునకు కూడా ఇదే సూత్రమును ఉపయోగించి మధ్యగతమును కనుగొనవచ్చు.

ప్రశ్న 9.
ఒక ప్రాంతములోని 30 అంగళ్ళ యొక్క సంవత్సర ఆదాయములు క్రింది పట్టిక రూపంలో ఇవ్వబడ్డాయి. (పేజీ నెం. 349)

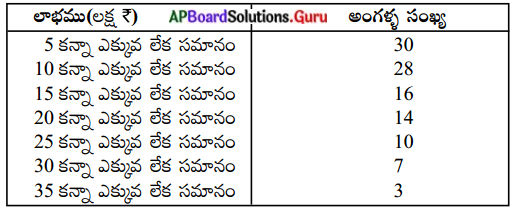
పై దత్తాంశమునకు రెండు ఓజీవ్ వక్రాలు గీయండి. అందు నుండి , లాభముల యొక్క మధ్యగతము కనుగొనండి.
సాధన.
ఇచ్చిన దత్తాంశములోని విలువలు దిగువ హద్దులు, సంబంధిత అవరోహణ సంచిత పౌనఃపున్యములు. వీటితో మొదట అవరోహణ సంచిత పౌనఃపున్య వక్రము గీయుటకు అనువైన స్కేలు తీసుకొని
X-అక్షముపై దిగువహద్దులను, Y- అక్షముపై సంచిత లాభము పౌనఃపున్యములను గుర్తించి వాటిని కలుపుతూ సరళ వక్రమును గీయాలి.. ఇది అవరోహణ సంచిత
పౌనఃపున్య వక్రము అవుతుంది. ఇప్పుడు ఇచ్చిన దత్తాంశము నుండి తరగతి అంతరాలు, పౌనఃపున్యములు, ఆరోహణ సంచిత పౌనఃపున్యములను తయారు చేయగా ఆరోహణ సంచిత పౌనఃపున్యం

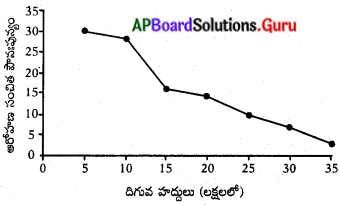
పై దత్తాంశమునుండి ఏర్పడు బిందువులు (10, 2), (15, 14), (20, 16), (25, 20), (30, 23), (35, 27), (40, 30) బిందువులను అదే గ్రాఫ్ పై గుర్తించి సరళ వక్రముతో కలుపగా ఆరోహణ సంచిత పౌనఃపున్య వక్రము ఏర్పడుతుంది.

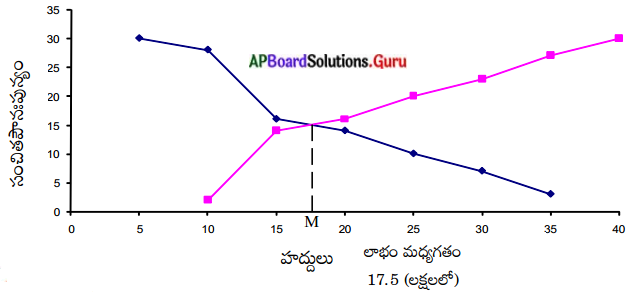
ఈ రెండు వక్రములు పరస్పరం ఖండించుకొన్న బిందువు నుండి X-అక్షం మీదకు లంబమును గీయగా, ‘ఆ లంబపాదము 17.5 అని గుర్తించవచ్చు. అనగా దత్తాంశము యొక్క మధ్యగతము (M) = 17.5 లక్షల రూపాయలు.