AP Board 10th Class Maths Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.1

ప్రశ్న 1.
గ్రాఫీలు గీయకుండా, \(\frac{a_{1}}{a_{2}}\), \(\frac{b_{1}}{b_{2}}\), \(\frac{c_{1}}{c_{2}}\) నిష్పత్తులను పోల్చి, కింద ఇచ్చిన రేఖా సమీకరణాల జతలు ఖండన రేఖలో, సమాంతర రేఖలో లేదా ఏకీభవించే రేఖలో కనుగొనుము.
a) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
సాధన.
5x – 4y + 8 = 0
7x + 6y – 9 = 0
a₁ = 5, b₁ = – 4, c₁ = 8
a₂ = 7, b₂ = 6, c₂ = – 9
\(\frac{a_{1}}{a_{2}}=\frac{5}{7}\); \(\frac{b_{1}}{b_{2}}=\frac{-4}{6}\); \(\frac{c_{1}}{c_{2}}=\frac{8}{-9}\)

\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) కావున ఖండన రేఖలు.

b) 9x + 3y + 12 = 0; 18x + 6y + 24 = 0 a b1 1 విపతులను
సాధన.
9x + 3y + 12 = 0 , 18x + 6y + 24 = 0
a₁ = 9, b₁ = 3, c₁ = 12
a₂ = 18, b₂ = 6, c₂ = 24

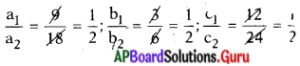
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\) కావున ఏకీభవించే రేఖలు

c) 6x – 3y + 10 = 0; 2x – y + 9 = 0
సాధన.
6x – 3y + 10 = 0; 2x-y + 9 = 0
a₁ = 6, b₁ = – 3, c₁ = 10
a₂ = 2, b₂ = – 1, c₂ = 9
\(\frac{a_{1}}{a_{2}}=\frac{6}{2}\) = 3;

\(\frac{b_{1}}{b_{2}}=\frac{-3}{-1}\) = 3;

\(\frac{c_{1}}{c_{2}}=\frac{10}{9}\)
\(\frac{a_{1}}{a_{2}}\) = \(\frac{b_{1}}{b_{2}}\) ≠ \(\frac{c_{1}}{c_{2}}\) కావున సమాంతర రేఖలు.

ప్రశ్న 2.
కింద ఇచ్చిన సమీకరణాల జతలు సంగత సమీకరణాలో అసంగత సమీకరణాలో సరిచూడుము. వాటిని రేఖాచిత్ర పద్ధతిలో (గ్రాఫ్ పద్ధతిలో) సాధించుము
a) 3x + 2y = 8
2x – 3y = 1
సాధన.
ఇచ్చిన సమీకరణాలు 3x + 2y = 8 మరియు 2x – 3y = 1
\(\frac{a_{1}}{a_{2}}=\frac{3}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{2}{-3}\);

\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\)

కావున ఇచ్చిన సమీకరణాలు సంగత సమీకరణాలు

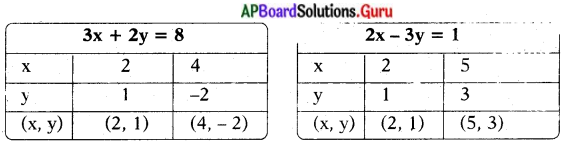
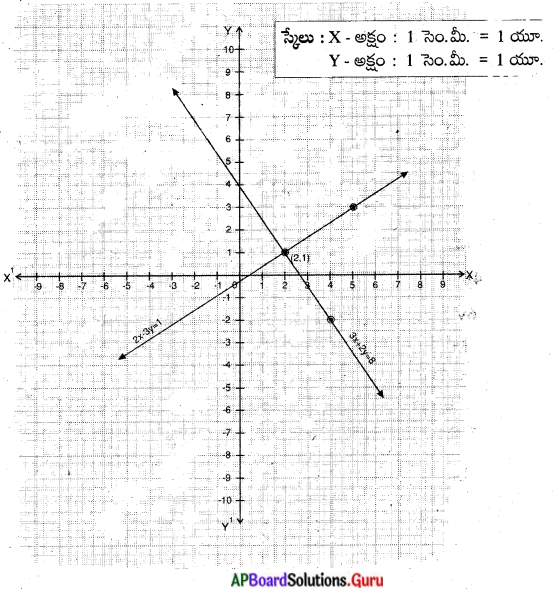
ఇచ్చిన సమీకరణాల జత ఖండనరేఖలు. కావున ఏకైక సాధన ఉంటుంది.
∴ (x, y) = (2, 1)

b) 2x – 3y = 8
4x – 6y = 9
సాధన.
2x – 3y = 8 ⇒ 2x – 3y – 8 = 0
4x – 6y = 9 ⇒ 4 – 6y – 9 = 0 .
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{-3}{-6}=\frac{1}{2}\);;

\(\frac{c_{1}}{c_{2}}=\frac{-8}{-9}=\frac{8}{9}\)

\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\), కావున ఇచ్చిన సమీకరణాలు అసంగత సమీకరణాలు a, 2x – 3y = 8
-3y = 8 – 2x
3y = 2x – 8
y = \(\frac{2 x-8}{3}\)
4x – 6y = 9
-6y = 9 – 4x
6y = 4x – 9
y = \(\frac{4 x-9}{6}\).

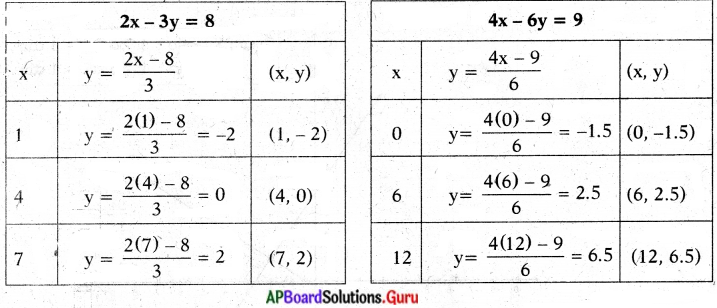
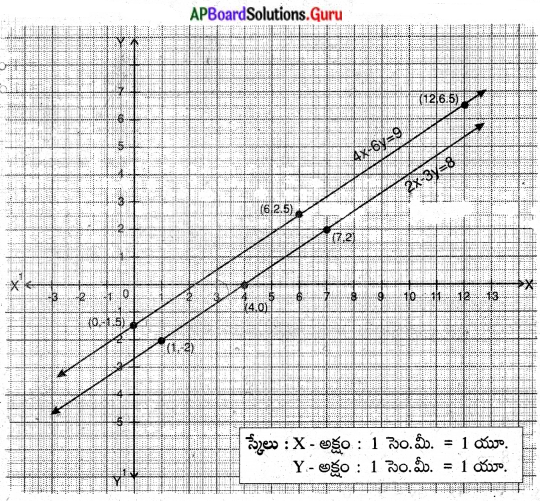
ఇచ్చిన సమీకరణాల జత సమాంతరరేఖలు. కావున సాధన ఉండదు.

c) \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
9x – 10y = 12
సాధన.
ఇచ్చిన సమీకరణాలు \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 మరియు 9x – 10y = 12
ఇప్పుడు, \(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7
⇒ \(\frac{9 x+10 y}{6}\) = 7
⇒ 9x + 10y = 42
9x – 10y = 12
\(\frac{a_{1}}{a_{2}}=\frac{9}{9}=\frac{1}{1}\);

\(\frac{b_{1}}{b_{2}}=\frac{10}{-10}=\frac{1}{-1}\); మరియు

\(\frac{c_{1}}{c_{2}}=\frac{-42}{-12}=\frac{7}{2}\)

∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\), కావున సమీకరణాలు సంగత సమీకరణాలు.

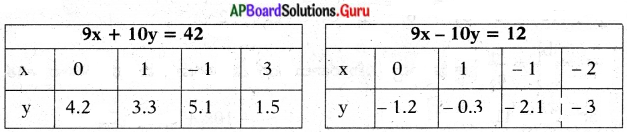
ఇచ్చిన సమీకరణాల జత ఖండనరేఖలు. కావున ఏకైక సాధన ఉంటుంది.
∴ (x, y) = (3.1, 1.4)

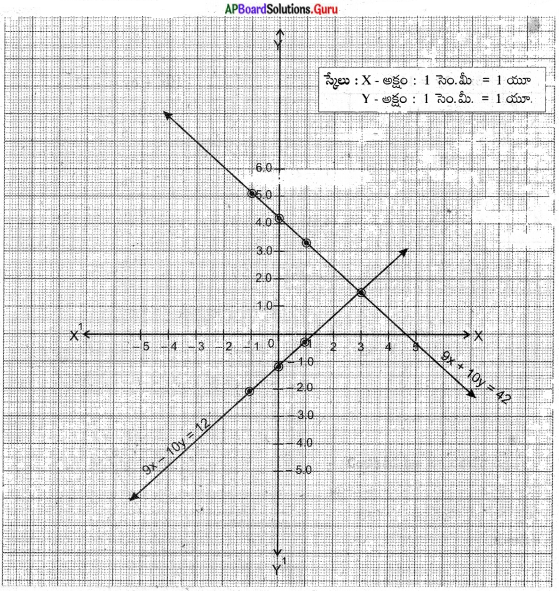
d) 5x + 3y = 11
– 10x + 6y = – 22
సాధన.
5x – 3y = 11 ⇒ 5x – 3y – 11 = 0
-10x + 6y = – 22⇒ – 10x + 6y + 22 = 0
a₁ = 5, b₁ = – 3, c₁ = – 11
a₂ = – 10, b₂ = 6, c₂ = 22
\(\frac{a_{1}}{a_{2}}=\frac{5}{-10}=\frac{-1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{-3}{6}=\frac{-1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{11}{-22}=\frac{-1}{2}\)

∴ \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\), కావున ఇచ్చిన సమీకరణాలు సంగత సమీకరణాలు మరియు పరస్పరాధారిత సమీకరణాలు.
5x – 3y = 11
– 3y – 11 = 5x
y = \(\frac{5 x-11}{3}\)

– 10x + 6y = – 22
6y = 10x – 22
y = \(\frac{10 x-22}{6}\)

∴ ఇచ్చిన సమీకరణాల జత ఏకీభవించే రేఖలు కావున అనంత సాధనలు ఉంటాయి. రేఖపై గల అన్ని బిందువులు సాధనలు అవుతాయి.

e) \(\frac{4}{3}\)x + 2y = 8 ; 2x + 3y = 12
సాధన.
\(\frac{4}{3}\)x + 2y = 8 ⇒ \(\frac{4}{3}\)x + 2y – 8 = 0
2x + 3y = 12 ⇒ 2x + 3y – 12 = 0
a₁ = \(\frac{4}{3}\), b₁ = 2, c₁ = – 8
a₂ = 2, b₂ = 3, c₂ = – 12

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\), కావున ఇచ్చిన సమీకరణాలు
సంగత సమీకరణాలు మరియు పరస్పరాధారిత సమీకరణాలు.
\(\frac{4}{3}\)x + 2y = 8
ఇరువైపులా 3తో గుణించగా
6y = 24 – 4x
y = \(\frac{24-4 x}{6}\)

2x + 3y = 12
3y = 12 – 2x
y = \(\frac{12-2 x}{3}\)

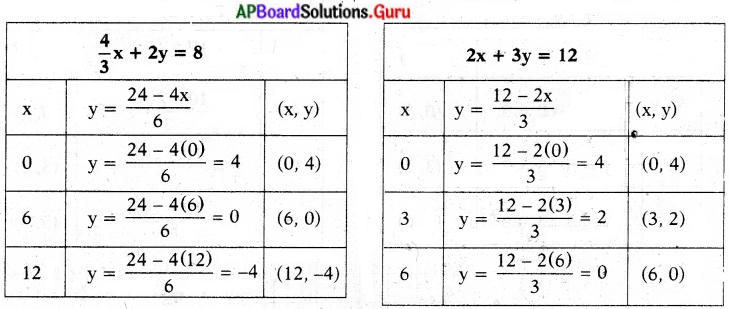
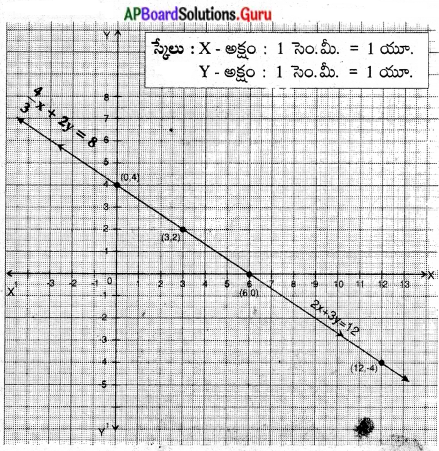
∴ ఇచ్చిన సమీకరణాల జత ఏకీభవించే రేఖలు. కావున అనంత సాధనలు ఉంటాయి. రేఖ పై గల అన్ని బిందువులు సాధనలు అవుతాయి.

f) x + y = 5
2x + 2y = 10
సాధన.
x + y = 5 ⇒ x + y – 5 = 0.
2x + 2y – 10 ⇒ 2x + 2y – 10 = 0
a₁ = 1, b₁ = 1, c₁ = -5
a₂= 2, b₂ = 2, c₂ = – 10
\(\frac{a_{1}}{a_{2}}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-5}{-10}=\frac{1}{2}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\), కావున ఇచ్చిన సమీకరణాలు సంగత సమీకరణాలు మరియు పరస్పరాధారిత సమీకరణాలు.
x + y = 5
y = 5 – x

2x + 2y = 10
2y = 10 – 2x
y = \(\frac{10-2 x}{2}\)

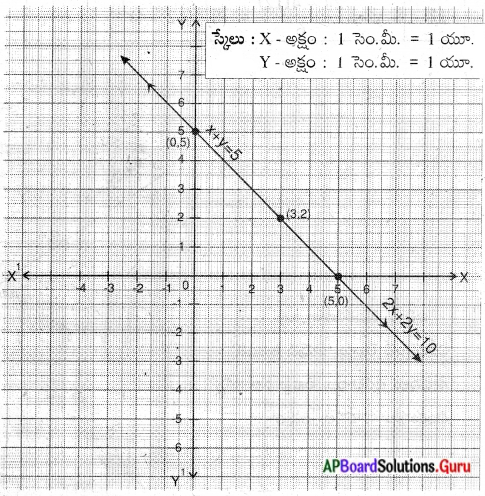
∴ ఇచ్చిన సమీకణాల జత ‘ఏకీభవించే రేఖలు. కావున అనంత సాధనలు ఉంటాయి. రేఖపై గల అన్ని బిందువులు సాధనలు అవుతాయి.

g) x – y = 8.
3x – 3y = 16
సాధన.
x – y = 8 ⇒ x – y – 8 = 0
3x – 3y = 16 ⇒ 3x – 3y = 16
a₁ = 1, b₁ = – 1, c₁ = – 8
a₂ = 3, b₂ = – 3, c₂ = – 16
\(\frac{a_{1}}{a_{2}}=\frac{1}{3}\);

\(\frac{b_{1}}{b_{2}}=\frac{-1}{-3}=\frac{1}{3}\); మరియు

\(\frac{c_{1}}{c_{2}}=\frac{8}{16}=\frac{1}{2}\)

∴ \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)
కావున ఇచ్చిన సమీకరణాలు అసంగత సమీకరణాలు.
x – y = 8
y = x – 8

3x – 3y = 16
– 3y = 16 – 3x
y = \(\frac{3 x-16}{3}\)

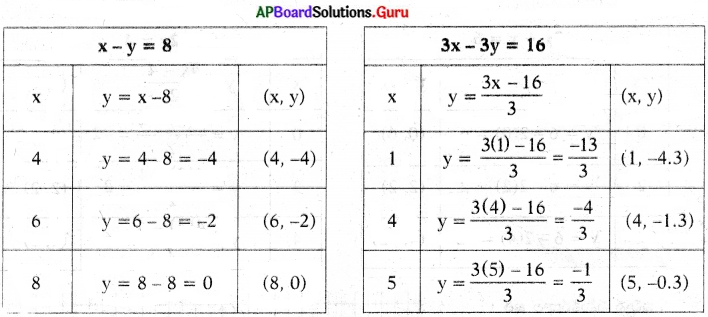
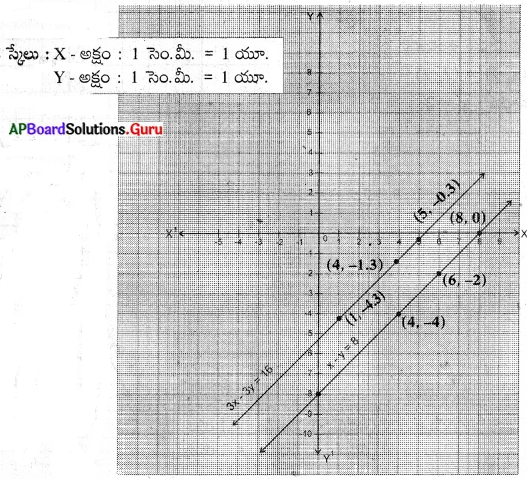
∴ ఇచ్చిన సమీకరణాల జత సమాంతర రేఖలు. కావున సాధన ఉండదు.

h) 2x + y – 6 = 0
4x-2y – 4 = 0
సాధన.
2x + y – 6 = 0;
4x – 2y – 4 = 0
a= 2, b = 1, c = – 6 ;
a = 4, b = – 2, c = – 4
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{1}{-2}=\frac{-1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-6}{-4}=\frac{3}{2}\)

∴ \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\), కావున ఇచ్చిన సమీకరణాలు సంగత సమీకరణాలు
2x + y – 6 = 0
y = 6 – 2x

4x – 2y – 4 = 0
– 2y = 4 – 4x
y = \(\frac{4 x-4}{2}\)

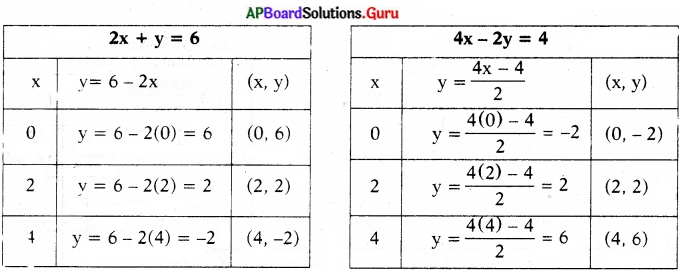
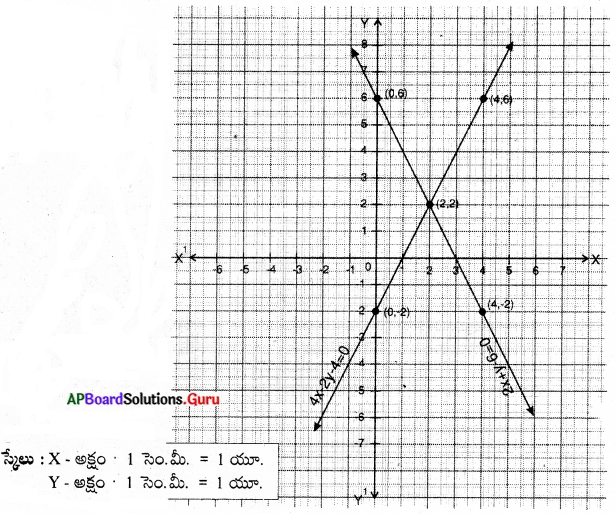
∴ ఇచ్చిన సమీకరణాల జత ఖండనరేఖలు, కావున ఏకైక సాధన ఉంటుంది.
(x, y) = (2, 2)
సాధన : x = 2, y = 2

i) 2x – 2y – 2 = 0
4x – 4y -5 = 0
సాధన.
2x – 2y – 2 = 0
4x – 4y – 5 = 0
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{a_{1}}{a_{2}}=\frac{-2}{-4}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-2}{-5}=\frac{2}{5}\)

∴ \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)
కావున ఇచ్చిన సమీకరణాలు అసంగత సమీకరణాలు.
2x – 2y – 2 = 0
– 2y = 2 – 2x
2y = 2x – 2
y = \(\frac{2 x-2}{2}\)

4x – 4y – 5 = 0 L
– 4y = 5 – 4x
y = \(\frac{4 x-5}{4}\)

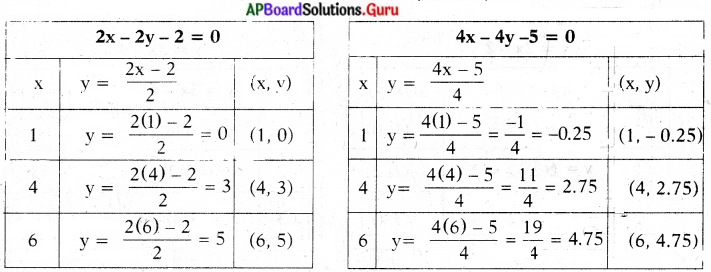
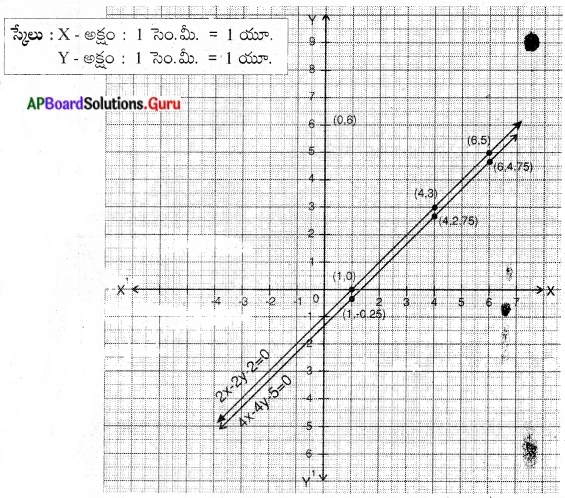
∴ ఇచ్చిన సమీకరణాల జత సమాంతర రేఖలు. కావున సాధన ఉండదు.

ప్రశ్న 3.
నేహ కొన్ని ప్యాంటులను మరియు స్కర్టులను కొనడానికి దుకాణమునకు వెళ్ళినది. ఆమె మిత్రురాలు ప్యాంటులు ఎన్ని, స్కర్టులు ఎన్ని కొన్నావని అడుగగా ఆమె ఇలా జవాబిచ్చింది. “నేను కొన్న స్కర్టుల సంఖ్య, ప్యాంట్ల సంఖ్య రెట్టింపు కన్నా రెండు తక్కువ. అలాగే స్కర్టుల సంఖ్య ప్యాంట్ల సంఖ్యకు మూడు రెట్లు కన్నా నాలుగు తక్కువ”. నేహ ఎన్ని ప్యాంటులు, ఎన్ని స్కర్టులు కొన్నదో తెలుసుకోవడంలో ఆమె మిత్రురాలికి సహాయం చేయండి. –
సాధన.
నేహ కొన్న ప్యాంట్ల సంఖ్య = x అనుకొనుము.
స్కర్టుల సంఖ్య = y అనుకొనుము.
నేహ కొన్న స్కర్టుల సంఖ్య ప్యాంట్ల సంఖ్య రెట్టింపు కన్నా రెండు తక్కువ.
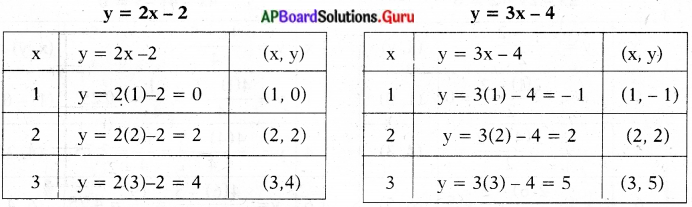
y = 2x – 2 …………(1)
మరియు నేహ కొన్న స్కర్టుల సంఖ్య ప్యాంట్ల సంఖ్యకు మూడురెట్ల కన్నా నాలుగు తక్కువ.
y = 3x – 4 ………….(2)
y = 3x – 4

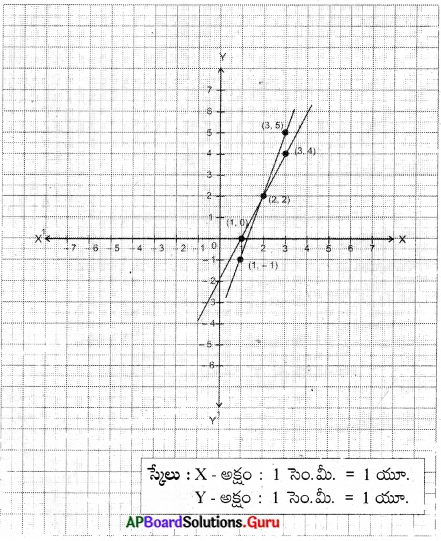
(x, y) = (2, 2)
∴ నేహ కొన్న ప్యాంట్ల సంఖ్య = 2
స్కర్టుల సంఖ్య = 2.

ప్రశ్న 4.
రెండు చరరాశులలో రేఖీయ సమీకరణాల జత) 4. పదవతరగతి చదివే 10 మంది విద్యార్థులు ఒక గణిత క్విజ్ లో పాల్గొన్నారు. దానిలో పాల్గొన్న బాలికల సంఖ్య, బాలుర సంఖ్య కన్నా 4 ఎక్కువ అయిన ఆ క్విజ్ లో పాల్గొన్న బాలికల సంఖ్యను, బాలుర సంఖ్యను కనుగొనండి.
సాధన.
బాలికల సంఖ్య = x
బాలుర సంఖ్య = y అనుకుందాం.
గణిత క్విజ్ లో పాల్గొన్న విద్యార్థులు = 10
x + y = 10 …………. (1)
గణిత క్విజ్ లో బాలికల సంఖ్య బాలుర సంఖ్య కన్నా 4 ఎక్కువ,
∴ x = y + 4
x – y = 4 …………. (2)

x + y = 10
y = 10 – x

x – y = 4
– y = 4 – x
y = x – 4

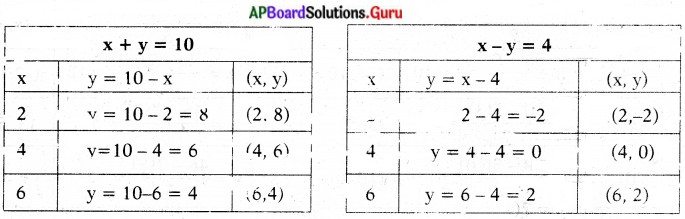
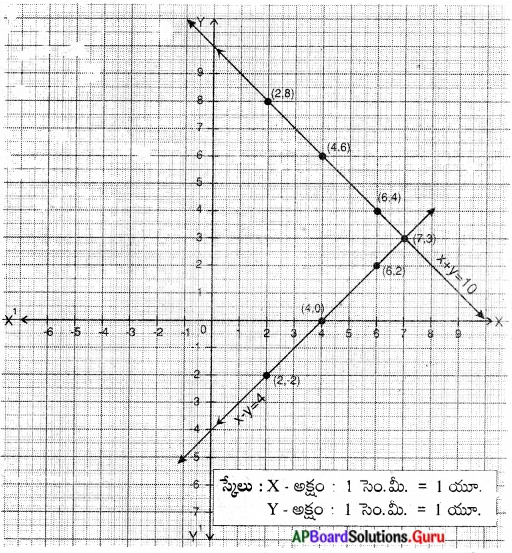
(x, y) = (7, 3)
∴ బాలికల సంఖ్య = 7
బాలుర సంఖ్య = 3.

ప్రశ్న 5.
5 పెన్సిళ్ళు మరియు 7 కలముల మొత్తము వెల ₹ 50. అలాగే 7 పెన్సిళ్ళు మరియు 5 కలముల మొత్తము వెల (అవే రకం) ₹ 46 అయిన ప్రతీ పెన్సిల్ మరియు కలముల వెల కనుగొనండి.
సాధన.
ఒక పెన్సిళ్ళు ₹ x, కలము వెల = ₹y అనుకుందాము.
5 పెన్సిళ్ళు మరియు 7 కలముల మొత్తం వెల ₹ 50
5 x + 7y = 50 ………….. (1)
7 పెన్సిళ్ళు మరియు 5 కలముల మొత్తం వెల ₹ 46
7x + 5y = 46 …………… (2)
5x + 7y = 50
7y = 50 – 5x
y = \(\frac{50-5 x}{7}\)

7x + 5y = 46
5y = 46 -7x
y = \(\frac{46-7 x}{5}\)

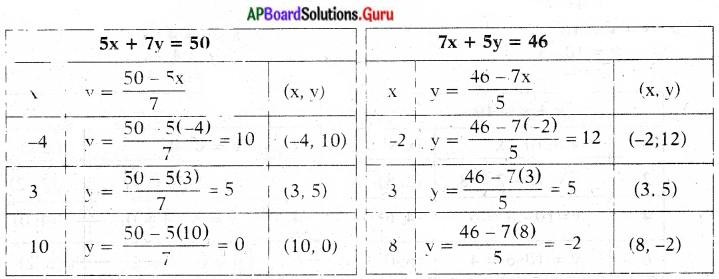
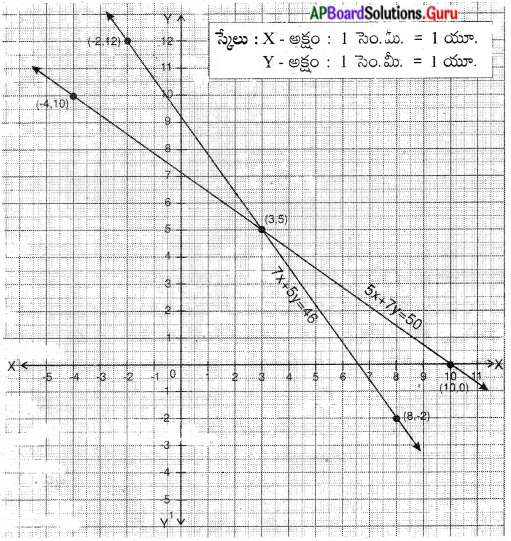
(x, y) = (3, 5)
ఒక పెన్సిల్ వెల = ₹ 3
ఒక కలము వెల = ₹ 5.

ప్రశ్న 6.
వెడల్పు కన్నా పొడవు 4 మీ. ఎక్కువ కలిగిన ఒక దీర్ఘచతురస్రాకార తోట చుట్టుకొలతలో సగము 36మీ. అయిన ఆ తోట కొలతలు కనుగొనుము.
సాధన.
దీర్ఘచతురస్ర పొడవు = 1 మీ., వెడల్పు = b మీ. అనుకుందాం
దీర్ఘచతురస్ర వెడల్పు కన్నా పొడవు 4 మీ. ఎక్కువ.
l = b + 4 ⇒ l – b = 4 ………… (1)
దీర్ఘచతురస్రాకార తోట చుట్టుకొలతలో సగము 36 మీ
\(\frac{2(l+b)}{2}\) ⇒ l + b = 36 ………… (2)
l – b = 4
– b = 4 – l
b = l – 4

l + b = 36
b = 36 – l

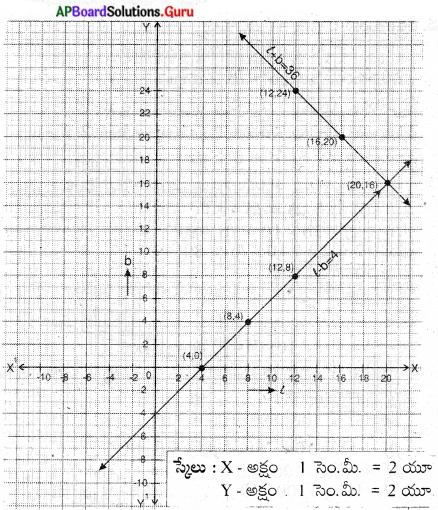
(l ,b) = (20, 16)
దీర్ఘచతురస్ర పొడవు = 20 మీ
వెడల్పు = 16 మీ

ప్రశ్న 7.
2x + 3y – 8 = 0 ఒక రేఖీయ సమీకరణము. దీనితో జ్యా మితీయంగా ఖండనరేఖలను ఏర్పరిచేటట్లు వేరొక రేఖీయ సమీకరణాన్ని రాయండి. అదేవిధంగా సమాంతర రేఖలు అయ్యేటట్లు, ఏకీభవించే రేఖలు. అయ్యేటట్లు మరి రెండు సమీకరణాలను రాయండి.
సాధన.
i) 2x + 3y – 8 = 0 కు ఖండనరేఖ అయ్యేటట్లుండే వేరొక రేఖీయ సమీకరణం 5x + 4y – 14 = 0.
(గమనిక : \(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) అయ్యేటట్లు ఉండే రేఖీయ సమీకరణాలు ఖండన రేఖలు అవుతాయి.)

ii) 2x + 3y – 8 = 0కు సమాంతరంగా ఉండే మరో రెండు సమీకరణాలు
i) 4x + 6y – 10 = 0 ii) 6x + 9y – 15 = 0
(గమనిక : \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\) అయితే రేఖీయ సమీకరణాలు సమాంతర రేఖలు అవుతాయి.)

iii) 2x + 3y – 8 = 0 తో ఏకీభవించే రేఖీయ సమీకరణాలు 4x + 6y – 16 = 0, 6x + 9y – 24 = 0
(గమనిక : \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) అయితే రేఖీయ సమీకరణాలు ఏకీభవిస్తాయి. (లేదా)
L₁, L₂ రేఖలు ఏకీభవించే రేఖలు అయితే రేఖీయ సమీకరణాలు L₂ = KL₁ KE R అయ్యేటట్లుంటాయి.
L₂ = 2x + 3y – 8 = 0 తో ఏకీభవించే రేఖీయ సమీకరణాలు L₂ = K (2x + 3y — 8) = 0, K యొక్క వివిధ విలువలకు వివిధ రేఖీయ సమీకరణాలు వస్తాయి.
K = 2 = L₂ = 4x + 6y – 16 = 0
K = 3 = L₂ = 6x + 9y – 24 = 0

ప్రశ్న 8.
ఒక దీర్ఘ చతురస్రానికి పొడవు 5 యూనిట్లు తగ్గించి, వెడల్పు 2 యూనిట్లు పెంచగా, వైశాల్యము 80 చదరపు యూనిట్లు తగ్గును. పొడవును 10 యూనిట్లు పెంచి, వెడల్పు 5 యూనిట్లు తగ్గించగా, వైశాల్యము 50 చదరపు యూనిట్లు పెరుగును. అయిన ఆ దీర్ఘ చతురస్రము పొడవు, వెడల్పులను కనుగొనుము.
సాధన.
దీర్ఘచతురస్ర పొడవు = l యూనిట్లు
వెడల్పు = b యూనిట్లు అనుకుందాం.
∴ దీర్ఘచతురస్ర వైశాల్యం = lb చ.యూ.
దీర్ఘచతురస్ర పొడవు 5 యూనిట్లు తగ్గించిన కొత్త పొడవు = l – 5 యూసట్లు
వెడల్పు 2 యూనిట్లు పెంచగా కొత్త వెడల్పు = b + 2 యూనిట్లు
వైశాల్యం = (l – 5) (b + 2) చ|| మీ.
పొడవు 5 యూనిట్లు తగ్గించి, వెడల్పు 2 యూనిట్లు పెంచగా వైశాల్యము 80 చ||యూ|| తగ్గును.
∴ (l – 5) (b + 2) = lb – 80.
lb + 2l – 5b – 10 = lb – 80.
lb + 2l – 5b – 10 – lb + 80 = 0
2l – 5b + 70 = 0 . ………….. (1)
దీర్ఘచతురస్ర పొడవు 10 యూనిట్లు పెంచిన కొత్త పొడవు = (l + 10) యూనిట్లు
వెడల్పు 5 యూనిట్లు తగ్గించిన కొత్త వెడల్పు = b – 5 యూనిట్లు
వైశాల్యము = (l – 10) (b – 5) చ|| యూనిట్లు
పొడవు 10 యూనిట్లు పెంచి, వెడల్పు 5 యూనిట్లు తగ్గించగా వైశాల్యం 500 చదరపు యూనిట్లు
(l + 10) (b – 5) = lb + 50
lb – 5l + 10b – 50 = lb + 50
lb – 5l + 10b – 50 – lb – 50 = 0
– 5l + 10b – 100 = 0
5l – 10b + 100 = 0 …………… (2)
2l – 5 b + 70 = 0
– 5 b = – 2l – 70
5 b = 2l + 70
b = \(\frac{2 l+70}{5}\)

5l – 10 b + 100 = 0
– 10 b = – 5l – 100
10 b = 5l + 100
b = \(\frac{5 l+100}{10}\)

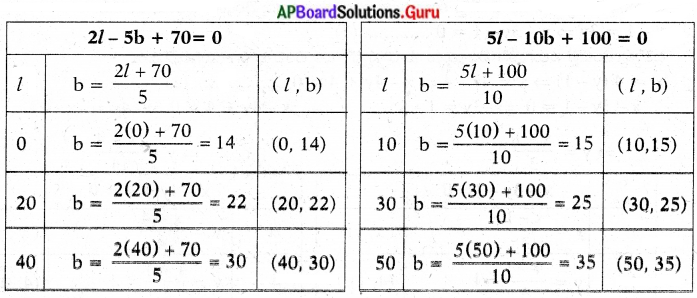
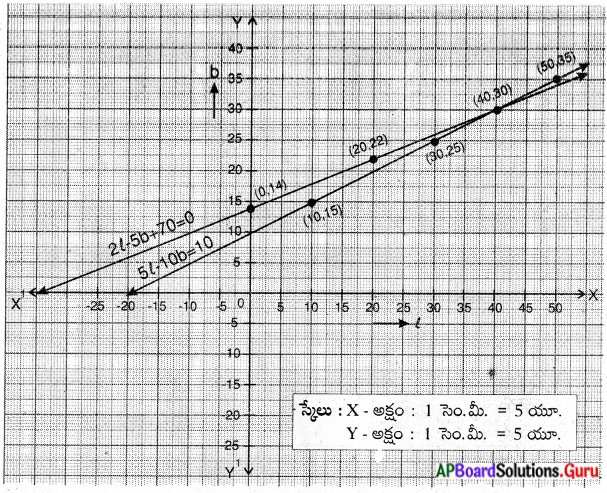
(l, b) = (40, 30)
దీర్ఘచతురస్ర పొడవు = 40 మీ.
వెడల్పు = 30 మీ

ప్రశ్న 9.
10వ తరగతిలో ముగ్గురేసి విద్యార్థులు ఒక బెంచిపై కూర్చొనగా, ఒక విద్యార్థికి కూర్చునేందుకు స్థలము ఉండదు. అలాగని ఒక్కొక్క బెంచిపై నలుగురేసి విద్యార్థులు కూర్చొన్నచో, ఒక బెంచి ఖాళీగా మిగిలిపోవును. అయిన ఆ తరగతిలోని విద్యార్థులెందరు ? బెంచీలెన్ని ? కనుగొనుము.
సాధన.
తరగతిలోని విద్యార్థుల సంఖ్య = x, బెంచీల సంఖ్య = y అనుకుందాం.
ముగ్గురేసి విద్యార్థులు ఒక బెంచి పై కూర్చొనగా ఒక విద్యార్థి కూర్చునేందుకు స్థలము ఉండదు.
x – 1 = 3y ⇒ x – 3y – 1 = 0 …………. (1)
ఒక్కొక్క బెంచి పై నలుగురేసి విద్యార్థులు కూర్చొన్నచో, ఒక బెంచి ఖాళీగా మిగిలిపోవును.
x = 4 (y – 1) ⇒ x = 4y – 4 ⇒ x – 4y + 4 = 0 ……… (2)
x – 3y – 1 = 0 ⇒ – 3y = 1 – x
⇒ y = \(\frac{x-1}{3}\)

x – 4y + 4 = 0 ⇒ – 4y = – x – 4
⇒ y = \(\frac{x+4}{4}\)

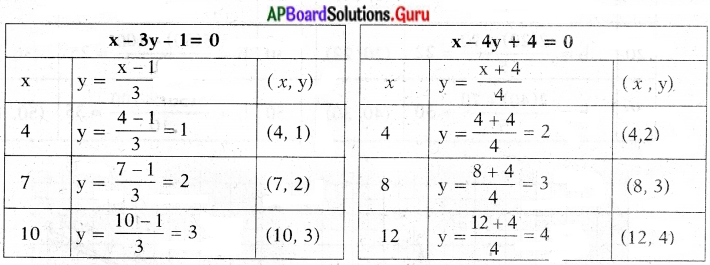
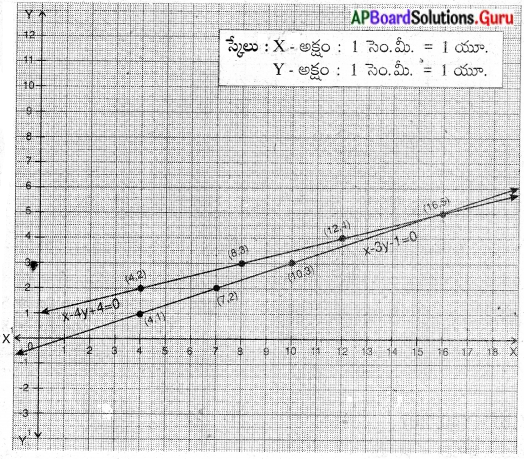
∴ ( x, y) = (16, 5)
తరగతిలోని విద్యార్థుల సంఖ్య = 16
బెంచీల సంఖ్య = 5