SCERT AP 10th Class Maths Textbook Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.3 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Exercise 4.3
ప్రశ్న 1.
క్రింది సమీకరణాల జతలను, రేఖీయ సమీకరణాల ‘ జతలుగా మార్చడం ద్వారా వాటికి సాధన కనుగొనండి.
(i) \(\frac{5}{x-1}+\frac{1}{y-2}\) = 2
\(\frac{6}{x-1}-\frac{3}{y-2}\) = 1
సాధన.
\(\frac{5}{x-1}+\frac{1}{y-2}\) = 2 ……………(1)
\(\frac{6}{x-1}-\frac{3}{y-2}\) = 1 …………….(2)
(1) మరియు (2) లలో \(\frac{1}{x-1}\) = p \(\frac{`1}{y-2}\) = q అనుకొనుము.
(1) ⇒ 5p + q = 2 ………….. (3)
(2) ⇒ 6p – 3q = 1 ………….. (4)
(3) ⇒ q = 2 – 5p ని (4) లో ప్రతిక్షేపించగా,
6p – 3 (2 – 5p) = 1
6p – 6 + 15p = 1
21p = 1 + 6 = 7
⇒ p = \(\frac{7}{21}\) = \(\frac{1}{3}\)
p = \(\frac{1}{3}\) ని (4) లో రాయగా,
6 (\(\frac{1}{3}\)) – 3q = 1
– 3q = 1 – 2 = – 1
⇒ 3q = 1
⇒ q = \(\frac{1}{3}\)
p = \(\frac{1}{3}\), q = \(\frac{1}{3}\)
కానీ \(\frac{1}{x-1}\) = p = \(\frac{1}{3}\)
x – 1 = 3 ⇒ x = 3 + 1 = 4 1
\(\frac{1}{y-2}\) = q = \(\frac{1}{3}\)
y – 2 = 3 ⇒ y = 3 + 2 = 5
∴ సాధన x = 4, y = 5.
సరిచూచుట :
\(\frac{5}{x-1}+\frac{1}{y-2}\) = 2
x = 4, y = 5 విలువలను రాయగా,
\(\frac{5}{4-1}+\frac{1}{5-2}\) = 2
\(\frac{5}{x-1}+\frac{1}{y-2}\)
\(\frac{5}{3}+\frac{1}{3}\) = 2
⇒ \(\frac{6}{3}\) = 2
⇒ 2 = 2
![]()
(ii) \(\frac{x+y}{x y}\) = 2;
\(\frac{x-y}{x y}\) = 6
సాధన.
\(\frac{x+y}{x y}\) = 2 ………….(1)
\(\frac{x-y}{x y}\) = 6 …………(2)
(1) ⇒ \(\frac{x}{x y}+\frac{y}{x y}\) = 2
\(\frac{1}{y}+\frac{1}{x}\) = 2
(2) ⇒ \(\frac{x}{x y}-\frac{y}{x y}\) = 6
\(\frac{1}{y}-\frac{1}{x}\) = 6 ……………(4)
\(\frac{1}{x}\) = q, \(\frac{1}{y}\) = p అనుకుంటే,
(3) ⇒ p + q = 2 ………….. (5)
(4) ⇒ p – q = 6 ………….. (6)
p + q = 2
p – q = 6
(5) + (6) ⇒ 2p = 8
⇒ p = \(\frac{8}{2}\) = 4
p = 4 ను (5) లో రా యగా,
4 + q = 2
⇒ q = 2 – 4 = – 2
p = 4, q = – 2
కానీ, \(\frac{1}{y}\) = p = 4
y = \(\frac{1}{4}\)
⇒ q = – 2 ⇒ x = – \(\frac{1}{2}\)
∴ సాధన x = – \(\frac{1}{2}\) , y = \(\frac{1}{4}\)
సరిచూచుట :
\(\frac{x+y}{x y}\) = 2
x, y విలువలను రాయగా, \(\frac{-\frac{1}{2}+\frac{1}{4}}{\frac{-1}{2} \times \frac{1}{4}}\) = 2

![]()
(iii) \(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}\) = 2
\(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}\) = – 1
సాధన.
\(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}\) = 2 ………….(1)
\(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}\) = – 1 ………….(2)
\(\frac{1}{\sqrt{x}}\) = p, \(\frac{1}{\sqrt{y}}\) = q అనుకుంటే,
(1) ⇒ 2p + 3q = 2 ………….. (3)
(2) ⇒ 4p – 9q = – 1 …………. (4)
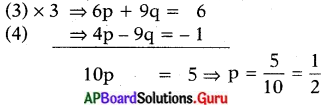
p = \(\frac{1}{2}\) ను (3) లో రాయగా,
2(\(\frac{1}{2}\)) + 3q = 2
3q = 2 -1 = 1
⇒ q = \(\frac{1}{3}\)
కానీ \(\frac{1}{\sqrt{x}}\) = p = \(\frac{1}{2}\)
⇒ √x = 2
⇒ x = 4
\(\frac{1}{\sqrt{y}}\) = q = \(\frac{1}{3}\)
⇒ √y = 3
⇒ y = 9
∴ సాధన x = 4, y = 9.
సరిచూచుట :
x, y విలువలను (1) లో రాయగా, \(\frac{2}{\sqrt{4}}+\frac{3}{\sqrt{9}}\) = 2
⇒ \(\frac{2}{2}+\frac{3}{3}\) = 2
⇒ 1 + 1 = 2
⇒ 2 = 2
![]()
(iv) 6x + 3y = 6xy
2x + 4y = 5xy
సాధన.
6x + 3y = 6xy ……….. (1)
2x + 4y = 5x………… (2)
(1) ⇒ \(\frac{6 x}{x y}+\frac{3 y}{x y}\) = 6 (∵ ఇరువైపులా xy తో భాగించగా)
\(\frac{6}{y}+\frac{3}{x}\) = 6 ………..(3)
(2) ⇒ \(\frac{2 x}{x y}+\frac{4 y}{x y}\) = 5
\(\frac{2}{y}+\frac{4}{x}\) = 5 …………….(4)
\(\frac{1}{y}\) = P, \(\frac{1}{x}\) = q అనుకుందాం.
(3) ⇒ 6p + 3q = 6 …………. (5)
⇒ 2p + 4q = 5 ………….. (6)
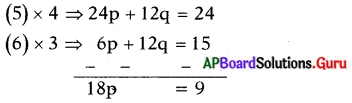
p = \(\frac{9}{18}=\frac{1}{2}\)
p = \(\frac{1}{2}\) ను (5) లో ప్రతిక్షేపించగా,
6(\(\frac{1}{2}\)) + 3q = 6
3q = 6 – 3
q = \(\frac{3}{3}\) = 1
కానీ \(\frac{1}{y}\) = p = \(\frac{1}{2}\)
⇒ y = 2
\(\frac{1}{x}\) = q = 1
⇒ x = 1
∴ సాధన x = 1, y = 2.
సరిచూచుట :
x, y విలువలను (1) లో రాయగా,
6 (1) + 3 (2) = 6 (1) (2)
6 + 6 = 12
12 = 12
![]()
(v) \(\frac{5}{x+y}-\frac{2}{x-y}\) = – 1
\(\frac{15}{x+y}+\frac{7}{x-y}\) = 10 x ≠ 0, y ≠ 0 అయిన
సాధన.
\(\frac{5}{x+y}-\frac{2}{x-y}\) = – 1 …………… (1)
\(\frac{15}{x+y}+\frac{7}{x-y}\) = 10 …………. (2)
\(\frac{1}{x+y}\) = p, \(\frac{1}{x-y}\) = q అనుకుంటే,
(1) ⇒ 5p – 2q = – 1 …………. (3)
(2) ⇒ 15p + 7q = 10 ………. (4)

p = \(\frac{1}{5}\) ను (3) లో రాయగా,
5(\(\frac{4}{4}\)) – 2q = – 1
1 – 2q = -1
– 2q = – 1 – 1
2q = 2
q = \(\frac{2}{2}\) = 1
p = \(\frac{1}{5}\), q = 1
కానీ, \(\frac{1}{x+y}\) = P = \(\frac{1}{5}\)
⇒ x + y = 5 ………… (5)
\(\frac{1}{x-y}\) = q = 1
⇒ x – y = 1 …… (6)
(5) మరియు (6) లను సాధించగా,
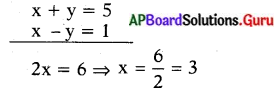
x = 3ను (5) లో రాయగా,
3 + y = 5
y = 5 – 3 = 2
∴ సాధన x = 3, y = 2.
సరిచూచుట :
x, y విలువలను (2) లో రాయగా,
\(\frac{15}{3+2}+\frac{7}{3-2}\) = 10
\(\frac{15}{5}+\frac{7}{1}\) = 10
3 + 7 = 10
10 = 10
![]()
(vi) \(\frac{2}{x}+\frac{3}{y}\) = 13
\(\frac{5}{x}-\frac{4}{y}\) = – 2 x ≠ 0, y ≠ 0 అయిన
సాధన.
\(\frac{2}{x}+\frac{3}{y}\) = 13 …………… (1)
\(\frac{5}{x}-\frac{4}{y}\) = – 2 …………… (2)
\(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q అనుకుంటే,
(1) ⇒ 2p+ 3q = 13 ………….(3)
(2) ⇒ 5p – 4q = – 2 ………..(4)

p = 2 ను (3) లో రాయగా,
2(2) + 3q = 13
4 + 3q = 13
3q = 13 – 4 = 9
⇒ q = \(\frac{9}{3}\) = 3
p = 2, q = 3
కానీ, \(\frac{1}{x}\) = p = 2
⇒ x = \(\frac{1}{2}\)
\(\frac{1}{y}\) = q = 3
⇒ y = \(\frac{1}{3}\)
∴సాధన x = \(\frac{1}{2}\), y = \(\frac{1}{3}\)
సరిచూచుట :
x, y విలువలను (1) లో ప్రతిక్షేపించగా,
\(\frac{2}{\frac{1}{2}}+\frac{3}{\frac{1}{3}}\) = 13
⇒ 2 × \(\frac{2}{1}\) + 3 × \(\frac{3}{1}\) = 13
⇒ 4 + 9 = 13
⇒ 13 = 13
![]()
(vii) \(\frac{10}{x+y}+\frac{2}{x-y}\) = 4
\(\frac{15}{x+y}-\frac{5}{x-y}\) = – 2
సాధన.
\(\frac{10}{x+y}+\frac{2}{x-y}\) = 4 ………. (1)
\(\frac{15}{x+y}-\frac{5}{x-y}\) = – 2 ………….. (2)
\(\frac{1}{x+y}\) = p, \(\frac{1}{x-y}\) = q అనుకుంటే,
(1) ⇒ 10p + 2q = 4 ………….. (3)
(2) ⇒ 15p – 5q = – 2…………… (4)

p = \(\frac{1}{5}\) ను (3) లో రాయగా,
10(\(\frac{1}{5}\)) + 2q = 4
2 + 2q = 4
⇒ 2q = 4 – 2
⇒ 2q = 2
q = \(\frac{2}{2}\) = 1, p = \(\frac{1}{5}\), q = 1
కానీ, \(\frac{1}{x+y}\) = p = \(\frac{1}{5}\)
⇒ x + y = 5 …………….. (5)
\(\frac{1}{x+y}\) = q = 1
⇒ x – y = 1 …………….. (6)
(5), (6) లను సాధించగా,

x = 3 ను (5) లో రాయగా,
3 + y = 5
⇒ y = 5 – 3 = 2
∴ సాధన, x = 3, y = 2.
సరిచూచుట :
x, y విలువలను (1) లో ప్రతిక్షేపించగా,
\(\frac{10}{3+2}+\frac{2}{3-2}\) = 4
⇒ \(\frac{10}{5}+\frac{2}{1}\) = 4
2 + 2 = 4
4 = 4
![]()
(viii) \(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\)
\(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=\frac{-1}{8}\)
సాధన.
\(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\) …………….(1)
\(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=\frac{-1}{8}\) ………. (2)
(2) ⇒ \(\frac{1}{2}\left[\frac{1}{3 x+y}-\frac{1}{3 x-y}\right]=\frac{-1}{8}\)
⇒ \(\frac{1}{3 x+y}-\frac{1}{3 x-y}=\frac{-2}{8}\)
⇒ \(\frac{1}{3 x+y}-\frac{1}{3 x-y}=\frac{-1}{4}\) ………………(3)
(1) & (3) లలో \(\frac{1}{3 x+y}\) = p, \(\frac{1}{3 x-y}\) = q అనుకుంటే,
(1) ⇒ p + q = \(\frac{3}{4}\) …………. (4)
(3) ⇒ p – q = \(\frac{1}{4}\) ……….. (5)
(4) + (5) ⇒

p = \(\frac{1}{4}\) ను (4) లో రాయగా,
\(\frac{1}{4}\) + q = \(\frac{3}{4}\)
q = \(\frac{3}{4}\) – \(\frac{1}{4}\)
= \(\frac{3-1}{4}=\frac{2}{4}=\frac{1}{2}\)
p = \(\frac{1}{4}\), q = \(\frac{1}{2}\)
కానీ, \(\frac{1}{3 x+y}\) = p = \(\frac{1}{4}\)
⇒ 3x + y = 4 …………(6)
\(\frac{1}{3 x-y}\) = q = \(\frac{1}{2}\)
⇒ 3x – y = 2 ……. (7)
(6), (7) లను సాధించగా.
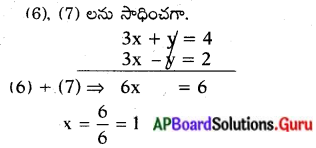
x = 1 ని (6) లో రా యగా,
3 (1) + y = 4 ⇒ y = 4 – 3 = 1
సాధన x = 1, y = 1.
సరిచూచుట :
x, y విలువలను (1) లో ప్రతిక్షేపించగా,
\(\frac{1}{3(1)+1}+\frac{1}{3(1)-1}=\frac{3}{4}\)
![]()
ప్రశ్న 2.
క్రింది సమస్యలకు సమీకరణాల జతలను వ్రాసి వాటికి సాధన కనుగొనండి.
(i) ఒక పడవ నీటిలో ప్రవాహమునకు అభిముఖముగా 30 కి.మీ దూరమును మరియు ప్రవాహపువాలులో 44 కి.మీ. దూరము ప్రయాణించుటకు 10 గంటలు పట్టును. అదే పడవకు 40 కి.మీ అభిముఖముగా, 55 కి.మీ. ప్రవాహపు వాలులో ప్రయాణించుటకు 13 గంటలు కాలము పట్టును. అయిన ప్రవాహవేగమును, నిలకడ నీటిలో పడవ వేగమును కనుగొనుము.
సాధన.
నిలకడ నీటిలో పడవ వేగం = x కి.మీ./గం.
ప్రవాహ వేగము = y కి.మీ./ గం. అనుకొనుము
ప్రవాహ అభిముఖంగా పడవ వేగం = (x – y) కి.మీ./గం.
ప్రవాహవాలు (ప్రవాహ దిశలో) గా పడవవేగం = (x + y) కి.మీ./గం. దూరం

సందర్భం -1:
ప్రవాహ అభిముఖంగా 30 కి.మీ. ప్రయాణానికి పట్టే కాలం = \(\frac{30}{x-y}\) గం.
ప్రవాహవాలుగా 44 కి.మీ. ప్రయాణించుటకు పట్టే 44 కాలం = \(\frac{44}{x+y}\) గం.
మొత్తం ప్రయాణానికి పట్టిన కాలం = 10 గం.
\(\frac{30}{x-y}+\frac{44}{x+y}\) = 10 …… (1)
సందర్భం – 2:
ప్రవాహ అభిముఖంగా 40 కి.మీ. ప్రయాణించుటకు పట్టే కాలం = \(\frac{40}{x-y}\) గం
ప్రవాహ వాలులో 55 కి.మీ. ప్రయాణించుటకు పట్టే కాలం = \(\frac{55}{x+y}\) గం.
మొత్తం ప్రయాణానికి పట్టిన కాలం = 13 గం.
\(\frac{40}{x-y}+\frac{55}{x+y}\) = 13 ……….. (2)
\(\frac{1}{x-y}\) = p మరియు \(\frac{1}{x+y}\) = q అనుకొంటే
(1) ⇒ 30p + 44q = 10 ………… (3)
(2) ⇒ 40p + 55q = 13 ………… (4)
30, 40 ల క.సా.గు = 120,

q = \(\frac{1}{11}\)
q = \(\frac{1}{11}\) ని (3) లో రాయగా
30p + 44 (\(\frac{1}{11}\)) = 10
30p + 4 = 10
30p = 10 – 4 = 6
⇒ p = \(\frac{6}{30}=\frac{1}{5}\)
కానీ, \(\frac{1}{x-y}\) = p = \(\frac{1}{5}\)
⇒ x – y = 5 ……………..(5)
\(\frac{1}{x+y}\) = q = \(\frac{1}{11}\)
⇒ x + y =11 ……………….(6)
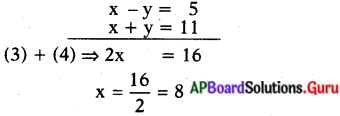
x = 8ని (6) లో రాయగా,
8 + y = 11
y = 11 – 8 = 3
∴ సాధన x = 8, y = 3.
నిలకడ నీటిలో పడవ వేగం = 8 కి. మీ./గం,
ప్రవాహ వేగము = 3 కి. మీ./గం.
సరిచూచుట :
అభిముఖంగా 30 కి.మీ. ప్రయాణానికి పట్టే కాలము = \(\frac{30}{8-3}=\frac{30}{5}\) = 6 గం.
ప్రవాహవాలుగా 40 కి.మీ. ప్రయాణానికి పట్టే కాలం = \(\frac{40}{8+2}=\frac{40}{10}\) = 4 గం.
మొత్తం ప్రయాణకాలం = 6 + 4 = 10 గం.
![]()
(ii) రహీమ్ తన యింటికి పోవుటకు 600 కి.మీ దూరములో, కొంత దూరము రైలులో మరియు కొంత దూరము కారులో ప్రయాణించును. 120 కి.మీ. దూరము రైలులో, మిగిలిన దూరము కారులో ప్రయాణమునకు అతనికి 8 గంటలు పట్టును. అదే 200కి.మీ. దూరము రైలులో, మిగిలిన దూరము కారులో ప్రయాణము చేసిన అతనికి 20 నిమిషాల కాలము ఎక్కువ పట్టును. అయిన కారు మరియు రైలుల వేగములను కనుగొనండి. సాధన.
రైలు వేగము = x కి.మీ./గం.
కారు వేగము = y కి.మీ./గం. అనుకుందాం.
సందర్భం – 1:
120 కి.మీ. రైలు ప్రయాణానికి పట్టిన కాలం = \(\frac{120}{x}\) గం
600 – 120 = 480 కి.మీ. ‘కారు ప్రయాణానికి
పట్టిన కాలం = \(\frac{480}{y}\) గం
మొత్తం ప్రయాణకాలం = 8 గం.
\(\frac{120}{x}+\frac{480}{y}\) = 8 …………….. (1)
సందర్భం – 2:
200 కి.మీ. రైలు ప్రయాణానికి పట్టిన కాలం = \(\frac{200}{x}\) గం.
600 – 200 = 400 కి.మీ. కారు ప్రయాణానికి పట్టిన కాలం = \(\frac{400}{y}\) గం.
మొత్తం ప్రయాణ కాలం = 8 గం. + 20 ని.
\(\frac{200}{x}+\frac{400}{y}=8 \frac{20}{60}\) గం. = \(\frac{25}{3}\) గం.
∴ \(\frac{200}{x}+\frac{400}{y}=\frac{25}{3}\) …………….(2)
\(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q అనుకుంటే,
(1) ⇒ 120p + 480q = 8 ………………… (3)
(2) ⇒ 200p + 400q = \(\frac{25}{3}\) ……………. (4)

q = \(\frac{1}{80}\) = ని (3) లో రాయగా,
120p + 480(\(\frac{1}{80}\)) = 8
⇒ 120p = 8 – 6 = 2
⇒ p = \(\frac{2}{120}\)
⇒ p = \(\frac{1}{60}\)
∴ p = \(\frac{1}{60}\), q = \(\frac{1}{80}\)
కానీ, \(\frac{1}{x}\) = p = \(\frac{1}{60}\)
⇒ x = 60
\(\frac{1}{y}\) = q = \(\frac{1}{80}\)
⇒ y = 80
∴ సాధన x = 60, y = 80.
రైలు వేగం = 60 కి.మీ./గం.
కారు వేగం = 80 కి.మీ./గం.
సరిచూచుట :
120 కి.మీ. రైలు ప్రయాణానికి పట్టే కాలం = \(\frac{120}{60}\) = 2 గం.
480 కి.మీ. కారు ప్రయాణానికి పట్టే కాలం = \(\frac{480}{80}\) = 6 గం.
![]()
మొత్తం ప్రయాణకాలం = 2 + 6 = 8 గం.
(iii) ఇద్దరు స్త్రీలు మరియు 5గురు పురుషులు ఒక కుట్టుపనిని 4 రోజులలో చేయగా, ముగ్గురు స్త్రీలు మరియు 6గురు పురుషులు దానిని 3 రోజులలో చేసెదరు. స్త్రీ ఒక్కరే లేదా పురుషుడు ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలమును కనుగొనుము.
సాధన.
స్త్రీ ఒక్కరే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలం = x రోజులు
పురుషుడు ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలం = y రోజులు అనుకుందాం.
స్త్రీ ఒక్కరే 1 రోజు చేయు పని = \(\frac{1}{x}\)
పురుషుడు ఒక్కడే 1 రోజు చేయు పని = \(\frac{1}{y}\)
సందర్భం -1:
ఇద్దరు స్త్రీలు మరియు 5 గురు పురుషులు ఆ పనిని 4 రోజులలో చేయుదురు.
కావున, ఇద్దరు స్త్రీలు మరియు 5 గురు పురుషులు ఒక రోజులో చేయు పని = \(\frac{1}{4}\)
∴ \(\frac{2}{x}+\frac{5}{y}=\frac{1}{4}\)
[∵ ఇద్దరు స్త్రీలు ఒకరోజులో చేయు పని = 2 × \(\frac{1}{x}\) = \(\frac{2}{x}\)
5 గురు పురుషులు ఒక రోజులో చేయు పని = 5 × \(\frac{1}{y}\) = \(\frac{5}{y}\)]
∴ \(\frac{8}{x}+\frac{20}{y}\) = 1 ……………. (1)
సందర్భం – 2:
ముగ్గురు స్త్రీలు మరియు 6 గురు పురుషులు ఆ పనిని 3 రోజులలో చేసెదరు.
∴ ముగ్గురు స్త్రీలు మరియు 6 గురు పురుషులు ఒక రోజు చేయు పని = \(\frac{1}{3}\)
\(\frac{3}{x}+\frac{6}{y}=\frac{1}{3}\)
⇒ \(\frac{9}{x}+\frac{18}{y}\) = 1 ………… (2)
p = \(\frac{1}{x}\), q = \(\frac{1}{y}\) అనుకుంటే,
(1) ⇒ 8p + 20q = 1 ………….. (3)
(2) ⇒ 9p + 18q = 1 ………….. (4)

q = \(\frac{1}{36}\) ను (4) లో రాయగా,
9p + 18(\(\frac{1}{36}\)) = 1
⇒ 9p + \(\frac{1}{2}\) = 1
⇒ 9p = 1 – \(\frac{1}{2}\) = \(\frac{1}{2}\)
⇒ p = \(\frac{1}{18}\)
⇒ p = \(\frac{1}{18}\), q = \(\frac{1}{36}\)
కానీ \(\frac{1}{x}\) = p = \(\frac{1}{18}\)
⇒ x = 18
\(\frac{1}{y}\) = q = \(\frac{1}{36}\)
⇒ y = 36
‘స్త్రీ ఒక్కరే ఆ పని పూర్తి చేయుటకు పట్టు కాలం = 18 రోజులు
‘పురుషుడు ఒక్కరే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలం = 36 రోజులు.
సరిచూచుట :
x = 18, y = 36 ని (2) లో రాయగా,
\(\frac{9}{18}+\frac{18}{36}\) = 1
⇒ \(\frac{1}{2}+\frac{1}{2}\) = 1
⇒ \(\frac{2}{2}\) = 1