AP Board 10th Class Maths Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Optional Exercise

SCERT AP 10th Class Maths Textbook Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Optional Exercise Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత Optional Exercise

ప్రశ్న 1.
క్రింది సమీకరణాలను సాధించండి :
(i) \(\frac{2 x}{a}+\frac{y}{b}\) = 2;
\(\frac{x}{a}-\frac{y}{b}\) = 4
సాధన.
1వ పద్ధతి :
\(\frac{2 x}{a}+\frac{y}{b}\) = 2 …………….. (1);
\(\frac{x}{a}-\frac{y}{b}\) = 4……………….. (2)

x = 2a ని (2) లో రాయగా,
\(\frac{2 a}{a}-\frac{y}{b}\) = 4
⇒ – \(\frac{y}{b}\) = 4 – 2
⇒ – \(\frac{y}{b}\) = 2 =
⇒ – y = 2b
∴ y = – 2b
సాధన x= 2a, y = – 2b.

2వ పద్ధతి :
(1) ⇒ \(\frac{y}{b}\) = 2 – \(\frac{2 x}{a}\) (2) లో ప్రతిక్షేపించగా
\(\frac{x}{a}\) – (2 – \(\frac{2 x}{a}\))
⇒ \(\frac{x}{a}\) – 2 + \(\frac{2 x}{a}\) – 4
⇒ \(\frac{3 x}{a}\) = 4 + 2 = 6
⇒ x = 6 × \(\frac{a}{3}\) = 2a
x = 2a ను (2) లో రాయగా,
\(\frac{2 a}{a}\) – \(\frac{y}{b}\) = 4
⇒ – \(\frac{y}{b}\) = 4
2 = 2
⇒ – y = 2b
y = – 2b
సాధన x = 2a, y = – 2b

3వ పద్ధతి :
\(\frac{2 x}{a}+\frac{y}{b}\) = 2 …………….. (1)

\(\frac{x}{a}-\frac{y}{b}\) = 4 …………….. (2)

(1) ⇒ \(\frac{2 b x+a y}{a b}\) = 2
⇒ 2bx + ay = 2ab ………… (3)
(2) ⇒ \(\frac{b x-a y}{a b}\) = 4
⇒ bx – ay = 4ab …………..(4)

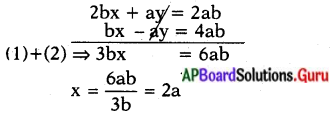
x = 2a ని (3) లో రా3యగా,
2b (2a) + ay = 2ab
⇒ 4ab + ay = 2ab
⇒ ay = 2ab – 4ab = – 2ab
y = \(\frac{-2 \mathrm{ab}}{\mathrm{a}}\) = – 2b
సాధన x = 2a, y = 2b

సరిచూచుట :
x = 2a, y = – 2b ని (2) లో రాయగా
\(\frac{-2 \not a}{\not a}\) – (- \(\frac{-2 \not b}{\not b}\)) = 4
⇒ 2 + 2
⇒ 4= 4 = 4.

(ii) \(\frac{x+1}{2}+\frac{y-1}{3}\) = 8

\(\frac{x-1}{3}+\frac{y+1}{2}\) = 9
సాధన.
\(\frac{x+1}{2}+\frac{y-1}{3}\) = 8 ……………..(1)

\(\frac{x-1}{3}+\frac{y+1}{2}\) = 9 ……………..(2)
(1) ⇒ \(\frac{3(x+1)+2(y-1)}{6}\) = 8
3x + 3 + 2y – 2 = 48
3x + 2y = 48 – 10
3x + 2y = 47 …………… (4)
(2) ⇒ \(\frac{2(x-1)+3(y+1)}{6}\) = 9
2x – 2 + 3y + 3 = 54
2x + 3y = 54 – 15
2x + 3y = 53 …………… (4)

x = 7 ను (3) లో రాయగా,
3 (7) + 2y = 47
⇒ 2y = 47 – 21
⇒ 2y = 26
⇒ y = \(\frac{26}{2}\) = 13
సాధన x = 7, y = 13.

సరిచూచుట :
x, y విలువలను (1) లో రాయగా,
\(\frac{7+1}{2}+\frac{13-1}{3}\) = 8
\(\frac{8}{2}+\frac{12}{3}\) = 8
⇒ 4 + 4 = 8
⇒ 8 = 8.

(iii) \(\frac{x}{7}+\frac{y}{3}\) = 5;
\(\frac{x}{2}-\frac{y}{9}\) = 6
సాధన.
1వ పద్ధతి
\(\frac{x}{7}+\frac{y}{3}\) = 5 ……………(1)

\(\frac{x}{2}-\frac{y}{9}\) = 6 …………….(2)

(1) ⇒ \(\frac{3 x+7 y}{21}\) = 5
⇒ 3x + 7y = 105 …………….. (3)
\(\frac{9 x-2 y}{18}\) = 6
9x – 2y = 108 ………….. (4)

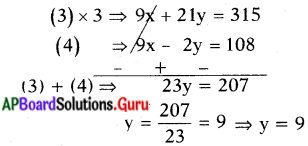
y = 9 ని (4) లో రాయగా
9x – 2(9) = 108
9x – 18 = 108
9x = 108 + 18 = 126
x = \(\frac{120}{9}\) = 14
సాధన x = 14, y = 9

2వ పద్దతి :
\(\frac{x}{7}+\frac{y}{3}\) = 5 …………..(1)

\(\frac{x}{2}-\frac{y}{9}\) …………… (2)

x = 14 ని (1) లో రాయగా

\(\frac{14}{7}+\frac{y}{3}\) = 5

⇒ 2 + \(\frac{y}{3}\) = 5
⇒ \(\frac{y}{3}\) = 5 – 2 = 3
⇒ y = 9 .
సాధన x = 14, y = 9.

సరిచూచుట :
x, y విలువలను (1) లో రాయగా,
\(\frac{14}{7}+\frac{9}{3}\) = 5
2 + 3 = 5
5 = 5

(iv) √3x – √2y = √3; √5x + √3y =√3
సాధన.
√3x – √2y = √3 …………. (1) .
√5x + √3y = √3 ……….. (2)
1వ పద్ధతి :
(1) ⇒ – √2y = √3 – √3x
√2y = √3x – √3
y = \(\frac{\sqrt{3} x-\sqrt{3}}{\sqrt{2}}\) ను (2) లో ప్రతిక్షేపించగా,

√5x + √3(\(\frac{\sqrt{3} x-\sqrt{3}}{\sqrt{2}}\)) = √3

√5x + \(\frac{3 x-3}{\sqrt{2}}\) = √3

\(\frac{\sqrt{10} x+3 x-3}{\sqrt{2}}\) = √3

x(√10 + 3) – 3 = √6
x(3 + √10) = 3 + √6
x = \(\frac{3+\sqrt{6}}{3+\sqrt{10}}\)
x విలువను (2) లో ప్రతిక్షేపించగా,
√5 (\(\)) + √3y = √3

\(\frac{3+\sqrt{6}}{3+\sqrt{10}}\) + √3y = √3

√3y = √3 – \(\frac{3 \sqrt{5}+\sqrt{30}}{3+\sqrt{10}}\)

2వ పద్ధతి:
√3x – √2y = √3 …………(1)
√5x + √3y = √3 ……….. (2)

x = \(\frac{3+\sqrt{6}}{3+\sqrt{10}}\)

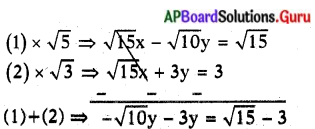
√10y + 3y = 3 – √15
y(3 + √10) = 3 – √15
⇒ y = \(\frac{3-\sqrt{15}}{3+\sqrt{10}}\)
∴ సాధన. x = \(\frac{3+\sqrt{6}}{3+\sqrt{10}}\) , y = \(\frac{3-\sqrt{15}}{3+\sqrt{10}}\).

(v) \(\frac{a x}{b}-\frac{b y}{a}\) = a + b; ax – by = 2ab
సాధన.
\(\frac{a x}{b}-\frac{b y}{a}\) = a +b; …………….(1)
ax – by = 2ab …….. (2)
(1) ⇒ \(\frac{a^{2} x-b^{2} y}{a b}\) = a + b
a²x – b²y = ab (a + b)
a²x – b²y = a²b + ab² ……….. (3)
(2) × b = abx – b²y = 2ab² …………… (4)

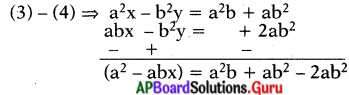
x = \(\frac{a^{2} b-a b^{2}}{a^{2}-a b}\)
⇒ x = \(\frac{a b(a-b)}{a(a-b)}\)
⇒ x = b
x = b ని (2) లో రాయగా
ab – by = 2ab
– by = 2ab – ab = ab
⇒ by = – ab
⇒ y = \(\frac{-a b}{b}\) = – a
⇒ y = – a

సరిచూడటం:
x, y విలువలను (2) లో రాయగా,
a(b) – b (- a) = 2ab
⇒ ab + ab = 2ab
⇒ 2ab = 2ab.

(vi) 2^x + 3^y = 17; 2^{x + 2} – 3^{y + 1} = 5
సాధన.
2^x + 3^y = 17 …………. (1)
2^{x + 2} – 3^{y + 1} = 5 ………… (2)
(2) ⇒ 2^x × 2² – 3^y × 3 = 5
(∵ a^{m + n} = a^m × aⁿ)
4 × 2^x – 3 × 3^y = 5 ………. (3)
(1) మరియు (3)లలో 2^x = p, 3^y = q అనుకొనుము.
(1) ⇒ p+ q = 17 ………. (4)
(3) ⇒ 4p- 3q = 5 ………. (5)
(4) ⇒ q= 17 – pని (5) లో ప్రతిక్షేపించగా,
4p – 3 (17 – p) = 5
4p -51 + 3p = 5
7p = 5 + 51 = 56
⇒ p = \(\frac{56}{7}\) = 8
p = 8ని (4) లో రాయగా,
8 + q = 17
⇒ q = 17 – 8 = 9
p = 8, q = 9
కాని, 2^x = p = 8
2^x = 2³
⇒ x = 3,
3^y = q = 9
3^y = 3²
⇒ y = 2
సాధన x = 3, y = 2.

సరిచూడటం :
x, y విలువలు (1) లో రాయగా,
2³ + 3² = 17
⇒ 8 + 9 = 17
⇒ 17 = 17

ప్రశ్న 2.
ఒక ప్రయోగంలో జంతువులకు నిర్దేశించిన ఆహారాన్ని ఇవ్వాలి. ప్రతీ జంతువుకు మిగిలిన వాటితోపాటు 20 గ్రాముల ప్రోటీన్లు, 6 గ్రాముల క్రొవ్వు ఇవ్వాలి. ఆ ప్రయోగశాల పరిశీలకులు A, B అనే రెండు రకాల ఆహార మిశ్రమాలను కొన్నారు. మిశ్రమం Aలో 10% ప్రోటీన్లు మరియు 6% క్రొవ్వువున్నాయి. మిశ్రమం Bలో 20% ప్రోటీన్లు, 2% క్రొవ్వు ఉన్నాయి. అయిన వారు ప్రతీ మిశ్రమానికి ఎన్ని గ్రాములు ఉపయోగించాలి ?
సాధన.
జంతువులకు ఇవ్వవలసిన ఆహారంలో 20 గ్రాముల ప్రోటీన్లు ఉండుట కొరకు A మిశ్రమాన్ని x గ్రాములు, Bమిశ్రమాన్ని 5 గ్రాములు ఉపయోగించాలి అనుకుందాం.
లెక్క ప్రకారం ఆహారంలోని ప్రోటీన్లు = 20 గ్రా.
అనగా A మిశ్రమంలోని ప్రోటీన్లు + B మిశ్రమంలోని ప్రోటీన్లు = 20 గ్రా.
\(x \times \frac{10}{100}+y \times \frac{20}{100}\) = 20

\(\frac{x}{10}+\frac{y}{5}\) = 20
⇒ x + 2y = 200 ……… (1)
ఆహారంలోని కొవ్వు = 6 గ్రాములు.
అనగా A మిశ్రమంలోని కొవ్వు + B మిశ్రమంలోని కొవ్వు = 6 గ్రాములు

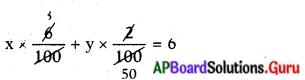
3x + y = 300 ………. (2)
(2) ⇒ y = 30 – 3x ను (1) లో ప్రతిక్షేపించగా.
x + 2 (300 – 3x) = 200
x + 600 – 6x = 200
5x = 200 – 600 = – 400 .
5x = 400
⇒ x = \(\frac{400}{5}\) = 80
⇒ x = 80
x = 80 ని (2) లో రాయగా,
3 (80) + y = 300
⇒ 240 + y = 300
⇒ y = 300 – 240 = 60
∴ సాధన x = 80, y = 60..
∴ A మిశ్రమాన్ని 80 గ్రాములు, B మిశ్రమాన్ని 60 గ్రాములు ఉపయోగించాలి.

సరిచూసుకోవడం :
A మిశ్రమం 80 గ్రా. గల ప్రోటీన్లు (10%) = 80 × \(\frac{10}{100}\) = 8 గ్రా.

A మిశ్రమం 60 గ్రా. గల ప్రోటీన్లు (20%) = 60 × \(\frac{20}{100}\) = 12 గ్రా
మొత్తం ప్రోటీన్లు = 20 గ్రా.