SCERT AP 10th Class Maths Textbook Solutions Chapter 5 వర్గ సమీకరణాలు Exercise 5.1 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 5th Lesson వర్గ సమీకరణాలు Exercise 5.1
ప్రశ్న 1.
క్రింది సమీకరణాలు వర్గ సమీకరణాలు అవునో, కాదో నిర్ణయించండి.
(i) (x + 1)2 = 2(x – 3)
సాధన.
(x + 1)2 = 2(x – 3),
[: (a + b)2 = a2 + 2ab + b2]
⇒ x2 + 2x + 1 = 2x – 6
⇒ x2 + 2x + 1 – 2x + 6 = 0
⇒ x2 + 7 = 0
⇒ x2 + 0. x + 7 = 0
ఇది ax2 + bx + c = 0, b= 0, రూపంలో కలదు. కావున ఇది వర్గ సమీకరణము.
![]()
(ii) x2 – 2x = – 2(3 – x)
సాధన.
x2 – 2x = (- 2) (3 – x)
⇒ x2 – 2x = – 6 + 2x
⇒ x2 – 2x + 6 – 2x = 0.
⇒ x2 – 4x + 6 = 0
ఇది ax2 + bx + c = 0 రూపంలో కలదు. కావున ఇది వర్గ సమీకరణము.
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
సాధన.
(x – 2) (x + 1) = (x – 1)(x + 3)
⇒ x2 + x – 2x – 2 = x2 + 3x – x – 3
⇒ x2 – x – 2 = x2 + 2x – 3
⇒ x2 – x – 2 – x2 – 2x + 3
⇒ – 3x + 1 = 0
దీని పరిమాణం 1. ఇది ax2 + bx + c = 0 రూపంలో లేదు. కావున ఇది వర్గ సమీకరణం కాదు.
(iv) (x – 3) (2x + 1) = x (x + 5)
సాధన.
(x – 3) (2x + 1) = x (x + 5)
⇒ 2x2 + x – 6x – 3 = x2 + 5x
⇒ 2x2 – 5x – 3 – x2 – 5x = 0
⇒ x2 – 10x – 3 = 0
ఇది ax2 + bx + c = 0 రూపంలో కలదు. కావున ఇది వర్గ సమీకరణము.
![]()
(v) (2x – 1)(x – 3) = (x + 5) (x – 1)
సాధన.
(2x – 1) (x – 3) = (x + 5) (x – 1)
⇒ 2x2 – 6x – x + 3 = x2 – x + 5x – 5
⇒ 2x2 – 7x + 3 = x2 + 4x – 5
⇒ 2x2 – 7x + 3 – x2 – 4x + 5 = 0
⇒ x2 – 11x + 8 = 0
ఇది ax2 + bx + c = 0 రూపంలో కలదు. కావున ఇది వర్గ సమీకరణము.
(vi) x2 + 3x + 1 = (x – 2)2
సాధన.
x2 + 3x + 1 = (x – 2)2
[:: (a – b)2 = a2 – 2ab + b2]
⇒ x2 + 3x + 1 = x2 – 4x + 4
⇒ x2 + 3x + 1 – x2 + 4x – 4 = 0
⇒ 7x – 3 = 0
దీని పరిమాణం 1. ఇది ax2 + bx + c = 0 రూపంలో లేదు. కావున ఇది వర్గ సమీకరణం కాదు.
(vii) (x + 2)3 = 2x (x2 – 1)
సాధన.
(x + 2)3 = 2x (x2 – 1)
[∵ (a + b)3 = a3 + 3a2b + 3ab2 + b3)]
⇒ x3 + 6x2 + 12x + 8 = 2x3 – 2x
⇒ x3 + 6x2 + 12x + 8 – 2x3 + 2x = 0
⇒ – x3 + 6x2 + 14x + 8 = 0
దీని పరిమాణం 3. ఇది ax2 + bx + c = 0 రూపంలో లేదు. కావున ఇది వర్గ సమీకరణం కాదు.
![]()
(viii) x3 – 4x2 – x + 1 = (x – 2)3
సాధన.
x3 – 4x2 – x + 1 = (x – 2)3
[∵ (a + b)3 = a3 + 3a2b + 3ab2 + b3]
⇒ x3 – 4x2 – x + 1 = x3 – 6×2 + 12x – 8
⇒ x3 – 4x2 – x + 1 – x3 + 6x2 – 12x + 8
⇒ 2x2 – 13x + 9 = 0
ఇది ax2 + bx + c = 0 రూపంలో కలదు. కావున ఇది వర్గ సమీకరణము.
ప్రశ్న 2.
క్రింది వానికి సరియగు వర్గ సమీకరణాలను కనుగొనుము.
i) ఒక దీర్ఘచతురస్రాకార స్థలము యొక్క వైశాల్యము 528 చ.మీ. దీని పొడవు, వెడల్పు యొక్క రెట్టింపు కంటే ఒక మీటరు ఎక్కువ. అయిన దాని పొడవు, వెడల్పులను కనుగొనుటకు అవసరమైన వర్గ సమీకరణమును కనుగొనుము.
సాధన.
దీర్ఘచతురస్ర వెడల్పు x మీ. అనుకొనిన
‘పొడవు = 2x + 1.
లెక్క ప్రకారం దీర్ఘ చతురస్ర వైశాల్యం = 528 చ.మీ.
పొడవు × వెడల్పు = 528.
(2x + 1) (x) = 528
2x2 + x = 528
2x2 + x – 528 = 0
∴ పై వర్గ సమీకరణం యొక్క మూలాలలో సాధ్యమైన విలువ దీర్ఘచతురస్రం యొక్క వెడల్పు అవుతుంది. వెడల్పు సహాయంతో పొడవును కనుగొనవచ్చును.
![]()
(ii) రెండు వరుస ధన పూర్ణ సంఖ్యల లబ్దము 306. అయిన ఆ సంఖ్యలను కనుగొనుటకు అవసరమయ్యే వర్గ సమీకరణమును కనుగొనుము/రాయుము.
సాధన.
రెండు వరుస ధన పూర్ణసంఖ్యలు x, x + 1 అనుకొందాం.
లెక్క ప్రకారం రెండు వరుస ధనసంఖ్యల లబ్దం = 306
x(x + 1) = 306
x2 + x = 306
∴ x2 + x – 306 = 0
పై వర్గ సమీకరణం యొక్క మూలాలలోని ధన విలువ చిన్న సంఖ్య అవుతుంది. దాని నుండి రెండవ సంఖ్యను కనుగొనవచ్చును..
(iii) రోహన్ తల్లి, రోహన్ కంటే 26 సం||లు పెద్దది. 3సం||లు తరువాత వారిద్దరి వయస్సుల లబ్దం 360. అయిన రోహన్ యొక్క ప్రస్తుత వయస్సును కనుగొనుటకు అవసరమయ్యే వర్గసమీకరణమును రాయుము.
సాధన.
రోహన్ ప్రస్తుత వయస్సు = x సం||లు అనుకొంటే
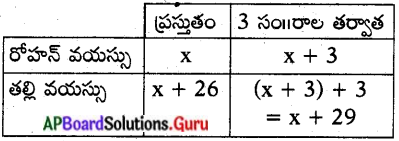
లెక్క ప్రకారం 3 సం||ల తర్వాత వారిద్దరి వయస్సుల లబ్దం = 360
(x + 3) (x + 29) = 360
= x 2+ 29x + 3x + 87 = 360
= x2 + 32x + 87-360 = 0
= x2 + 32x – 273 = 0
పై వర్గ సమీకరణం యొక్క మూలాలలోని ధన విలువ రోహన్ యొక్క వయస్సు అవుతుంది.
![]()
(iv) 480 కి.మీ. దూరమును ఒక రైలు ఏకరీతి వేగముతో ప్రయాణిస్తుంది. ఒకవేళ ఇదే రైలు ఇప్పటి వేగం కంటే 8కి.మీ తక్కువ వేగముతో ప్రయాణిస్తే గమ్యం చేరుటకు పట్టే కాలం 3 గం||లు పెరుగుతుంది. అయిన రైలు వేగమును కనుగొనుటకు కావలసిన వర్గ సమీకరణమును కనుగొనుము.
సాధన.
రైలు వేగం = x కి.మీ. | గం|| అనుకొంటే
480 కి.మీ. ప్రయాణించుటకు పట్టే కాలం = \(\frac{480}{x}\) గం||.
రైలు వేగం 8 కి.మీ. | గం|| తగ్గిన తర్వాత రైలు వేగం = (x – 8) కి.మీ. గం||.
రైలు 480 కి.మీ. ప్రయాణించుటకు పట్టే కాలం = \(\frac{480}{x-8}\) గం॥..
లెక్క ప్రకారం \(\frac{480}{x-8}=\frac{480}{x}+3\)
∴ \(\frac{480}{x-8}=\frac{480}{x}\) = 3
\(\left[\frac{x(480)-(x-8)(480)}{x(x-8)}\right]\)
⇒ 3840 = 3(x2 – 8x)
⇒ 3x2 – 24x = 3840
⇒ 3x2 – 24x – 3840 = 0
⇒ 3(x2 – 8x – 1280) = 0
⇒ x2 – 8x – 1280 = 0.
పై వర్గ సమీకరణం యొక్క మూలాలలో ఒకటి రైలు యొక్క వేగము అవుతుంది.