AP Board 10th Class Maths Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 4 రెండు చరరాశులలో రేఖీయ సమీకరణాల జత InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 4th Lesson రెండు చరరాశులలో రేఖీయ సమీకరణాల జత InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
కింది సమీకరణాల వ్యవస్థను సాధించండి. (పేజీ నెం. 79)
(i) x – 2y = 0; 3x + 4y = 20
(ii) x + y = 2; 2x + 2y = 4
(iii) 2x – y = 4; 4x – 2y = 6
సాధన.
(i) x – 2y = 0; 3x + 4y = 20
x – 2y = 0
– 2y = – x
2y = x
y = \(\frac{x}{2}\)

3x + 4y = 20
4y = 20 – 3x
y = \(\frac{20-3 x}{4}\)

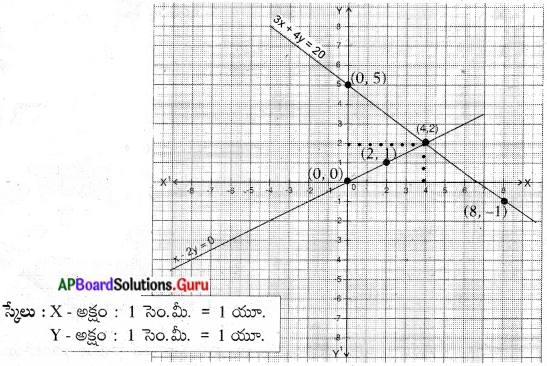
∴ సాధన ఇచ్చిన సమీకరణాల సాధన జత ఖండనరేఖలు.
(x, y) = (4, 2)
x = 4, y = 2.

(ii) x + y = 2;
2x + 2y = 4
సాధన.
x + y = 2
y = 2 – x

2x + 2y = 4
2y = 4 – 2x
⇒ y = \(\frac{4-2 x}{2}\)

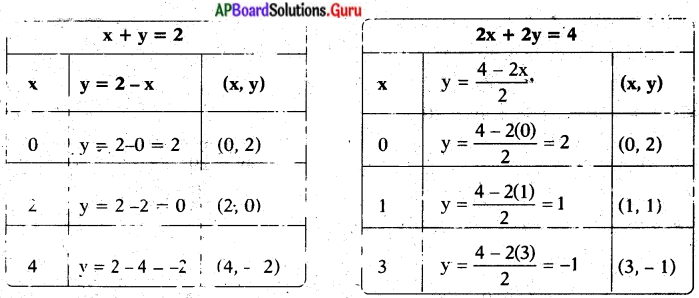
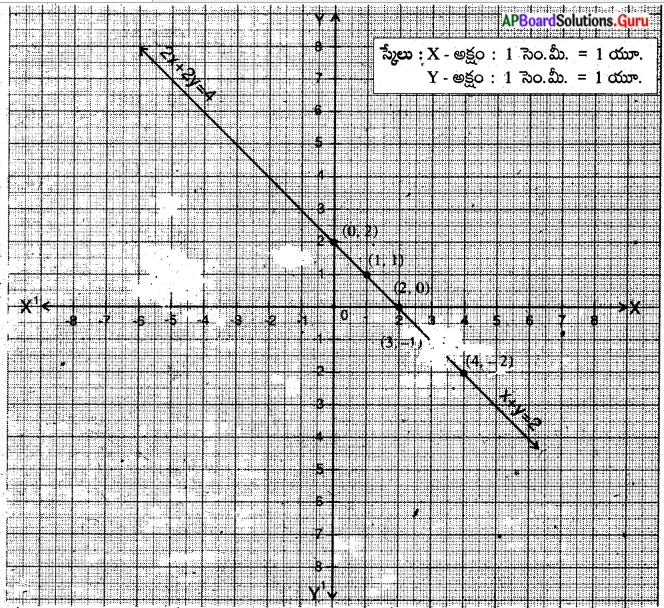
ఇచ్చిన సమీకరణాల జత ఏకీభవించే రేఖలు. కావున అనంత సాధనలు ఉంటాయి.

(iii) 2x – y = 4
4x – 2y = 6
సాధన.
2x – y = 4
– y = 4 – 2x
y = 2x – 4

4x – 2y = 6
– 2y = 6 – 4x
⇒ 2y = 4x – 6
⇒ y = \(\frac{4 x-6}{2}\)

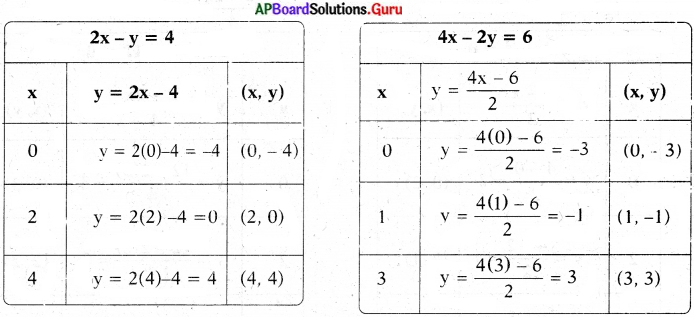
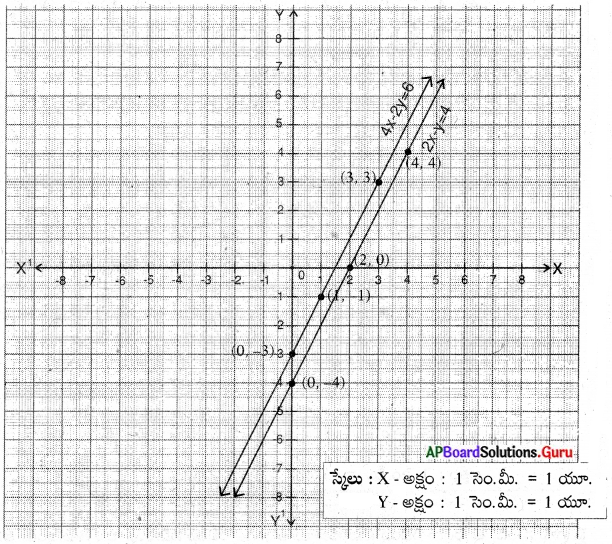
∴ ఇచ్చిన సమీకరణాల జత అసంగత రేఖీయ సమీకరణాలు. కావున సాధన ఉండదు.

ప్రశ్న 2.
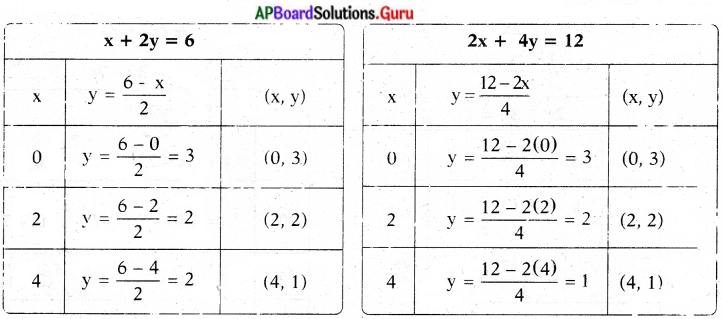
x + 2y – 4 = 0 మరియు 2x + 4y – 12 = 0 సమీకరణాలను గ్రాఫ్ ద్వారా సూచించండి. వ్యాఖ్యానించండి. (పేజీ నెం. 79)
సాధన.
x + 2y – 4 = 0 ……………….(1)
2x + 4y – 12 = 0 …………….. (2)
x + 2y – 4 = 0
2x + 4y – 12 = 0
2y = 4 – x
y = \(\frac{4-x}{2}\)

2x + 4y – 12 = 0
4y = 12 – 2x
y = \(\frac{12-2 x}{4}\)

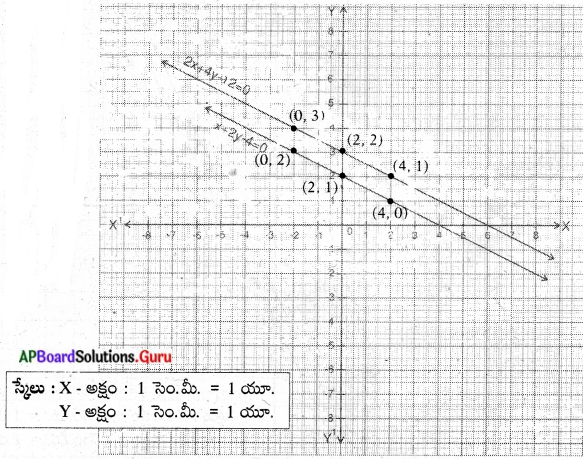
పై గ్రాఫ్ నుండి, ఈ రెండు రేఖీయ సమీకరణాలు అసంగత రేఖీయ సమీకరణాలని తెలుస్తుంది. అనగా సమాంతరాలు, ఖండన బిందువులు లేవు, ఉమ్మడి సాధన లేదు.

ప్రశ్న 3.
కింది సమీకరణాల జతలకు ఏకైక సాధన, అనంత సాధనలా లేక సాధనలు లేవో సరిచూడండి. వాటిని గ్రాఫ్ పద్ధతి ద్వారా సాధించండి.
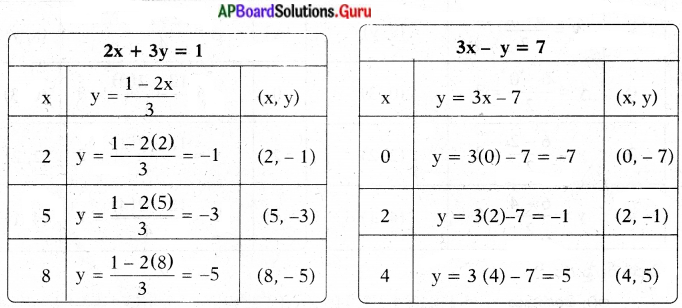
(i) 2x + 3y = 1
3x – y = 7

(ii) x + 2y = 6
2x + 4y = 12

(iii) 3x + 2y = 6
6x + 4y = 18 (పేజీ నెం. 83)
సాధన.
(i) 2x + 3y = 1, 3x – y = 7
2x + 3y = 1 ⇒ 2x + 3y – 1 = 0 ………. (1)
3x – y = 7 ⇒ 3x – y – 7 = 0 ………. (2)
a₁ = 2, b₁ = 3, c₁ = – 1
a₂ = 3, b₂ = – 1, c₂ = – 7
\(\frac{a_{1}}{a_{2}}=\frac{2}{3}\),

\(\frac{b_{1}}{b_{2}}=\frac{3}{-1}\) = – 3

\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}\) కావున ఇచ్చిన రేఖీయ సమీకరణాల జత ఏకైక సాధనను కలిగి ఉంటుంది. వీటి రేఖాచిత్రము ఖండన రేఖలు అవుతాయి. 2x + 3y = 1

2x + 3y = 1
3y = 1 – 2x
y = \(\frac{1-2 x}{3}\)

3x – y = 7
– y = 7 – 3x
y = 3x – 7

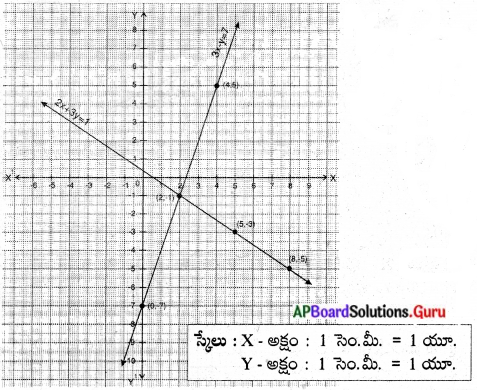
(ii) x + 2y = 6
* 2x + 4y = 12
సాధన.
x + 2y – 6 = 0 … ……. (1)
a₁ = 1, b₁ = 2, c₁ = – 6
2x + 4y – 12 = 0 ………. (2)
a₂ = 2, b₂ = 4, c₂ = – 12

\(\frac{a_{1}}{a_{2}}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{6}{12}=\frac{1}{2}\)

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\)
కావున ఇచ్చిన రేఖీయ సమీకరణాల జత పరస్పరాధారిత రేఖల జత అవుతుంది. వీటికి అనంత సాధనలు సమకరణాల జత పర సాధనలు ఉంటాయి, మరియు వీటి గ్రాఫ్ ఏకీభవించే రేఖలు.
x + 2y = 6
2y = 6 – x
y = \(\frac{6-x}{2}\)

2x + 4y = 12
4y = 12 – 2x
y = \(\frac{12-2 x}{4}\)

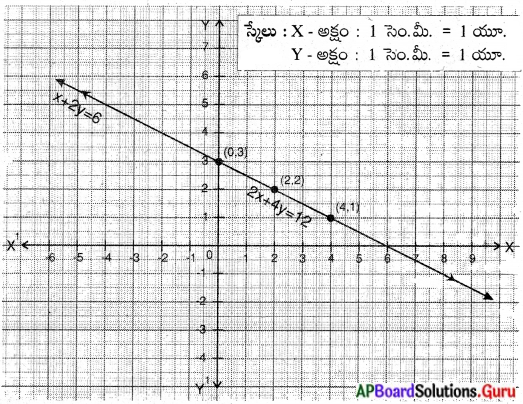
సాధన రేఖపై గల అన్ని బిందువులు సాధనలు అవుతాయి.

(iii) 3x + 2y = 6
6x + 4y = 18
సాధన.
3x+2y – 6 = 0
⇒ a₁ = 3, b₁ = 2, c₁ = 6

6x+4y – 18 = 0
⇒ a₂ = 6, b₂ = 4, c₂ = 18

\(\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{6}{18}=\frac{1}{3}\)

\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\).
కావున ఇచ్చిన రేఖీయ సమీకరణాలు అసంగత సమీకరణాలు అవుతాయి. కావున వీటికి a b2 C2 సాధన ఉండదు. వీటి రేఖాచిత్రం సమాంతర రేఖలు
3x + 2y = 6
2y = 6 – 3x
y = \(\frac{6-3 x}{2}\)

6x + 4y = 18
4y = 18 – 6x
y = \(\frac{18-6 x}{4}\)

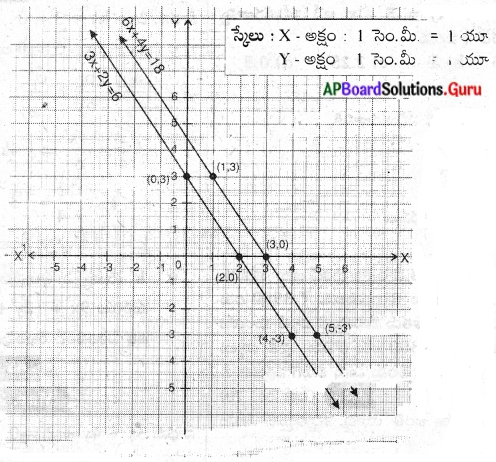
ప్రయత్నించండి:
ఈ కింది ప్రశ్నలకు సరియైన సమాధానాన్ని గుర్తించండి. (పేజీ నెం. 75, 76)

ప్రశ్న 1.
ఈ కింది సమీకరణాలలో ఏది రేఖీయ సమీకరణం కాదు ?
a) 5 + 4x = y + 3
b) x + 2y = y – x
c) 3 – x = y² + 4
d) x + y = 0
సాధన.
c) 3 – x = y² + 4

ప్రశ్న 2.
ఈ క్రింది వాటిలో ఏది ఏక చరరాశిలో రేఖీయ సమీకరణము ?
a) 2x + 1 = y – 3
b) 2t – 1 = 2t + 5
c) 2x – 1 = x²
d) x² – x + 1 = 0
సాధన.
b) 2t – 1 = 2t + 5

ప్రశ్న 3.
క్రింది సంఖ్యలలో ఏది 2(x + 3) = 18 అనే సమీకరణానికి సాధన ?
a) 5
b) 6
c) 13
d) 21
సాధన.
b) 6

ప్రశ్న 4.
2x – (4 – x) = 5 – x అనే సమీకరణాన్ని తృప్తిపరచే x విలువ
a) 4.5
b) 3
c) 2.25
d) 0.5
సాధన.
c) 2.25

ప్రశ్న 5.
x – 4y = 5 అనే సమీకరణానికి
a) సాధనలేదు
b) ఒకే ఒక సాధన
c) రెండు సాధనలు
d) అనంతమైన సాధనలు
సాధన.
d) అనంతమైన సాధనలు

ప్రశ్న 6.
ఎమ్.కె. నగర్ ఉన్నత పాఠశాల క్రికెట్ జట్టు శిక్షకుడు 3 బ్యా ట్లు మరియు 6 బంతులను ₹ 3900 లకు కొనెను. తరువాత అతడు మరియొక బ్యాట్ మరియు 2 బంతులను ₹ 1300 లకు కొనెను. ప్రతీ బ్యాటు మరియు ప్రతీ బంతి వెలను మీరు కనుగొనగలరా ? (పేజీ నెం. 79)
సాధన.
బ్యాటు మరియు బంతి యొక్క కచ్చితమైన వెలను కనుగొనలేము.

ప్రశ్న 7.
కింది సమీకరణాల జతకు ‘p’ యొక్క ఏ విలువకు ఏకైక సాధన ఉంటుందో కనుగొనండి. 2x + py = – 5 మరియు 3x + 3y = – 6 (పేజీ నెం. 83)
సాధన.
2x + py = – 5
⇒ 2x + py + 5 = 0

3x + 3y = – 6
⇒ 3x + 3y + 6 = 0

రేఖీయ సమీకరణాలకు ఏకైక సాధన ఉంటే \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}} \neq \frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}\) కావాలి.
∴ p యొక్క విలువ 2 తప్ప మిగిలిన అన్ని వాస్తవ సంఖ్యలకు ఇచ్చిన రేఖీయ సమీకరణాల జత ఏకైక సాధనను కలిగి ఉంటుంది.

ప్రశ్న 8.
2x – ky + 3 = 0, 4x + 6y – 5 = 0 సమీకరణాల జతకు, ఓ యొక్క ఏ విలువకు అవి సమాంతర రేఖలవుతాయో కనుగొనండి. (పేజీ నెం. 83)
సాధన.
2x – ky + 3 = 0
4x + 6y – 5 = 0 లు సమాంతర రేఖలు అయితే \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}} \neq \frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)
∴ \(\frac{2}{4}=\frac{-k}{6}\)

⇒ – 4k = 12

∴ k = \(\frac{12}{-4}\) = – 3
k = – 3 కి ఇచ్చిన రేఖలు సమాంతరాలు అవుతాయి.

ప్రశ్న 9.
‘k’ యొక్క ఏ విలువకు, 3x + 4y + 2 = 0 మరియు 9x + 12y + k= 0 రేఖా సమీకరణాల జత ఏకీభవించే రేఖలవుతాయో కనుగొనండి. (పేజీ నెం. 83)
సాధన.
3x + 4y + 2 = 0
9x + 12y + k = 0
రేఖీయ సమీకరణాల జత ఏకీభవించే రేఖలు అయితే \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)

\(\frac{3}{9}=\frac{4}{12}=\frac{2}{k}\) \(\frac{4}{12}=\frac{2}{k}\)

⇒ \(\frac{1}{3}=\frac{2}{k}\)

k = 6.

k = 6 కి ఇచ్చిన రేఖలు ఏకీభవించే రేఖలు అవుతాయి.

ప్రశ్న 10.
‘p’ యొక్క ఏ ధనవిలువలకు కింది సమీకరణాల జతకు అనంత సాధనలుంటాయో కనుగొనండి. px + 3y – (p- 3) = 0 12x + py – p = 0 (పేజీ నెం. 83)
సాధన.
px + 3y – (p – 3) = 0
12x + py – p = 0
సమీకరణాల జతకు అనంత సాధనలుంటే ఇవి పరస్పరాధారిత రేఖల జత అవుతుంది. కావున \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)

∴ \(\frac{p}{12}=\frac{3}{p}=\frac{-(p-3)}{-p}\)

∴ \(\frac{\mathrm{p}}{12}=\frac{3}{\mathrm{p}}\)

⇒ p² = 36
⇒ p = √36 = 6
∴ p = 6

(లేదా)

\(\frac{p}{12}=\frac{-(p-3)}{-p}\)
p² = 12(p – 3)
p² – 12p + 36 = 0
p² = 12p – 36
(p – 6)² = 0
p – 6 = 0
∴ p = 6.

(లేదా)

\(\frac{3}{p}=\frac{-(p-3)}{-p}\)
(p – 3) = 3p
p² – 3p = 3p
p² – 6p = 0
p (p – 6) = 0
p = 0 లేదా p = 6
p ధనవిలువ కావాలి.
∴ p = 6.
p = 6 అయినప్పుడు ఇచ్చిన రేఖలకు అనంత సాధనలు ఉంటాయి.

ఆలోచించి, చర్చించి రాయండి:

ప్రశ్న 1.
ఈ కింద రెండు సందర్భాలు ఇవ్వబడ్డాయి.
(i) 1 కిలో బంగాళదుంపలు మరియు 2 కిలోల టమాటాల. మొత్తము వెల ₹ 30. రెండు రోజుల తరువాత, 2 కిలోల బంగాళదుంపలు మరియు 4 కిలోల టమాటాల మొత్తము వెల ₹ 66.
(ii) ఎమ్.కె.నగర్ ఉన్నత పాఠశాల క్రికెట్ జట్టు శిక్షకుడు 3 బ్యాట్లు మరియు 6 బంతులను ₹ 3,900 లకు కొనెను. తరువాత అతడు మరియొక బ్యాట్ మరియు 2 బంతులను ₹ 1,300 లకు కొనెను.
పై ప్రతీ సందర్భంలో అవ్యక్తరాశులను గుర్తించండి. ప్రతీ సందర్భంలో రెండు చరరాశులు ఉండటాన్ని మనం గమనించవచ్చును. (పేజీ నెం. 173)
సాధన.
అవ్యక్త రాశులు
(i) కిలో బంగాళదుంపల వెల మరియు కిలో టమాటాల వెల. .
(ii) ఒక బ్యాట్ వెల మరియు ఒక బంతి వెల.

ప్రశ్న 2.
పరస్పరాధారిత రేఖీయ సమీకరణాల జత ఎల్లప్పుడూ సంగత జత అవుతుందా ? ఎందుకు అవుతుంది (లేదా) ఎందుకు కాదు ? కారణాన్ని వివరించండి. (పేజీ నెం. 79)
సాధన.
పరస్పరాధారిత రేఖీయ సమీకరణాల జత ఎల్లప్పుడు సంగత జత అవుతుంది.
పరస్పరాధారిత జత సాధనలను కలిగి ఉంటుంది. కావున సంగత జత అవుతుంది.
ఎందుకనగా \(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{\mathrm{b}_{1}}{\mathrm{~b}_{2}}=\frac{\mathrm{c}_{1}}{\mathrm{c}_{2}}\)

ఇవి చేయండి:

ప్రశ్న 1.
క్రింద యిచ్చిన ప్రతీ జత సమీకరణాలను ప్రతిక్షేపణ పద్ధతి ద్వా రా సాధించండి. (పేజీ నెం. 88)

1) 3x – 5y = – 1
x – y = – 1
సాధన.
3x – 5y = – 1 ………… (1)
x-y=-1 ……….. (2)
(2) ⇒ – y = – x – 1
⇒ y = x + 1
y = x + 1 ను (1) లో ప్రతిక్షేపించగా.
3x – 5(x + 1) = – 1
3x – 5x – 5 = – 1
– 2x = – 1 + 5
– 2x = 4
⇒ 2x = – 4
⇒ x = \(\frac{-4}{2}\) = – 2
x = – 2 ని (2) లో ప్రతిక్షేపించగా,
– 2 – y = – 1.
– y = – 1 + 2
⇒ – y = 1
⇒ y = – 1
∴ సాధన x = – 2, y = – 12

సరిచూడటం :
x = – 2, y = – 1 లను (1)లో ప్రతిక్షేపించగా,
3(- 2) – 5 (- 1) = – 1
– 6 + 5 = – 1
-1 = – 1.

ప్రశ్న 2.
x + 2y = – 1
2x – 3y = 12
సాధన.
x + 2y = – 1 ………….(1)
2x – 3y = 12 …………….(2)
(1) ⇒ x = – 1 – 2y ను (2) లో ప్రతిక్షేపించగా,
2 (- 1 – 2y) – 3y = 12
– 2 – 4y – 3y = 12
– 7y = 12 + 2
⇒ – 7y = 14
⇒ 7y = – 14
∴ y = \(\frac{-14}{7}\) = – 2
y = – 2 ను (1) లో ప్రతిక్షేపించగా
x + 2 (- 2) = – 1
x – 4 = – 1
⇒ x = – 1 + 4 = 1
∴ సాధన x = 3, y = – 2.

సరిచూడటం :
x = 3, y = – 2ను (2)లో రాయగా.
2(3) – 3(- 2) = 12
6 + 6 = 12
⇒ 12 = 12 .

ప్రశ్న 3.
2x + 3y = 9; 3x + 4y = 5
సాధన.
2x + 3y = 9 …………….(1)
3x + 4y = 5 …………… (2)
(1) ⇒ 3y = 9 – 2x
y = \(\frac{9-2 x}{3}\) ని (2) లో ప్రతిక్షేపించగా.
3x + 4(\(\frac{9-2 x}{3}\)) = 5

3x + \(\frac{36-8 x}{3}\) = 5

\(\frac{9 x+36-8 x}{3}\) = 5

x + 36 = 15 ⇒ x = 15
x = – 21
x = – 21 ని (1) లో ప్రతిక్షేపించగా,
2(- 21) + 3y = 9
42 + 3y = 9
⇒ 3y = 9 + 42
⇒ 3y = 51
⇒ y = \(\frac{51}{3}\) = 17
సాధన x = – 21, y = 17

సరిచూడటం :
x = – 21, y = 17 లను (2) లో రాయగా
3(- 21) + 4(17) = 5
– 63 + 68 = 5.

ప్రశ్న 4.
x + \(\frac{6}{y}\) = 6;
3x – \(\frac{8}{y}\) = 5
సాధన.
x + \(\frac{6}{y}\) = 6 ………..(1)
3x – \(\frac{8}{y}\) = 1 ………….(2)
(1) ⇒ x = 6 2 ని (2) లో ప్రతిక్షేపించగా,
3(6 – \(\frac{6}{y}\)) – \(\frac{8}{y}\) = 5
18 – \(\frac{18}{y}\) – \(\frac{8}{y}\) = 5
\(\frac{-26}{y}\) = 5 – 18
⇒ \(\frac{-26}{y}\) = – 13
⇒ \(\frac{26}{y}\) = 13
⇒ 13 y = 26
⇒ y = \(\frac{26}{13}\) = 2
y = 2 ను (2) లో ప్రతిక్షేపించగా
3x – \(\frac{8}{2}\) = 5
⇒ 3x – 4 = 5
⇒ 3x = 5 + 4 = 9
⇒ x = 3, y = 2.

(లేదా)

x + \(\frac{6}{y}\) = 6 ………….(1)
3x – \(\frac{8}{y}\) = 5 ………..(2)
(1) ⇒ \(\frac{6}{y}\) = 6 – x
\(\frac{1}{y}=\frac{6-x}{6}\)ని (2) లో రాయగా,
3x – 8(\(\frac{6-x}{6}\)) = 5
3x – (\(\frac{48-8 x}{6}\)) = 5
\(\frac{18 x-48+8 x}{6}\) = 5
26x – 48 = 30
26x = 30 + 48 = 78
x = \(\frac{78}{26}\) = 3
x = 3ను (1) లో రాయగా,
3 + \(\frac{6}{y}\) = 6
⇒ \(\frac{6}{y}\) = 6 – 3 = 3
3y = 6
⇒ y = \(\frac{6}{3}\) = 2
∴ సాధన. x = 3, y = 2

సరిచూడటం :
x = 3, y = 2 ను (2) లో ప్రతిక్షేపించగా,
3(3) – \(\frac{8}{2}\) = 5
⇒ 9 – 4 = 5
5 = 5.

ప్రశ్న 5.
0.2x + 0.3y = 1.3
0.4x + 0.5y = 2.3
సాధన.
0.2x + 0.3y = 1.3 ……………..(1)
0.4x + 0.5 y = 2.3 …………….(2)
(1) × 10 = 2x + 3y = 13
(2) × 10 = 4x + 5y = 23
(3) ⇒ 3y = 13 – 2x
y = \(\frac{13-2 x}{3}\) ని (4) లో ప్రతిక్షేపించగా,
4x + 5 (\(\frac{13-2 x}{3}\)) = 23
4x + \(\frac{65-10 x}{3}\) = 23
\(\frac{12 x+65-10 x}{3}\) = 23
2x + 65 = 69
⇒ 2x = 69 – 65 = 4
⇒ x = \(\frac{4}{2}\) = 2
x = 2 ను (4) లో ప్రతిక్షేపించగా.
4(2) + 5y = 23
⇒ 8 + 5y = 23
⇒ 5y = 15
⇒ y = \(\frac{15}{5}\) = 3
∴ సాధన. x = 2, y = 3.

సరిచూడటం : x = 2, y = 3ను (1) లో రాయం
0.2 (2) + 0.3 (3) = 1.3
0.4 + 0.9 = 1.3
1.3 = 1.3

ప్రశ్న 6.
√2x + √3y = 0;
√3x – √8y = 0
సాధన.
√2x + √3y = 0 ………… (1)
√3x – √8y = 0 ………… (2)
(1) ⇒ √3y = – √2x
y = \(\frac{-\sqrt{2} x}{\sqrt{3}}\) (2) లో ప్రతిక్షేపించగా,
√3x – √8(\(\frac{-\sqrt{2} x}{\sqrt{3}}\)) = 0
√3x – \(\frac{\sqrt{16} x}{\sqrt{3}}\) = 0
√3x – \(\frac{4}{\sqrt{3}}\) = 0 కావున
x = 0 ను (1) లో ప్రతిక్షేపించగా, √2(0) + √3y = 0
√3y = 0 ⇒ y = 0
సాధన. x = 0, y = 0

సూచన :
ax + by + c₁ = 0
ax + by + c₂ = 0,
c₁ = c₂ = 0 అయితే
x = 0, y = 0 సాధన అవుతుంది.

ప్రశ్న 7.
క్రింది ప్రతీజత రేఖీయ సమీకరణాలను చరరాశిని తొలగించే పద్ధతి ద్వారా సాధించండి. (పేజీ నెం. 89)

1. 8x + 5y = 9; 3x + 2y = 4 .
సాధన.
8x + 5y = 9 ……….. (1)
3x + 2y = 4 ……….. (2)

x = – 2 ను (1) లో ప్రతిక్షేపించగా,
8(- 2) + 5y = 9
– 16 + 5y = 9
⇒ 5y = 9 + 16 = 25
⇒ y = \(\frac{25}{5}\) = 5
సాధన x = – 2, y = 5.

సరిచూడటం :
x = – 2, y = 5ను (2)లో ప్రతిక్షేపించగా.
3(- 2) + 2(5) = 4
– 6 + 10 = 4
4 = 4

2. 2x + 3y = 8; 4x + 6y =7
సాధన.
2x + 3y = 8 ⇒ 2x + 3y – 8 = 0
4x + 6y – 7 = 0
\(\frac{a_{1}}{a_{2}}=\frac{2}{4}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{3}{6}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-8}{-7}=\frac{8}{7}\)

\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
కావున ఇచ్చిన రేఖీయ సమీకరణాల జత అసంగత రేఖీయ సమీకరణాలు. కావున సాధన ఉండదు.

ప్రశ్న 3.
3x + 4y = 25; 5x – 6y = – 9
సాధన.
3x + 4y = 25 ………… (1)
5x – 6y = – 9 ………… (2)

x = 3ను (1) లో ప్రతిక్షేపించగా,
3(3) + 4y = 25
9 + 4y = 25
4y = 25 – 9 = 16
y = \(\frac{16}{4}\) = 4
∴ సాధన. x = 3, y = 4.
సరిచూడటం :
x = 3, y = 4ను (2)లో ప్రతిక్షేపించగా,
5(3) – 6(4) = – 9
15 – 24 = – 9
– 9 = – 9

ప్రశ్న 8.
ఒక పోటీ పరీక్షలో, ప్రతీ సరియైన సమాధానానికి 3 మార్కులు వేయగా, ప్రతీ తప్పు సమాధానానికి 1 మార్కు తగ్గించెదరు. ఈ పరీక్షలో మధు 40 మార్కులు సంపాదించెను. ప్రతి సరియైన సమాధానానికి 4 మార్కులు వేసి, ప్రతీ తప్పు సమాధానానికి 2 మార్కులు తగ్గించిన అతనికి 50 మార్కులు వచ్చి ఉండేవి అయిన ఆ పరీక్షలో ఉన్న మొత్తము ప్రశ్నలు ఎన్ని ? (మధు పరీక్ష పత్రములోని అన్ని ప్రశ్నలకు జవాబులు రాసెను) ఈ సమస్యను చరరాశిని తొలగించే పద్ధతిలో సాధించండి. (పేజీ నెం. 91)
సాధన.
ఇచ్చిన సమీకరణములు 3x – y = 40 …………… (1)
4x – 2y = 50 …………….. (2)

∴ x = \(\frac{30}{2}\) = 15
x = 15 ను (1) లో ప్రతిక్షేపించగా,
3(15) – y = 40
45 – y = 40
⇒ – y = 40 – 45 = – 5
⇒ y = 5
∴ సాధన x = 15, y = 5.
పరీక్షలోని మొత్తం ప్రశ్నల సంఖ్య = 15 + 5 = 20

ప్రశ్న 9.
మేరి తన కూతురితో ఇలా చెప్పింది. “7 సంవత్సరముల . క్రితం నా వయస్సు అప్పటి నీ వయస్సుకు 7 రెట్లు. అలాగే యిప్పటి నుండి 3 సంవత్సరముల తరువాత నా వయస్సు నీ వయస్సుకు మూడు రెట్లు ఉంటుంది” అయిన మేరి మరియు ఆమె కూతురి ప్రస్తుత వయస్సును కనుగొనండి. (పేజీ నెం. 92) ఈ సమస్యను ప్రతిక్షేపణ పద్ధతి ద్వారా సాధించండి.
సాధన.
ఇచ్చిన సమీకరణములు
x – 7y + 42 = 0 ………….(1)
x – 3y – 6 = 0 …………(2)
(1) ⇒ x = 7y – 42
⇒ x = 7y – 42 ను (2) లో ప్రతిక్షేపించగా,
7y – 42 – 3y = 6
4y = 6 + 42
⇒ 4y = 48
⇒ y = \(\frac{48}{4}\) = 12
y = 12 ను (1) లో రా యగా,
x – 7 (12) = – 42,
x – 84 = – 42
x = – 42 + 84
⇒ x = 42
సాధన x = 42, y = 12.
మేరి ప్రస్తుత వయస్సు = 42 సంవత్సరాలు
ఆమె కూతురి వయస్సు = 12 సంవత్సరాలు.

ప్రయత్నించండి:

ప్రశ్న 1.
ఇచ్చిన రేఖీయ సమీకరణాలు జతను సాధించండి.
(a – b)x + (a + b)y = a² – 2ab – b
(a + b) (x + y) = a² + b²
సాధన.
(a – b)x + (a + b)y = a² – 2ab – b² …………..(1)
(a + b) (x + y) = a² + b² ………………(2)
⇒ (a + b)x + (a + b)y = a² + b²
(1) – (2);

[(a – b) – (a + b)] x = – 2b (a + b).
(a – b – a – b) x = – 2b (a + b)
– 2b x = – 2b (a + b)
x = \(\frac{-2 b}{-2 b}\) (a + b)
x = a + b
x = a + bని (2) లో ప్రతిక్షేపించగా
(a + b)(a + b) + (a + b) y = a² + b²
a² + 2ab + b² + (a + b) y = a² + b²
(a + b) y = a² + b² – a² – 2ab – b²
(a + b) y = – 2ab
y = \(\frac{-2 a b}{a+b}\)
సాధన.
x = a + b, y = \(\frac{-2 a b}{a+b}\)

సరిచూడటం:
x = a + b, y = \(\frac{-2 a b}{a+b}\)ని (1)లో ప్రతిక్షేపించగా.
(a – b)(a + b) + (a + b)\(\frac{-2 a b}{a+b}\) = a² – 2ab – b²
a² – b² – 2ab = a² – 2ab – b²
a² – 2ab – b² = a² – 2ab – b².

ఉదాహరణలు.

ప్రశ్న 1.
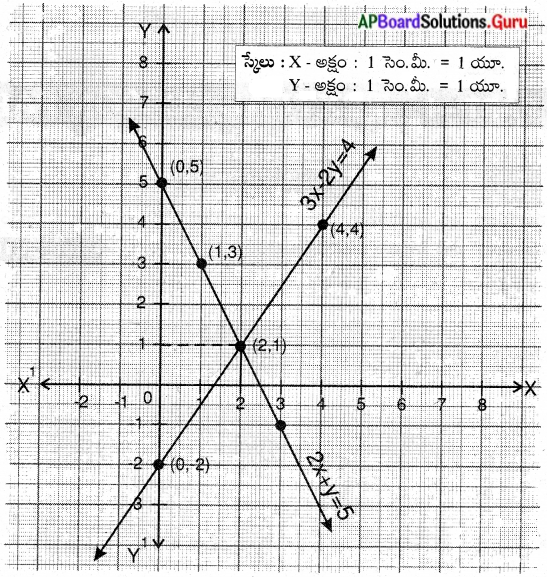
కింది సమీకరణాల జత ఖండనరేఖలా, సమాంతర రేఖలా లేదా ఏకీభవించే రేఖలా సరిచూడండి. ఆ సమీకరణాలు సంగతము అయిన వాటి సాధనను కనుగొనుము.
2x + y -5 = 0, 3x – 2y – 4 = 0 (పేజీ నెం. 80)
సాధన.
2x + y -5 = 0 ……….. (1)
3x – 2y – 4 = 0 ………..(2),
a₁ = 2, b₁ = 1, c₁ = – 5
a₂ = 3, b₂ = – 2, c₂ = – 4
\(\frac{a_{1}}{a_{2}}=\frac{2}{3}\);

\(\frac{b_{1}}{b_{2}}=\frac{1}{-2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-5}{-4}\)

\(\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}\) కావున అవి ఖండన రేఖలు. అనగా సంగత రేఖీయ సమీకరణాల జత.

2x + y – 5 = 0
y = 5 – 2x

3x – 2y -4 = 0
– 2y = 4 – 3x
⇒ 2y = 3x – 4
y = \(\frac{3 x-4}{2}\)

ఇచ్చిన రేఖలు ఖండన రేఖలు సాధన (x, y) = (2, 1)
x = 2, y = 1

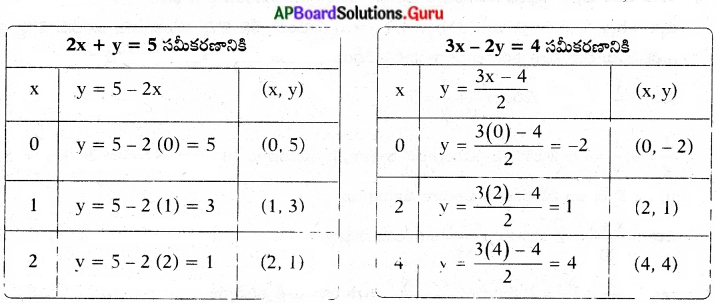
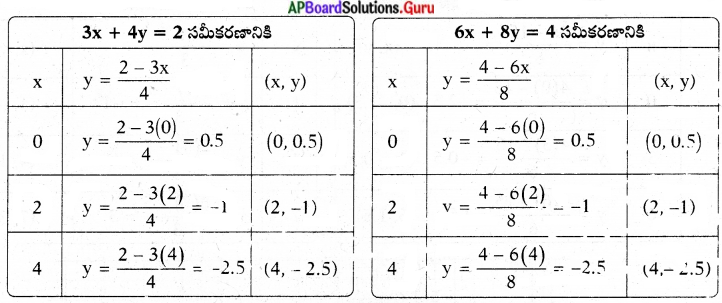
ప్రశ్న 2.
కింది సమీకరణాల జత సంగత జత అవునో, కాదో సరిచూడండి.
3x + 4y = 2 మరియు 6x + 3y = 4 గ్రాఫ్ గీయడం ద్వారా మీ జవాబును సరిచూడండి. (పేజీ నెం. 81)
సాధన.
3x + 4y = 2 మరియు 6x + 8y = 4
3x + 4y = 2 ⇒ 3x + 4y – 2 = 0 …………… (1)
6x + 8y = 4 ⇒ 6x + 8y – 4 = 0 ……………(2)
⇒ a₁ = 3, b₁ = 4, c₁ = – 2;
a₂ = 6, b₂ = 8, c₂ = – 4

\(\frac{a_{1}}{a_{2}}=\frac{3}{6}=\frac{1}{2}\);

\(\frac{b_{1}}{b_{2}}=\frac{4}{8}=\frac{1}{2}\);

\(\frac{c_{1}}{c_{2}}=\frac{-2}{-4}=\frac{1}{2}\)

\(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}\) కావున అవి ఏకీభవించే రేఖలు. కావున ఇచ్చిన రేఖీయ సమీకరణాల జత సంగతం అవుతూ పరస్పరాధారిత సమీకరణాల జత అవుతుంది.

3x + 4y = 2
⇒ 4y = 2 – 3x
⇒ y = \(\frac{2-3 x}{4}\)

6x + 8y – 4
⇒ 8y = 4 – 6x
⇒ y = \(\frac{4-6 x}{8}\)

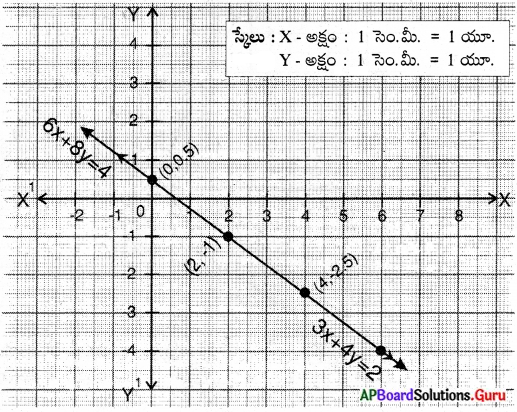
∴ ఇచ్చిన రేఖలు ఏకీభవిస్తున్నాయి.

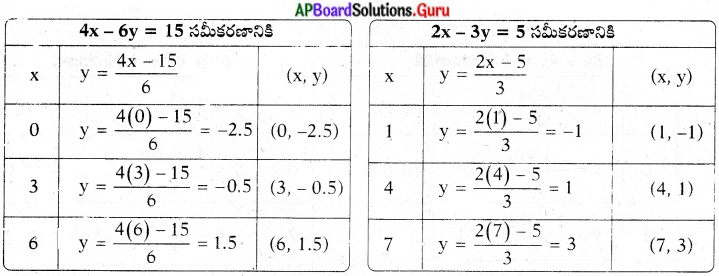
ప్రశ్న 3.
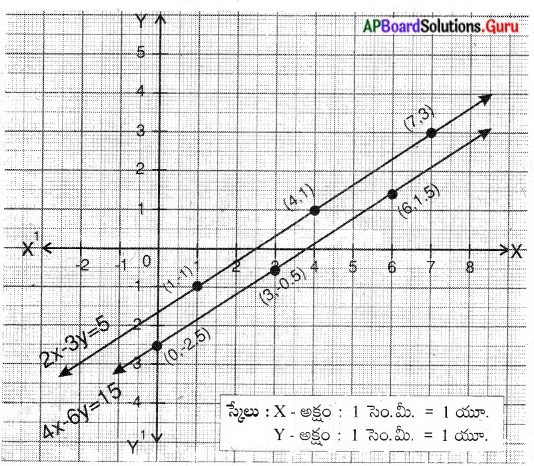
4x – 6y = 15 మరియు 2x – 3y = 5 సమీకరణాలు సంగత సమీకరణాలేమో సరిచూడండి. ఇంకా వాటికి గ్రాఫ్ గీయండి. (పేజీ నెం. 82)
సాధన.
4x – 6y = 15
⇒ 4x – 6y – 15 = 0 …………….(1)
2x – 3y = 5
⇒ 2x – 3y – 5 = 0 …………… (2)
\(\frac{\mathrm{a}_{1}}{\mathrm{a}_{2}}=\frac{4}{2}\) = 2;

\(\frac{b_{1}}{b_{2}}=\frac{-6}{-3}\) = 2;

\(\frac{c_{1}}{c_{2}}=\frac{-15}{-5}\) = 3

∴ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}\)
కావున ఇది అసంగత సమీకరణాలు. వీటికి సాధన లేదు మరియు వీటి రేఖాచిత్రము (గ్రాఫ్) సమాంతర రేఖలు.
4x – 6y = 15
6y = 15 – 4x
6y = 4x – 15
y = \(\frac{4 x-15}{6}\)

2x – 3y = 5
-3y = 5 – 2x
3y = 2x – 5
y = \(\frac{2 x-5}{3}\)

ప్రశ్న 4.
ఒక తోటలో కొన్ని తుమ్మెదలు మరియు పువ్వులు కలవు. ప్రతీ పువ్వుపై ఒక తుమ్మెద వాలినపుడు ఒక తుమ్మెద ,  మిగిలిపోతుంది. ప్రతీ పువ్వుపై రెండు తుమ్మెదలు వాలితే ఒక పువ్వు మిగిలిపోతుంది. అయిన పువ్వులెన్ని ? తుమ్మెదలెన్ని? (పేజీ నెం. 83)
సాధన.
తుమ్మెదల సంఖ్య = x,
పువ్వుల సంఖ్య = y అనుకొనుము.
ప్రతీ పువ్వుపై ఒక తుమ్మెద వాలిన, ఒక తుమ్మెద మిగిలిపోతుంది
∴ x = y + 1
⇒ x – y – 1 = 0 …………….(1)
ప్రతీ పువ్వుపై రెండు తుమ్మెదలు వాలితే, ఒక పువ్వు మిగిలిపోతుంది,
కావున x = 2(y – 1)
⇒ x = 2y – 2
⇒ x – 2y + 2 = 0 …………..(2)
x – y – 1 = 0
– y = 1 – x
y = x – 1

x – 2y + 2 = 0
– 2y = – x – 2
2y = x + 2
y = \(\frac{x+2}{2}\)

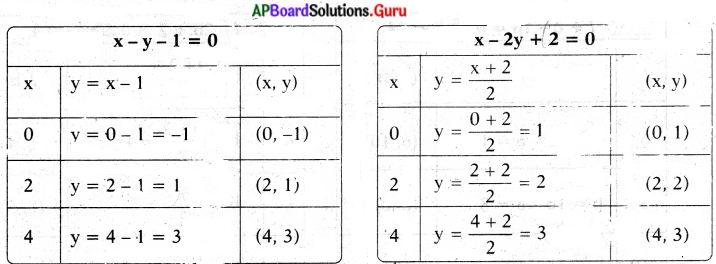
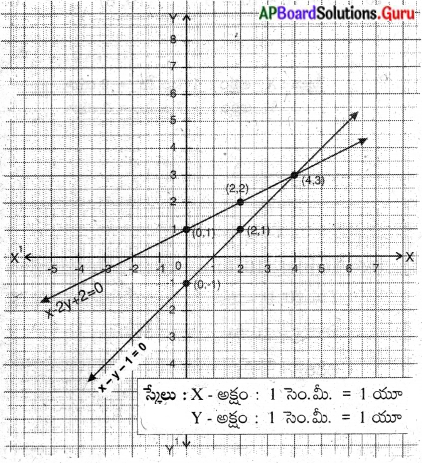
సాధన (x, y) = (4, 3)
x = 4, y = 3
తుమ్మెదల సంఖ్య – 4
పువ్వుల సంఖ్య – 3

ప్రశ్న 5.
ఒక దీర్ఘ చతురస్రాకార స్థలము చుట్టుకొలత 32 మీ. దాని పొడవును 2 మీ పెంచి, వెడల్పును 1 మీ తగ్గించగా దాని వైశాల్యములో ఏ మార్పూ లేక యథాతథంగా ఉండును. అయిన ఆ స్థలము పొడవు, వెడల్పులను కనుగొనుము. (పేజీ నెం. 84)
సాధన.
దీర్ఘచతురస్రాకార స్థలము పొడవు = 1 మీ.
వెడల్పు = b మీ. అనుకొందాం.
∴ దీర్ఘచతురస్ర వైశాల్యం = l × b = lb చ||మీ.
చుట్టుకొలత = 2 (l + b) = 32
⇒ l + b = 16
∴ l + b – 16 = 0 …………… (1)
పొడవును 2 మీ. పెంచి, వెడల్పును 1 మీ తగ్గించినపుడు , కొత్త పొడవు = 1 + 2 మీ., కొత్త వెడల్పు = b – 1 మీ
కొత్త వైశాల్యం = (l + 2) (b – 1) చ||మీ.
= lb – 1 + 2b – 2
వైశాల్యములో మార్పులేదు కాబట్టి,
lb – 1 + 2b – 2 = lb
⇒ lb – 1 + 2b – 2 – lb = 0
⇒ – l + 2b – 2 = 0
∴ l – 2b + 2 = 0 ………… (2)

l + b – 16 = 0
b = 16 – l

l – 2b + 2 = 0
– 2b = – l – 2
2b = l + 2
b = \(\frac{l+2}{2}\)

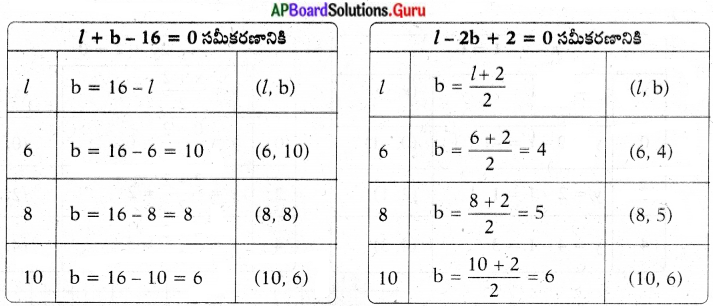
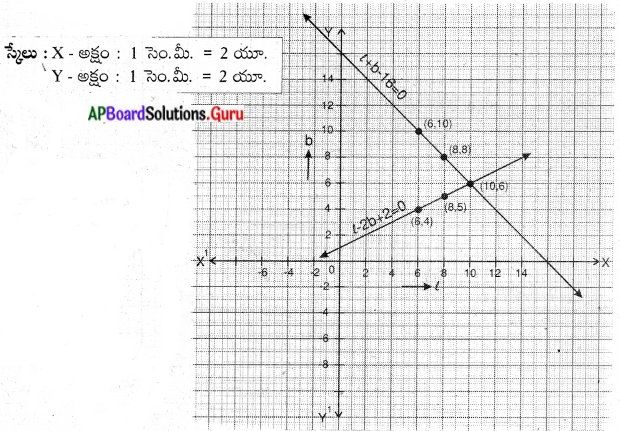
సాధన (l, b) = (10, 6)
l = 10, b = 6
పొడవు = 10 మీ
వెడల్పు = 6 మీ.

ప్రశ్న 6.
ఇచ్చిన సమీకరణాల జతను ప్రతిక్షేపణ పద్ధతి ద్వారా సాధించుము. (పేజీ నెం. 87)
2x – y = 5
3x + 2y = 11
సాధన.
2x – y = 5 ……………..(1)
3x + 2y = 11 ……………. (2)
(1)వ సమీకరణాన్ని ఈ క్రింది విధంగా రాయవచ్చును
y = 2x – 5 (సోపానము 1)
దీనిని (2)వ సమీకరణంలో ప్రతిక్షేపించగా
3x + 2(2x – 5) = 11 (సోపానము 2)
3x + 4x – 10 = 11
7x = 11 + 10 = 21
x = 21/7 = 3. (సోపానము 3)
x = 3ని సమీకరణం (1) లో ప్రతిక్షేపించగా
2(3) – y = 5 (సోపానము 4)
y = 6 – 5 = 1
x, y ల విలువలు (2)లో ప్రతిక్షేపించగా,
3(3) + 2(1) = 9 + 2 = 11
కాబట్టి, కావలసిన సాధన x = 3 మరియు y = 1.
ఇచ్చిన, రెండు సమీకరణాలను x = 3 మరియు y = 1 సంతృప్తి పరుస్తాయి (సోపానము 5)

ప్రశ్న 7.
క్రింద ఇచ్చిన రేఖీయ సమీకరణాల జతను చరరాశిని తొలగించే పద్ధతి ద్వారా సాధించండి. 3x + 2y = 11 . 2x + 3y = 4 (పేజీ నెం. 88)
సాధన.
3x + 2y = 11 ……… (1)
2x + 3y = 4 ……… (2) (సోపానము 1)
ఇచ్చిన సమీకరణాల నుండి చరరాశి ‘y’ని తొలగించాలనుకొనుము. రెండు సమీకరణాలలో ‘y’ గుణకాలు వరుసగా 2 మరియు 3. వాటి క.సా.గు. 6. కావున సమీకరణము (1) ని 3 చే, సమీకరణము (2) ని 2 చే గుణించాలి.

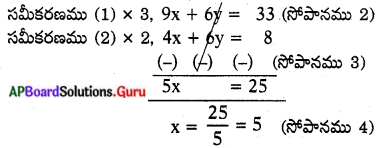
x = 5 విలువను సమీకరణం (1) లో వ్రాయగా,
3(5) + 2y = 11
2y = 11 – 15 = – 4 (సోపానము. 5)
కావున కావలసిన సాధన x = 5, y = – 2.

ప్రశ్న 8.
రుబీనా బ్యాంకు నుండి ₹ 2000 తీసుకొనదలచినది. ఆమె క్యాషియర్‌ను ఆ మొత్తానికి ₹ 50 మరియు ₹ 100 నోట్లు మాత్రమే ఇవ్వమని కోరినది. మొత్తము ఆమెకు 25 నోట్లు వచ్చిన, ఆమెకు ఎన్ని ₹ 50 నోట్లు, ఎన్ని ₹ 100 నోట్లు వచ్చినవో చెప్పగలరా ? (పేజీ నెం. 89)
సాధన.
ఆమెకు వచ్చిన ₹ 50 నోట్ల సంఖ్యను x అని, ₹ 100
నోట్ల సంఖ్యను y అని అనుకొనుము.
అపుడు, x + y = 25 ………. (1) మరియు
50x + 100y = 2000 …….. (2)
వీనిని ప్రతిక్షేపణ పద్ధతిలో సాధించిన;
(1) వ సమీకరణము నుండి x = 25 – y
(2) వ సమీకరణంలో ప్రతిక్షేపించగా,
50 (25 – y) + 100y = 2000
1250 – 50y + 100y = 2000
50y = 2000 – 1250 = 750
y = \(\frac{750}{50}\) = 15
x = 25 – 15 = 10
కావున, రుబీనా పది ₹ 50 నోట్లను, పదిహేను ₹ 100 నోట్లను తీసుకొన్నది.
శ్వేత చరరాశిని తొలగించు పద్ధతి ద్వారా దీనిని సాధించినది.
సమీకరణాలలో, గుణకాలు వరుసగా 1 మరియు 50 కావున,

ఒకే గుర్తు కావున సమీకరణాన్ని తీసివేయగా,

y = \(\frac{-750}{-50}\) = 15

(1)వ సమీకరణంలో y విలువను ప్రతిక్షేపించగా
x + 15 = 25
⇒ x = 25 – 15 = 10
కావున ఆమె పది ₹ 50 నోట్లను, పదిహేను ₹ 100. నోట్లను తీసుకొన్నది.

ప్రశ్న 9.
ఒక పోటీ, పరీక్షలో, ప్రతీ సరియైన సమాధానానికి 3 మార్కులు వేయగా, ప్రతీ తప్పు సమాధానానికి 1 మార్కు తగ్గించెదరు. ఈ పరీక్షలో మధు 40 మార్కులు సంపాదించెను. కాని ప్రతి సరియైన సమాధానానికి 4 మార్కులు వేసి, ప్రతీ తప్పు సమాధానానికి 2 మార్కులు తగ్గించిన అతనికి 50 మార్కులు వచ్చి ఉండేవి అయిన ఆ పరీక్షలో ఉన్న మొత్తము ప్రశ్నలు ఎన్ని ? (మధు పరీక్ష పత్రములోని అన్ని ప్రశ్నలకు జవాబులు రాసెను) (పేజీ నెం. 90)
సాధన.
సరియైన సమాధానముల సంఖ్య x;
తప్పు సమాధానముల సంఖ్య y అనుకొనుము.
ప్రతీ సరియైన సమాధానానికి 3 మార్కులు వేయగా, ప్రతీ తప్పు సమాధానానికి 1 మార్కు తగ్గించెదరు.
అపుడు అతనికి వచ్చిన మార్కులు 40.
3x – y = 40 …………. (1)
ప్రతీ సరియైన సమాధానానికి 4 మార్కులు వేయగా, ప్రతీ తప్పు సమాధానానికి 2 మార్కులు తగ్గించిన అతనికి 50 మార్కులు వచ్చి ఉండేవి.
4x – 2y = 50………… (2)
ప్రతిక్షేపణ పద్దతి :
(1)వ సమీకరణము నుండి, y = 3x – 40
(2)వ సమీకరణములో ప్రతిక్షేపించగా
4x – 2 (3x – 40) = 50
4x – 6x + 80 = 50
– 2x = 50 – 80 = – 30
⇒ x = \(\frac{-30}{-2}\) = 15
x విలువను (1)వ సమీకరణంలో ప్రతిక్షేపించగా
3(15) – y = 40
45 -y = 40
⇒ y = 45 – 40 = 5
కావున పరీక్ష పత్రములోని మొత్తము ప్రశ్నల సంఖ్య = 15 + 5 = 20.

ప్రశ్న 10.
మేరి తన కూతురితో ఇలా చెప్పింది. “7 సంవత్సరముల క్రితం నా వయస్సు అప్పటి నీ వయస్సుకు 7 రెట్లు. అలాగే యిప్పటి నుండి 3 సంవత్సరముల తరువాత నా వయస్సు నీ వయస్సుకు మూడు రెట్లు ఉంటుంది” అయిన మేరి మరియు ఆమె కూతురి ప్రస్తుత వయస్సును కనుగొనండి. (పేజీ నెం. 91)
సాధన.
మేరి ప్రస్తుత వయస్సు x సంవత్సరములు;
ఆమె కూతురి వయస్సు y సంవత్సరములు అనుకొనుము.
7 సంవత్సరముల క్రితం, మేరి వయస్సు (x – 7) సం||. ఆమె కూతురి వయస్సు (y – 7) సం||
x – 7 = 7(y – 7)
x – 7 = 7y – 49
x – 7y + 42 = 0 ……………. (1)
3 సంవత్సరముల తరువాత, మేరి వయస్సు x + 3 మరియు ఆమె కూతురి వయస్సు y + 3
x + 3 = 3(y + 3)
x + 3 = 3y + 9
x – 3y – 6 = 0 ………………..(2)

చరరాశిని తొలగించు పద్ధతి :

x పదానికి ఒకే గుర్తు కావున సమీకరణం (1) నుండి సమీకరణం (2) ను తీసివేయగా

y = \(\frac{-48}{-4}\)
ఈ, y విలువను (2) వ సమీకరణంలో ప్రతిక్షేపించగా
x – 3 (12) – 6 = 0
x = 36 + 6 = 42
కావున మేరి ప్రస్తుత వయస్సు 42 సంవత్సరములు మరియు ఆమె కూతురి వయస్సు 12 సంవత్సరములు.

ప్రశ్న 11.
ఒక ప్రచురణ కర్త, క్రొత్త పాఠ్యపుస్తకాన్ని సిద్ధం చేశాడు. వాటి స్థిర ధర (పునర్విమర్శ, ముద్రణ, టైపింగ్ ఖర్చులు మొదలైనవి) ఒక్కొక్క పుస్తకానికి ₹ 31.25. ఇవి కాక అదనంగా అతడు ఒక పుస్తకము ముద్రణకై ₹ 320000 ఖర్చు చేసెను. ఆ పుస్తకము టోకు ధర పుస్తకానికి ₹ 48.75 (ప్రచురణ కర్తకు వచ్చు సొమ్ము) ఆ ప్రచురణ కర్త ఖర్చులు, రాబడి సమానం కావాలంటే సమతుల్య స్థానం చేరవలెనంటే ఎన్ని పుస్తకాలను అమ్మాలి ? (పేజీ నెం. 92)
వస్తువు ఉత్పాదకతకు అయిన ఖర్చు, వాటి అమ్మకాల ద్వారా వచ్చిన రాబడి సమానంగా ఉండే స్థానాన్ని సమతుల్యతా స్థానము అంటారు.
సాధన.
ప్రచురణ కర్త సమతుల్యతా స్థానం చేరాలంటే ఖర్చులు, రాబడి సమానం కావాలి.
ముద్రణ అయి అమ్మకమయిన పుస్తకాల సంఖ్య x, సమతుల్యతా స్థానము y అనుకొనుము.
అపుడు ఆ ప్రచురణ కర్తకు పుస్తకముద్రణ ఖర్చు, రాబడిల సమీకరణాలు ,
ముద్రణ సమీకరణం y = 320000 + 31.25x ………… (1)
రాబడి సమీకరణం y = 43.75x ……….. (2)
రెండవ సమీకరణము నుండి y విలువను ఒకటవ సమీకరణంలో ప్రతిక్షేపించగా
43.75x = 3,20,000 + 31.25x
12.5x = 3,20,000
x = \(\frac{3,20,000}{12.5}\) = 25,600
25,600 పుస్తకాలను ముద్రించి అమ్మిన అతడు సమతుల్యతా స్థానము చేరును.

ప్రశ్న 12.
క్రింది సమీకరణాల జతను సాధించండి. (పేజీ నెం. 93)
\(\frac{2}{x}+\frac{3}{y}\) = 13
\(\frac{5}{x}-\frac{4}{y}\) = – 2
సాధన.
ఇచ్చిన సమీకరణాల జతను పరిశీలించండి. అవి రేఖీయ సమీకరణాలు కావు. మనకు ఇచ్చిన సమీకరణాలు
2(\(\frac{1}{x}\)) + 3(\(\frac{1}{y}\)) = 13 …………..(1)

5(\(\frac{1}{x}\)) – 4(\(\frac{1}{y}\)) = – 2 …………. (2)
మనం \(\frac{1}{x}\) = p మరియు \(\frac{1}{y}\) = q ప్రతిక్షేపించగా

క్రింది రేఖీయ సమీకరణాల జత ఏర్పడుతుంది
2p + 3q = 13 ………..(3)
5p – 4q = – 2 ……….. (4)
q గుణకాలు 3, 4 మరియు వాటి క.సా.గు 12 చరరాశిని తొలగించే పద్ధతి ద్వారా సమీకరణం

q’ పదములకు వేరువేరు గుర్తులున్నాయి. కావున ఆ సమీకరణాలను కలుపగా
p = \(\frac{46}{23}\) = 2
p విలువను సమీకరణం (3) లో ప్రతిక్షేపించగా
2(2) + 3q = 13
3q = 13 – 4 = 9
కాని, \(\frac{1}{x}\) = p = 2
⇒ x = \(\frac{1}{2}\)
\(\frac{1}{y}\) = q = 3
⇒ y = \(\frac{1}{3}\)

ప్రశ్న 13.
కవిత తన ఇంటిలో మరి రెండు గదులను నిర్మించాలనుకొంది. ఆమె గృహనిర్మాణ కూలీల గురించి ఆరా తీయగా 6 గురు పురుషులు మరియు 8 మంది స్త్రీలు కలిసి ఆ పనిని 14 రోజులలో పూర్తి చేయగలరని తెలిసింది. కాని ఆమెకు తన ఇంటిలోని గదుల నిర్మాణ పని 10 రోజులలోనే పూర్తికావాలి. 8మంది పురుషులు మరియు 12 మంది స్త్రీలు కలిసి ఆ పనిని 10 రోజులలో పూర్తి చేయగలరని తెలుసుకొంది. పురుషుడు లేదా స్త్రీ ఒక్కరే ఆ పనిని పూర్తి చేయాలంటే ఎంత కాలం పడుతుందో ? కనుక్కోండి.(పేజీ నెం. 94)
సాధన.
పురుషుడు ఒక్కడే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలం = x రోజులు అనుకొనుము.
పురుషుడు ఒక్కడే ఒక రోజులో చేయగలిగిన పని = \(\frac{1}{x}\) రోజులు అవుతుంది..
స్త్రీ ఒక్కరే ఆ పనిని పూర్తి చేయుటకు పట్టు కాలం = y రోజులు అనుకొనిన
స్త్రీ ఒక్కరే ఒక రోజులో చేయగలిగిన పని = \(\frac{1}{y}\) అవుతుంది.
8 మంది పురుషులు మరియు 12 మంది స్త్రీలు ఆ పనిని 10 రోజులలో పూర్తి చేయగలరు.
అనగా 8 మంది పురుషులు మరియు 12 మంది స్త్రీలు ఒక రోజులో చేయగలిగిన పని = \(\frac{1}{10}\) ……… (1)
8 మంది పురుషులు ఒక రోజులో చేయగలిగిన పని 8 × \(\frac{1}{x}\) = \(\frac{8}{x}\)
అదే విధంగా 12 మంది స్త్రీలు ఒక రోజులో 12 చేయగలిగిన పని 12 × \(\frac{1}{y}\) = \(\frac{12}{y}\)
8 మంది పురుషులు మరియు 12 మంది స్త్రీలు ఒక రోజులో చేయగలిగిన మొత్తము పని = \(\frac{8}{x}\) + \(\frac{12}{y}\) ……….. (2)
(1), (2) సమీకరణాల నుండి,
\(\left(\frac{8}{x}+\frac{12}{y}\right)=\frac{1}{10}\)

10 \(\left(\frac{8}{x}+\frac{12}{y}\right)\) = 1

⇒ \(\frac{80}{x}+\frac{120}{y}\) = 1 ………. (3)
అలాగే, 6 గురు పురుషులు మరియు 8 మంది స్త్రీలు ఆ పనిని 14 రోజులలో పూర్తి చేయగలరు. 6 గురు పురుషులు మరియు 8 మంది స్త్రీలు ఒక రోజులో చేయగలిగిన పని = \(\frac{6}{x}+\frac{8}{y}=\frac{1}{14}\)

⇒ 14 \(\left(\frac{6}{x}+\frac{8}{y}\right)\) = 1
⇒ \(\left(\frac{84}{x}+\frac{112}{y}\right)\) = 1 …………. (4)
(3), (4) సమీకరణాలను పరిశీలించండి. అవి రేఖీయ సమీకరణాలేనా?
వాటి సాధన మనం ఎలా కనుగొంటాము? \(\frac{1}{x}\) = u మరియు \(\frac{1}{y}\) = 1
ప్రతిక్షేపించడం ద్వారా వాటిని మనం రేఖీయ సమీకరణాలుగా మార్చవచ్చును.
(3) వ సమీకరణాన్ని రేఖీయ సమీకరణంలా మార్చగా
80u + 120v = 1 ……….. (5)
(4) వ సమీకరణాన్ని రేఖీయ సమీకరణంలా మార్చగా
84u + 112v = 1 ……….. (6)
80 మరియు 84 ల క.సా.గు. 1680. చరరాశిని తొలగించు పద్ధతి ద్వారా,
సమీకరణం (3) × 21;
(21 × 80)u + (21 × 120)v = 21
సమీకరణం (4) × 20;
(20 × 84)u + (20 × 112)v = 20

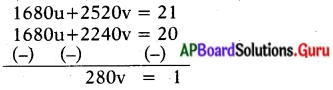
u కు ఒకే గుర్తు కావున తీసివేయగా v = \(\frac{1}{280}\)
సమీకరణం (5) లో ప్రతిక్షేపించగా
80u + 120 x \(\frac{1}{280}\) = 1
80u = 1 – \(\frac{3}{7}\) = \(\frac{7-3}{7}=\frac{4}{7}\)
u = \(\frac{4}{7}\) × \(\frac{1}{80}\)
= \(\frac{1}{140}\)
కావున పురుషుడొక్కడే ఆ పనిని 140 రోజులలో, స్త్రీ ఒక్కరే ఆ పనిని 280 రోజులలో పూర్తి చేయగలరు.

ప్రశ్న 14.
ఒక వ్యక్తి 370 కి.మీ. దూరాన్ని కొంత దూరం రైలులో, కొంతదూరం కారులో ప్రయాణించాడు. అతను 250కి.మీ దూరాన్ని రైలులో, మిగిలిన దూరాన్ని కారులో ప్రయాణించగా అతనికి 4 గంటలు పట్టినది. అదే అతను 130 కి.మీ దూరం రైలులో, మిగిలిన దూరం కారులో ప్రయాణిస్తే అతనికి 18 నిమిషాల కాలం ఎక్కువ పట్టేది. రైలు మరియు కారుల వేగాన్ని కనుగొనండి. (పేజీ నెం. 96)
సాధన.
రైలు వేగం x కి.మీ/గం., కారు వేగం 5 కి.మీ/గం. అనుకొనుము.

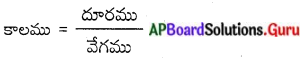
అని మనకు తెలుసు.
1వ సందర్భంలో, రైలు ప్రయాణానికి పట్టిన కాలం = \(\frac{250}{x}\) గం.
కారు ప్రయాణానికి పట్టిన కాలం = \(\frac{140}{y}\) గం.
మొత్తం కాలం = రైలు ప్రయాణానికి పట్టినకాలం + కారు ప్రయాణానికి పట్టిన కాలం = \(\frac{250}{x}\) + \(\frac{140}{y}\)
కాని మొత్తం ప్రయాణానికి పట్టిన కాలం 4 గంటలు కావున
\(\frac{250}{x}\) + \(\frac{140}{y}\) = 4

⇒ \(\frac{125}{x}+\frac{60}{y}\) = 2
మరల 130 కి.మీ దూరం రైలులో మిగిలిన దూరం కారులో ప్రయాణించినపుడు 130 కి.మీ రైలు

ప్రయాణానికి పట్టిన కాలం = \(\frac{130}{x}\) గం.
240 కి.మీ (370 – 130) కారు ప్రయాణానికి పట్టిన కాలం = \(\frac{240}{y}\) గం.
మొత్తం కాలం = \(\frac{130}{x}+\frac{240}{y} \)
కాని ప్రయాణానికి పట్టిన మొత్తం. కాలం 4 గంటల 18 నిమిషాలు 4\(\frac{18}{60}\) = 4\(\frac{3}{10}\) గం.
అనగా, \(\frac{130}{x}+\frac{240}{y}=\frac{43}{10}\) …………..(2)
(1) (2) సమీకరణాలలో \(\frac{1}{x}\) = a మరియు \(\frac{1}{y}\) = b ప్రతిక్షేపించగా
125a + 60b = 2 ……………(3)
130a+ 240b = 7 …………. (4)
60, 240 ల క.సా.గు. 240. చరరాశిని తొలగించే పద్ధతిని ఉపయోగించగా,

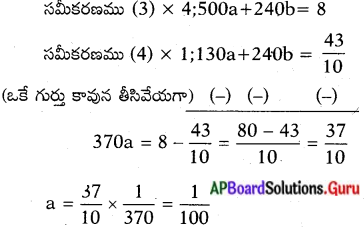
a = \(\frac{1}{100}\) ను సమీకరణం (3) లో ప్రతిక్షేపించగా
(125 × \(\frac{1}{100}\)) + 60b = 2
60b = 2 – \(\frac{5}{4}\)
= \(\frac{8-5}{4}=\frac{3}{4}\)

b = \(\frac{3}{4}\) × \(\frac{1}{60}\) = \(\frac{1}{80}\)
కావున a = \(\frac{1}{100}\) మరియు b = \(\frac{1}{80}\)
\(\frac{1}{x}=\frac{1}{100}\) మరియు \(\frac{1}{y}=\frac{1}{80}\)
x = 100 కి.మీ/గం. మరియు y = 80 కి.మీ/గం కావున రైలు వేగం 100 కి.మీ/గం. మరియు కారు వేగం 80 కి.మీ/గం.