AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు Exercise 6.3

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు Exercise 6.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు Exercise 6.3

ప్రశ్న 1.
క్రింది అంకశ్రేఢులలో పేర్కొన్న పదాల మొత్తాలను ‘ కనుగొనుము.
(i) 2, 1, 12, ……… 10 పదాలు.
సాధన.
ఇచ్చిన A.P : 2, 7, 12, …….. 10 పదాలు.
a = 2; d = a₂ – a₁ = 7 – 2 = 5; n = 10
S_n = \(\frac{n}{2}\) (2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\) [2 × 2 + (10 – 1) 5]
= 5 [4 + 45] = 5 × 49 = 245
∴ S₁₀ = 245.

(ii) – 37, – 33, – 29, ………….., 12 పదాలు
సాదన.
ఇచ్చిన A.P : – 37, – 33, – 29, …………, 12 పదాలు .
a = – 37; d = a₂ – a₁
= (- 33) – (- 37)
= – 33 + 37 = 4, n = 12
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₂ = \(\frac{12}{2}\) [2 × (- 37) + (12 – 1)4]
= 6[- 74 + 11 × 4]
= 6[- 74 + 44] = 6 (- 30) = – 180
∴ S₁₂ = – 180.

(iii) 0.6, 1.7, 2.8, …………… 100 పదాలు.
సాదన.
ఇచ్చిన A.P : 0.6, 1.7, 2.8, ….. 100 పదాలు.
a = 0.6, d = a₂ – a₁ = 1.7 – 0.6 = 1.1, n = 100
S_n = \(\frac{n}{2}\) (2a + (n – 1)d]
S₁₀₀ = \(\frac{100}{2}\) [2 × 0.6 + (100 – 1) × 1.1]
= 50 [1.2 + 99 × 1.1]
= 50[1.2 + 108.9]
= 50 × 110.1 = 5505
∴ S₁₀₀ = 5505.

(iv) \(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\), ………….., 11 పదాలు.
సాధన.
ఇచ్చిన A.P: \(\frac{1}{15}\), \(\frac{1}{12}\), \(\frac{1}{10}\), ………….., 11 పదాలు.
a = \(\frac{1}{15}\);
d = \(\frac{1}{12}\) – \(\frac{1}{15}\)
= \(\frac{5-4}{60}=\frac{1}{60}\)
n = 11
S_n = \(\frac{n}{2}\)[2a + (n – 1)d]
S₁₁ = \(\frac{11}{2}\) [2 × \(\frac{1}{15}\) + (11 – 1) × \(\frac{1}{60}\)]

= \(\frac{11}{2}\left[\frac{2}{15}+\frac{10}{60}\right]\)

= \(\frac{11}{2}\left[\frac{2}{15}+\frac{1}{6}\right]\)

= \(\frac{11}{2}\left[\frac{4+5}{30}\right]\)

= \(\frac{11}{2} \times \frac{9}{30}=\frac{33}{20}\)
∴ S₁₁ = \(\frac{33}{20}\).

ప్రశ్న 2.
క్రింది వాని మొత్తాలను కనుగొనుము.
(i) 7 + 10\(\frac{1}{2}\) + 14 + ……….. + 84
సాధన.
ఇచ్చిన A.P : 7, 10\(\frac{1}{2}\), 14, ………. 84
∴ a = 7; d = a₂ – a₁ = 10\(\frac{1}{2}\) – 7 = 3\(\frac{1}{2}\)
d = 7\(\frac{1}{2}\); a_n = 84
a_n = a + (n – 1) d = 84
= 7 + (n – 1)(\(\frac{7}{2}\)) = 84
⇒ (n – 1) × \(\frac{7}{2}\) = 84 – 7
⇒ (n – 1) \(\frac{7}{2}\) = 77
⇒ n – 1 = 77 × \(\frac{7}{2}\)
⇒ n – 1 = 22
⇒ n = 22 + 1 = 23
S_n = \(\frac{n}{2}\) [a + a_n]
S₂₃ = \(\frac{23}{2}\) [7 + 84]
= \(\frac{23}{2}\) (91)
= \(\frac{2093}{2}\) = 1046 \(\frac{1}{2}\)
∴ S₂₃ = 1046\(\frac{1}{2}\)

(లేదా)

S_n = [2a + (n – 1)d]
S₂₃ = \(\frac{23}{2}\) [2(7) + (23 – 1) \(\frac{7}{2}\)]
S₂₃ = \(\frac{23}{2}\) [14 + 22 × \(\frac{7}{2}\)]
= \(\frac{23}{2}\) [14 + 77]
= \(\frac{23}{2}\) (91)
= \(\frac{2093}{2}\)
∴ S₂₃ = 1046 \(\frac{1}{2}\).

(ii) 34 + 32 + 30 + … + 10
సాధన.
ఇచ్చిన A.P : 34, 32, 30, ………, 10
a = 34; d = a₂ – a₁ = 32 – 34 = – 2,
a_n = 10
a_n = a + (n – 1) d = 10 :
⇒ 34 + (n – 1) (- 2) = 10
⇒ 34 – 2n + 2 = 10
⇒ – 2n = 10 – 36 = – 26
⇒ 2n = 26
n = \(\frac{26}{2}\) = 13
S_n = \(\frac{n}{2}\) [a + a_n]
S₁₃ = \(\frac{13}{2}\) [34 +10] = \(\frac{13}{2}\) × 44
∴ S₁₃ = 286.

(లేదా)

S_n = \(\frac{n}{2}\) [2a + (n – 1)]
= \(\frac{13}{2}\) [2(34) + (13 – 1) (- 2)]
= \(\frac{13}{2}\) [68 – 24)
= \(\frac{13}{2}\) × 44 = 286
∴ S₁₃ = 286.

(iii) – 5 + (- 8) + (- 11) + ……….. + (- 230)
సాధన.
ఇచ్చిన A.P:
(5) + (- 8) + (- 11) + ………….. + (- 230)
a = – 5,
d = a₂ – a₁ = (- 8) – (- 5). = – 8 + 5 = – 3,
a_n = – 230
a_n = a + (n – 1) d = – 230
(- 5) + (n – 1) × (- 3) = – 230
– 5 – 3n + 3 = – 230
– 3n = – 230 + 2
– 3n = – 228
⇒ 3n = 228
n = \(\frac{228}{3}\) = 76
S_n = \(\frac{n}{2}\) [(- 5) + (- 230)]
∴ S₁ = 35 × (- 235) = – 8930
(లేదా)
S_n = \(\frac{n}{2}\) [2a + (n – 1]d]
S₇₆ = \(\frac{76}{2}\) [2(- 5) + 75(- 3)]
= 38 [- 10 – 225]
= 38 × (- 235)
∴ S₇₆ = – 8930.

ప్రశ్న 3.
ఒక అంకశ్రేణిలో
(i) a = 5, d = 3, a_n = 50 అయిన n మరియు S_n లను కనుగొనుము.
సాధన.
a = 5; d = 3; a_n = 50
a_n = a + (n – 1) 4 = 50
⇒ 5+ (n – 1) 3 = 50
⇒ 5 + 3n – 3 = 50
⇒ 3n = 50 – 2 = 48
⇒ n = \(\frac{48}{3}\) = 16.
S_n = \(\frac{n}{2}\) [a + a_n]
S₁₆ = \(\frac{16}{2}\) [5 + 50] = 8 × 55
∴ S₁₆ = 440.

(ii) a = 7, a₁₃ = 35 అయిన d ని మరియు S₁₃ ను కనుగొనుము.
సాధన.
a = 7, a_n = 35
a₁₃ = a + 12d = 35
⇒ 12d = 35 – 7 = 28
⇒ d = \(\frac{28}{12}\) = \(\frac{7}{3}\)
S_n = \(\frac{n}{2}\) [a + a_n]
S₁₃ = \(\frac{13}{2}\) [7 + 35]
= \(\frac{13}{2}\) × 42 = 13 × 21 = 273
∴ S₁₃ = 273.

(iii) a₁₂ = 37, d = 3 అయిన a ను మరియు S₁₂ ను కనుగొనుము.
సాధన.
a₁₂ = 37, d = 3
a₁₂ = a + 11d = 37
a + 11 (3) = 37
a + 33 = 37 ⇒ a = 37 – 33 = 4
S_n = \(\frac{n}{2}\) [a + a_n ]
S₁₂ = \(\frac{12}{2}\) [4 + 37] = 6 × 41 = 246
∴ S₁₂ = 246.

(iv) a₃ = 15, S₁₀ = 125 అయిన d మరియు a₁₀ లను కనుగొనుము.
సాధన.
a₃ = 15, S₁₀ = 125
a₃ = a + 2d = 15 …………. (1)
S₁₀ = \(\frac{10}{2}\) [2a + (10 – 1)d] = 125
= 2a + 9d = \(\frac{125}{2}\)
2a + 9d = 25 ……………….(2)

d = -1 ను (1) లో రాయగా,
a + 2(- 1) = 15
a = 15 + 2 = 17
a₁₀ = a + 9d = 17 + 9 (- 1)
= 17 – 9 = 8
∴ d = – 1 మరియు a₁₀ = 8.

(v) a = 2, d = 8, S_n = 90 అయిన n మరియు a_n లను కనుగొనుము.
సాధన.
a = 2; d = 8, S_n = 90
S_n = \(\frac{n}{2}\) [2a + (n – 1)d] = 90
\(\frac{n}{2}\) [2(2) + (n – 1) 8] = 90
n [4 + 8n – 8] = 90 × 2 = 180
8n² – 4n – 180 = 0
4[2n² – n -45] = 0
2n² – n – 45 = 0
2n² – 10n + 9n – 45 = 0 (∵ 2 × – 45 = – 90)
2n [n – 5] + 9 [n – 5] = 0
(n – 5) (2n + 9) = 0
∴ n – 5 = 0 లేదా 2n + 9 = 0
పదాల సంఖ్య ఎల్లప్పుడు ఒక సహజసంఖ్య.
∴ n – 5 = 0 ⇒ n = 5
∴ a₅, = a + 4d = 2 + 4(8)
= 2 + 32 = 34
∴ n = 5 మరియు a₅ = 34.

(లేదా)

S₅ = \(\frac{5}{2}\) [2 + a₅] = 90 [∵ S_n = (a + a_n)]
= 2 + a₅ = 90 × \(\frac{2}{5}\) = 36
a₅ = 36 – 2 = 34 .

(vi) a_n = 4, d = 2, S_n = – 14, అయిన n మరియు a లను కనుగొనుము.
సాధన.
a = 4, d = 2, S_n = – 14
a_n = a + (n – 1) d = 4
= a + (n – 1) (2) = 4.
∴ a + 2n = 4 + 2 = 6
a = 6 – 2n, ………… (1)
S_n = \(\frac{n}{2}\) [2a + (n – 1) d] = – 14
\(\frac{n}{2}\) [2a + (n – 1) (2)] = – 14
\(\frac{n}{2}\) × 2[a + n – 1) = – 14
n [6 – 2n + n – 1] = – 14 [(1) నుండి]
n [5 – n] = – 14
5n – n² = – 14
n² – 5n = 14
⇒ n² – 5n – 14 = 0
n² – 7n + 2n – 14 = 0 (∵ 1 × (- 14) = – 14)
n (n – 7) + 2 (n – 7) = 0
(n – 7) (n + 2) = 0
పదాల సంఖ్య n ఎల్లప్పుడు ఒక సహజ సంఖ్య.
∴ n – 7 = 0
n = 7
n = 7 ను (1) లో ప్రతిక్షేపించగా,
a = 6 – 2 (7) = 6 – 14 = – 8
∴ n = 7, a = – 8.

(vii) l = 28, S = 144 మరియు పదాల సంఖ్య 9 అయిన a విలువ కనుగొనుము.
సాధన.
l = a_n = 28, S = 144 మరియు n = 9.
[∵ A.P. లో చివరి పదాన్ని l తో సూచిస్తారు]
S_n = \(\frac{n}{2}\) [a + a_n] = 144
\(\frac{9}{2}\) [a + 28] = 144
a + 28 = 144 × 2
a + 28 = 32
a = 32 – 28 = 4
∴ a = 4.

ప్రశ్న 4.
ఒక అంకశ్రేణిలో మొదటి, చివరి పదాలు వరుసగా 17 మరియు 350. సామాన్య భేదం 9 అయిన శ్రేణిలోని పదాల సంఖ్యను, పదాల మొత్తమును కనుగొనుము.
సాధన.
ఒక అంకశ్రేఢిలో మొదటి పదం a = 17
చివరి పదం a_n = 350
సామాన్యభేదం d = 9
a_n = a + (n – 1) 4 = 350
17 + (n – 1) 9 = 350
17 + 9n – 9 = 350
9n + 8 = 350
9n = 350 – 8 = 342
n = \(\frac{342}{9}\) = 38
∴ n = 38.
ఇప్పుడు S_n = \(\frac{n}{2}\) [a + a_n]
S₃₈ = \(\frac{38}{2}\) [17 + 350] = 19 × 367
S₃₈= 6973
∴ పదాల సంఖ్య n = 38
38 పదాల మొత్తం S₃₈ = 6973.

ప్రశ్న 5.
ఒక అంకశ్రేణిలో 2వ, 3వ పదాలు వరుసగా 14 మరియు 18 అయిన 51 పదాల మొత్తమును కనుగొనుము.
సాధన.
ఒక అంకశ్రేణిలో
2వ పదం a₂ = a + 4 = 14 ………… (1)
3వ పదం a₃ = a + 2d = 18 …………..(2)
పదాల సంఖ్య = 51
d = a₂ – a₁ = 18 – 14 = 4
d ను (1) లో రాయగా
a + 4 = 14 = a = 14 – 4 = 10
a = 10, d = 4, n = 51 అయిన
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₅₁ = \(\frac{51}{2}\) [2 × 10 + (51 – 1) × 4) |
= \(\frac{51}{2}\) [20 + 50 × 4]
= \(\frac{51}{2}\) × (20 + 200)
= \(\frac{51}{2}\) × 220
= 51 × 110 = 5610
∴ 51 పదాల మొత్తం S_n = 5610.

ప్రశ్న 6.
ఒక అంకశ్రేఢిలో మొదటి 7 పదాల మొత్తము 49 మరియు 17 పదాల మొత్తము 289 అయిన మొదటి n పదాల మొత్తమును కనుగొనుము.
సాధన.
S₇ = 49 మరియు S₁₇ = 289
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₇ = \(\frac{7}{2}\) [2a + (7 – 1)d] = 49 .
= \(\frac{7}{2}\) [2a + 6d] = 49
2a + 6d = 49 × \(\frac{2}{7}\) = 14
∴ 2a + 6d = 14 ………. (1)
అలాగే S₁₇ = \(\frac{17}{2}\) [2a + 16d] = 289
2a + 16d = 289 × \(\frac{2}{27}\) = 34
∴ 2a + 16d = 34 ………. (2)

d = 2 ను (1) లో ప్రతిక్షేపించగా,
2a + 6(2) = 14
2a = 14 – 12 = 2
∴ a = \(\frac{2}{2}\) = 1
a = 1, d = 2 అయిన S_n
S_n = \(\frac{n}{2}\) [2 (1) + (n – 1) 2]
= \(\frac{n}{2}\) [2 + 2n – 2]
= \(\frac{n}{2}\) × 2n
S_n = n²
[Shortcut:-
S_n = 49 = 7²
S_n = 289 = 17²
S_n = n²
∴ మొదటి n పదాల మొత్తం S_n = n².

ప్రశ్న 7.
a_n క్రింది విధంగా నిర్వచించబడితే a₁, a₂, ………., a_n, అంకశ్రేణి అవుతుందని చూపండి. మరియు మొదటి 15 పదాల మొతమును కనుగొనండి.
(i) a_n = 3 + 4n
(ii) a_n = 9 – 5n
సాధన.
(i) a_n = 3 + 4n
a₁ = 3 + 4(1) = 7
a₂ = 3 + 4(2) = 3 + 8 = 11
a₃ = 3 + 4(3) = 3 + 12 = 15
a₄ = 3 + 4 (4) = 3 + 16 = 19
…………………………………………………………..
………………………………………………………….
a₁, a₂, a₃, …………… = 7, 11, 15, 19, ……………
d = a₂ – a₁ = 11 – 7 = 4
d = a₃ – a₂ = 15 – 11 = 4
d = a₄ – a₃ = 19 – 15 = 4
అన్ని సందర్భాలలోను , సమానము. కావున a₁, a₂, a₃, a₄, ….., a_n అంకశ్రేణి అవుతుంది.
15 పదాల మొత్తం a = 7, d = 4, n = 15
S₁₅ = \(\frac{15}{2}\) [2x 7 + (15 – 1) 4]
[∵ S_n = \(\frac{n}{2}\) [2a + (n – 1) d]]
= \(\frac{15}{2}\) (14 + 14 × 4]
= \(\frac{15}{2}\) [70]
= 15 × 35 = 525
∴ 15 పదాల మొత్తం S₁₅ = 525.

(ii) a_n = 9 – 5n
సాధన.
a₁ = 9 – 5 × 1= 9 – 5 = 4
a₂ = 9 – 5 × 2 = 9 – 10 = – 1
a₃ = 9 – 5 × 3 = 9 – 15 = – 6
a₄ = 9 – 5 × 4 = 9-20 = – 11
………………………………..
a₁, a₂, a₃, a₄ ………….. = 4, – 1, – 6, – 11, ……………
d = a₂ – a₁ = – 1 – 4 = – 5
d = a₃ – a₂ = – 6 – (- 1) = – 6 + 1 = – 5
d = a₄ – a₃ = – 11 -(- 6) = – 11 + 6 = – 5
………………………………………………..
………………………………………………..
అన్ని సందర్భాలలోను d సమానము. కావున a₁, a₂, a₃, a₄, …………… a_n అంకశ్రేఢి అవుతుంది.
15 పదాల మొత్తం a = 4, d = – 5, n = 15
S₁₅ = 15 [2(4) + (15 – 1) (- 5)]
= 15 [8 + 14 (- 5)]
= \(\frac{15}{2}\) × – 62 = 15 × – 31 = – 465
∴ 15 పదాల మొత్తం S₁₅ = 465.

ప్రశ్న 8.
ఒక అంకశ్రేణిలో మొదటి n పదాల మొత్తము 4n – na అయిన మొదటి పదం ఎంత ? (S, విలువే మొదటి పదము అవుతుందని గుర్తుకు తెచ్చుకోండి) మొదటి రెండు పదాల మొత్తం ఎంత ? రెండవ పదము ఎంత ? అదేవిధంగా 8వ పదమును, 10వ పదమును మరియు nవ పదమును కనుగొనుము.
సాధన.
మొదటి పద్దతి : 2
ఒక అంకశ్రేణిలో n పదాల మొత్తం S_n = 4n – na
మొదటిపదం a₁ = S₁ = 4 (1) – (1)² = 3
మొదటి రెండు పదాల మొత్తం S₂ = 4 (2) – (2)²
= 8 – 4 = 4
రెండవ పదం a₂ = S₂ – S₁ = 4 – 3 = 1
మొదటి మూడు పదాల మొత్తం S₃ = 4 x (3) – (3)²
= 12 – 9 = 3
మూడవ పదం a₃ = S₃ – S₂ = 3 – 4 = – 1
మొదటి తొమ్మిది పదాల మొత్తం S₉ = 4(9) – 9²
= 36 – 81 = – 45
మొదటి పది పదాల మొత్తం S₁₀ = 4(10) – 10²
= 40 – 100 = – 60
పదవ పదము = a₁₀ = S₁₀ – S₉
= – 60 – (- 45)
= – 60 + 45 = – 15
(n – 1) పదాల మొత్తం S_{n – 1}
= 4 (n – 1) – (n – 1)²
= 4n – 4 – (n² – 2n + 1)
= 4n – 4 – n² + 2n -1
S_{n – 1} = 6n – n² – 5
n పదాల మొత్తం S_n = 4n – n²
∴ n వ పదం a_n = S_n – S_{n – 1}
= (4n – n²) – (6n – n² – 5) ..
= 4n -n² – 6n + n² + 5
a_n = 5 – 2n.

రెండవ పద్ధతి :
అంకశ్రేణి n పదాల మొత్తం S_n = 4n – n²
మొదటి పదం a₁ = S₁ = 4(1) – (1)2²
= 4 – 1 = 3
మొదటి రెండు పదాల మొత్తం S₂ = 4(2) – (2)²
=8 – 4 = 4
రెండవ పదం a₂ = S₂ – S₁ = 4 – 3 = 1
∴ సామాన్యభేదం d = a₂ – a₁ = 1 – 3 = – 2
∴ మూడవపదం a₃ = a₂ + d = 1 + (- 2) = – 1
పదవపదం a₁₀ = a + 9d = 3 + 9 (- 2)
= 3 – 18 = – 15
n వ పదము a_n = a + (n- 1) d
= 3 + (n – 1) (- 2)
= 3 – 2n + 2
a_n = 5 – 2n

మూడవ పద్ధతి :
అంకశ్రేణిలో S_n = 4n – n²
nవ పదం a_n = S_n – S_{n – 1} అవుతుంది.
S_{n – 1} = 4 (n – 1) – (n – 1)
= 4n -4 – (n² – 2n + 1)
= 4n – 4 – n² + 2n – 1
S_{n – 1} = 6n – n² – 5
a_n = S_n – S_{n – 1}
= (4n – n²) – (6n – n² – 5)
= 4n – n² – 6n + n² + 5
a_n = 5 – 2n
∴ మొదటి పదం a₁ = 5 – 2(1) = 3
మొదటి రెండు పదాల మొత్తం S₂ = 4(2) – 2²
= 8 – 4 = 4
a₂ = 5 – 2(2) = 5 – 4 = 1
a₃ = 5 – 2(3) = 5 – 6 = – 1
a_n = 5 – 2(10) = 5 – 20 = – 15
nవ పదం a_n = 5 – 2n.

ప్రశ్న 9.
6చే భాగించబడే మొదటి 40 ధనపూర్ణ సంఖ్యల మొత్తమును కనుగొనుము.
సాధన.
6 చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యల జాబితా 6, 12, 18, 24, …….. 40 పదాలు .
ఈ జాబితా అంకశ్రేణిలో కలదు.
a = 6, d = a₂ – a₁ = 12 – 6 = 6, n = 40
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₄₀ = \(\frac{40}{2}\) [2(6) + (40 – 1) (6)]
= 20 [12 + 39 × 6]
= 20 [12 + 234] = 20 × 246
S₄₀ = 4920.
6చే భాగింపబడే మొదటి 40 ధనపూర్ణ సంఖ్యల, మొత్తం S₄₀ = 4920.

ప్రశ్న 10.
ఒక పాఠశాలలో విద్యావిషయక సంబంధిత విషయాలలో అత్యున్నత ప్రతిభ కనపరిచిన వారికి మొత్తం 700 రూపాయలకు 7 బహుమతులు ఇవ్వాలని భావించారు. ప్రతి బహుమతి విలువ దాని ముందున్న దానికి ₹ 20 తక్కువ అయిన ప్రతి బహుమతి విలువను కనుగొనుము.
సాధన.
బహుమతులను a₁, a₂, a₃, a₄, a₅, a₆, a₇, ………………. అనుకొనుము.
ప్రతి బహుమతి దాని ముందున్న బహుమతికన్నా ₹ 20 తక్కువ.
కావున, a₁, a₂, a₃, a₄, ….., a₇ లు Sn A.P. లో ఉంటాయి.
∴ సామాన్యభేదం d = a₂ – a₁ = – 20
(∵ a₁ కన్నా a₂, 20 తక్కువగా ఉంటుంది.)
లెక్క ప్రకారం బహుమతుల మొత్తం S₇ = 700 .
S₇ = \(\frac{7}{2}\) [2a + (7 – 1) (- 20)] = 700
[2a + 6 (- 20)] = 700 × \(\frac{2}{7}\)
2a – 120 = 200
2a = 200 + 120 = 320
a = \(\frac{320}{2}\) = 160
∴ బహుమతుల విలువ a = a₁ = 160
a₂ = 160 – 20 = 140
a₃ = 140 – 20 = 120
a₄ = 120 – 20 = 100
a₅ = 100 – 20 = 80
a₆ = 80 – 20 = 60
a₇ = 60-20 = 40.

ప్రశ్న 11.
ఒక పాఠశాల ఆవరణలో పర్యావరణ పరిరక్షణకు విద్యార్థులు చెట్లు నాటాలని భావించారు. ప్రతి సెక్షను విద్యార్థులు వారు చదువుతున్న తరగతి సంఖ్యకు సమానమైన చెట్లను అనగా 1వ తరగతి చదువుచున్న ఒక సెక్షన్ విద్యార్థులు 1 చెట్టును, రెండవ తరగతి చదువుచున్న ఒక సెక్షన్ విద్యార్థులు 2 చెట్లను నాటాలని ఈ విధంగా 12వ తరగతి వరకూ చేయాలని నిర్ణయించుకున్నారు. అయితే ప్రతి తరగతిలో మూడు సెక్షన్లు ఉన్న మొత్తం నాటిన చెట్లు ఎన్ని?
సాధన.

మూడు సెక్షన్ల విద్యార్థులు నాటే చెట్ల సంఖ్య జాబితా 3, 6, 9, 12, ………….. 33, 36.
ఇది A.P లో కలదు.
12 తరగతులలోని మూడు సెక్షన్ల విద్యార్థులు నాటిన మొత్తం చెట్లు = 3 + 6, + 9 +:12 + …. + 36
a = 3, 4 = 6 – 3 = 3, n = 12
∴ S₁₂ = \(\frac{12}{2}\) [3 + 36]
[∵ S_n = \(\frac{n}{2}\) [a +1]].
= 6 × 39.
S₁₂ = 234
∴ ప్రతి తరగతిలోని మూడు సెక్షన్ల విద్యార్థులు నాటిన మొత్తం చెట్లు = 234.

రెండవ పద్ధతి :
ప్రతి తరగతిలోని ఒక సెక్షన్ విద్యార్థులు నాటిన చెట్ల సంఖ్య జాబితా 1, 2, 3, 4, 5, 6, ………… 11. 12 ఇది A.P లో కలదు.
ప్రతి తరగతిలోని ఒక సెక్షన్ విద్యార్థులు నాటిన మొత్తం చెట్లు = 1 + 2 + 3 + ………….. + 11 + 12
a = 1, d = 1, n = 12 S₁₂ = \(\frac{12}{2}\) [1 + 12]
= 6 × 13 = 78 [∵ S_n = \(\frac{n}{2}\) [a + a_n]]
ప్రతి తరగతిలోని ఒక సెక్షన్ విద్యార్థులు నాటిన మొత్తం చెట్లు = 78
ప్రతి తరగతిలోని మూడు సెక్షన్ల విద్యార్థులు నాటిన మొత్తం చెట్లు = 78 × 3 = 234.

ప్రశ్న 12.
అర్ధ వృత్తాలచే ఒక సర్పిలాకారము తయారుచేయబడింది. పటంలో చూపిన విధంగా అర్ధవృత్తాల కేంద్రాలు A వద్ద ప్రారంభించబడి A, Bల మధ్య మారుతూ వున్నాయి. అనగా మొదటి అర్ధవృత్త కేంద్రము A, రెండవ అర్ధవృత్త కేంద్రము B, మూడవ అర్ధవృత్త కేంద్రము A …… మరియు అర్ధవృత్తాల వ్యాసార్ధాలు వరుసగా 0.5 సెం.మీ., 1.0 సెం.మీ, 1.5 సెం.మీ, 20 సెం.మీ, … ఈ విధంగా మొత్తం 18 అర్ధవృత్తాలు వున్న సర్పిలం మొత్తం పొడవు ఎంత ? (x = 4) (సూచన : వరుస అర్ధవృత్తాల పొడవులు l₁, l₂, l₃, l₄ . . . మరియు వీని కేంద్రాలు వరుసగా A, B, A, B……..]

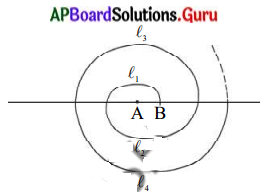
సాధన.
వరుస అర్ధవృత్తాల పొడవులు l₁, l₂, l₃, l₄, ……. మరియు వీటి కేంద్రాలు A, B, A, B
అర్ధవృత్తాల వ్యాసార్ధాలు వరుసగా 0, 5 సెం.మీ., 1 సెం.మీ., 1, 5 సెం.మీ., 2 సెం.మీ…
l₁ = π(0.5) = 0.5π (∵ అర్ధవృత్త చాపం పొడవు l = πr)
l₂ = π(1) = π
l₃ = π(1.5) = 1.5π
l₄ = π(2) = 2π
……………………
…………………………
l₁, l₂, l₃, l₄, ……. లు A.P. లో కలవు.
13 అర్ధవృత్తాలు గల సర్పిలం మొత్తం పొడవు l₁, l₂, l₃, l₄, …………..l₁₃
0.5π + π + 1.5π + ……….. + 13 పదాలు ……… (1)
a = 0.5π, d = 0.57 మరియు n = 13
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₃ = \(\frac{13}{2}\) [2(0.5π) + ( 13 – 1) (0.5π)]
= \(\frac{13}{2}\) [π + 6π] = 13 × 7π
= \(\frac{13}{2}\) × 7 × \(\frac{22}{7}\) = 13 × 11
S₁₃ = 143 సెం.మీ.
∴ 13 అర్ధవృత్తాలున్న సర్పిలం మొత్తం పొడవు = 143 సెం.మీ.

(లేదా)
(1) ⇒ π (0.5 + 1 + 1.5 + 2 + ……… + 13 పదాలు )
S₁₃ = π [\(\frac{13}{2}\) (2 (0.5) + (13 – 1) (0.5)]
= π [\(\frac{13}{2}\) (1 + 6)]
= \(\frac{22}{7}\) × \(\frac{13}{2}\) × 7 = 11 × 13
S₁₃ = 143 సెం.మీ.

 

ప్రశ్న 13.
200 చెక్క మొద్దులను క్రింది పటంలో చూపిన విధంగా అమర్చారు. అన్నింటి కంటే క్రింద వున్న వరుసలో 20 చెక్క మొద్దులను, దానిపై 19 మొద్దులను, దాని పైన 18 మొద్దులను ….. అమర్చిన మొత్తం 200 మొద్దులను అమర్చుటకు ఎన్ని వరుసలు కావాలి ? అన్నింటికంటే పైన వున్న వరుసలో ఎన్ని చెక్క మొద్దులు కలవు ?

సాధన.
క్రింది నుండి ప్రతి వరుసలోను గల చెక్క మొద్దుల సంఖ్య జాబితా 20, 19, 18, 17, ……. ఇది A. P. లో కలదు.
a = 20, d = a₂ – a₁ = 19 – 20 = -1
మొత్తం చెక్క మొద్దుల సంఖ్య S_n = 200
S_n = \(\frac{n}{2}\) [2a + (n – 1) d] = 200
\(\frac{n}{2}\) [2(20) + (n – 1) (- 1)] = 200
\(\frac{n}{2}\) [40 – n+1] = 200
\(\frac{n}{2}\) [41 – n] = 200
41n – n² = 400
⇒41n – n² – 400 = 0
⇒ n² – 41n + 400 = 0
⇒ n² – 25n – 16n + 400 = 0 ( 1 × 400 = 400)

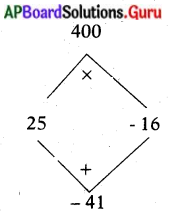
⇒ n (n – 25) – 16 (n – 25) = 0.
⇒ (n – 25) (n – 16) = 0
∴ n – 25 = 0 లేదా n – 16 = 0
n = 25 లేదా n = 16
n = 25 అసాధ్యము. కావున n = 16
(20, 19, 18, ……. జాబితాలో 25వ పదం రుణసంఖ్య అవుతుంది.)
అనగా ’20, 19, 18, …… శ్రేణిలో 16 పదాలుంటాయి. కావున 200 మొద్దులను అమర్చుటకు 16 వరుసలు కావాలి.
పై వరుసలోని మొద్దుల సంఖ్య = a₁₆ = a + 15d = 20 + 15(- 1) = 20 – 15 = 5
∴ పై వరుసలోని మొద్దుల సంఖ్య = 5. – A.P. 10వ తరగతి జీ గణితశాస్త్రం

ప్రశ్న 14.
బంతి మరియు బకెట్ ఆటలో, ప్రారంభంలో ఒక బకెట్ దానికి 5మీ. దూరంలో ఒక బంతి ఉంచబడినవి. మొత్తం 10 బంతులలో మిగిలిన బంతులు ఒకదానికొకటి 3మీ. దూరంలో పటంలో చూపిన విధంగా అమర్చబడినవి. ఆటలో పాల్గొనే వ్యక్తి మొదట బకెట్ వద్ద నుంచి బయలుదేరి మొదటి బంతివద్దకు పోయి దానిని తీసుకొని వెనుకకు వచ్చి ‘బకెట్లో వేయాలి. తరువాత తిరిగి బకెట్ నుంచి బయలుదేరి రెండవ బంతి వద్దకు పోయి దానిని తీసుకొని వచ్చి బకెట్లో వేయాలి. ఈ విధంగా అన్ని బంతులను బకెట్లో వేయవలెనన్న ఆ వ్యక్తి పరిగెత్తవలసిన మొత్తం దూరం ఎంత ? (సూచన : మొదటి, రెండవ బంతులను తీసుకొని రావడానికి ఆట ఆడే వ్యక్తి పరిగెత్తవలసిన దూరము వరుసగా 2 × 5 + 2 × (5 + 3)]

సాధన.

ప్రతి బంతి తీసుకురావడానికి వ్యక్తి ప్రయాణించిన దూరాల జాబితా 10, 16, 22, 28, …………….. 10 పదాలు.
ఇది A.P. లో కలదు.
a = 10; 4 = 16 – 10 = 6, n = 10.
∴ వ్యక్తి పరుగెత్తిన మొత్తం దూరం 10 + 16 + 22 + 28 + ……….. + 10 పదాలు.
S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₁₀ = \(\frac{10}{2}\) [2 × 10 + (10 – 1) × 6] = 5[20 + 54] = 5 × 74
S₁₀ = 370
∴ వ్యక్తి పరుగెత్తిన మొత్తం దూరం = 370 మీ.