AP Board 10th Class Maths Solutions Chapter 6 శ్రేఢులు Exercise 6.2

SCERT AP 10th Class Maths Textbook Solutions Chapter 6 శ్రేఢులు Exercise 6.2 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 6th Lesson శ్రేఢులు Exercise 6.2

ప్రశ్న 1.
మొదటి పదము a, సామాన్య భేదము d, nవ పదము a, అయిన క్రింది పట్టికను పూరింపుము. – AS,, AS,,

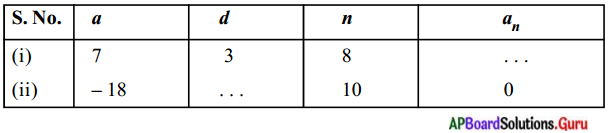
సాధన.

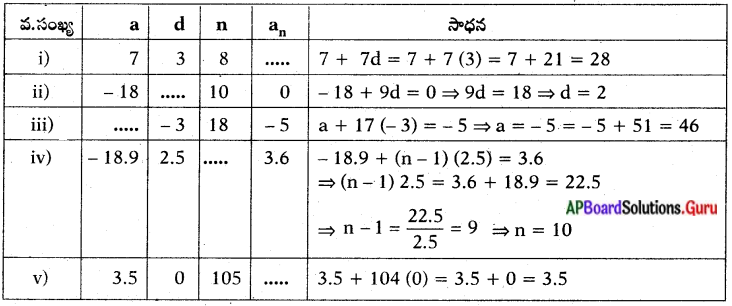
ప్రశ్న 2.
కింది వానిని కనుగొనుము.
(i) 10, 7, 4, …… అంకశ్రేణిలో 30వ పదము.
సాధన.
ఇచ్చిన A.P. = 10, 7, 4, …………….
a₁ = 10;
d = a₂ – a₁ = 7 – 10 = – 3,
n= 30
a_n = a + (n – 1)
a₃₀ = 10 + (30 – 1) (- 3)
= 10 + 29 (- 3)
= 10 – 87 = – 77
∴ a₃₀ = – 77.

(ii) – 3, \(-\frac{1}{2}\), – 2, ………….. అంకశ్రేణిలో 11వ పదము.
సాధన.
ఇచ్చిన A.P. = – 3, \(-\frac{1}{2}\), – 2, …………..
a = – 3; d = a₂ – a₁ = 3 – 3)
= \(-\frac{1}{2}\) + 3 = 2\(\frac{1}{2}\) = \(\frac{5}{2}\)
n = 11
∴ a_n = a + (n – 1) d
a₁₁ = – 3 + (11 – 1) (\(\frac{5}{2}\))
= – 3 + 10(\(\frac{5}{2}\))
= – 3 + 25 = 22
∴ a₁₁ = 22.

ప్రశ్న 3.
క్రింది వానిని కనుగొనుము.
(i) a₁ = 2; a₃ = 26, అయిన a₂ ను కనుగొనుము.
సాధన.
మొదటి పద్ధతి :
a₁ = a = 2
a₃ = 26
a_n = a + (n – 1) d
a₃ = 2 + (3 – 1) 4
= 2d= 26 – 2 = 24
d = \(\frac{24}{2}\) = 12
∴ a₂ = a + d = 2 + 12 = 14.

రెండవ పద్ధతి :
a₁, a₂, a₃ లు A.P. లో కలవు అనుకొనుము.
లెక్క ప్రకారం a₁ = 2, a₃ = 26
∴ 2, a₂, 26 లు A.P. లో కలవు.
a₂ – 2 = 26 – a₂
∴ a₂ + a₂ = 26 + 2
2a₂ = 28
∴ a₂ = \(\frac{28}{2}\) = 14.

మూడవ పద్ధతి :
a, b, c లు A.P. లో ఉంటే b = \(\frac{a+c}{2}\)
2, a₂, 26 లు A.P. లో కలవు.
∴ a₂ = \(\frac{2+26}{2}\) = \(\frac{28}{2}\) = 14.

(ii) a₂ = 13; a₄ = 3 అయిన a₁, a₃ లను కనుగొనుము.
సాధన.
మొదటి పద్ధతి :
a₂ = a + d = 13 …….. (1)
a₄ = a + 3d = 3 …….. (2)
(1), (2) సమీకరణములు సాధించగా,

⇒ d = \(-\frac{10}{2}\) = – 5
a₁ = a₂ – d = 13 – (-5) = 13 + 5 = 18
a₃ = a₂ + d = 13 + (- 5) = 8
∴ a₁ = 18 మరియు a₃ = 8.

రెండవ పద్ధతి :
a₁, a₂, a₃, a₄ లు A.P. లో కలవు అనుకొనుము.
లెక్క ప్రకారము a₂ = 13, a₄ = 3
∴ a₁, 13, a₃, 3 లు A.P. లో కలవు
∴ 13 – a₁ = a₃ – 13 ……. (1) మరియు
a₃ – 13 = 3 – a₃ ……….. (2)
(2) ⇒ 2a₃ = 16
a₃ = \(\frac{16}{2}\) = 8
a₃ = 8 ని (1) లో రాయగా,
13 – a₁ = 8 – 13
– a₁ = – 5 – 13 = – 18
∴ a₁ = 18
∴ a₁ = 18 మరియు a₃ = 8.

మూడవ పద్ధతి :
a₁, 13, a₃, 3 లు A.P. లో కలవు.
∴ 13, a₃, 3 లు A.P. లో మూడు వరుస పదాలు.
∴ a₃ = \(\frac{13+3}{2}=\frac{16}{2}\) = 8
[a, b, c లు A.P. లో ఉంటే b = \(\frac{a+c}{2}\))
∴ సామాన్య భేదం d = a₃ – a₂ = 8 – 13 = – 5
∴ a₁ = a₂ – d = 13 – (- 5) = 13 + 5 = 18.
∴ a₁ = 18 మరియు a₃ = 8.

(iii) a₁ = 5, a₄ = 91/2 అయిన a₂, a₃ లను కనుగొనుము.
సాధన.
a₁ = a = 5.
a_n = a + (n – 1) d
a₄ = 5 + 3d = 9\(\frac{1}{2}\) = \(\frac{19}{2}\)
3d = \(\frac{19}{2}\) – 5 = \(\frac{19-10}{2}\) = \(\frac{9}{2}\)
∴ d = \(\frac{9}{2} \times \frac{1}{3}=\frac{3}{2}\)
∴ a₂ = a + d
= 5 + \(\frac{3}{2}\) = \(\frac{13}{2}\)
a₃ = a₂ + d
= \(\frac{13}{2}\) + \(\frac{3}{2}\) = \(\frac{16}{2}\) = 8

(iv) a₁ = – 4; a₆ = 6, అయిన a₂, a₃, a₄, a₅ లను కనుగొనుము. .
సాధన.
మొదటి పద్ధతి :
a₁ = a = – 4
a₆ = a + 5d = 6
(- 4) + 5d = 6
⇒ 5d = 6 + 4 = 10
⇒ d = \(\frac{10}{5}\) = 2
∴ a₂ = – 4 + 2 = – 2
a₃ = – 2 + 2 = 0
a₄ = 0 + 2 = 2
a₅ = 2 + 2 = 4

రెండవ పద్దతి :
ఒక అంకశ్రేణిలో nవ పదం a_n, mవ పదం a_m అయిన సామాన్యభేదం
d = \(\frac{a_{m}-a_{n}}{m-n}\)
a₁ = – 4, a₆ = 6, n = 1; m = 6
d = \(\frac{6-(-4)}{6-1}=\frac{10}{5}\) = 2
∴ a₂ = a₁ + d = – 4 + 2 = – 2
a₃ = – 2 + 2 = 0
a₄ = 0 + 2 = 2
a₅ = 2 + 2 = 4.

(v) a₂ = 38; a₆ = – 22, అయిన a₁, a₃, a₄, a₅ లను కనుగొనుము.
సాధన.
a₂ = a + d = 38 ……………. (1)
a₆ = a + 5d = -22 …………… (2)
(2) – (1)

∴ a₁ = a₂ – d = 38 – (- 15) = 38 + 15 = 53
a₃ = a₂ + 4 = 38 + (-15) = 23
a₄ = 23 + (- 15) = 8
a₅ = 8 + (- 15) = – 7.

ప్రశ్న 4.
3, 8, 13, 18, … అంకశ్రేణిలో ఎన్నవ పదము 78 అవుతుంది ?
సాధన.
ఇచ్చిన అంకశ్రేణి : 3, 8, 13, 18, ……. 78 –
a = 3; d = a₂ – a₁ = 8 – 3 = 5,
a_n = 78
a_n = a + (n – 1) 4 = 78 .
⇒ 3 + (n – 1) (5) = 78
⇒ 3 + 5n – 5 = 78
⇒ 5n – 2 = 78
⇒ 5n = 78 + 2 = 80
⇒ n = \(\frac{80}{5}\) = 16
∴ 16 వ పదము 78 అవుతుంది.

ప్రశ్న 5.
క్రింద ఇవ్వబడిన అంకశ్రేఢులలోని పదాల సంఖ్యను కనుగొనుము.
(i) 7, 13, 19, . . . , 205
సాధన.
మొదటి పద్దతి :
ఇచ్చిన A.P : 7, 13, 19, …………, 205
a = 7; d = a₂ – a₁ = 13 – 7 = 6,
a_n = 205
a_n = a + (n – 1) d = 205
7 + (n – 1) 6 = 205
7 + 6n – 6 = 205
6n + 1 = 205
6n = 205 – 1 = 204
⇒ n = \(\frac{204}{6}\) = 34
ఇచ్చిన A.P లో 34 పదాలు ఉంటాయి.

రెండవ పద్ధతి:
d = \(\frac{a_{m}-a_{n}}{m-n}=\frac{a_{n}-a_{m}}{n-m}\)
a₁ = 7, a_n = 1, a_m = 205 అనుకొనుము.
d = 13 – 7 = 6
6 = \(\frac{205-7}{n-1}\)
⇒ n – 1 = \(\frac{198}{6}\) = 33
∴ n = 33 + 1 = 34.

(ii) 18, 15\(\frac{1}{2}\), 13, ………, – 47
సాధన. మొదటి పద్ధతి : –
ఇచ్చిన A.P: 18, 15\(\frac{1}{2}\), 1.3 ………….. – 47
a = 18, d = a₂ – a₁
= 15\(\frac{1}{2}\) – 18
= – 2\(\frac{1}{2}\) = – \(\frac{5}{2}\)
a_n = – 47
a_n = a + (n – 1) d = – 47
= 18 + (n – 1) × (- \(\frac{5}{2}\)) = – 47
(n – 1) (- \(\frac{5}{2}\)) = – 47 – 18 = – 65
\(\frac{-5 n+5}{2}\) = – 65
– 5n + 5 = – 130
– 5n = – 130 – 5 = – 135
5n = 135
⇒ n = \(\frac{135}{5}\) = 27
ఇచ్చిన A.P లో 27 పదాలు ఉంటాయి.

రెండవ పద్ధతి :
a_m = 18, d = 35; a_n = – 47
d = \(\frac{a_{n}-a_{m}}{n-m}\)

⇒ \(\frac{-5}{2}=\frac{-47-18}{n-1}\)

⇒ \(\frac{-5}{2}=\frac{-65}{n-1}\)

⇒ \(\frac{5}{2}=\frac{65}{n-1}\)
n – 1 = 65 × \(\frac{2}{5}\)
∴ n = 26 + 1 = 27.

ప్రశ్న 6.
11, 8, 5, 2… అంకశ్రేణిలో ‘- 150’ ఒక పదంగా ఉంటుందో లేదో పరిశీలించుము కనుగొనుము.
సాధన.
ఇచ్చిన అంకశ్రేణి 11, 8, 5, 2, …… లో n వ పదం – 150 అనుకుందాము.
అప్పుడు, a = 11, d = a₂ – a₁ = 8 – 11 = – 3 మరియు a_n = – 150
a_n = a + (n – 1) d = – 150
⇒ 11 + (n – 1)X (- 3) = – 150
⇒ 11 – 3n + 3 = – 150
⇒ – 3n = – 150 – 14
⇒ – 3n = – 164
⇒ 3n = 164
⇒ n = \(\frac{164}{3}\) ………… (2)
అంకశ్రేణిలోని పదాల సంఖ్య n ఎల్లప్పుడూ ఒక సహజ సంఖ్య.
కాని n = \(\frac{164}{3}\) సహజసంఖ్య కాదు.
కావున 11, 8, 5, 2, ……. అంకశ్రేణిలో – 150 ఒక పదంగా ఉండదు.

ప్రశ్న 7.
ఒక అంకశ్రేణిలో 11వ పదము 38 మరియు 16వ పదము 78 అయిన 31వ పదమును కనుగొనుము.
సాధన.
a₁₁ = 38 మరియు a₁₆ = 73, a₃₁ = ?
::. a_n = a + (n – 1) d
a₁₁ = a + 10d = 38 …………. (1)
a₁₆ = a + 15d = 73 ,
(2) – (1)

d = 7 ను (1) లో రా యగా,
a + 70 = 38
⇒ a = 38 – 70 = – 32
31వ పదం a₃₁ = a + 30d
= – 32 + 30 (7)
= – 32 + 210 = 178
∴ 31వ పదం a_n = 178.

ప్రశ్న 8.
ఒక అంకశ్రేఢిలో 3వ, 9వ పదాలు వరుసగా 4, – 8 అయిన ఎన్నవ పదము ” (సున్న) అవుతుంది ?
సాధన.
ఒక A.P లో 3వ పదం
a₃ = a + 2d = 4 ……….(1)
9వ పదం a₉ = a + 8d = – 8 …………(2)
(2) – (1) ⇒

⇒ d = \(\frac{12}{6}\) = – 2
⇒ d = – 2 …………. (3)
∴ 4వ పదం a₄ = a₃ + d = 4 + (- 2) = 2
a₅ = a₄ + d = 2 + (- 2) = 0
∴ 5వ పదం సున్న (0) అవుతుంది.

(లేదా)

(3) ⇒ d = – 2 ను (1) లో రాయగా,
a + 2(- 2) = 4
⇒ a – 4 = 4
⇒ a = 8
a_n = 0 అయ్యేటట్లు n విలువ కనుగొనాలి.
a_n = a + (n – 1) d = 0
8 + (n – 1) (- 2) = 0
8 – 2n + 2 = 0
10 = 2n
⇒ \(\frac{10}{2}\) = 5
∴ n = 5
కావున 5వ పదం ‘0’ (సున్న) అవుతుంది.

ప్రశ్న 9.
ఒక అంకశ్రేణిలో 17వ పదము 10వ పదం కంటే 7 ఎక్కువ. అయిన సామాన్య భేదం ఎంత ?
సాధన.
ఒక A.P లో 17వ పదం a₁₇ = a + 16d
10వ పదం a₁₀ = a + 9d
లెక్క ప్రకారం, a₁₇ = a₁₀ + 7
a + 16d = (a + 9d) + 7
a + 16d – a – 9d = 7
7d = 7
⇒ d = \(\frac{7}{7}\) = 1
∴ సామాన్యభేదం d = 1. .

ప్రశ్న 10.
రెండు అంకశ్రేఢుల సామాన్య భేదం సమానము. వాని 100వ పదాల మధ్య భేదం 100 అయిన వాని 1000వ పదాల మధ్య భేదమెంత ?
సాధన.
మొదటి అంకశ్రేణి మొదటి పదం = a
రెండవ అంకశ్రేణి మొదటి పదం = b
రెండు శ్రేఢుల యొక్క సామాన్యభేదం = d అనుకొనుము.
మొదటిశ్రేఢి 100వ పదం a₁₀₀ = a + 99d
రెండవశ్రేణి 100వ పదం b₁₀₀ = b + 99d
లెక్కప్రకారం, a₁₀₀ – b₁₀₀ = 100
(a + 99d) – (b + 99d) = 100
a – b = 100 ………….. (1)
ఇప్పుడు,
మొదటిశ్రేఢి 1000వ పదం a₁₀₀₀ = a + 999d
రెండవశ్రేణి’ 1000వ పదం b₁₀₀₀₀ = b + 999d
a₁₀₀₀ – b₁₀₀₀ = (a + 999d) – (b + 999d)
= a – b = 100 ((1) నుండి)
∴ 1000వ పదాల మధ్య తేడా 100.

ప్రశ్న 11.
7 చే భాగించబడే మూడంకెల సంఖ్యలు ఎన్ని కలవు?
సాధన.
మొదటి పద్దతి’:
7 చే భాగింపబడే మూడంకెల సంఖ్యల జాబితా 105, 112, 119, 126, …………., 994 ఈ జాబితా అంకశ్రేణి అవుతుంది.
a = 105; d = a₂ – a₁ = 112 – 105 = 7;
a_n = 994
∴ a_n = a + (n – 1) d = 994
= 105 + (n – 1) 7 = 994
105 + 7n – 7 = 994
7n + 98 = 994
7n = 994 – 98 = 896
n = \(\frac{896}{7}\) = 128
∴ 7 చే భాగింపబడే మూడంకెల సంఖ్యలు 128 కలవు.

రెండవ పద్దతి :
d = \(\frac{a_{n}-a_{m}}{n-m}\)
a₁ = 105, a_n = 994, d = 7, m = 1
7 = \(\frac{994-105}{n-1}=\frac{896}{n-1}\)
n – 1 = \(\frac{889}{7}\) = 127
∴ n = 127 +1 = 128.

ప్రశ్న 12.
10 మరియు 250 ల మధ్య గల 4 యొక్క గుణిజాల సంఖ్యను కనుగొనుము.
సాధన.
10 మరియు 250 ల మధ్య గల 4 యొక్క గుణిజాల జాబితా 12, 16, 20, ……… 248.
ఈ జాబితా A.P లో కలదు.
∴ a = 12, d = a₂ – a₁ = 16 – 12 = 4,
a_n = 248
a_n = a + (n – 1) d = 248 .
= 12 + (n- 1) 4 = 248
= 12 + 4n – 4 = 248
4n = 248 – 8 = 240
n = \(\frac{240}{4}\) = 60
∴ 10 మరియు 250 ల మధ్యగల 4 యొక్క గుణిజాల సంఖ్య = 60.

ప్రశ్న 13.
63, 65, 67, …. మరియు 3, 10, 17, ….. అంకశ్రేఢుల nవ పదాలు సమానము అయిన n విలువను కనుగొనుము.
సాధన.
మొదటి A.P = 63, 65, 67, ……………..
a = 63, d = a₂ – a₁ = 65 – 63 = 2
∴ nవ పదం a_n = a + (n-1) d
= 63 + (n – 1) 2
= 63 + 2n – 2
nవ పదం a_n = 2n + 61 ………….. (1)
రెండవ A.P. = 3, 10, 17, ……………….
a = 3, d = a₂ – a₁ = 10 – 3 = 7
nవ పదం a_n = 3 + (n -1 ) 7
= 3 + 7n – 7
nవ పదం a_n = 7n – 4 ………… (2)
కాని లెక్క ప్రకారం రెండు అంకశ్రేఢుల పదాలు సమానము.
∴ 7n – 4 = 2n + 61
7n – 2n = 61 + 4
5n = 65
n = \(\frac{65}{5}\) = 13
∴ n = 13.

ప్రశ్న 14.
3వ పదము 167; 7వ పదము, 5వ పదము కంటే 12 ఎక్కువగా గల ఒక అంకశ్రేఢిని కనుగొనుము.
సాధన.
A.P లో 3వ పదం a₃ = a + 2d = 16 ….. (1)
5వ పదం a₅ = a + 4d
7వ పదం a₇ = a + 6d
లెక్క ప్రకారం 7వ పదము, 5వ పదము కంటే 12 ఎక్కువ.
a + 6d = (a + 4d) + 12
a + 6d – a – 4d = 12
2d = 12 ⇒ d = \(\frac{12}{2}\) = 6
d = 6 ను (1) లో ప్రతిక్షేపించగా,
a + 2(6) = 16
a + 12 = 16
a = 16 – 12 = 4
a = 4 మరియు d = 6
∴ అంకశ్రేణి 4, 10, 16, 22, …………….

ప్రశ్న 15.
3, 8, 13, ….., 253 అంకశ్రేణి యొక్క చివరి నుంచి 20వ పదమును కనుగొనుము.
సాధన.
మొదటి పద్దతి :
ఇచ్చిన A.P = 3, 8, 13, ………., 253
ఇక్కడ a = 3, d = a₂ – a₁ = 8 – 3 = 5,
⇒a_n = 253
⇒ a_n = a + (n – 1) 4 = 253.
⇒ 3 + (n- 1) 5 = 253
⇒ 3 + 5n – 5 = 253
⇒ 5n = 253 + 2 = 255
⇒ n = \(\frac{255}{5}\) = 51
ఇచ్చిన A.P లో 51 పదాలు కలవు.
∴ చివరి నుండి 20వ పదం, మొదటి నుండి (51 – 20) + 1 = 32వ పదం అవుతుంది.
∴ 32వ పదం a₃₂ = 3 + (32 – 1) (5)
= 3 + 31 (5)
a₃₂ = 3 + 155 = 158
చివరి నుండి 20వ పదం = 158

2వ పద్దతి :
ఇచ్చిన A.P = 3, 8, 13, ….., 253
ఇక్కడ d = a₂ – a₁ = 8 – 3 = 5
ఇచ్చిన శ్రేణిని త్రిప్పి రాయగా వచ్చే 20వ పదమే ఇచ్చిన శ్రేఢి యొక్క చివరి నుండి 20వ పదం అవుతుంది. 253, 248, 243, ………., 13, 8, 3
ఈ శ్రేణిలో a = 253, d = a₂ – a₁
= 248 – 253 = – 5
a_n = 3
a_n = a + (n – 1) d = 3
253 + (n – 1) (- 5) = 3
253 – 5n + 5 = 3
258 – 5n = 3
– 5n = 3 – 258 = – 255
5n = 255
⇒ n = \(\frac{255}{5}\) = 51
∴ 20వ పదం a₂₀ = 253 + (20 – 1) (- 5)
= 253 – 95
a_n = 158
∴ 3, 8, 13, …………. 253 అంకశ్రేఢి యొక్క చివరి నుండి 20వ పదము = 158.

ప్రశ్న 16.
ఒక అంకశ్రేణిలో 4వ మరియు 8వ పదాల మొత్తము 24 మరియు 6వ, 10వ పదాల మొత్తము 44 అయిన మొదటి మూడు పదాలను కనుగొనుము.
సాధన.
A.P లో 4వ పదం = a + 3d
8వ పదం = a + 7d
లెక్క ప్రకారం 4వ, 8వ పదాల ,మొత్తం = 24
(a + 3d) + (a + 7d) = 24
= 2a + 10d = 24
2 (a + 5d) = 24
a + 5d = \(\frac{24}{2}\) = 12
∴ a + 5d = 12 ………….. (1)
ఇలాగే, 6వ పదం = a + 5d
10వ పదం = a + 9d
6వ మరియు 10వ పదాల మొత్తం 44
(a + 5d) + (a + 9d) = 44
2a + 140 = 44
2 (a + 7d) = 44
a + 7d = \(\frac{44}{2}\) = 22
a + 7d = 22 ………… (2)
(2) – (1)

d = \(\frac{10}{2}\) = 5
∴ d = 2
d = 5ను (1) లో ప్రతిక్షేపించగా,
a + 5(5) = 12 ⇒ a = 12 – 25 = – 13
∴ కావలసిన అంకశ్రేణిలోని మొదటి మూడు పదాలు
మొదటి పదం a₁ = a = – 13
రెండవ పదం a₂ = – 13 + 5 = – 8
మూడవ పదం a₃ = 3 – 8 + 5 = – 3

ప్రశ్న 17.
సుబ్బారావు 1995వ సం||లో నెలకు ₹ 5000 జీతంతో ఉద్యోగంలో చేరాడు. అతని జీతము సం||మునకు ₹ 200 పెరిగిన అతని జీతము ఏ సం||ములో ₹ 7000 అవుతుంది ?
సాధన.

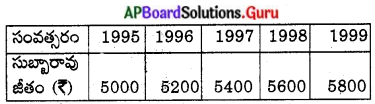
జీతం యొక్క జాబితా
5000, 5200, 5400, 5600, ………….
ఈ జాబితా A.P లో కలదు.
∴ a = 5000, d = a₂ – a₁ = 5200 – 5000 = 200
a_n = 7000
a_n = a + (n – 1) 4 = 7000
= 5000 + (n – 1) 200 = 7000
= 5000 + 200 n – 200 = 7000
200 n = 7000 – 4800 = 2200
∴ n = \(\frac{2200}{200}\) = 11.
జాబితాలో 7000 11వ పదం అవుతుంది.
అనగా ,సుబ్బారావు ఉద్యోగంలో చేరినప్పటి నుండి 11వ సం||లో అతని జీతం ₹ 7000 అవుతుంది. (1995ను కూడా కలుపుకోవాలి)
∴ 2005 వ సం||లో సుబ్బారావు జీతం ₹ 7000 అవుతుంది.