AP Board 10th Class Maths Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.4

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.4 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Exercise 8.4

ప్రశ్న 1.
ఒక రాంబస్ లో భుజాల వర్గాల మొత్తము, దాని కర్ణముల వర్గముల మొత్తమునకు సమానమని చూపండి.
సాధన.

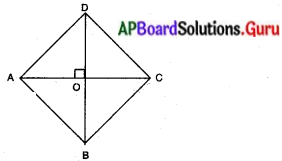
దత్తాంశము : □ABCD ఒక రాంబస్, AC మరియు BD కర్ణాలు ‘0’ వద్ద ఖండించును. రాంబ లో కర్ణాలు పరస్పరం లంబ సమద్విఖండన చేసుకొనును.
సారాంశము : AB² + BC² + CD² + AD² = AC² + BD²
నిరూపణ : ABCD రాంబస్ భుజాల వర్గాల మొత్తం AB² + BC² + CD² + AD²
= AB² + AB² + AB² + AB²
= 4 AB² ……………. (1)
[∵ రాంబస్ లో AB = BC = CD = AD]
∆AOBలో ∠O = 90°
∴ AO² + OB² = AB² (పైథాగరస్ సిద్ధాంతం]
\(\left(\frac{\mathrm{AC}}{2}\right)^{2}\) – (\(\left(\frac{\mathrm{BD}}{2}\right)^{2}\)) = AB²
\(\frac{\mathrm{AC}^{2}}{4}+\frac{\mathrm{BD}^{2}}{4}\) = AB²
AC² + BD² = 4AB² ……………… (2)
(1) మరియు (2) ల నుండి
AB² + BC² + CD² + AD² = AC² + BD²

ప్రశ్న 2.
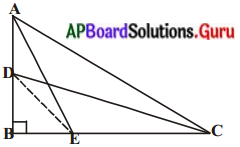
లంబకోణ త్రిభుజము ABCలో లంబకోణము శీర్షము ‘B’ వద్ద కలదు. D మరియు E బిందువులు వరుసగా AB, BC లపై ఏవైనా రెండు బిందువులు. అయిన AE² + CD² = AC² + DE² అని చూపండి.

సాధన.
దత్తాంశము : ∆ABCలో LB = 90°, D మరియు Eలు AB మరియు BC లపై గల బిందువులు.
సారాంశము : AE² + CD² = AC² + DE²
ఉపపత్తి : ∆BCD ఒక లంబకోణ త్రిభుజం. B వద్ద లంబకోణము కావున,
BD² + BC² = CD² ………….. (1) [∵ పైథాగరస్ సిద్ధాంతం నుండి)
∆ABEలో ∠B = 90° కావున AB² + BE² = AE²
(1), (2) లను కూడగా
BD² + BC² + AB² + BE² = CD² + AE²
(BD² + BE²) + (AB² + BC²) = CD² + AE²
DE² + AC² = CD² + AE²
[∵ ADBEలో, LB = 90° కావున DE² = BD² + BE² ∆ ABCలో, ∠B = 90° కావున AC² = AB² + BC²].

ప్రశ్న 3.
ఒక సమబాహు త్రిభుజములో భుజము వర్గమునకు – మూడు రెట్లు, దాని ఉన్నతి (లంబము) వర్గమునకు నాలుగురెట్లు అని చూపండి.
సాధన.
దత్తాంశము : ∆ABC ఒక సమబాహు త్రిభుజములో AD ఉన్నతి. భుజము a యూనిట్లు, ఉన్నతి hయూనిట్లు.
సారాంశము : 3a² = 4h²

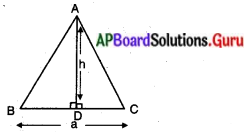
ఉపపత్తి : ∆ABD, ∆ACD లలో
∠B = ∠C [∵ 60°]
∠ADB = ∠ADC [∵ 90°]
∴ ∠BAD = ∠DAC
[∵ త్రిభుజ కోణాల మొత్తం ధర్మము] మరియు BA = CA
∴ ∆ABD ≅ ∆ACD (భు. కో. భు సరూపకత నియమం నుండి)
BD = CD = \(\frac{1}{2}\) BC = \(\frac{a}{2}\)
∆ABD, AB² = AB² + BD² [∵ పైథాగరస్ సిద్ధాంతం నుండి]
a² = h² + (\(\frac{a}{2}\))²
a² = h²
h² = \(\frac{4 a^{2}-a^{2}}{4}\)
∴ h² = \(\frac{3 a^{2}}{4}\) = 3a² = 4h²

ప్రశ్న 4.
POR త్రిభుజంలో లంబకోణము శీర్షము ‘P’ వద్ద కలదు. PM ⊥ QR అగునట్లు QR పై బిందువు M అయిన PM² = OM . MR అని చూపండి.
సాధన.

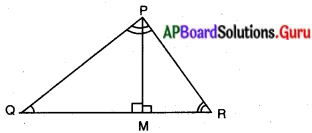
దత్తాంశము : ∆PORలో, ∠P = 90° మరియు PM ⊥ QR.
సారాంశము : PM² = QM. MR.
ఉపపత్తి : ∆POR; ∆MPR లలో ∠P = ∠M [ప్రతికోణం 90°]
∠R = ∠R (ఉమ్మడి కోణం]
∴ ∆PQR ~ ∆MPR ………. (1) [కో.కో. సరూపకత]
∆PQR మరియు ∆MQP లలో ∠P = ∠M (ప్రతికోణం 90°).
∠Q = ∠Q (ఉమ్మడికోణం)
∴ ∆PQR ~ ∆MQP ………….. (2)
(కో.కో. సరూపకత) (1), (2) ల నుండి
∆PQR ~ ∆MPR ~ ∆MQP (పరావర్తన ధర్మము]
∴ ∆MPR ~ ∆MQP (సరూప త్రిభుజాల అనురూప భుజాల నిష్పత్తులు సమానము]
\(\frac{\mathrm{PM}}{\mathrm{QM}}=\frac{\mathrm{MR}}{\mathrm{PM}}\)
PM . PM = MR. AM
PM² = OM . MR.

ప్రశ్న 5.
త్రిభుజము ABD లో లంబకోణము A వద్ద కలదు. మరియు AC ⊥ BD అయిన
(i) AB² = BC . BD
(ii) AC = BC . DC
(iii) AD = BD. CD అని చూపండి.

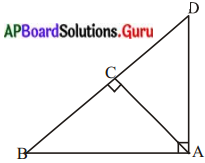
సాధన.
దత్తాంశము : ∆ABD లో ∠A వద్ద లంబకోణము కలదు. మరియు AC ⊥ BD.
సారాంశము :
(i) AB² = BC . BD
(ii) AC² = BC. DC
(iii) AD² = BD. CD
ఉపపత్తి :
(i) ∆ABD మరియు ∆CAB లలో
∠BAD = ∠ACB [ప్రతికోణం 90°].
∠B = ∠B [ఉమ్మడి కోణము]
∴ ∆ABD ~ ∆CAB (కో.కో. సరూపకత నియమం నుండి)
\(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BC}}{\mathrm{AB}}\) (సరూప త్రిభుజాల అనురూప భుజాల నిష్పత్తులు సమానం)
⇒ \(\frac{\mathrm{AB}}{\mathrm{BD}}=\frac{\mathrm{BC}}{\mathrm{AB}}\)
∴ AB² = BC. BD.

(ii) ∆ABD మరియు ∆CAD లలో
∠BAD = ∠ACD (ప్రతికోణము 909)
∠D = ∠D (ఉమ్మడి కోణము)
∴ ∆ABD ~ ∆CAD (క్రో.కో.కో సరూపకత)
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{AD}}=\frac{\mathrm{AD}}{\mathrm{CD}}\)
⇒ \(\frac{\mathrm{BD}}{\mathrm{A} \cdot \mathrm{D}}=\frac{\mathrm{AD}}{\mathrm{CD}}\)
∴ AD² = BD . CD.

(iii) (i) మరియు (ii) ల నుండి,
∆ACB ~ ∆DCA [∵ ∆BAD ~ ∆BCA ~ ∆ACD)
\(\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{BC}}{\mathrm{AC}}\)
\(\frac{\mathrm{AC}}{\mathrm{DC}}=\frac{\mathrm{BC}}{\mathrm{AC}}\)
∴ AC² = BC . DC.

ప్రశ్న 6.
సమద్విబాహు త్రిభుజము ABCలో లంబకోణము C వద్ద కలదు. అయిన AB² = 2AC² అని చూపండి.
సాధన.

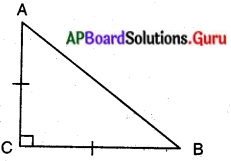
దత్తాంశము : ∆ABCలో ∠C = 90° మరియు AC = BC.
సారాంశము : AB² = 2AC²
ఉపపత్తి : ∆ACBలో ∠C = 90° కావున AC² + BC² = AB² [పైథాగరస్ నియమం నుండి)
⇒ AC = BC (దత్తాంశము)
AB² = 2AC².

ప్రశ్న 7.
త్రిభుజము ABC అంతరంలో ఏదైనా బిందువు ‘0’. OD ⊥ BC, OE ⊥ AC మరియు OF ⊥ AB అయిన
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF² అని చూపండి.

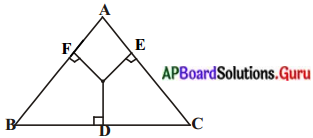
సాధన.
దత్తాంశము : ∆ABCలో ‘O’ అంతర బిందువు OD ⊥ BC, OE ⊥ AC మరియు OF ⊥ AB.
సారాంశము :
(i) OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²
(ii) AF² + BD² + CE² = AE² + CD² + BF²
ఉపపత్తి :
(i) ∆OAFలో OA² = AF² + OF² (పైథాగరస్ సిద్ధాంతం నుండి]
⇒ OA² – OF² = AF² ………….. (1)
∆OBD లో
OB² = BD² + OD²
⇒ OB² – OD² = BD² ………… (2)
∆OCE లో
OC² = CE+ + OE
OC² – OE² = CE² ………….. (3)
(1), (2) మరియు (3) లను కూడగా
OA² – OF² + OB² – OD² + OC² – OE² = AF² + BD² + CE²
∴ OA² + OB² + OC² – OD² – OE² – OF² = AF² + BD² + CE²

(ii) ∆OAE లో OA² = AE² + OE² …….. (1)
⇒ OA² – OE² = AE²
∆OBF లో
OB² = BF² + OF²
OB² – OF² = BF² ……… (2)
∆OCD లో
OC² = OD² + CD²
OC² – OD² = CD² …………. (3)
(1), (2) మరియు (3) లను కూడగా
OA² – OE² + OB² – OF² + OC² – OD² = AE² + BF² + CD²
OA² + OB² + OC² – OD² – OE² – OF² = AE² + CD² + BF²
∴ AF² + BD² + CE² = AE² + CD² + BF². [సమస్య (i) నుండి].

ప్రశ్న 8.
18 మీటర్ల పొడవు గల ఒక నిలువు స్తంభానికి 24 మీటర్ల పొడవు గల ఒక తీగ కట్టబడినది. తీగ రెండవ చివరకు ఒక మేకు కట్టబడినది. భూమిపై స్తంభం నుండి ఎంత దూరములో ఆ మేకును పాతిన ఆ తీగ బిగుతుగా నుండును ?
సాధన.

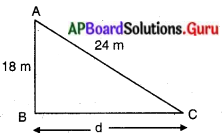
AB = స్తంభం ఎత్తు = 18మీ
AC = తీగ పొడవు = 24 మీ.
స్తంభం నుండి మేకుకు గల దూరము = dమీ
పైథాగరస్ సిద్ధాంతం నుండి AC² = AB² + BC²
24² = 18² + d²
d² = 24² – 18²
= 576 – 324 = 252
= √(36 × 7)
∴ d = 6√7 మీ.

ప్రశ్న 9.
6మీ. మరియు 11మీటర్ల పొడవు గల రెండు స్తంభాలు ఒక చదునైన నేలపై ఉన్నాయి. ఆ రెండు స్తంభాల అడుగు భాగముల మధ్య దూరము 12మీ. అయిన ఆ రెండు స్తంభాల పై కొనల మధ్యదూరము ఎంత ?
సాధన.

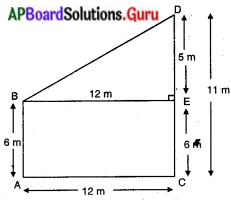
మొదటి స్తంభం ఎత్తు = AB = 6 మీ. అనుకొనుము
రెండవ స్తంభం ఎత్తు = CD = 11 మీ. అనుకొనుము
స్తంభాల మధ్య దూరము = AC = 12 మీ.
పటం నుండి □ACEB ఒక దీర్ఘ చతురస్రము.
∴ AB = CE = 6 మీ.
ED = CD – CE = 11 – 6 = 5 మీ.
∆BEDలో ∠E = 90°; DE = 5 మీ, BE = 12 మీ.
∴ BD² = BE² + DE²
= 12² + 5² = 144 + 25
BD² = 169
∴ BD = √169 = 13 మీ.
∴ స్తంభాల కొనల మధ్య దూరము = 13 మీ.

ప్రశ్న 10.
సమబాహు త్రిభుజము ABCలో, భుజం BC పై . బిందువు ‘D’, ఇంకా BD = \(\frac{1}{3}\) BC అయిన 9AD² = 7AB² అని చూపండి.
సాధన.

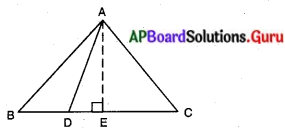
దత్తాంశము : ∆ABC ఒక సమబాహు త్రిభుజము. భుజం BC పై ‘D’ ఒక బిందువు మరియు BD = \(\frac{1}{3}\) BC.
సారాంశం : 9 AD² = 7AB²
నిర్మాణము : BC పైకి A నుండి మధ్యగతమును తీయగా అది E వద్ద ఖండించును.
ఉపపత్తి : ∆AEDలో; ∠D = 90° [∵ సమబాహు త్రిభుజంలో ఉన్నతి. మరియు మధ్యగతాలు సమానములు]
∴ AD² = AE² + DE² ………… (1) [∵ పైథాగరస్ సిద్ధాంతం నుండి]
∆AECలో; AC² = AE² + CE²
AE² = AC² – CE² (పైథాగరస్ సిద్ధాంతం నుండి)
AE² = AC² – CE²
[∵ AB = AC; CE = \(\frac{1}{2}\) BC]
[∵ AB = AC; CE = \(\frac{1}{2}\) BC = \(\frac{1}{2}\) AB
∵ BC = AB = AC దత్తాంశం)
= AB² – (\(\frac{1}{2}\) AB)²
= AB² – \(\frac{1}{4}\) AB² = \(\frac{3}{4}\) AB² ……. (2)
పటం నుండి,
DE = BE – BD = \(\frac{1}{2}\) BC – \(\frac{1}{3}\) BC
[BC మధ్య బిందువు E కావున BE = \(\frac{1}{2}\) BC; BD = \(\frac{1}{3}\) BC]
= \(\frac{1}{6}\) BC
= \(\frac{1}{6}\) AB
∴ DE = \(\frac{1}{36}\) AB²
AD² = \(\frac{3}{4}\) AB² + \(\frac{1}{36}\) AB²
= \(\left(\frac{27+1}{36}\right)\) AB²
AD² = \(\frac{28}{36}\) AB²
⇒ AD² = \(\frac{7}{9}\) AB²
⇒ 9 AD² = 7 AB²

ప్రశ్న 11.
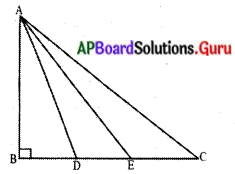
ఇచ్చిన పటంలో, ∆ABC ఒక లంబకోణ త్రిభుజము. శీర్షము B వద్ద లంబకోణము కలదు. BC భుజాన్ని Dమరియు E బిందువులు సమత్రిఖండన చేస్తే అయిన BA² = 3AC² + 5AD² అని చూపండి. –

సాధన.
దత్తాంశము : ∆ABCలో 2B = 90° మరియు D, E లు సమత్రిఖండన బిందువులు.
సారాంశము : 8AE² = 3AC² + 5AD²
ఉపపత్తి : ∆ABCలో ∠B = 90° మరియు AC² = AB² + BC² [పైథాగరస్ నియమం నుండి]
3AC² = 3 (AB² + BC²) [ఇరువైపుల ‘3’ చే గుణించగా]
3AC² = 3AB² + 3BC²
= 3 AB² + 3[\(\frac{3}{2}\) BE²]
[∵ BE = \(\frac{2}{3}\) BC; D, E లు సమత్రిఖండన బిందువులు. ]
3AC² = 3AB² + \(\frac{27}{4}\) BE² ……………… ( 1 )
∆ABDలో ∠B = 90°
∴ AD² = AB² + BD²
5AD² = 5[AB² + BD²] [ఇరువైపుల ‘5’ చే గుణించగా]
= 5 AB² + 5 BD²
= 5 AB² + 5[\(\frac{1}{2}\)BE]²
[∵ BC యొక్క సమత్రిఖండన బిందువులు D మరియు E లు BD = DE]
5AD² = 5AB² + A BE² ……………… (2)
(1), (2) లను కూడగా
3AC² + 5AD² = 3AB² + \(\frac{27}{4}\) BE² + 5AB² + \(\frac{5}{4}\) BE²
= 8AB² + (\(\frac{27+5}{4}\)) BE²
= 8AB² + \(\frac{32}{4}\) BE²
= 8(AB² + BE²)
3AC² + 5AD² = 8AE².
[∵ ∆ABEలో AB² + BE² = AE² పైథాగరస్ సిద్ధాంతం నుండి].

 

ప్రశ్న 12.
సమద్విబాహు త్రిభుజము ABCలో, లంబకోణము ‘B’ వద్ద కలదు. AC మరియు AB భుజాలపై సరూప త్రిభుజాలు ACD మరియు ABE నిర్మింపబడినవి. అయిన ∆ABE మరియు ∆ACDల వైశాల్యాల నిష్పత్తిని కనుగొనండి.

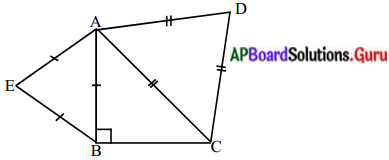
సాధన.
దత్తాంశం : ∆ABCలలో, AB = BC మరియు ∠B = 90°. AC మరియు AB భుజాలపై సరూప త్రిభుజాలు ACD మరియు ABE లు.
∆ABC లంబకోణ సమద్విబాహు త్రిభుజపు సమాన భుజాలు AB = BC = a అనుకొనుము.
∆ABCలో, ∠B = 90°, AC² = AB² + BC²
= a² + a² = 2a²
కావున ∆ABE ~ ∆ACD
\(\frac{\Delta \mathrm{ABE}}{\Delta \mathrm{ACD}}=\frac{\mathrm{AB}^{2}}{\mathrm{AC}^{2}}\)
[సరూప త్రిభుజ వైశాల్యాలు వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము] .
= \(\frac{a^{2}}{2 a^{2}}=\frac{1}{2}\)
∴ ∆ABE : ∆ACD = 1 : 2.