AP Board 10th Class Maths Solutions Chapter 8 సరూప త్రిభుజాలు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
క్రింది ఖాళీలను సరూపాలు సరూపాలు కావుచే పూరించండి. (పేజీ నెం. 194)
(i) అన్ని చతురస్రాలు ఎల్లప్పుడూ ……………………
సాధన.
సరూపాలు

(ii) అన్ని సమబాహు త్రిభుజాలు ఎల్లప్పుడూ ……………………
సాధన.
సరూపాలు

(iii) అన్ని సమద్విబాహు త్రిభుజాలు ……………………
సాధన.
సరూపాలు కావు.

(iv) సమాన సంఖ్యలో భుజాలు కలిగిన రెండు బహు భుజు లో అనురూపకోణాలు సమానము మరియు అనురూ పభుజులు సమానము అయిన అవి ……………………
సాధన.
సరూపాలు

(v) పరిమాణము తగ్గించబడిన లేదా పెంచబడిన ఒక వస్తువు యొక్క ఫోటోగ్రాు ……………………
సాధన.
సరూపాలు

(vi) రాంబస్ మరియు చతురస్రాలు ఒకదానికొకటి ……………….
సాధన.
సరూపాలు కావు.

ప్రశ్న 2.
క్రింది ప్రవచనాలు సత్యమో, అసత్యమో రాయండి. (పేజీ నెం. 194)
(i) రెండు సరూపపటాలు సర్వసమానాలు
సాధన.
అసత్యము

(ii) రెండు సర్వసమాన పటాలు సరూపాలు
సాధన.
సత్యము

(iii) రెండు బహుభుజులకు అనురూపకోణాలు సమానాలైన అవి సరూపాలు.
సాధన.
అసత్యము

ప్రశ్న 3.
ఈ క్రింది వాటికి రెండు వేరువేరు ఉదాహరణలివ్వండి. (i) సరూప పటాలు, (ii) సరూప పటాలు కానివి (పేజీ నెం. 194)
(i) సరూప పటాలు
సాధన.
(a) ఏవైనా రెండు వృత్తాలు
(b) ఏవైనా రెండు చతురస్రాలు
(c) ఏవైనా రెండు సమబాహు త్రిభుజాలు

(ii) సరూప పటాలు కానివి
సాధన.
(a) ఒక చతురస్రము మరియు ఒక రాంబస్
(b) ఒక చతురస్రము మరియు ఒక దీర్ఘచతురస్రము.

ప్రశ్న 4.
ఇచ్చిన పటంలో X యొక్క ఏ విలువ (లు)కు DE || AB అగును ? (పేజీ నెం. 200) AD = 8x + 9, CD = x + 3, BE = 3x + 4, CE = x.

సాధన.
దత్తాంశము : ∆ABC, DE || AB AD = 8x + 9, CD = x + 3, BE = 3x + 4 మరియు CE = x
ప్రాథమిక సిద్ధాంతమును అనుసరించి DE || AB
అయిన \(\frac{\mathrm{CD}}{\mathrm{DA}}=\frac{\mathrm{CE}}{\mathrm{EB}}\) అగును.
⇒ \(\frac{x+3}{8 x+9}=\frac{x}{3 x+4}\)
(x + 3) (3x + 4) = x {8x + 9) (అడ్డ గుణకారము చేయగా),
⇒ x (3x + 4) + 3 (3x + 4) = 8x² + 9x
⇒ 3x² + 4x + 9x + 12 = 8x² + 9x
⇒ 8x² + 9x – 3x² – 13x – 12 = 0
⇒ 5x² – 4x – 12 = 0
⇒ 5x² – 10x + 6x – 12 = 0
⇒ 5x (x – 2) + 6 (x – 2) = 0
⇒ (5x + 6) (x – 2) = 0
⇒ 5x + 6 = 0 లేక X – 2 = 0
⇒ x = \(\frac{-6}{5}\) లేక x = 2 విలువలకు DE || AB అగును.

ప్రశ్న 5.
∆ABC లో DE || BC. AD = x, DB = x = 2, AE = x + 2 మరియు EC = x – 1. అయిన x విలువను కనుగొనుము. (పేజీ నెం. 200)
సాధన.
దత్తాంశము : ∆ABC లో, DE || BC
ప్రాథమిక సిద్ధాంతము నుండి \(\frac{A D}{D B}=\frac{A E}{E C}\)
⇒ \(\frac{x}{x-2}=\frac{x+2}{x-1}\)
⇒ x (x – 1) = (x + 2) (x – 2)
⇒ x² – x = x² – 4
⇒ – x = – 4
∴ x = 4.

ప్రయత్నించండి :

ప్రశ్న 1.
∆PQRలో భుజాలు PQ మరియు PR లపై బిందువులు వరుసగా E మరియు F. ఈ క్రింది వాటిలో ప్రతి సందర్భంలో EF ||QR అవునో, కాదో తెల్పండి. (పేజీ నెం. 197)
(i) PE = 3.9 సెం.మీ, EQ = 3 సెం.మీ, PF = 3.6 సెం.మీ, FR = 2.4 సెం.మీ.
సాధన.

ఇక్కడ, \(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{3.9}{3}=\frac{1.3}{1}\)

\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{2.4}=\frac{0.3}{0.2}\) \(\frac{P E}{E Q} \neq \frac{P F}{F R}\)

కావున, EF // QR కాదు.

(ii) PE = 4 సెం.మీ, QE = 4.5 సెం.మీ, PF = 8 సెం.మీ, RF = 9 సెం.మీ.
సాధన.
ఇక్కడ, \(\frac{P E}{E Q}=\frac{4}{4.5}=\frac{0.8}{0.9}=\frac{8}{9}\)

\(\frac{\mathrm{PF}}{\mathrm{RF}}=\frac{8}{9}\)

\(\frac{P E}{E Q}=\frac{P F}{R F}\) కావున
∴ EF || QR అగును.

(ii) PQ = 1.28 సెం.మీ, PR = 2.56 సెం.మీ, PE = 1.8 సెం.మీ, PF = 3.6 సెం.మీ.
సాధన.

దత్తాంశము : PQ = 1.28 సెం.మీ.
PE = 1:8 సెం.మీ.
⇒ EQ = PE – PQ = 1.8 – 1.28
⇒ EQ = 0.52 సెం.మీ. మరియు
PR = 2.56 సెం.మీ.
PF = 3.6 సెం.మీ.
FR = PF – PR = 3.6 – 2.56 = 1.04 సెం.మీ.
ఇప్పుడు \(\frac{P E}{E Q}=\frac{1.8}{0.52}=\frac{0.9}{0.26}\)
\(\frac{\mathrm{PF}}{\mathrm{FR}}=\frac{3.6}{1.04}=\frac{0.9}{0.26}\)
\(\frac{\mathrm{PE}}{\mathrm{EQ}}=\frac{\mathrm{PF}}{\mathrm{FR}}\)
∴ EF || QR (ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము నుండి)

ప్రశ్న 2.
ఈ క్రింది పటాలలో DE || BC (పేజీ నెం. 198)
(i) ECని కనుగొనుము.

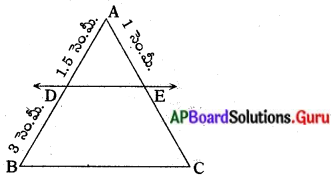
సాధన.
పటం నుండి \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{1.5}{3}=\frac{1}{E C}\)
∴ EC = \(\frac{1.5}{3}\) = 2 సెం.మీ.

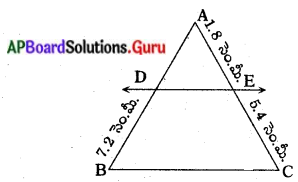
(ii) AD ని కనుగొనుము.

సాధన.
పటం నుండి \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
⇒ \(\frac{\mathrm{AD}}{7.2}=\frac{1.8}{5.4}\)
∴ AD = \(\frac{1.8 \times 7.2}{5.4}\) = 2.4 సెం.మీ.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
నిజ జీవితంలో ఇలా ‘స్కేలు’ను ఉపయోగించే సందర్భాలకు మరికొన్ని ఉదాహరణలు చెప్పగలరా ? (పేజీ నెం. 192)
సాధన.
స్కేలు గుణకంను మ్యాపుల తయారీలో, యంత్రాల తయారీ విభాగాలలో ఉపయోగిస్తారు.

ప్రశ్న 2.
ఒక చతురస్రము, రాంబస్ సరూపాలని నీవు చెప్పగలవా? నీ మిత్రులతో చర్చించుము. ఆ నియమాలు ఎందుకు సరిపోతాయో లేదా ఎందుకు సరిపోవో కారణాలు వ్రాయుము. (పేజీ నెం. 193)
సాధన.
చతురస్రము మరియు రాంబస్ సరూపాలు కావు.
వాని, అనురూప భుజాల నిష్పత్తులు సమానం, కాని వాని అనురూప కోణములు సమానం కాదు. కావున ఇవి సరూపాలు కావు. –

\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{CD}}{\mathrm{RS}}=\frac{\mathrm{AD}}{\mathrm{PS}}\)

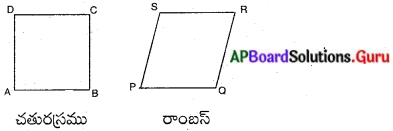
∠A ≠ ∠P; ∠B ≠ ∠Q;
∠C ≠ ∠R; ∠D ≠ ∠S.

సిద్ధాంతములు:

ప్రశ్న 1.
ప్రాథమిక అనుపాత సిద్ధాంతము (థేల్స్ సిద్ధాంతము): ‘ఒక త్రిభుజంలో ఒక భుజానికి సమాంతరంగా గీసిన రేఖ మిగిలిన రెండు భుజాలను వేరువేరు బిందువులలో ఖండించిన, ఆ మిగిలిన రెండు భుజాలు ఒకే నిష్పత్తిలో విభజింపబడతాయి. (పేజీ నెం. 195)
సాధన.
దత్తాంశము : ∆ABC లో DE || BC, DE రేఖ AB, AC భుజాలను వరుసగా D మరియు E.వద్ద ఖండించును.
సారాంశము : \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
నిర్మాణము : B, E మరియు C, D లను కలుపుము మరియు DM ⊥ AC, EN ⊥ AB లను గీయుము.
ఉపపత్తి : ∆ADE వైశాల్యము = \(\frac{1}{2}\) × AD × EN
∆BDE వైశాల్యము = \(\frac{1}{2}\) × BD × EN

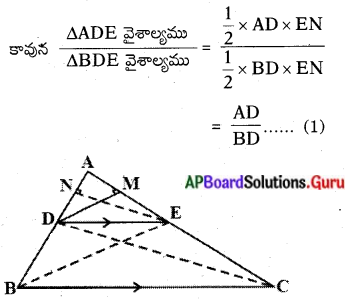
మరల ∆ADE వైశాల్యము = \(\frac{1}{2}\) × AE × DM
∆CDE వైశాల్యము = \(\frac{1}{2}\) × EC × DM

∆BDE, ∆CDE లు ఒకే భూమి DE మరియు సమాంతర రేఖలు BC .మరియు DE ల మధ్య ఉన్నట్లు గమనించవచ్చును.
కావున ∆BDE వైశాల్యము = ∆CDE వైశాల్యము …… (3)
(1), (2), (3) ల నుండి
\(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\)
కావున సిద్ధాంతము నిరూపించబడినది.

ప్రశ్న 2.
ప్రాథమిక సిద్ధాంతమునకు విపర్యయము : ఒక త్రిభుజములో ఏవైనా రెండు భుజాలను ఒకే నిష్పత్తిలో విభజించు సరళరేఖ, మూడవ భుజానికి సమాంతరంగా ఉండును. (పేజీ నెం. 197)
సాధన.
దత్తాంశము : ∆ABC లో, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) అగునటు గీయబడిన సరళరేఖ DE
సారాంశము : DE || BC

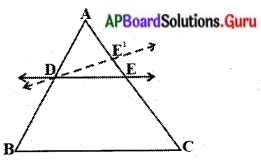
ఉపపత్తి : DE, BCకి సమాంతరము కాదు అనుకొనుము. అపుడు BC కి సమాంతరంగా DE ను గీయుము.
అపుడు \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}^{1}}{\mathrm{E}^{1} \mathrm{C}}\) (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
∴ \(\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{\mathrm{AE}^{1}}{\mathrm{E}^{1} \mathrm{C}}\) (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
ఇరువైపులా ‘1’ కలుపగా, E మరియు E’లు తప్పనిసరిగా ఏకీభవించాలి అని తెలుస్తుంది.

= EC = E’C

ప్రాథమిక సిద్ధాంతం నుండి AE = EC మరియు AE’ = E’C అగును.
ఇది అసంభవం. కనుక E మరియు E’ లు ఏకీభవించును. కనుక DE’ అనునది రేఖయే.
∴ DE||BC అగును. సిద్ధాంతం నిరూపించబడినది.

ప్రయత్నించండి:

ప్రశ్న 1.
క్రింది త్రిభుజాలు సరూపాలా ? సరూపాలయితే ఏ నియమం ఆధారంగానో వివరించండి. త్రిభుజాల సరూపకతను గుర్తులనుపయోగించి రాయండి. (పేజీ నెం. 207)

(i)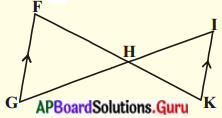

సాధన.
పటంలో ∠G = ∠I మరియు ∠F= ∠K (ఏకాంతర కోణాలు) ∠FHG = ∠IHK (శీర్షాభిముఖ కోణాలు) కో.కో.కో. నియమం ప్రకారము ∆GFH ~ ∆IKH.

(ii)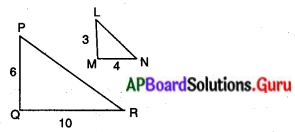

సాధన.
\(\frac{\mathrm{PQ}}{\mathrm{QR}}=\frac{6}{10}=\frac{3}{5}\);

\(\frac{\mathrm{LM}}{\mathrm{MN}}=\frac{3}{4}\)

\(\frac{\mathrm{PQ}}{\mathrm{QR}} \neq \frac{\mathrm{LM}}{\mathrm{MN}}\)
∴ ∆POR మరియు ∆LMN లు సరూపాలు కావు.

(iii)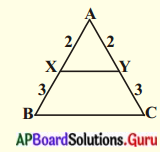

సాధన.
∠A = ∠A (ఉమ్మడి కోణం )
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{5}{5}\) = 1;

\(\frac{\mathrm{AX}}{\mathrm{AY}}=\frac{2}{2}\) = 1

⇒ \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AX}}{\mathrm{AY}}\)
∴ ∆ABC మరియు ∆AXYలు భు.కో.భు. సరూపకత నియమం ప్రకారం సరూపకాలు.
∴ ∆ABC ~ ∆AXY.

(iv)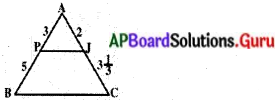

సాధన.
∠A = ∠A (ఉమ్మడి కోణం)
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{8}{5 \frac{1}{3}}=\frac{8}{\frac{16}{3}}=8 \times \frac{3}{16}=\frac{3}{2}\)

\(\frac{\mathrm{AP}}{\mathrm{AJ}}=\frac{3}{2}\);

\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{AP}}{\mathrm{AJ}}\) భు.కో. భు సరూపకత నియమం నుండి ∆ABC ~ ∆APJ
∴ ∆ABC మరియు ∆APJ లు సరూపాలు.

(v)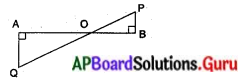

సాధన.
∠A = ∠A = 90°
∠AOQ = ∠POB (శీర్షాభిముఖ కోణాలు)
∠Q = ∠P (ఏకాంతర కోణాలు)
∴ ∆AOQ మరియు ∆BOPలు కో.కో..కో సరూపకత నియమము ప్రకారము సరూపాలు.
∆AOQ ~ ∆BOP.

(vi)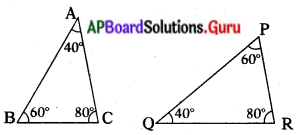

సాధన.
∠A = ∠Q
∠B = ∠P
∠C = ∠R
∆ABC మరియు ∆QPR లు కో.కో.కో సరూపకత నియమం ప్రకారం సరూపకాలు. ∆ABC ~ ∆QPR.

(vii)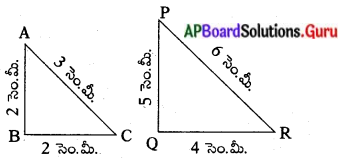

సాధన.

∴ ∆ABC మరియు ∆PORలు సరూపకాలు కావు.

(viii)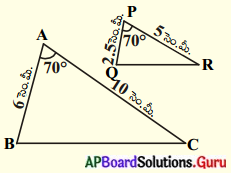

సాధన.
∠A = ∠P (దత్తాంశము)
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{6}{10}=\frac{3}{5}\);

\(\frac{\mathrm{PQ}}{\mathrm{PR}}=\frac{2.5}{5}=\frac{1}{2}\)

\(\frac{\mathrm{AB}}{\mathrm{AC}} \neq \frac{\mathrm{PQ}}{\mathrm{PR}}\)
∴ ∆ABC మరియు ∆PQRలు సరూపకాలు కావు.

ప్రశ్న 2.
ఈ క్రింది త్రిభుజాలు ఎందుకు సరూపాలో వివరించి అపుడు ‘x’ విలువను కనుగొనండి. (పేజీ నెం. 207)

(i)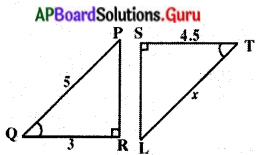

సాధన.
దత్తాంశము : ∆PQR మరియు ∆LTS లలో ∠Q = ∠T, ∠R = ∠S
కో.కో. సరూపకత నియమము ప్రకారము
∆PQR ~ ∆LTS
కావున \(\frac{\mathrm{PQ}}{\mathrm{QR}}=\frac{\mathrm{LT}}{\mathrm{TS}}\)

∴ \(\frac{5}{3}=\frac{x}{4.5}\)
⇒ x = \(\frac{5 \times 4.5}{3}\) = 5 × 1.5 = 7.5

(ii)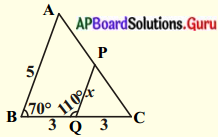

సాధన.
దత్తాంశము : ∆ABC మరియు ∆PQC లలో
∠B = ∠Q [∵ ∠PQC = 180° – 110° = 70° రేఖీయ ద్వయము]
∠C = ∠C [∵ ఉమ్మడి కోణాలు]
(క్రో.కో. సరూపకత నియమం ప్రకారం)
∴ ∆ABC ~ ∆PQC వాటి అనురూప భుజాల కొలతల నిష్పత్తి సమానం కావున
\(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{PQ}}{\mathrm{QC}}\)

\(\frac{5}{6}=\frac{x}{3}\)
x = \(\frac{5}{6}\) × 3
⇒ x = \(\frac{5}{2}\) = 2.5

(iii)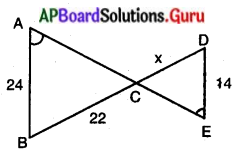

సాధన.
దత్తాంశము : ∆ABC మరియు ∆ECD లలో ∠A = ∠E (దత్తాంశము)
∠ACB = ∠ECD [∵ శీర్షాభిముఖ కోణాలు]
∴ ∆ABC ~ ∆EDC (కో.కో. నియమం ప్రకారం)
కావున, \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{ED}}{\mathrm{DC}}\)
\(\frac{24}{22} \equiv \frac{14}{x}\)
24x = 22 × 14
⇒ x = \(\frac{5 \times 4.5}{3}\) = 7.5

(iv)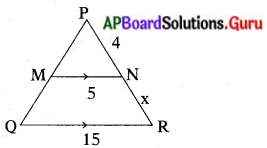

సాధన.
దత్తాంశము : ∆RAB మరియు ∆RST లలో
∠R = ∠R (ఉమ్మడి కోణం ) ∠A = ∠S S08W ∠B = ∠T [AB || ST కావున ఏర్పడిన సదృశ్య కోణాల జత]
∴ ∆RAB ~ ∆RST [∵ కో.కో.కో సరూపకత నియమం]
\(\frac{\mathrm{RA}}{\mathrm{AB}}=\frac{\mathrm{RS}}{\mathrm{ST}}\)
\(\frac{6}{9}=\frac{8}{x}\)
⇒ x = \(\frac{9 \times 8}{6}\) = 12.

(v)

సాధన.
దత్తాంశము : ∆PQR మరియు ∆PMN లలో
∠P = ∠P (ఉమ్మడి కోణము)
∠Q = ∠M [∵ MN || QR కావున ఏర్పడిన సదృశ్య కోణాల జత]
∠R = ∠N
∴ ∆POR ~ ∆PMN [∵ కో.కో.కో సరూపకత నియమం]
\(\frac{\mathrm{PR}}{\mathrm{QR}}=\frac{\mathrm{PN}}{\mathrm{MN}}\)

\(\frac{4+x}{15}=\frac{4}{5}\)
4 + x = \(\frac{4}{5}\) × 15
4 + x = 12
∴ x = 12 – 4 = 8.

(vi)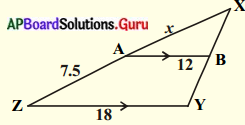

సాధన.
దత్తాంశము : ∆XYZ మరియు ∆XBA లలో
∠X= ∠X [∵ ఉమ్మడి కోణము]
∠B = ∠Y ∠A = ∠Z (∵ AB || ZY కావున ఏర్పడిన సదృశ్య కోణాల జత]
∴ ∆XYZ ~ ∆XBA [∵ కో.కో.కో సరూపకత]
\(\frac{\mathrm{XZ}}{\mathrm{YZ}}=\frac{\mathrm{AX}}{\mathrm{BA}}\)

\(\frac{7.5+x}{18}=\frac{x}{12}\)

7.5 + x = \(\frac{x}{12}\) × 18
2(7.5 + x) = 3x
15 + 2x = 3x
15 = 3x – 2x
⇒ 15 = x .

(vii)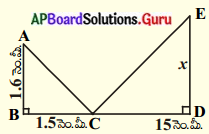

సాధన.
దత్తాంశము :
గమనిక: ∠A = ∠E కో.కో.కో సరూపకత నియమం ప్రకారం ∆ABC ~ ∆EDC అగును.
మరియు \(\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{CD}}=\frac{\mathrm{AC}}{\mathrm{EC}}\)
\(\frac{1.6}{x}=\frac{1.5}{15}\)
x = \(\frac{15 \times 1.6}{1.5}\) = 16

(viii)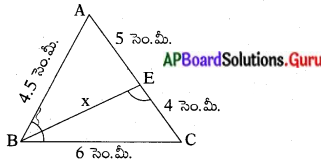

సాధన. ∆ABC మరియు ∆BEC లలో
∠C = ∠C (ఉమ్మడి కోణం)
∠ABC = ∠BEC (దత్తాంశము)
∴ ∆ABC ~ ∆BEC (కో.కో. నియమం)
\(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)

⇒ \(\frac{\mathrm{AB}}{\mathrm{BC}}=\frac{\mathrm{BE}}{\mathrm{EC}}\)

x = \(\frac{4.5}{6}\) × 4 = 3 సెం.మీ.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
త్రిభుజముల సరూపత అనేది మిగిలిన బహుభుజుల సరూపత కంటే ఏ విధంగా భిన్నమైనదో మీ స్నేహితులతో చర్చించండి. (పేజీ నెం. 203)
సాధన.
రెండు త్రిభుజాలలో రెండు అనురూప కోణాలు సమానమైన . ఆ రెండు త్రిభుజాలు . సరూపాలు అవుతాయి. కానీ బహుభుజులలో ఈ నియమము సంతృప్తినివ్వదు మరియు సరిపడదు. త్రిభుజాలలో వాటి అనురూప కోణాలు సమానమైన = వాటి అనురూప భుజాలు అనుపాతంలో ఉంటాయి. కానీ ‘బహుభుజుల పరంగా ఇది సరిపడదు.

సిద్ధాంతములు:

ప్రశ్న 1.
త్రిభుజాల సరూపకతకు కో.కో.కో. నియమము : రెండు త్రిభుజాలలో అనురూప కోణాలు సమానంగా ఉంటే, వాటి అనురూప భుజాల నిష్పత్తులు సమానంగా ఉంటాయి. (అనుపాతంలో ఉంటాయి). ఇంకా ఆ రెండు భుజాలు సరూప త్రిభుజాలు అవుతాయి. (పేజీ నెం. 204)
సాధన.
దత్తాంశము : ∆ABC, ∆DEF లలో ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
సారాంశము : \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)
నిర్మాణము : AB = DP మరియు AC = DQ అగునట్లు DE మరియు DF లపై , వరుసగా బిందువులు P మరియు Q లను గుర్తించుము. P, Q లను కలుపుము.

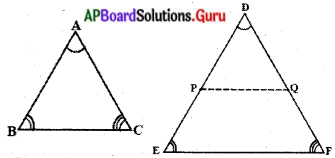
ఉపపత్తి : ∆ABC = ∆DPQ (భు.కో.భు. నియమం నుండి)
దీని నుండి ∠B = ∠P = ∠E మరియు PQ || EF (ఉప ప్రాథమిక సిద్ధాంతం నుండి)
∴ \(\frac{\mathrm{DP}}{\mathrm{PE}}=\frac{\mathrm{DQ}}{\mathrm{QF}}\) (ప్రాథమిక సిద్ధాంతం నుండి)
అనగా \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) (ప్రాథమిక సిద్ధాంతం నుండి)
అదే విధంగా \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}\) కాబట్టి
\(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{AC}}{\mathrm{DF}}\)

ప్రశ్న 2.
త్రిభుజాల సరూపకతకు భు.భు.భు.. నియమము : రెండు త్రిభుజాలలో, ఒక త్రిభుజములోని భుజాలు వేరొక త్రిభుజములోని భుజాలకు అనుపాతములో వున్న ఆ రెండు త్రిభుజాలలోని అనురూప కోణాలు సమానము ఇంకా ఆ రెండు త్రిభుజాలు సరూపాలు. (పేజీ నెం. 205)
సాధన.
దత్తాంశము : \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{BC}}{\mathrm{EF}}=\frac{\mathrm{CA}}{\mathrm{FD}}\) (< 1) అగునట్లు ∆ABC మరియు ∆DEF లను తీసుకొనుము.
సారాంశము : ∠A = ∠D, ∠B = ∠E, ∠C = ∠F.

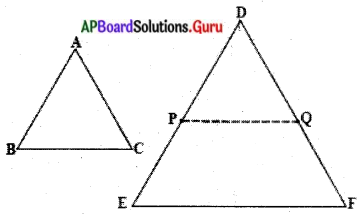
నిర్మాణము :. AB = DP మరియు AC = DQ అగునట్లు DE, DF లపై వరుసగా P మరియు Q బిందువులను గుర్తించుము, P, Q లను కలుపుము.
ఉపపత్తి : \(\frac{\mathrm{DP}}{\mathrm{PE}}=\frac{\mathrm{DQ}}{\mathrm{QF}}\) మరియు PQ || EF (ప్రాథమిక అనుపాత సిద్ధాంతం నుండి)
కావున ∠P = ∠E మరియు ∠Q = ∠F (ఆసన్న కోణాలు)
∴ \(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}=\frac{\mathrm{PQ}}{\mathrm{EF}}\)
కానీ \(\frac{\mathrm{DP}}{\mathrm{DE}}=\frac{\mathrm{DQ}}{\mathrm{DF}}=\frac{\mathrm{BC}}{\mathrm{EF}}\)
కానీ BC = PQ (నిర్మాణం నుండి)
∆ABC ≅ ∆DPQ (భు.భు.భు. సరూపకత నుండి)
కావున ∠A = ∠D, ∠B = ∠E మరియు ∠C = ∠F (కో.కో.కో. సరూపకత నుండి).

ప్రశ్న 3.
త్రిభుజాల సరూపకతకు భు.కో.భు. నియమము :
ఒక త్రిభుజములోని ఒక కోణము, వేరొక త్రిభుజములోని ఒక కోణమునకు సమానమై, ఈ కోణాలను కలిగి ఉన్న ∠A = ∠D భుజాలు అనుపాతంలో ఉంటే ఆ రెండు త్రిభుజాలు సరూపాలు. (పేజీ నెం. 206)
సాధన.
దత్తాంశము : ∆ABC మరియు ∆DEF లలో \(\frac{\mathrm{AB}}{\mathrm{DE}}=\frac{\mathrm{AC}}{\mathrm{DF}}\) (< 1) మరియు ∠A = ∠D.

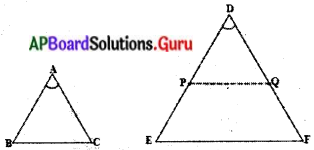
సారాంశము : ∆ABC ~ ∆DEF
నిర్మాణము : AB = DP మరియు AC = DQ అగునట్లు DE, DF భుజాలపై వరుసగా P, Q, బిందువులను గుర్తించుము. P, Q లను కలుపుము.
ఉపపత్తి : PQ || EF మరియు ∆ABC = ∆DPO
కావున ∠A = ∠D, ∠B = ∠P, ∠C = ∠Q
∴ ∆ABC ~ ∆DEF.

సిద్ధాంతములు:

ప్రశ్న 1.
రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానము. (పేజీ నెం. 211)
సాధన:

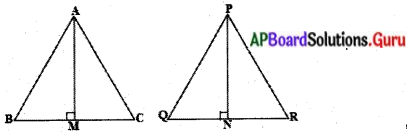
దత్తాంశము : ∆ABC ~ ∆PQR
సారాంశము :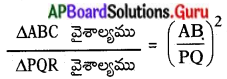
= \(\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{CA}}{\mathrm{RP}}\right)^{2}\)
నిర్మాణము : AM ⊥ BC మరియు PN ⊥ QR గీయండి.

ఉపపతి :
= \(\frac{\mathrm{BC} \times \mathrm{AM}}{\mathrm{QR} \times \mathrm{PN}}\) ………………. (1)
∆ABM మరియు ∆PQN లలో :
∠B = ∠Q (∵ ∆ABC ~ ∆POR)
∠M = ∠N = 90°
∆ABM ~ ∆PON (కో.కో.సరూపనియమం)
\(\frac{\mathrm{AM}}{\mathrm{PN}}=\frac{\mathrm{AB}}{\mathrm{PQ}}\) ……… (2)
ఇంకా ∆ABC ~ ∆PQR (దత్తాంశము)
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AC}}{\mathrm{PR}}\) …….. (3)
∴
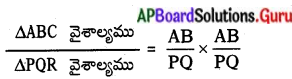
(1), (2), (3) ల నుండి = \(\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}\)
సమీకరణము (3) నుండి

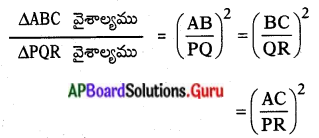
సిద్ధాంతము నిరూపించబడినది.

ఇవి చేయండి:

ప్రశ్న 1.
∆ACBలో, ∠C = 90°, CD ⊥ AB అయిన \(\frac{B C^{2}}{A C^{2}}=\frac{B D}{A D}\) అని నిరూపించండి., (పేజీ నెం. 218)
సాధన.

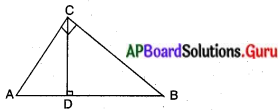
∆ADC మరియు ∆CDB లు సరూపాలు

\(\frac{\mathrm{BC}^{2}}{\mathrm{AC}^{2}}=\frac{\mathrm{BD}}{\mathrm{AD}}\)
(సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము]

ప్రశ్న 2.
15 మీటర్ల పొడవుగల ఒక నిచ్చెన రోడ్డుపై ఒక వైపున ఉన్న భవనంపై నేల నుండి 9 మీటర్ల ఎత్తున గల కిటికీని తాకింది. నిచ్చెన అడుగుభాగమును అదే ప్రదేశములో ఉంచి, నిచ్చెనను రోడ్డుకు అవతలి వైపున ఉన్న భవనముకు ఆనించగా అది 12 మీ. ఎత్తున గల కిటికీని తాకింది. అయిన ఆ రోడ్డు వెడల్పును కనుగొనుము. (పేజీ నెం. 218)
సాధన.
A మరియు D లు రోడ్డుపై ఒకవైపునున్న కిటికీలు. పైథాగరస్ సిద్దాంతం నుండి
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81.
BC² = √144 = 12

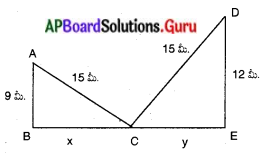
అదే విధముగా CD² = DE² + CE²
⇒ 15² = 12² + CE²
⇒ CE² = 225 – 144
⇒ CE² = 181 = 9
రోడ్డు వెడల్పు (BE) = BC + CE = 12 + 9 = 21 మీ.

ప్రశ్న 3.
ఇచ్చిన పటంలో AD ⊥ BC అయిన AB² + CD² = BD² + AC² అని చూపండి. (పేజీ నెం. 219)

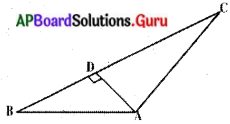
సాధన.
దత్తాంశము : ∆ABCE, AD ⊥ BC.
సారాంశము : AB² + CD² = BD² + AC²
ఉపపతి : ∆ABD ఒక లంబకోణ త్రిభుజము AB² – BD² = AD² ………… (1)
∆ACD ఒక లంబకోణ త్రిభుజము AC² – CD² = AD²
(1) మరియు (2) ల నుండి
AB² – BD² = AC² – CD²
AB² + CD² = BD² + AC² ……….. (2)

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజము మూడు భుజాల కొలతలు పూర్ణ సంఖ్యలైనపుడు కనీసము ఒకటి తప్పనిసరిగా సరిసంఖ్య అవుతుంది. ఎందుకు ? మీ మిత్రులతో మరియు ఉపాధ్యాయులతో చర్చించుము. (పేజీ నెం. 215)
సాధన.
దత్తాంశము : ఒక లంబకోణ త్రిభుజపు మూడు భుజాల కొలతలు పూర్ణ సంఖ్యలు.
సారాంశము : ఒక భుజము తప్పనిసరిగా సరిసంఖ్య.
సందర్భం – (i) : త్రిభుజ భుజాలు 3, 4, 5 లు పైథాగోరియన్ త్రికములు అయిన వాటిలో ‘4’ ఒక . సరిసంఖ్య కావున ఇచ్చిన ప్రవచనము సత్యము.
సందర్భం – (ii) : భుజాల కొలతలు పూర్ణ సంఖ్యల గుణకాలైన 3n, an మరియు 5n లు అగును. మరియు ‘4n’ ఒక సరిసంఖ్య.
∴ ఇచ్చిన ప్రవచనము సత్యము.
సందర్భం – (iii) : ఒక భుజము కొలత ‘n’ బేసి సంఖ్య అయిన n \(\frac{\mathrm{n}^{2}+1}{2}\) మరియు \(\frac{\mathrm{n}^{2}-1}{2}\) భుజాల కొలతలు అగును.
అదే విధముగా \(\frac{\mathrm{n}^{2}+1}{2}\) ఒక సరి సంఖ్య.
[∵ n = 2k + 1 ,
n² = (2k + 1)² = 4k² + 4k + 1
n² – 1 = 4k² + 4k + 1 – 1
= 4 (k² + k)
= 2 (2k² + 2k) సరిసంఖ్య
∴ ఏ సందర్భంలోనైనా ఇచ్చిన ప్రవచనము సత్యము.

సిద్ధాంతములు :

ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజములో, లంబకోణము కలిగిన శీర్షము నుండి కర్ణానికి లంబము గీసిన, ఆ లంబానికి ఇరువైపులా ఏర్పడిన త్రిభుజాలు, ఇచ్చిన త్రిభుజానికి సరూపాలు మరియు అవి ఒకదానికొకటి కూడా సరూపాలు. (పేజీ నెం. 215)
సాధన.
ఉపపత్తి : ABCలంబకోణ త్రిభుజములో, లంబకోణము కలిగిన శీర్షము B.
B నుండి కర్ణము AC కి గీసిన లంబము BD.
∆ADB మరియు ∆ABCలలో ∠A = ∠A

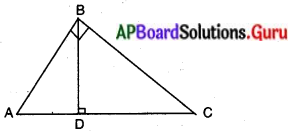
మరియు ∠ADB = ∠ABC (ప్రతికోణం 909)
కావున ∆ADB ~ ∆ABC (కో.కో.కో సరూపకత) ……….. (1)
అదేవిధంగా, ∆BDC ~ ∆ABC (కో.కో.కో సరూపకత) ……. (2)
(1), (2) ల నుండి లంబము BD కి ఇరువైపులా నున్న త్రిభుజాలు మొత్తము త్రిభుజము ∆ABC కి సరూపాలు.
ఇంకా ∆ADB ~ ∆ABC
∆BDC ~ ∆ABC
కావున ∆ADB ~ ∆BDC.

ప్రశ్న 2.
బౌధాయన సిద్ధాంతము (పైథాగరస్ సిద్ధాంతము) : ఒక లంబకోణ త్రిభుజములో కర్ణము పొడవు యొక్క వర్గము, మిగిలిన రెండు భుజాల వర్గాల మొత్తానికి సమానం. (పేజీ నెం. 215)
సాధన.
దత్తాంశము : లంబకోణ త్రిభుజము ABC లో లంబ కోణాన్ని కలిగిన శీర్షము B.
సారాంశము : AC² = AB² + BC²
నిర్మాణము : BD ⊥ AC గీయుము.
ఉపపత్తి : ∆ADB ~ ∆ABC

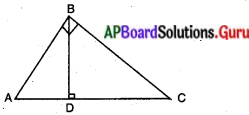
(భుజాలు అనుపాతంలో ఉంటాయి)

⇒ \(\frac{\mathrm{AD}}{\mathrm{AB}}=\frac{\mathrm{AB}}{\mathrm{AC}}\)
AD. AC = AB²
ఇంకా, ∆BDC ~ ∆ABC ……… (1)
⇒ \(\frac{\mathrm{CD}}{\mathrm{BC}}=\frac{\mathrm{BC}}{\mathrm{AC}}\)
CD. AC = BC² ……….. (2)
(1), (2) లను కలుపగా
AD . AC + CD. AC = AB² + BC²
AC (AD + CD) = AB² + BC²
AC . AC = AB² + BC²
[AC² = AB² + BC²].

ప్రశ్న 3.
పైథాగరస్ సిద్ధాంత విపర్యయము : –
ఒక త్రిభుజములో ఒక భుజము పొడవు యొక్క వర్గము మిగిలిన రెండు భుజాల పొడవుల వర్గాల మొత్తానికి సమానమైన, మొదటి భుజానికి ఎదురుగా ఉండే కోణము లంబకోణము. (పేజీ నెం. 216)
సాధన.
దత్తాంశము : ∆ABCలో AC² = AB² + BC²
సారాంశము : ∠B = 90° .

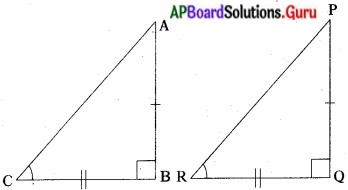
నిర్మాణము : PQ = AB మరియు QR = BC అగునట్లు Q వద్ద లంబకోణము ఉండే లంబకోణ త్రిభుజము POR ని నిర్మించుము.
ఉపపత్తి : ∆PQR లో PR² = PQ² + QR²
(∠Q = 90° కావున పైథాగరస్ సిద్ధాంతము ప్రకారం)
PR² = AB² + BC² (నిర్మాణము నుండి) ………………. (1)
కానీ AC² = AB² + BC² (దత్తాంశము) …………… (2)
AC = PR (1), (2) ల నుండి
ఇప్పుడు ∆ABC, ∆PQR లలో
AB = PQ (నిర్మాణము)
BC = QR (నిర్మాణము)
AC = PR (నిరూపితము).

ఉదాహరణలు:

ప్రశ్న 1.
∆ABC లో, DE || BC మరియు \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}\) AC = 5.6 సె.మీ. అయిన AE విలువ ఎంత? (పేజీ నెం. 199)
సాధన
∆ABC లో, DE || BC
⇒ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి)
కానీ \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{3}{5}\), కావున \(\frac{\mathrm{AE}}{\mathrm{EC}}=\frac{3}{5}\)
AC = 5.6 సెం.మీ. మరియు AE : EC = 3:5
\(\frac{\mathrm{AE}}{\mathrm{AC}-\mathrm{AE}}=\frac{3}{5}\)
\(\frac{\mathrm{AE}}{5.6-\mathrm{AE}}=\frac{3}{5}\) (అడ్డగుణకారం చేయగా)
5AE = (3 × 5.6) – 3AE
8AE = 16.8
AE = \(\frac{16.8}{8}\) = 2.1 సెం.మీ.

ప్రశ్న 2.
ఇచ్చిన పటంలో LM || AB AL = x – 3, AC = 2x, BM = x – 2 మరియు BC = 2x + 3 అయిన X విలువను కనుగొనుము. (పేజీ నెం. 200)

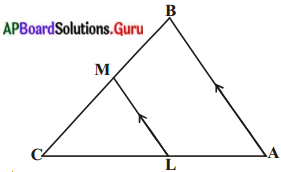
సాధన.
∆ABC లో, LM || AB
⇒ \(\frac{\mathrm{AL}}{\mathrm{LC}}=\frac{\mathrm{BM}}{\mathrm{MC}}\) (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి) x -3
\(\frac{x-3}{2 x-(x-3)}=\frac{x-2}{(2 x+3)-(x-2)}\)
\(\frac{x-3}{x+3}=\frac{x-2}{x+5}\)
(x – 3) (x + 5) = (x – 2) (x + 3) (అడ్డగుణకారం చేయగా)
x² + 2x – 15 = x² + x – 6
⇒ 2x – 15 = x – 6
∴ x = 9.

ప్రశ్న 3.
ఒక చతుర్భుజము ABCD లో కర్ణములు ‘O’ బిందువు వద్ద ఖండించుకొనును మరియు \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) అయిన అది ఒక ట్రెపీజియం అని చూపండి. (పేజీ నెం. 200)
సాధన.
దత్తాంశము : చతుర్భుజము ABCD లో, \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\)
సారాంశము : ABCD ఒక ట్రెపీజియం.
నిర్మాణము : ‘0’ బిందువు గుండా ABకి సమాంతరంగా రేఖను గీసిన అది DA ను బిందువు ‘X’ వద్ద ఖండించును.
ఉపపత్తి : ∆DABలో, XO || AB (నిర్మాణము నుండి)
⇒ \(\frac{\mathrm{DX}}{\mathrm{XA}}=\frac{\mathrm{DO}}{\mathrm{OB}}\) (ప్రాథమిక అనుపాత సిద్ధాంతము నుండి)

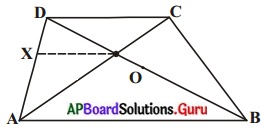
\(\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) ………….. (1)

కొని \(\frac{\mathrm{AO}}{\mathrm{BO}}=\frac{\mathrm{CO}}{\mathrm{DO}}\) (దత్తాంశము)
\(\frac{\mathrm{AO}}{\mathrm{CO}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) …………. (2)
(1) (2) ల నుండి
\(\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{AO}}{\mathrm{CO}}\)
∆ADC లో, \(\frac{\mathrm{AX}}{\mathrm{XD}}=\frac{\mathrm{AO}}{\mathrm{CO}}\) అగునట్లు XO రేఖ ఉన్నది.
⇒ XO || DC (ప్రాథమిక అనుపాత సిద్ధాంతము విపర్యయము నుండి)
⇒ AB || DC చతుర్భుజము ABCDలో, AB || DC
⇒ ABCD ఒక ట్రెపీజియం (నిర్వచనం ప్రకారం) కావున రుజువు చేయబడినది.

ప్రశ్న 4.
ట్రెపీజియం ABCD లో, AB || DC E మరియు F బిందువులు వరుసగా EF || AB ను కుట్లు సమాంతరం కాని భుజాలు AD, BC లపై ఉన్నవి. అయిన \(\frac{\mathbf{A E}}{\mathbf{E D}}=\frac{\mathbf{B F}}{\mathbf{F C}}\) అని చూపండి. (పేజీ నెం. 201)
సాధన.
A, C బిందువులను కలుపగా ఏర్పడిన రేఖాఖండము EF ను G వద్ద ఖండించినది.
AB || DC మరియు EF || AB (దత్తాంశము)
⇒ EF || DC (ఒకే రేఖకు సమాంతరంగా ఉన్న రేఖలు సమాంతరాలు)

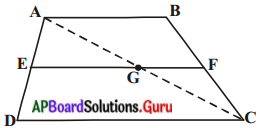
∆ADC లో, EG || DC
కావున \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{AG}}{\mathrm{GC}}\)
(ప్రాథమిక అనుపాత సిద్ధాంత ప్రకారం) ……… (1)
అదే విధంగా, ∆CAB లో, GF || AB
\(\frac{\mathrm{CG}}{\mathrm{GA}}=\frac{\mathrm{CF}}{\mathrm{FB}}\) (ప్రాథమిక అనుపాత సిద్ధాంత ప్రకారం)
అనగా \(\frac{\mathrm{AG}}{\mathrm{GC}}=\frac{\mathrm{BF}}{\mathrm{FC}}\) ………. (2)
(1) (2) ల నుండి, \(\frac{\mathrm{AE}}{\mathrm{ED}}=\frac{\mathrm{BF}}{\mathrm{FC}}\).

ప్రశ్న 5.
1.65మీ. పొడవు గల ఒక వ్యక్తి నీడ పొడవు 1.8 మీ. అదే సమయంలో, ఒక దీపస్తంభము 5.4 మీ. పొడవు గల నీడను ఏర్పరచిన, ఆ దీపస్తంభము పొడవు ఎంత ? (పేజీ నెం. 208)

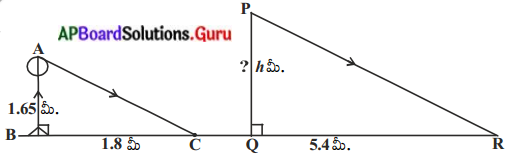
సాధన.
∆ABC మరియు ∆PCR లో
∠B = ∠Q = 90°
∠C = ∠R (AC || PR, ఏ సమయంలోనైనా సూర్యకిరణాలు సమాంతరాలు)
∆ABC ~ ∆PQR (కో కో సరూపనియమం ప్రకారం)
\(\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}\) (సరూపత్రిభుజాల అనురూపభుజాలు)
\(\frac{1.65}{\mathrm{PQ}}=\frac{1.8}{5.4}\)

PQ = \(\frac{1.65 \times 5.4}{1.8}\) = 4.95 మీ.
ఆ దీప స్తంభము ఎత్తు 4. 95 మీ.

ప్రశ్న 6.
ఒక గోపురము నుండి 87.6 మీటర్ల దూరములో నేలపై అద్దము ఊర్ధ్వ దిశలో ఉంచబడినది మరియు ఉంచిన ఆ అద్దములో ఒక వ్యక్తి గోపుర శిఖరమును చూసెను. వ్యక్తి అద్దము నుండి 0.4 మీ. దూరములో ఉన్నాడు. అతని కంటి చూపు భూమి నుండి 1.5 మీటర్ల ఎత్తులో నున్న ఆ గోపురము ఎత్తును కనుగొనుము. (పేజీ నెం. 209)

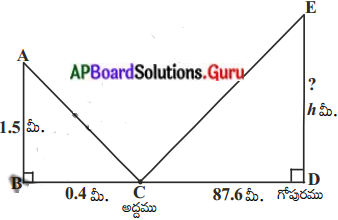
సాధన.

∆ABC మరియు ∆EDC లో ∠ABC = ∠EDC = 90° ∠BCA = ∠EDC (పతన కోణము మరియు పరావర్తన కోణములు సమానము)
∆ABC ~ ∆EDC (కోకో సరూప నియమం)
\(\frac{\mathrm{AB}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{CD}}\)

\(\frac{1.5}{\mathrm{~h}}=\frac{0.4}{87.6}\)

h = \(\frac{1.5 \times 87.6}{0.4}\) = 328.5 మీ.
కావున, ఆ గోపురము ఎత్తు 328. 5 మీ.

ప్రశ్న 7.
గోపాల్ తన ఇంటి హాలు ప్రక్క అపార్టుమెంటు పై అంతస్థులోని కిటికీ వద్ద నిలుచునే వ్యక్తులకు ఎప్పుడూ. కనిపిస్తూ ఉంటోందని ఆందోళన పడుతున్నాడు. దాని కొరకు వారికి కనిపించకుండా ఉండేటందుకు తన ఇంటి ప్రహరీ. గోడ ఎత్తు పెంచాలనుకొన్నాడు. కొలతలు పటంలో ఈయబడ్డాయి. ప్రహరీ గోడను ఎంత ఎత్తు వరకు నిర్మించాలి? (పేజీ నెం. 209)
సాధన.

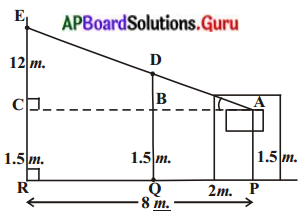
∆ABD మరియు ∆ACE లలో ∠B = ∠C = 90° ∠A = ∠A (ఉమ్మడి కోణం)
∆ABD ~ ∆ACE (కో కో సరూప నియమం)
\(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{CE}}\)
⇒ \(\frac{2}{8}=\frac{\mathrm{BD}}{1.2}\)

BD = \(\frac{2 \times 1.2}{8}=\frac{2.4}{8}\) = 0.3 మీ.
ప్రహరీగోడ కావలసిన ఎత్తు = 1.5 మీ + 0.3 మీ
1.8మీ ఎత్తు నిర్మించిన, ప్రహరీగోడ హాలు ప్రక్క ఇంటి వారికి కన్పించకుండా చేయవచ్చును.

ప్రశ్న 8.
రెండు సరూపత్రిభుజాల వైశాల్యాలు సమానమైన అవి సర్వసమాన త్రిభుజాలని చూపండి. (పేజీ నెం. 213)
సాధన.
∆ABC ~ ∆PQR

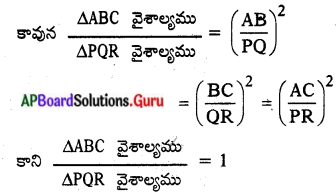
(∵ వైశాల్యాలు సమానము కావున)
\(\left(\frac{\mathrm{AB}}{\mathrm{PQ}}\right)^{2}=\left(\frac{\mathrm{BC}}{\mathrm{QR}}\right)^{2}=\left(\frac{\mathrm{AC}}{\mathrm{PR}}\right)^{2}\) = 1
కావున AB² = PQ²
BC² = QR²
AC² = PR²
దీని నుండి మనకు AB = PQ
BC = QR
AC = PR లభిస్తుంది
∆ABC = ∆POR, (భు.భు.భు. సర్వసమాన నియమం)

ప్రశ్న 9.
∆ABC ~ ∆DEF మరియు వాటి వైశాల్యాలు వరుసగా 64 చ.సెం.మీ మరియు 121 సెం.మీ. ఇంకా EF = 15.4 సెం.మీ అయిన BC కొలతను కనుగొనుము. (పేజీ నెం. 213)
సాధన.

\(\frac{64}{121}=\left(\frac{B C}{15.4}\right)^{2}\) \(\frac{8}{11}=\frac{\mathrm{BC}}{15.4}\)

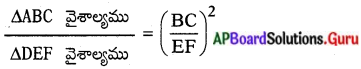
BC = \(\frac{8 \times 15.4}{11}\) = 11.2 సెం.మీ.

ప్రశ్న 10.
ట్రెపీజియం ABCDలో AB || DC. ఇంకా కర్ణములు AC, BD లు ‘0’ వద్ద ఖండించుకొంటాయి. AB = 2CD అయిన త్రిభుజములు AOB మరియు COD ల వైశాల్యముల నిష్పత్తిని కనుగొనండి. (పేజీ నెం. 213)
సాధన.

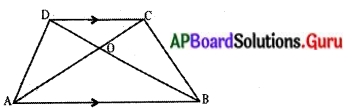
ట్రెపీజియం ABCD లో AR || DC. ఇంకా AB = 2CD.
∆AOB, ∆COD లలో ∠AOB = ∠COD (శీర్షాభిముఖ కోణాలు)
∠OAB = ∠OCD (ఏకాంతర కోణాలు)
∆AOB ~ ∆COD (కో.కో సరూప నియమం)

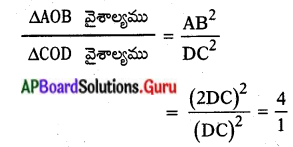
∴ ∆AOB వైశాల్యము : ∆COD వైశాల్యము = 4 : 1.

ప్రశ్న 11.
25మీ. పొడవుగల ఒక నిచ్చెన, గోడపై 20 మీ. ఎత్తున గల ఒక కిటికీని తాకుచున్నది. అయిన ఆ నిచ్చెన అడుగుభాగము నేలపై గోడ నుండి ఎంత దూరములో ఉన్నది ? (పేజీ నెం. 217)
సాధన.

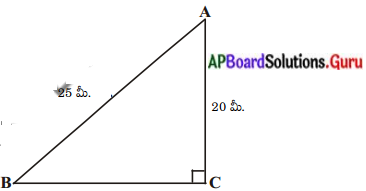
∆ABC లో ∠C = 90°.
⇒AD² = AC² + BC² (పైథాగరస్ సిద్ధాంతము)
25² = 20² + BC²
BC² = 625 – 400 = 225
BC = √225 = 15మీ.
కావున నిచ్చెన అడుగుభాగము నేలపై గోడ నుండి 15మీ. దూరములో ఉన్నది.

ప్రశ్న 12.
లంబకోణ త్రిభుజము ABC లో శీర్షము ‘A’ వద్ద లంబకోణము కలదు. BL మరియు CM లు దీనిలో మధ్యగతరేఖలు అయిన 4(BL² + CM²) = 5BC² అని చూపండి. (పేజీ నెం. 217)
సాధన.

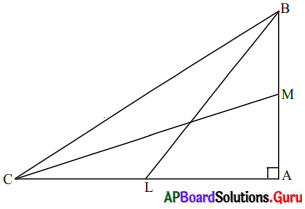
∆ABC లో ∠A = 90° BL, CM లు మధ్యగతరేఖలు
∆ABC లో, BC² = AB² + AC² …………. (1) (పైథాగరస్ సిద్ధాంతము)
∆ABL లో, BL² = AL² + AB²
కానీ BL² = \(\left(\frac{\mathrm{AC}}{2}\right)^{2}\) + AB² (∵ AC మధ్యబిందువు L కావున)
BL² = \(\frac{\mathrm{AC}^{2}}{4}\) + AB²
∴ 4BL² = AC² + 4AB² …………… (2)
∆CMA లో, CM² = AC² + AM²
CM² = AC² + \(\left(\frac{\mathrm{AB}}{2}\right)^{2}\)
(∴ AB మధ్య బిందువు M కావున)
CM² = AC² + \(\frac{\mathrm{AB}^{2}}{4}\)
4CM² = 4AC² + AB² ………….. (3)
(2), (3) లను కలుపగా ‘
4(BL ²+ CM²) = 5(AC² + AB²)
∴ 4(BL² + CM²) = 5BC² (1) నుండి.

ప్రశ్న 13.
దీర్ఘచతురస్రం ABCD అంతరంలో ఏదైనా బిందువు ‘O’ ఆయితే OB² + OD² = OA²+ OC² అని చూపండి. (పేజీ నెం. 218)
సాధన.

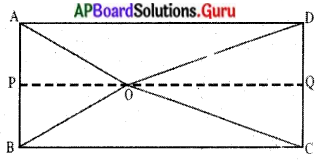
‘0’ బిందువు గుండా BC కి సమాంతరంగా ఒక రేఖను గీసిన అది AB ని P వద్ద, DC ని Q వద్ద తాకును. అపుడు PQ || BC.
∴ PQ ⊥ AB మరియు PQ ⊥ DC.
(∵ ∠B = ∠C = 90°) కావున ∠BPQ = 90° & ∠CQP = 90°
∴ BPQC మరియు APQD లు రెండు దీర్ఘచతురస్రాలు.
∆OPB నుండి OB² = BP² + O² ……… (1)
అదేవిధంగా ∆OQD నుండి OD² = OQ² + DQ² ……… (2)
∆OQC నుండి OC² = OQ² + CQ² ……………. (3)
∆OAP నుండి OA² = AP² + OP²
(1), (2) లను కలుపగా
OB² + OD² = BP² + OP² + OQ² + DQ²
= CQ² + OP² + OQ² + AP² (∵ BP = CQ మరియు DQ = AP)
= CQ² + OQ² + OP² + AP²
= OC² + OA² ((3), (4) ల నుండి)

ప్రశ్న 14.
ఒక లంబకోణ త్రిభుజములో కర్ణము, దాని అతి చిన్న భుజము రెట్టింపు కన్నా 6మీ. ఎక్కువ. మూడవ భుజము కర్ణము కన్నా 2 మీ. తక్కువ. అయిన ఆ త్రిభుజ భుజాలను కనుగొనుము: . (పేజీ నెం. 219)
సాధన.
అతి చిన్న భుజమును x మీ. అనుకొనుము.
అపుడు కర్ణము = (2x + 6) మీ. మరియు
మూడవ భుజము = (2x + 4) మీ.
పైథాగరస్ సిద్ధాంతము నుండి, (2x + 6)² = x² + (2x + 4)²
4x² + 24x + 36 = x² + 4x² + 16x + 16
x² – 8x – 20 = 0
⇒ (x – 10) (x + 2) = 0
⇒ x = 10 లేదా x = – 2
x అనేది త్రిభుజ భుజము కావున రుణవిలువ కానేరదు.
∴ x = 10
అందువలన, ఆ త్రిభుజభుజాలు 10 మీ., 26 మీ. మరియు 24 మీ.

ప్రశ్న 15.
లంబకోణ త్రిభుజము ABCలో లంబకోణము శీర్షము ‘C’ వద్ద కలదు. BC = a, CA = b, AB =’c అనుకొనుము. ఇంకా శీర్షము ‘C’ నుండి AB కి గీసిన లంబము పొడవు p అయిన (పేజీ నెం. 219)
(i) pc = ab
(ii) \(\frac{1}{p^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\) అని చూపండి.
సాధన.

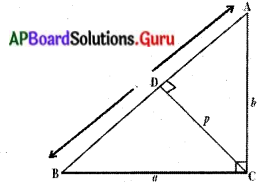
(i) CD ⊥ AB మరియు CD = p.
∆ABC వైశాల్యము \(\frac{1}{2}\) × AB × CD = \(\frac{1}{2}\) cp
అలాగే ∆ABC వైశాల్యము = \(\frac{1}{2}\) × BC × AC = \(\frac{1}{2}\) ab
\(\frac{1}{2}\) cp = \(\frac{1}{2}\) ab
⇒ cp = ab ……. (1)

(ii) లంబకోణ త్రిభుజము ABCలో లంబకోణము శీర్షము ‘C’ వద్ద కలదు.
కావున AB² = BC² + AC²
c² = a² + b²
\(\left(\frac{a b}{p}\right)^{2}\) = a² + b²
⇒ \(\frac{1}{p^{2}}=\frac{a^{2}+b^{2}}{(a b)^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}\)