AP Board 10th Class Maths Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.1

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.1 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Exercise 9.1

ప్రశ్న 1.
కింది ఖాళీలను పూరించండి.
(i) వృత్తాన్ని, ఒక స్పర్శరేఖ ………………. బిందువు (ల) వద్ద ఖండిస్తుంది.
సాధన.
ఒక

(ii) వృత్తాన్ని ఒక రేఖ రెండు వేర్వేరు బిందువుల వద్ద ఖండిస్తే దానిని ………….. అంటారు.
సాధన.
వృత్త ఛేదన రేఖ

(iii) ఒక వృత్తానికి వ్యాసం చివరి బిందువుల వద్ద గీయగల సమాంతర స్పర్శరేఖల సంఖ్య
సాధన.
2

(iv) ఒక వృత్తానికి, దాని స్పర్శరేఖకు గల ఉమ్మడి బిందువును ……….. అంటారు.
సాధన.
స్పర్శ బిందువు

(v) ఒక వృత్తానికి మనము ………… స్పర్శరేఖలను గీయగలము.
సాధన.
అనంత

ప్రశ్న 2.
5 సెం.మీ వ్యాసార్ధముగా గల వృత్తాన్ని PQస్పర్శరేఖ P వద్ద తాకింది. వృత్త కేంద్రము ‘0’ నుండి స్పర్శరేఖపై గల బిందువు Q నకు దూరము OQ = 13 సెం.మీ. అయిన PQ పొడవును కనుగొనుము.
సాధన.

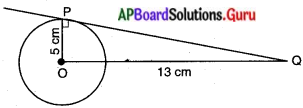
ఇచ్చిన వృత్త వ్యాసార్ధం r = OP = 5 సెం.మీ.
\(\overline{\mathrm{OQ}}\) = 12 సెం.మీ.
పటం నుండి పైథాగరస్ సిద్ధాంతం ప్రకారం OP² + PQ² = OQ²
PQ² = OQ² – OP²
∴ PQ = \(\sqrt{\mathrm{OQ}^{2}-\mathrm{OP}^{2}}=\sqrt{13^{2}-5^{2}}\)
= \(\sqrt{169-25}=\sqrt{144}\) = 12
PQ = 12 cm.

ప్రశ్న 3.
ఒక వృత్తాన్ని గీయండి. వృత్తానికి బాహ్యంలో గల ఒక రేఖకు సమాంతరముగా ఒక స్పర్శరేఖనూ, ఒక ఛేదన రేఖను గీయండి.
సాధన..

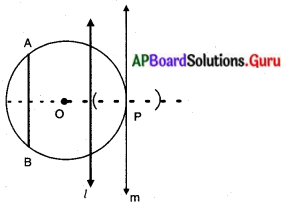
నిర్మాణ క్రమం :
(1) తగు వ్యాసార్థంచే వృత్తాన్ని నిర్మించవలెను.
(2) ఆ వృత్తానికి AB బ్యాను గీయవలెను.
(3) AB జ్యా కు సమాంతరంగా ఒక ఛేదన రేఖ 1 ను గీయవలెను.
(4) AB జ్యాకు మరియొక సమాంతరరేఖ m ను వృత్తానికి ‘P’ అను బిందువు వద్ద గీచిన, అది వృత్తానికి స్పర్శరేఖ అగును.

ప్రశ్న 4.
9 సెం.మీ వ్యాసార్ధముగా గల వృత్తానికి, దాని కేంద్రం నుండి 15 సెం.మీ దూరంలో ఒక బిందువు కలదు. అయిన ఆ బిందువు నుండి వృత్తానికి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనండి.
సాధన.

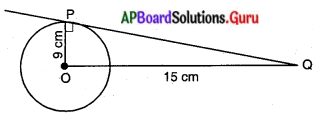
పటం నుండి వృత్త వ్యాసార్ధం (r) = OP = 9 సెం.మీ.

కేంద్రం నుండి Q బిందువుకు గల దూరం d = \(\overline{\mathrm{OQ}}\) = 15 సెం.మీ.
స్పర్శరేఖ పొడవు = PQ = \(\sqrt{\mathrm{d}^{2}-\mathrm{r}^{2}}\)
= \(\sqrt{15^{2}-9^{2}}\)
= \(\sqrt{225-81}\)
స్పర్శరేఖ పొడవు = √144 = 12 సెం.మీ.

ప్రశ్న 5.
ఒక వృత్త వ్యాసము చివరి బిందువుల వద్ద గీయబడిన స్పర్శరేఖలు సమాంతరమని చూపండి.
సాధన.
నిరూపణ (దత్తాంశం): ‘O’ కేంద్రంగా గల వృత్త వ్యాసం AB.
PQ, RS లు వృత్తానికి వరుసగా A, B బిందువుల వద్ద గీచిన స్పర్శరేఖలు.
సారాంశం : PQ || RS.

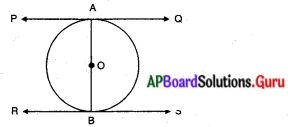
ఉపపత్తి : ‘O’ కేంద్రంగా గల వృత్తానికి OA వ్యాసార్ధం, PQ స్పర్శరేఖ.
∴ OA ⊥ PQ ……………..(1)
[∵ వ్యాసార్ధం, స్పర్శరేఖకు లంబంగా ఉండును.]
అదే విధంగా OB ⊥ RS …………. (2)
కాని OA మరియు OB, AB యొక్క భాగాలు. AB ⊥ PQ మరియు AB ⊥ RS.
∴ PQ || RS. [∵ ఒకే రేఖతో లంబంగా ఉండు రెండు సరళరేఖలు ఒకదానికొకటి సమాంతరంగా ఉండును.]
(లేదా) ఉపపత్తి : ‘O’ కేంద్రంగా గల ‘వృత్తానికి A వద్ద PQ స్పర్శరేఖ.
∠OAQ = 90°
అదే విధంగా, ∠OBS = 90°
∠OAQ + ∠OBS = 90° + 90° = 180°
∴ PQ || RS. (∵ తిర్యగ్రేఖకు ఒకే వైపునగల అంతర కోణాల మొత్తం 180° అయిన అవి సమాంతర రేఖలగును.)