AP Board 10th Class Maths Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
i. ఏదైనా వ్యాసార్ధంతో వృత్తం గీయండి. ఏవైనా వేర్వేరు బిందువుల వద్ద నాలుగు స్పర్శరేఖలను గీయండి. ఇంకనూ ఈ వృత్తానికి ఎన్ని సరళరేఖలను గీయవచ్చు? (పేజీ నెం. 226)
సాధన.

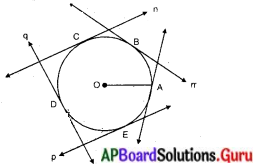
‘O’ అనునది వృత్త కేంద్రం. OA వృత్త వ్యాసార్ధం (r). l, m, n, p మరియు qలు వృత్తానికి A, B, C, D, E ల వద్ద గీచిన స్పర్శ రేఖలు.
∴ ఒక వృత్తానికి అనంతమైన స్పర్శ రేఖలు గీయవచ్చు.

ii. వృత్తానికి బాహ్యంలో ఇచ్చిన బిందువు నుండి ఎన్ని స్పర్శరేఖలను నీవు గీయగలవు ?
సాధన.

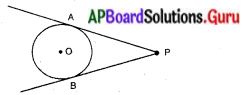
బాహ్య బిందువు నుండి వృత్తానికి రెండు స్పర్శరేఖలు మాత్రమే గీయగలం. PA, PB లు వృత్తానికి గీచిన రెండు స్పర్శరేఖలు.

iii. పటంలో ఏ రేఖలు వృత్తానికి స్పర్శరేఖలు అవుతాయి?
సాధన.

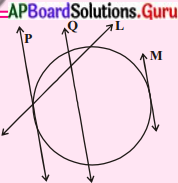
p మరియు m లు వృత్తానికి స్పర్శరేఖలు అగును.

ప్రశ్న 2.
ఒక కాగితముపై వృత్తాన్ని గీచి, దానిపై PQ ఛేదన రేఖను పటములో చూపిన విధంగా గీయండి. ఈ ఛేదనరేఖకు సమాంతరముగా ఇరువైపులా మరికొన్ని రేఖలను గీయండి. ఛేదనరేఖ వృత్తకేంద్రము వైపుకు జరుగుతున్న కొలదీ ‘వృత్త జ్యా’ పొడవు ఏమైంది ? ఏది పెద్ద జ్యా? ఒకదానికొకటి సమాంతరంగా ఉండే (పేజీ నెం. 227)

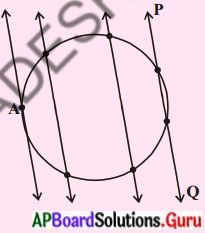
సాధన.
(i)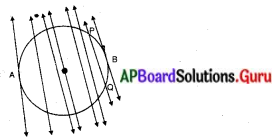

(ii) పై పటం నుండి ఛేదనరేఖ , వృత్త కేంద్రం వైపుకు జరుగుతున్న కొద్దీ వాని పొడవులు పెరుగును.
(iii) జ్యాలలో అతి పొడవైనది వృత్త కేంద్రం గుండా పోయే వ్యాసం.
(iv) వృత్తానికి గీచిన స్పర్శరేఖకు సమాంతరంగా ఒకే ఒక స్పర్శరేఖను గీయగలం.

ప్రయత్నించండి:

ఒక వృత్తముపై గల ఏదైనా బిందువు గుండా గీయబడిన స్పర్శరేఖ, ఆ స్పర్శ బిందువు వద్ద వ్యాసార్ధానికి లంబముగా ఉంటుంది.

ప్రశ్న 1.
పై సిద్ధాంతము యొక్క విపర్యయంను నీవు ఏవిధంగా నిరూపిస్తావు ? (పేజీ నెం. 228)
సాధన.
నిరూపణ :
దశాంశం : ‘0’ కేంద్రంగా గల వృత్తంలో OA అనునది AT సరళరేఖకు ‘A’ వద్ద లంబంగా కలదు.
సారాంశం : AT వృత్తానికి ‘A’ వద్ద ఒక స్పర్శరేఖ.
నిర్మాణం : AT స్పర్శరేఖ కానిచో AT (పొడిగించగా) వృత్తమునకు మరియొక బిందువు వద్ద కలియును. ఆ విధంగా P వద్ద కలిసెను అనుకొనుము. ), P లను కలిపితిని. (P, AT పై ఒక బిందువు.)

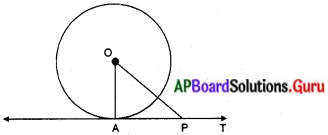
ఉపపత్తి : OA = OP (వ్యాసార్ధాలు) కావున ∠OAP = ∠OPA
కానీ ∠OPA = 90°
ఒక త్రిభుజంలో రెండు లంబకోణాలు ఉండవు కనుక ఇది అసంభవం. కనుక AT స్పర్శరేఖ కాదను ఊహ సరికాదు.
∴ AT, వృత్తానికి స్పర్శరేఖ అగును.

ప్రశ్న 2.
వృత్త కేంద్రము తెలియని సందర్భములో వృత్తముపై గల బిందువు గుండా వృత్తానికి స్పర్శరేఖను ఎలా గీస్తావు ?
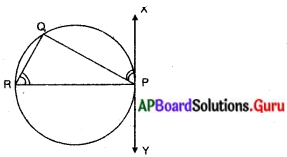
సూచన : ∠QPX మరియు ∠PRQ అనే సమాన కోణాలను నిర్మించుము. నిర్మాణ క్రమాన్ని వివరించండి. (పేజీ నెం. 229)

సాధన.
నిర్మాణ క్రమం :
1) వృత్తంపై P అను బిందువు గుండా PR అను ఒక జ్యాను గీచితిని.
2) ∠PRQ ను నిర్మించి కొలిచితిని.
3) ∠PRQ కు సమానమైన కోణాన్ని PX పై P వద్ద నిర్మించితిని.
4) PX ను ఇరువైపులా పొడిగించితిని.
∴ \(\overline{\mathrm{XY}}\) వృత్తానికి P వద్ద ఒక స్పర్శరేఖ.
గమనిక :
జ్యాకు మరియు స్పర్శరేఖకు మధ్యగల కోణం దాని అనురూప వృత్త ఖండంలోని కోణానికి సమానం.

నిర్మాణ క్రమం :

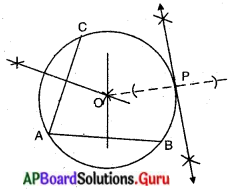
1) ఇచ్చిన వృత్తానికి AB మరియు AC అను రెండు జ్యాలు గీయుము.

2) AB మరియు AC లపైకి గీయబడిన లంబ సమద్విఖండనరేఖల మిళితబిందువు వృత్త కేంద్రాన్ని ఏకీభవిస్తుంది.
3) ‘O’ వృత్త కేంద్రం అనుకుంటే 0, P లను కలుపుము.
4) OP పైకి ఒక లంబాన్ని P వద్ద గీచి దాని ఇరువైపులా పొడిగించుము.
∴ కావలసిన స్పర్శరేఖ P వద్ద ఏర్పడినది.

సిద్ధాంతము – 1:

ఒక వృత్తముపై గల ఏదైనా బిందువు గుండా గీయబడిన స్పర్శరేఖ, ఆ స్పర్శబిందువు వద్ద వ్యాసార్ధానికి లంబముగా ఉంటుంది. (పేజీ నెం. 227)

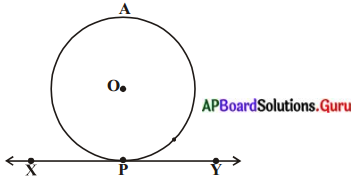
దత్తాంశము : ‘O’ కేంద్రముగా గల వృత్తానికి స్పర్శరేఖ XY, P బిందువు AB గుండా గీయబడింది.
సారాంశము : OP, XY నకు లంబము అనగా (OP ⊥ XY).
ఉపపత్తి : ఇచ్చట మనము నిరూపించవలసిన వాక్యాన్ని తప్పుగా భావించి ఒక కొత్త ప్రతిపాదన చేస్తాము. ఈ ప్రతిపాదన లేదా ఊహ విరుద్ధతకు దారితీస్తుంది. ఈ పద్ధతిలో మనం OP అనేది XY పైన -P కాకుండా మరొక బిందువు Q ను తీసుకొని 0Q ను కలుపుదాం.

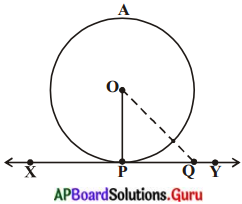
Q బిందువు కచ్చితంగా వృత్తానికి బాహ్యంలోనే ఉంటుంది (ఎలా ?) (Q ఒకవేళ వృత్త అంతరంలో వుంటే XY అనేది వృత్తానికి స్పర్శరేఖ కాకుండా ఛేదన రేఖ అవుతుందని గమనించండి.)
అందువలన, OQ అనేది వ్యాసార్ధం OQ అనేది వ్యాసార్ధం OP కన్నా పొడవుగా వుంటుంది
అంటే OQ > OP
XY పైన గల ఏ ఇతర బిందువులకైన ఇది వర్తిస్తుంది. అందుచే ‘0’ నుండి XY పైకి గీయబడిన అన్ని పొడవులలో OP మాత్రమే మిక్కిలి చిన్నది అగును.
కనుక మనం ఊహించినట్లుగా OP, XY కు లంబంగా వుండదు అనే భావన తప్పు అని తేలినది. అందువలన OP XY రేఖకు లంబం.
గమనిక :
వృత్త వ్యాసార్ధానికి స్పర్శ బిందువు గుండా గీయబడిన’ రేఖను ఆ వృత్తానికి ఆ బిందువు వద్ద అభిలంబం (Normal) అని కూడా అంటారు.

ప్రయత్నంచండి:

ప్రశ్న 1.
పైథాగరస్ సిద్ధాంతమును ఉపయోగించి వృత్తానికి బాహ్య బిందువు గుండా గీయబడిన స్పర్శరేఖల పొడవులు సమానము అను సిద్ధాంతమును నిరూపించడానికి ఉపపత్తిని రాయండి. (పేజీ నెం. 231)
సాధన.
నిరూపణ :
దత్తాంశం ‘: ‘0’ కేంద్రంగా గల వృత్తానికి PA మరియు PB లు బాహ్య బిందువు P నుండి గీచిన స్పర్శరేఖలు.

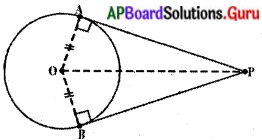
సారాంశం : PA = PB
ఉపపత్తి: ∆AOP నుండి ∠OAP = 90°,
∴ AP² = OP² – OA² (పైథాగరస్ సిద్ధాంతం నుండి)
= OP² – OB² [∵ OA = OB, వృత్త వ్యాసార్ధాలు సమానం]
= BP²
⇒ AP² = BP²
⇒ AP = BP
∴ బాహ్య బిందువు నుండి వృత్తానికి గీచిన స్పర్శ – రేఖల పొడవులు సమానాలు.

ప్రశ్న 2.
∠BOA = 120° అగునట్లు OA మరియు OB వ్యాసార్ధాలను గీయండి. ∠BOA కు సమద్విఖండన రేఖను గీచి DA, OB లకు A మరియు B ల వద్ద లంబరేఖలు గీయండి. ఈ రేఖలు ∠BOA సమద్విఖండన రేఖను బాహ్యబిందువు వద్ద ఖండిస్తాయి. వీటినే మనకు కావల్సిన స్పర్శరేఖలుగా తీసుకొనవచ్చు. నిర్మాణము చేయండి.
సమర్థించండి. (పేజీ నెం. 235)
సాధన.

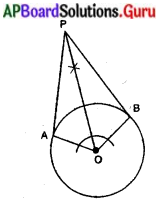
సరిచూచుట :
OA ⊥ OP మరియు OB ⊥ PB
∆OAP, ∆OBP ల నుండి OA = OB
∠OAP = ∠OBP
OP = OP
∴ ∆OAP = ∆OBP
∴ PA = PB. [∵ అనురూప భుజాలు సమానాలు]

సుధాంతము – 2:
వృత్తానికి బాహ్యబిందువు గుండా గీయబడిన స్పర్శరేఖల పొడవులు సమానము. (పేజీ నెం. 231)
సాధన.
దత్తాంశము : ‘O’ కేంద్రముగా గల వృత్తానికి, P అనే బిందువు బాహ్యంలో కలదు. P బిందువు గుండా వృత్తానికి గీయబడిన స్పర్శరేఖలు PA మరియు PB
సారాంశము : PA = PB
ఉపపత్తి : OA, OB మరియు OP లను కలపండి. ∠OAP = ∠OBP = 90°

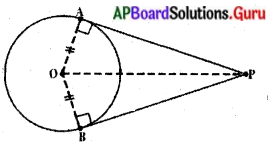
ఇప్పుడు ∆OAP మరియు ∆OBP లలో, OA = OB (ఒకే వృత్త వ్యాసార్ధాలు) OP = OP (ఉమ్మడి భుజము)
అందువలన లం.క.భు సర్వసమాన స్వీకృతం ప్రకారము ∆OAP ≅ ∆OBP అయినది.
దీని నుండి PA = PB అగును (సర్వసమాన త్రిభుజాలలో సరూపభాగాలు) నిరూపించబడినది.

ప్రవచనములు :

ప్రశ్న 1.
వృత్తానికి బాహ్యబిందువు నుండి గీయబడిన స్పర్శరేఖల మధ్య ఏర్పడే కోణ సమద్విఖండన రేఖపై ఆ వృత్తం యొక్క కేంద్రం వుంటుంది. దీనిని ఏవిధంగా నిరూపించగలమో ఆలోచించండి. (పేజీ నెం. 232)
సాధన.
నిరూపణ :’O’ కేంద్రముగా గల వృత్తానికి P ఒక బాహ్యబిందువు. PQ మరియు PR లు. P నుండి వృత్తం పైకి గీయబడిన స్పర్శరేఖలు.
OQ మరియు OR లను కలపండి , త్రిభుజాలు OQP మరియు ORP లు సర్వసమానాలు, ఎందుకంటే

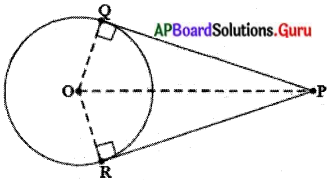
∠OQP = ∠ORP = 90 (సిద్దాంతం 1 ప్రకారం వృత్త వ్యాసార్ధానికి, స్పర్శరేఖకు మధ్య ఏర్పడిన కోణము లంబకోణం .)
OQ = OR (వ్యాసార్ధాలు)
OP ఉమ్మడి భుజము సర్వసమాన త్రిభుజాల సరూప భుజాలు సమానము కావున ∠OPQ = ∠OPR అగును.
కావున, OP అనేది ∠QPR యొక్క కోణ సమద్విఖండన రేఖ అగును. దీని నుండి వృత్త కేంద్రము స్పర్శరేఖల మధ్య ఏర్పడిన కోణం యొక్క సమద్విఖండన రేఖపై వుండునని చెప్పవచ్చును.

ప్రశ్న 2.
రెండు ఏకకేంద్ర వృత్తాలలో బాహ్యవృత్తము యొక్క జ్యా, అంతర వృత్తము యొక్క స్పర్శ బిందువు వద్ద సమద్విఖండన చేయబడును. ఇది ఏ విధముగా సత్యము అగునో చూద్దాం . . .. AS, (పేజీ నెం. 233)
సాధన.
నిరూపణ : O కేంద్రముగా గల రెండు వృత్తాలు C₁ మరియు C₂ అని ఇవ్వబడినవి. C₁ వృత్తము యొక్క జ్యా AB ను చిన్న వృత్తము C₂ ను P వద్ద తాకింది.
(పటం చూడండి) మనము AP = PB అగునని నిరూపించాలి.

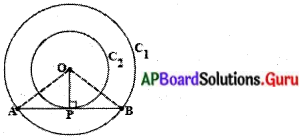
O, P ల ను కలపండి.
C₂ వృత్తానికి AB స్పర్శరేఖ మరియు OP వ్యాసార్ధము . కావున సిద్ధాంతము 1 ప్రకారము
OP ⊥ AB అగును. ఇప్పుడు ∆OAP మరియు ∆OBP లు సర్వసమానాలు. దీని నుండి AP = PB అయినది.
OP అనేది కేంద్రం నుండి గీయబడిన లంబము కావున అది AB జ్యాను సమద్విఖండన చేస్తుంది.

ప్రశ్న 3.
‘O’ కేంద్రముగా గల వృత్తానికి బాహ్యబిందువు A నుండి గీయబడిన స్పర్శరేఖలు AP మరియు AQ అయిన ∠PAQ = 2 ∠OPQ = 2 ∠OQP అగును. దీనిని నిరూపించగలవా ? (పేజీ నెం. 233)
సాధన.

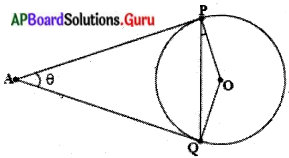
నిరూపణ : O కేంద్రముగా గల వృత్తానికి బాహ్యబిందువు, A నుండి రెండు స్పర్శరేఖలు AP మరియు AQ లు గీయబడ్డాయి. ఇందులో P, Q లు స్పర్శబిందువులు (పటం చూడండి.)
మనము ∠PAQ = ∠OPQ అని నిరూపించాలి.
∠PAQ = θ అయిన ఇప్పుడు సిద్ధాంతము ప్రకారము AP = AQ అగును.
కావున ∆APQ ఒక సమద్విబాహు త్రిభుజము అగును.
అందుచే, ∠APQ + ∠AQP + ∠PAQ = 180° (మూడు కోణాల మొత్తము).
∠APQ = ∠AQP = \(\frac{1}{2}\) (180° – θ) = 90° – \(\frac{1}{2}\) θ
ఇదే విధంగా, సిద్ధాంతము 1 ప్రకారము ∠OPQ = 90°
కావున, ∠OPQ = ∠OPA – ∠APQ
= 90° – [90 – \(\frac{1}{2}\)θ] = \(\frac{1}{2}\) θ = ∠PAQ
దీని నుండి ∠PAQ = ∠OPQ = 2∠OQP అగును.

ప్రశ్న 4.
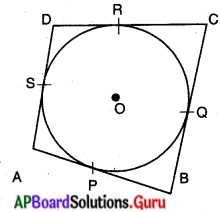
ABCD చతుర్భుజంలోని అన్ని భుజాలను తాకే విధంగా ఒక వృత్తం అంతర్లిఖించబడిన. అది P, Q, R, S బిందువుల వద్ద AB + CD = BC + DA అగును.

సాధన.
నిరూపణ : పటంలో చూపిన విధముగా ABCD భుజాలు AB, BC, CD మరియు DA లను వృత్తము P, Q, R, S బిందువుల వద్ద వరుసగా స్పర్శించింది.
సిద్ధాంతము’ 2 ప్రకారము, బాహ్యబిందువు నుండి వృత్తం పైకి గీయబడిన స్పర్శరేఖల పొడవులు సమానము కావున
AP = AS
BP = BQ
DR = DS మరియు
CR = CQ
వీటిని కలుపగా, మనకు
AP + BP + DR + CR = AS + BQ + DS + CQ
లేదా (AP + PB) + (CR + DR) = (BQ + QC) + (DS + SA)
లేదా AB + CD = BC + DA

ఇవి చేయండి:

ప్రశ్న 1.
శంకర్ రూపొందించిన మరికొన్ని పటాలు ఇవ్వబడ్డాయి.

ఈ పటాల ఆకారాలను ఏవిధంగా విభజిస్తే వీటి వైశాల్యాలు సులభముగా కనుగొనగలము ? మీరు ఇటువంటి మరికొన్ని పటాలను రూపొందించి, విభిన్న పటాలుగా విభజించండి. (పేజీ నెం. 237).
సాధన.
– రెండు దీర్ఘచతురస్రాలు

– ఒక దీర్ఘచతురస్రం మరియు వృత్తం

– ఒక శంఖువు మరియు వృత్తఖండం

– ఒక దీ|| చ|| మరియు రెండు అర్ధవృత్తాలు

విభిన్న ఆకారాల పటాలు –

– శంఖువు మరియు వృత్త ఖండం

– దీ||చ|| మరియు వృత్త ఖండం

– ఒక చతురస్రం మరియు 4 వృత్తఖండాలు.

ప్రశ్న 2.
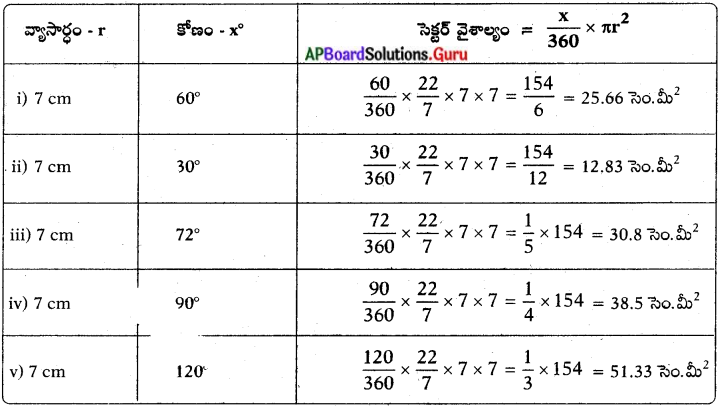
వృత్త వ్యాసార్ధము 7 సెం.మీ మరియు దిగువ సెక్టరు కోణాలకు తగినట్లు సెక్టరు వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
(i) 60°
(ii) 30°
(iii) 72°
(iv) 90°
(v) 120°

సాధన.

ప్రశ్న 3.
ఒక గడియారంలో నిమిషాల ముల్లు పొడవు 14 సెం.మీ. 10 నిమిషాలలో ఈ ముల్లుచే ఏర్పడే ప్రదేశ వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
సాధన.
నిముషాల ముల్లు 191 చేయు కోణం = \(\frac{360^{\circ}}{60}\) = 6°
∴ 10ని||లో నిముషాల ముల్లు చేయు కోణం
= 10 × 6 = 60°
∴ వృత్త వ్యాసార్ధం = నిముషాల ముల్లు పొడవు = r = 14 సెం.మీ.
కోణం = x = 60°
∴ సెక్టార్ వైశాల్యం

= \(\frac{x}{360} \times \pi r^{2}\)
= \(\frac{60}{360} \times \frac{22}{7}\) × 14 × 14
= \(\frac{616}{6}\) = 102.66 సెం.మీ².

ప్రయత్నించండి:

ప్రశ్న 1.
అల్ప వృత్త ఖండ వైశాల్యమును ఉపయోగించి అధిక వృత్తఖండ వైశాల్యమును ఏవిధముగా కనుగొంటావు? (పేజీ నెం. 239)
సాధన.

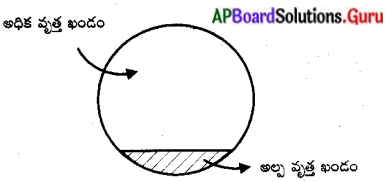
అధిక వృత్తఖండ వైశాల్యం = వృత్త వైశాల్యం – అల్ప వృత్త ఖండ వైశాల్యం.

ఉదాహరణలు:

ప్రశ్న 1.
వృత్త వ్యాసార్ధము 5 సెం.మీ మరియు రెండు స్పర్శరేఖల మధ్యకోణము 60° అయిన ఆ వృత్తానికి స్పర్శరేఖలను గీయండి. (పేజీ.నెం.235)
సాధన.
వృత్తం గీచి దానికి రెండు స్పర్శరేఖలను గీయుటను మనం పరిశీలిద్దాము. మనకు వృత్త వ్యాసార్ధము మరియు రెండు స్పర్శరేఖల మధ్య కోణము ఇవ్వబడింది. వృత్తకేంద్రం నుండి బాహ్యబిందువునకు గల దూరము గాని, స్పర్శరేఖల పొడవులుగాని మనకు తెలియవు. కాని మనకు స్పర్శరేఖల మధ్యకోణము మాత్రమే తెలుసు. దీని నుపయోగించి బాహ్యబిందువు నుండి కేంద్రానికి గల దూరాన్ని కనుగొంటే, మనము స్పర్శరేఖలను గీయవచ్చును.

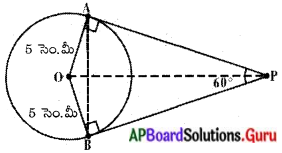
దీనిని ప్రారంభించడానికి ముందు 5 సెం.మీ వ్యాసార్ధము గల వృత్తాన్ని పరిశీలిద్దాము.
బాహ్యబిందువు ‘P’ నుండి PA మరియు PB లు అనేవి వృత్తానికి గీయబడిన స్పర్శరేఖలు మరియు వీటి మధ్య కోణము 60°.
దీనిలో ∠APB = 60°. OP ని కలుపండి. OP అనేది ∠APB కి సమద్విఖండన రేఖ.
కావున ∠OPA = ∠OPB = \(\frac{60^{\circ}}{2}\) = 30
[∵ ∆OAP = ∆OBP]
ఇప్పుడు ∆OAP లో Sin 30° = ఎదుటి భుజము / కర్ణము
= \(\frac{\mathrm{OA}}{\mathrm{OP}}\)
\(\frac{1}{2}=\frac{5}{\mathrm{OP}}\) (త్రికోణమితి నిష్పత్తుల నుండి)
⇒ OP = 10 సెం.మీ.

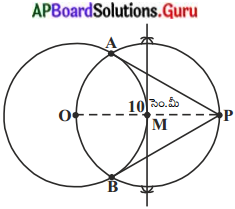
మనం ఇప్పుడు ‘O’ కేంద్రముగా 5 సెం.మీ వ్యాసార్ధంతో వృత్తము గీద్దాము. కేంద్రం నుండి 10 సెం.మీ దూరంలో ‘P’ అనే బిందువును గుర్తిద్దాము. OP ని కలిపి నిర్మాణము పై పటములో చూపిన విధముగా పూర్తి చేద్దాము.
PA మరియు PB అనేవి వృత్తానికి గీయబడిన ఒక – జత స్పర్శరేఖలు ఏర్పడతాయి.

ప్రశ్న 2.
పటములో వృత్త వ్యాసార్ధము 21 సెం.మీ. మరియు ∠AOB = 120° అయిన వృత్తఖండము AYB వైశాల్యము కనుగొనుము. (పేజీ నెం. 239)
(π = \(\frac{22}{7}\) మరియు √3 = 1.732 గా తీసుకోండి).
సాధన.
AYB వృత్తఖండ వైశాల్యము = OAYB సెక్టరు వైశాల్యము – ∆DAB వైశాల్యము
ఇప్పుడు OAYB సెక్టరు వైశాల్యము = \(\) × 21 × 21 చ.సెం.మీ
= 462 చ. సెం.మీ. …………. (1)

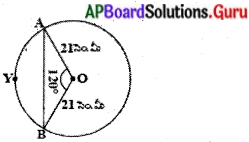
∆OAB వైశాల్యము కనుగొనుటకు పటములో చూపిన విధముగా OM ⊥ AB ను గీయాలి.
OA = OB కావున లం.క.భు. సర్వసమాన నియమము ప్రకారము ∆AMO = ∆BMO అగును.
కావున, AB మధ్యబిందువు M అగును మరియు ∠AOM = ∠BOM = \(\frac{1}{2}\) × 120° = 60°.
ఇప్పుడు OM = x సెం.మీ అనుకొనిన
∆OMA నుండి, OM = cos 60° లేదా,
\(\frac{x}{21}=\frac{1}{2}\) (∵ cos 60° = \(\frac{1}{2}\)) లేదా,
x = \(\frac{21}{2}\)
కావున, OM = \(\frac{21}{2}\) సెం.మీ

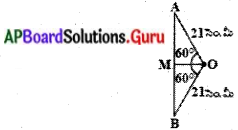
అలాగే, \(\frac{\text { AM }}{\text { OA }}\) = sin 60
⇒ \(\frac{\text { AM }}{21}=\frac{\sqrt{3}}{2}\) (sin 60° = \(\frac{\sqrt{3}}{2}\))
కావున, AM = 21\(\frac{\sqrt{3}}{2}\) సెం.మీ.
అందువలన AB = 2AM = \(\frac{2 \times 21 \sqrt{3}}{2}\) సెం.మీ. = 21√3 సెం.మీ.
దీని నుండి ∆OAB వైశాల్యము = \(\frac{1}{2}\) × AB × OM
= \(\frac{1}{2}\) × 21√3 × \(\frac{21}{2}\) చ.సెం.మీ²
= \(\frac{441}{4}\)√3 చ.సెం.మీ ……… (2)
ఈ విధంగా (1), (2) లను బట్టి AYB వృత్తఖండం వైశాల్యము
= (462 – \(\frac{441}{4}\)√3) చ.సెం.మీ²
= \(\frac{21}{4}\) (88 – 21√3) చ.సెం.మీ²
= 271.047 చ.సెం.మీ².

ప్రశ్న 3.
పటములో 0 కేంద్రముగా వృత్తములో PQ = 24 సెం.మీ. PR = 7 సెం.మీ మరియు వ్యాసము QR అని ఇవ్వబడింది. షేడ్ చేయబడిన వృత్తఖండము వైశాల్యము కనుగొనుము. (π = \(\frac{22}{7}\) తీసుకోండి). (పేజీ నెం. 241)
సాధన.
షేడ్ చేయబడిన వృత్తఖండం వైశాల్యము = OQPR సెక్టరు వైశాల్యము – PQR త్రిభుజ వైశాల్యము.
QR వ్యాసము కావున, ∠QPR= 90° (అర్ధవృత్తములో కోణము) పైథాగరస్ సిద్ధాంతమును ఉపయోగించి,
∆QPR,
QR² = PQ² + PR²
= 24² + 7²
= 576 + 49 = 625
QR = √625 = 25 సెం.మీ

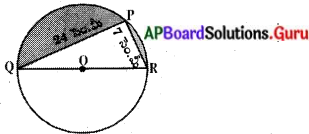
దీని నుండి వృత్త వ్యాసార్ధము = \(\frac{1}{2}\) QR
= \(\frac{1}{2}\) (25) = \(\frac{25}{2}\) సెం.మీ
ఇపుడు, OQPR అర్ధవృత్త వైశాల్యము = \(\frac{1}{2}\) πr²
= \(\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}\)
= 327.38 చ.సెం.మీ ………………..(1)
QPR లంబకోణ త్రిభుజ వైశాల్యము = \(\frac{1}{2}\) × PR × PQ
= \(\frac{1}{2}\) × 7 × 24
= 84 చ.సెం.మీ …………………..(2)
(1), (2) లను బట్టి, షేడ్ చేయబడిన వృత్తఖండము వైశాల్యము = 327.38 – 84
= 243.38 చ.సెం.మీ².

ప్రశ్న 4.
పటములో చూపిన విధముగా ఒక గుండ్రని ఉపరితలము గల బల్లపై ఆరు సమాన ఆకృతులు కలవు. బల్లపై తలము యొక్క వ్యాసార్ధము 14 సెం.మీ అయిన చ.మీ ₹ 5 చొప్పున బల్లపై గల ఆకృతులకు రంగు వేయడానికి ఎంత ఖర్చు అవుతుంది ? (√3 = 1.732 తీసుకోండి) (పేజీ నెం. 241)
సాధన.
వృత్తములో అంతర్లిఖించబడిన క్రమషడ్భుజి యొక్క భుజము వృత్త వ్యాసార్ధానికి సమానమని మనకు తెలుసు.
∴ క్రమషడ్భుజి యొక్క ఒక్కొక్క భుజము = 14 సెం.మీ.

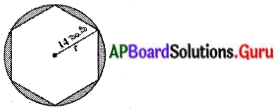
అందువలన, ఆకృతి చేయబడిన ఆరు వృత్త ఖండాల వైశాల్యము = వృత్త వైశాల్యము – క్రమషడ్భుజి వైశాల్యము ఇపుడు, వృత్త వైశాల్యము = Tr
= \(\frac{22}{7}\) × 14 × 14 = 616 చ.సెం.మీ² ………………. (1)
క్రమషడ్భుజి వైశాల్యము
= 6 × \(\frac{\sqrt{3}}{4}\) a²
= 6 × \(\frac{\sqrt{3}}{4}\) × 14 × 14
= 509.2 చ.సెం.మీ² ……………… (2)
(1), (2) లను బట్టి ఆరు ఆకృతుల
మొత్తం వైశాల్యం = 616 – 509.21 = 106.79 చ.సెం.మీ²
దీని నుండి, చ.మీ ₹ 5 చొప్పున ఆరు ఆకృతులకు రంగు వేయుటకు అయ్యే ఖర్చు = ₹ 106.79 × 5 = ₹ 533.95