SCERT AP 10th Class Maths Textbook Solutions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Optional Exercise Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు Optional Exercise
ప్రశ్న 1.
బాహ్యబిందువు నుండి వృత్తము పైకి గీయబడిన రెండు స్పర్శరేఖల మధ్య కోణము మరియు రెండు స్పర్శ బిందువులను కేంద్రంతో కలుపుతూ గీయబడిన రేఖా ఖండాలు ఏర్పరచిన కోణానికి సంపూరకమని నిరూపించండి.
సాధన.
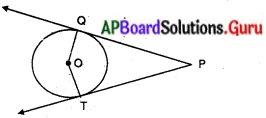
దత్తాంశం : ‘0’ కేంద్రంగా గల వృత్తమునకు PQ, PTలు బాహ్య బిందువు P నుండి వృత్తానికి గీయబడిన స్పర్శరేఖలు.
సారాంశం : ∠P + ∠QOT = 180°
ఉపపత్తి : OQ ⊥ PQ
[∵ వ్యాసార్ధం, స్పర్శరేఖకు లంబంగా ఉండును]
అదే విధంగా OT ⊥ PT
∴ ∠OQT + ∠OTP
= 90° + 90° = 180°
PQOT చతుర్భుజంలో ∠OTP + ∠TPQ + ∠PQO + ∠QOT = 360°
⇒ 180° + ∠P + ∠QOT = 360°
⇒ ∠P + ∠QOT = 180°
∴ సిద్ధాంతం నిరూపించబడినది.
![]()
ప్రశ్న 2.
5సెం.మీ వ్యాసార్ధముగా గల వృత్తములో PQ జ్యా పొడవు 8 సెం.మీ. P మరియు Q గుండా గీయబడిన స్పర్శరేఖలు | వద్ద ఖండించుకున్నాయి. (పటము చూడండి) అయిన TP పొడవును కనుగొనండి.
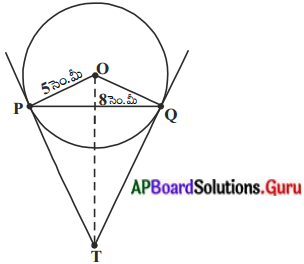
సాధన.
ఇచ్చినవి : ‘0’ కేంద్రంగా గల వృత్త వ్యాసార్ధం (r) = OP = 5 సెం.మీ.
PQ జ్యా పొడవు = 8 సెం.మీ.;
TP పొడవు = ?
∆PTR, ∆QTRల నుండి PT = QT (స్పర్శరేఖల పొడవులు సమానాలు)
∠PTR = ∠QTR [:: ∆POT = ∆POT]
TR = TR (ఉమ్మడి భుజం] .
PR = QR
∆OPR నుండి ∠PRO = 90°
[∵ వృత్త కేంద్రం నుండి గీచిన జ్యా పై రేఖ దానిని లంబ సమద్విఖండన చేయును]
∴ OR2 = OP2 – PR2
= 52 – 42 = 9
∴ OR = 3సెం.మీ.
∆OPT నుండి, ∠POT + ∠PTO = 90° ……………. (1)
⇒ ∠POR + ∠PTR = 90° ………………(2)
(1), (2) ల నుండి ∠OPR = ∠PTR అగును.
∴ ∆ORP ~ ∆PRT
∴ \(\frac{\mathrm{TP}}{\mathrm{PO}}=\frac{\mathrm{PR}}{\mathrm{RO}}\)
⇒ \(\frac{\mathrm{TP}}{5}=\frac{4}{3}\)
⇒ TP = \(\frac{4 \times 5}{3}=\frac{20}{3}\) సెం.మీ.
∴ TP = 6.66 సెం.మీ.
![]()
ప్రశ్న 3.
ఒక చతుర్భుజములో వృత్తము దాని నాలుగు భుజాలను తాకుతూ అంతర్లిఖించబడి వున్నచో ఆ చతుర్భుజము ఎదుటి భుజాలు వృత్త కేంద్రము వద్ద చేయు కోణాలు సంపూరకాలని నిరూపించండి.
సాధన.
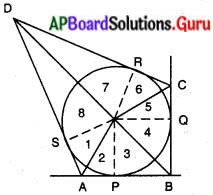
దత్తాంశం : ‘O’ కేంద్రంగా గల వృత్తం ABCD చతుర్భుజాన్ని AB, BC, CD, DA భుజాలపై వరుసగా P, Q, R, S వద్ద తాకుచున్నది.
సారాంశం : ∠AOB + ∠COD = 180°
∠AOD + ∠BOC = 180°
నిర్మాణం : (O, P), (O, Q), (O, R) (O, S) లను కలుపుము.
ఉపపత్తి : బాహ్య బిందువు నుండి వృత్తం పైకి గీచిన స్పర్శరేఖలు కేంద్రం వద్ద సమాన కోణాలను చేస్తాయి.
అనగా ∠1 = ∠2; ∠3 = ∠4; ∠5 = ∠6; ∠7 = ∠8
∠1 + ∠2 + ∠3 + ∠4 + ∠5 + ∠6 + ∠7 + ∠8 = 360°
2 (∠2 + ∠3 + ∠6 + ∠7) = 360°
(లేదా) (∠2 + ∠3) + ∠6 + ∠7 = 180°
అదే విధంగా 2 (∠1 + ∠8 + ∠4 + ∠5) = 360°
⇒ (∠1 + ∠8) + (∠4 + ∠5) = 180°
కానీ, ∠AOB + ∠COD = 180° మరియు ∠AOD + ∠BOC = 180°
[∵ ∠2 + ∠3 = ∠AOB; ∠6 + ∠7 = ∠COD
∠1 + ∠8 = ∠AOD
∠4 + ∠5 = ∠BOC పటం నుండి]
![]()
ప్రశ్న 4.
8 సెం.మీ పొడవు గల AB రేఖాఖండాన్ని గీయండి. A కేంద్రముగా 4 సెం.మీ వ్యాసార్ధముతో ఒక వృత్తము, B కేంద్రముగా 3 సెం.మీ వ్యాసార్ధముతో మరొక వృత్తము గీయండి. ఒక వృత్త కేంద్రము నుండి మరొక వృత్తానికి స్పర్శరేఖలను గీయండి.
సాధన.
చిత్తు పటం :
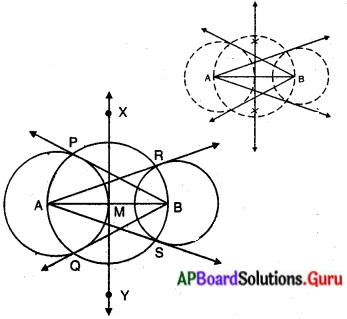
నిర్మాణ క్రమం :
(1) 8 సెం.మీల వ్యాసార్ధంచే AB అను రేఖాఖండాన్ని నిర్మించుము.
(2) A మరియు B కేంద్రాలుగా వరుసగా 4 సెం.మీ, 5 సెం.మీల వ్యాసార్థంచే రెండు వృత్తాలు నిర్మించుము.
(3) ABకి XY అను లంబసమద్వి ఖండన రేఖను గీయుము. అది AB ను M వద్ద ఖండించినది.
(4) M కేంద్రంగా MA లేదా MB వ్యాసార్థంచే ఒక వృత్తాన్ని గీయగా అది A కేంద్రంగా గల వృత్తాన్ని P, Q బిందువుల వద్ద B కేంద్రంగా గల వృత్తాన్ని R, S ల వద్ద ఖండించును.
(5) (B, P), (B, Q) మరియు (A, R), (A, S) లను కలుపుము.
∴ కావలసిన నిర్మాణం ఏర్పడినది.
![]()
ప్రశ్న 5.
ABC లంబకోణ త్రిభుజములో AB = 6 సెం.మీ, BC = 8 సెం.మీ మరియు ∠B = 90°. B శీర్షం నుండి AC పైకి గీయబడిన లంబము BD మరియు B, C, D బిందువుల గుండా వృత్తము గీయబడింది. A నుండి ఈ వృత్తము పైకి స్పర్శరేఖలను గీయండి.
సాధన.
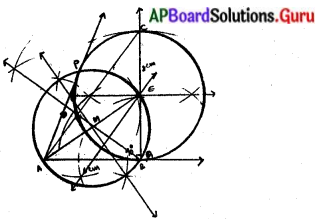
నిర్మాణ క్రమం :
(1) AB = 6 సెం.మీ., LB = 90°, BC = 8 సెం.మీ.ల కొలతలతో AABC ను నిర్మించుము.
(2) AC పైకి B నుండి BD అను ఒక లంబాన్ని గీయుము.
(3) ABCDకి ఒక పరివృత్తాన్ని గీయుము. దాని కేంద్రం ‘E’ గా గుర్తించుము.
(4) A, Eలను కలుపుము. AE పై లంబ సమద్విఖండన రేఖ XY ను నిర్మించుము. అది AE ని M వద్ద ఖండించును.
(5) M కేంద్రంగా MA లేదా ME వ్యాసార్ధాలచే ఒక వృత్తాన్ని నిర్మించగా అది ABCD యొక్క పరివృత్తాన్ని P మరియు B వద్ద ఖండించినది.
∴ కావలసిన నిర్మాణం ఏర్పడినది.
![]()
ప్రశ్న 6.
A, B కేంద్రాలుగా గల రెండు వృత్తాలు C వద్ద స్పర్శించుకున్నాయి. AC = 8 సెం.మీ. మరియు AB = 3 సెం.మీ అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యము కనుగొనుము.
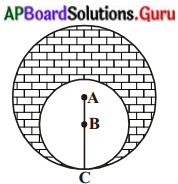
సాధన.
A, B కేంద్రాలుగా గల రెండు వృత్తాల వ్యాసార్థాలు వరుసగా r1 = 8 సెం.మీ. r2 = 5 సెం.మీ.
[∵ AC = 8 సెం.మీ, AB = 3 సెం.మీ. ⇒ BC = 8 – 3 = 5 సెం.మీ]
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = పెద్ద వృత్త వైశాల్యం – చిన్న వృత్త వైశాల్యం .
= πr12 – πr12
= π (r12 – r12)
= \(\frac{22}{7}\) (82 – 52)
= \(\frac{22}{7}\) × (64 – 25)
= \(\frac{22}{7}\) × 39
= 204.28 సెం.మీ2.
![]()
ప్రశ్న 7.
AB = 14 సెం.మీ. మరియు BC = 1 సెం.మీ కొలతలు ABCD దీర్ఘచతురస్రము గీయబడింది. DC, BC మరియు AD వ్యాసాలుగా గల మూడు అర్ధవృత్తాలు పటములో చూపినట్లుగా గీయబడినవి. అయిన షేడ్ చేసిన ప్రదేశ వైశాల్యమును కనుగొనుము.
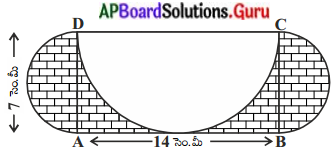
సాధన.
మొత్తం ఇచ్చిన పట వైశాల్యం = (2 × AD వ్యాసంగా గల అర్ధవృత్త వైశాల్యం + దీ||చ|| ABCD వైశాల్యం)
= 2 × × πr2 + (l × b)
= 2 × \(\frac{180}{360^{\circ}} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\) + (14 × 7)
= \(\frac{77}{2}\) + 98 = \(\frac{273}{2}\) సెం.మీ.
షేడ్ చేయని ప్రాంత వైశాల్యం = \(\frac{1}{2} \times \frac{22}{7} \times \frac{14}{2} \times \frac{14}{2}\)
= 77 సెం.మీ2
షేడ్ చేయబడిన ప్రాంత వైశాల్యం = మొత్తం పట వైశాల్యం – షేడ్ చేయబడని ప్రాంత వైశాల్యం
= \(\frac{273}{2}\) – 77 = \(\frac{273-154}{2}\)
= \(\frac{119}{2}\) = 59.5 సెం.మీ2