AP Board 5th Class Maths Solutions 5th Lesson గుణిజాలు – కారణాంకాలు

Andhra Pradesh AP Board 5th Class Maths Solutions 5th Lesson గుణిజాలు – కారణాంకాలు Textbook Exercise Questions and Answers.

AP State Syllabus 5th Class Maths Solutions Chapter 5 గుణిజాలు – కారణాంకాలు

కింది ఇవ్వబడిన సంఖ్యలలో ఏవి 2చే నిశ్శేషంగా భాగించబడతాయో భాగహారం చేసి చూడండి. ఏవి 2చే భాగించబడవో పరిశీలించండి.

2410, 1282, 3184, 6728, 5633, 1789, 5466, 1787

పై వానిలో ఏఏ సంఖ్యలు 2చే నిశ్శేషంగా భాగించబడతాయి?
జవాబు.
2410, 1282, 3784, 6728, 5466

2చే భాగించబడిన సంఖ్యల ఒకట్ల స్థానాన్ని పరిశీలించండి.
జవాబు.
0, 2, 4, 6, 8

(ఆ సంఖ్యలన్ని సరి సంఖ్యలేనా? అవును /కాదు)
జవాబు.
అవును. అన్నీ సరి సంఖ్యలే
కావున ఒక సంఖ్య 2 చే నిశ్శేషంగా భాగించబడాలంటే ఆ సంఖ్య ఒకట్ల స్థానంలో 0/2/ 4/6/8 సంఖ్యలు ఉండాలి.

ఇవి చేయండి: (TextBook Page No. 37)

ప్రశ్న 1.
2చే భాగించబడు సంఖ్యలకు ‘O’ చుట్టండి.
2469 7435 8496 7630 4301 8023 4678 2030 22247 1972 6120 1524
జవాబు.
8496, 7630, 4678, 2030, 7972, 6120, 1524

ప్రశ్న 2.
2చే భాగించబడు నాలుగంకెల సంఖ్యలు ఏవైనా అయిదింటిని రాయండి.
జవాబు.
25680, 45,622, 78,964, 87,766, మరియు 97,678.

అభ్యాసం 1:

ప్రశ్న 1.
2చే భాగించబడు సంఖ్యలను గుర్తించండి. భాగించబడకపోవడానికి కారణాలు వ్రాయండి.
అ) 3458
ఆ) 56745
ఇ) 3850
ఉ) 6736
ఉ) 6733
ఊ) 3394
జవాబు.
3458, 3850, 6736 మరియు 3394 లు
2చే నిశ్శేషంగా భాగించబడును. మిగిలి సంఖ్యలు చే. భాగించబడవు.
కారణం :
ఈ సంఖ్యలు ఒకట్ల స్థానంలో 3 మరియు 5 కలవు.

ప్రశ్న 2.
5 మరియు 10చే భాగించబడు సంఖ్యలను కనుక్కోండి. భాగించబడకపోవడానికి కారణాలు వ్రాయండి.
అ) 3568
ఆ) 3540
ఇ) 6585
ఈ) 7550
ఉ) 4235
ఊ) 7200
ఋ) 7865
ౠ) 5880
ఎ) 7885
ఏ) 4440
ఐ) 8198
ఒ) 8645
జవాబు.
ఆ, ఈ, ఊ, ఋ మరియు ఐలు 5 మరియు 10 లచే భాగించబడు సంఖ్యలు అగును.
కారణం :
ఒకట్ల స్థానములో ‘0’ ఉన్న సంఖ్యలన్నీ 10చే నిశ్శేషంగా భాగించబడతాయి.

ప్రశ్న 3.
కింది ఉన్న సంఖ్యలలో ఖాళీలను ఏ అంకెలతో పూరిస్తే అవి 5చే నిశ్శేషంగా భాగించబడతాయి.
అ) 786____
జవాబు.
786___(0/5)

ఆ) 560____
జవాబు.
560___(0/5)

ఇ) 785____
జవాబు.
785___(0/5)

ఈ) 555____
జవాబు.
555___(0/5)

ఉ) 586____
జవాబు.
586___(0/5)

ఊ) 786____
జవాబు.
786___(0/5)

ఋ) 584____
జవాబు.
584___(0/5)

ౠ) 100____
జవాబు.
100___(0/5)

ప్రశ్న 4.
2 మరియు 5లచే నిశ్శేషంగా భాగించబడు ఏవేనా 5 సంఖ్యలు రాయండి.
జవాబు.
2540, 62570, 250, 367280 మరియు 764520.

ప్రశ్న 5.
2, 5 మరియు 10లచే విశ్శేషంగా భాగించబడు ఏవేవా 5 సంఖ్యలు రాయండి.
జవాబు.
86540, 19980, 89960, 45570 మరియు 76540.

ఇవి చేయండి: (TextBook Page No.43)

ప్రశ్న 1.
3, 9 లచే భాగించబడు సంఖ్యలకు చుట్టండి, కారణం తెలపండి.
అ) 108
ఆ) 116
ఇ) 117
ఈ) 127
ఉ) 132
ఊ) 822
ఋ) 435
ౠ) 783
ఎ) 1107
ఎ) 5535
ఏ) 2343
ఐ) 4563
జవాబు.
108, 117, 132, 822, 1107, 4563
కారణం : ఇచ్చిన సంఖ్యల అంకమూలము 9 అయిన అది 3 మరియు 9 లచే నిశ్శేషంగా భాగించబడును.

ప్రశ్న 2.
3, 9 లచే భాగించబడు ఏవైనా 5 సంఖ్యలు రాయండి.
జవాబు.
1350, 1476, 3420, 1539 మరియు 1629.

ఇవి చేయండి: (TextBook Page No.45)

ప్రశ్న 1.
4 చే భాగించబడు సంఖ్యలకు ‘O’ చుట్టండి. భాగింపబడని సంఖ్యలకు కారణం తెలపండి.
అ) 2436
ఆ) 3840
ఇ) 1235
ఈ) 3636
ఉ) 6850
ఊ) 5644
ఋ) 8888
ఋ) 6430
జవాబు.
అ, ఆ, ఈ, ఊ మరియు ఋ లు 4చే నిశ్శేషంగా భాగించబడును. మిగిలిన సంఖ్యలు యొక్క చివరి రెండు స్థానాలలోని అంకెలతో ఏర్పడు సంఖ్య 4చే భాగించబడితే, ఆ సంఖ్య 4చే భాగించబడుతుంది.

ప్రశ్న 2.
క్రింది సంఖ్యలు 4చే భాగించబడాలంటే సరియైన అంకెలతో ఖాళీలను నింపండి.
అ) 323____
జవాబు.
323___(2/6)

ఆ) 304____
జవాబు.
304___(0)

a) 58___6
జవాబు.
58___6 (1/3)

ఈ) 53________
జవాబు.
53____ (04/08/12/16/20/24/28/36/40)

ఉ) 65______
జవాబు.
65_____ (04/08/12/16/20/24/28/36/40)

ఇవి చేయండి: (TextBook Page No.49)

ప్రశ్న 1.
కింది ఇవ్వబడిన సంఖ్యలు 6చే భాగించబడతాయో లేదో పరీక్షించండి.
1) 210
2) 162
3) 625
4) 120
5) 156
జవాబు.
210, 162, 120 మరియు 156, ద్వారా విభజించబడతాయి.

ప్రశ్న 2.
కింది ఇవ్వబడిన సంఖ్యలు 6చే భాగించబడేలా అంకెల స్థానాలను సరి చేయండి.
1) 543
2) 231
3) 5463
4) 1002
5) 4815
జవాబు.

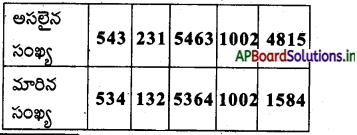
ఇవి చేయండి: (TextBook Page No.47)

ప్రశ్న 1.
కింద ఇవ్వబడిన సంఖ్యలు 8తో భాగించబడతాయా, కనుక్కోండి?
అ) 2456
ఆ) 3971
ఇ) 824
ఈ) 923
ఉ) 2780
ఊ) 93624
ఋ) 76104
జవాబు.
అ)2456లోని, 456 ను 83 భాగించబడుచున్నది. కనుక కాబట్టి, 2456కూడా 8చే భాగించబడుతుంది.
ఆ) 3971లోని చివరి మూడంకెలు 971, 8చే భాగించబడదు. కనుక 3971, 8 చే భాగించబడదు.
ఇ) 824, 8చే భాగించబడుచున్నది.
ఈ) 923, 8 చే భాగంచబడదు.
ఉ) 2780 లోని చివరి మూడంకెలు 780, 8చే భాగించబడదు. కనుక 2780, 8చే నిశ్శేషంగా భాగించబడదు.
ఊ) 93624లోని చివరి మూడంకెలు 624, 8చే భాగించబడును. కనుక 93624, 8చే నిశ్శేషంగా భాగించబడును.
ఋ) 76104లోని చివరి మూడంకెలు 104, 8చే భాగంచబడును కనుక 76104, 8చే భాగంచబడును.

అభ్యాసం 2:

ప్రశ్న 1.
2 భాజనీయతా సూత్రం ఉపయోగించి, 2చే భాగించబడు సంఖ్యలకు చుట్టండి.
3624 3549 7864 8420 8500 8646 5007 7788
జవాబు.
3624
7864
8420
8500
8646
7788

ప్రశ్న 2.
6 చే విశ్శేషంగా భాగించబడు సంఖ్యలను గుర్తించండి.
1276 43218 71218 71826 4734 3743
జవాబు.
i) ఇచ్చిన సంఖ్య = 1276
1276లో ఒకట్ల స్థానంలో 6 అను సరి సంఖ్య కలదు కనుక 1276, 2 చే నిశ్శేషంగా భాగించబడును.
1276 అంకమూలం = 1 + 2 + 7 + 6 = 16
16, 3చే భాగంచబడదు కనుక 1276, 3చే నిశ్శేషంగా భాగించబడదు.
∴ 1276, 6చే నిశ్శేషంగా భాగించబడదు.

ii) ఇచ్చిన సంఖ్య = 43218
43218లో ఒకట్ల స్థానంలో 8 అను సరి సంఖ్య కలదు.
కనుక 43218, ‘2’ చే నిశ్శేషంగా భాగించబడును.
43218 అంకమూలం = 4 + 3 + 2 + 1 + 8 = 18
18, 3చే భాగంచబడును.
కనుక 43218, 6చే నిశ్శేషంగా భాగించబడును.

iii) ఇచ్చిన సంఖ్య = 71218
71218లో ఒకట్ల స్థానంలో ‘8’ అను సరి సంఖ్య కలదు.
కనుక 71218, ‘2’ చే నిశ్శేషంగా భాగించబడును.
71218 అంకమూలం = 7 + 1 + 2 + 1 + 8 = 19
∴ 19, 3చే నిశ్శేషంగా భాగించబడదు.
కనుక 71218, 6చే నిశ్శేషంగా భాగించబడదు.

iv) ఇచ్చివ సంఖ్య = 71826
71826లో ఒకట్ల స్థానంలో ‘6’ అను సరి సంఖ్య కలదు.
కనుక 71826, ‘2’ చే’ ‘ నిశ్శేషంగా భాగించబడును.
71826 అంకమూలం = 7 + 1 + 8 + 2 + 6 = 24.
∴ 24, 3చే నిశ్శేషంగా భాగించబడును.
కనుక 71826, 6చే నిశ్శేషంగా భాగించబడును.

v) ఇచ్చిన సంఖ్య = 4734
4734లో ఒకట్ల స్థానంలో ‘4’ అను సరి సంఖ్య: కలదు.
కనుక 4734, ‘2’ చే నిశ్శేషంగా భాగించబడును.
4734 అంకమూలం = 4 + 7 + 3 + 4 = 18
∴ 18, 3చే నిశ్శేషంగా భాగించబడును.
కనుక 4734, 6చే నిశ్శేషంగా భాగించబడును.

vi) ఇచ్చిన సంఖ్య = 3743
3743వలో ఒకట్ల స్థానంలో ‘3’ అను బేసి సంఖ్య కలదు.
కనుక 3743, ‘2’ చే . నిశ్శేషంగా భాగించబడదు.
కనుక 3743, 6చే భాగించబడదు.

ప్రశ్న 3.
50 19 అను సంఖ్యను 9చే నిశ్శేషంగా భాగించబడాలంటే లో ఏ సంఖ్య రావాలి.
జవాబు.
ఇచ్చిన సంఖ్య 50 19, 9చే నిశ్శేషంగా భాగించబడుచున్నది కనుక అంకమూలం
5 + 0 + ? + 1 + 9 = 15 + ?
= 15 + 3 = 18
= 1 + 8 = 9
∴ 9, 9చే నిశ్శేషంగా భాగించబడును.
∴ 50 – 19 అను సంఖ్య 9చే నిశ్శేషంగా భాగించబడాలంటే – లో ‘3’ అను సంఖ్య రావాలి.

ప్రశ్న 4.
4 468 అను సంఖ్యను 9చే నిశ్శేషంగా ఆ భాగించబడాలంటే లో ఏ సంఖ్య రావాలి.
జవాబు.
ఇచ్చిన సంఖ్య 4_468, 6చే , నిశ్శేషంగా భాగించబడును కనుక
అంకమూలం = 4 + _ + 4 + 6 + 8
= 22 + 2 = 24
24, 3చే నిశ్శేషంగా భాగించబడును.
కనుక 4 2 468, 6చే నిశ్శేషంగా భాగించబడును.

ప్రశ్న 5.
కింది ఇవ్వబడిన సంఖ్యలు 2 మరియు 10లచే భాగించబడాంటే ఖాళీలలో ఏ అంకె ఉండాలి?
678_, 588_, 388_, 222_, 364_, 786_ , 666_ , 788_ ,
జవాబు.
ఇచ్చిన సంఖ్యలు 10 చే భాగించబడ వలెనన్న వాటి ఒకట్ల స్థానంలో ‘0’ను’ కళా వెండవలెను.
ఆ సంఖ్యలు ‘0’ను కల్గి వున్న ‘2 చే భాగించబడును.
6780 5880 3880 2220 3640.7860 6660 7880

ప్రశ్న 6.
4 మరియు 8లచే భాగించబడు సంఖ్యలను గుర్తించండి.
2104 726352 1800 32256 52248 25608.
జవాబు.
ఇచ్చిన సంఖ్యల యొక్క చివరి రెండు స్థానాలను గమనించగా అవి 04, 52, 00, 56, 48 మరియు 08 లుగా గలవు.
ఈ రెండు స్థానాల అంకెలు ‘4’ యొక్క గుణిజాలు కనుక ఇచ్చి సంఖ్యలు 4చే నిశ్శేషంగా భాగించబడతాయి.

8 చేభాజనీయత :
ఇచ్చిన సంఖ్యల యొక్క చివరి మూడు స్థానాలు వరుసగా 104, 352, 800, 256 మరియు 248లు కలవు. ఈ మూడు స్థానాల ‘అంకెలు ‘8’ యొక్క గుణిజాలు కనుక ఇచ్చిన సంఖ్యలు 8చే నిశ్శేషంగా భాగించబడతాయి.

i) ఇచ్చిన సంఖ్య 2104
ఇచ్చిన సంఖ్య యొక్క, చివరి మూడు స్థానాలు 104 అయిన, 104, 8 చే – భాగించబడును కనుక 2104 కూడా 8చే భాగించబడుతుంది.

ii) ఇచ్చిన సంఖ్య 726352
ఇచ్చిన సంఖ్య యొక్క చివరి మూడు స్థానాలు 352, ఈ 352, 8 చే భాగించబడును కనుక 726352 కూడా 8చే భాగించబడును.

iii) ఇచ్చిన పంఖ్య 1800
ఇచ్చిన సంఖ్య చివరి మూడు స్థానాలు 800, ఈ 800, 8 చే భాగించబడును కనుక 1800 కూడా 8చే భాగించబడును.

iv) ఇచ్చివ సంఖ్య 32256
ఇచ్చిన సంఖ్య చివరి మూడు స్థానాలు 256, ఈ 256, 8 చే భాగించబడును కనుక 32256 కూడా 8చే భాగించబడును.

v) ఇచ్చిన సంఖ్య 52248
ఇచ్చిన సంఖ్య చివరి మూడు స్థానాలు 248, ఈ 248, 8 చే భాగించబడును కనుక 52248 కూడా 8చే భాగించబడుతుంది.

ప్రశ్న 7.
కింది ఇవ్వబడిన సంఖ్యలు 2, 3, 4, 5, 6, 8, 9 మరియు 10లచే భాగించబడునో లేదో చూడండి.
అ) 333
ఆ) 128
ఇ) 225
ఈ) 7535
ఉ) 8289
ఊ) 99483
ఋ) 67704
ౠ) 67713
ఎ) 9410
ఏ) 67722
ఐ) 20704
ఒ) 35932
ఓ) 85446
క) 90990
ఖ) 18540
జవాబు.
ఆ) ఇచ్చివ సంఖ్య 333
333 యొక్క అంకమూలం 3 + 3 + 3 = 9
∴ 9 అను సంఖ్య 3 మరియు 9ల గుణిజము. కనుక 333 అను సంఖ్య. 3 ‘మరియు 9లచే నిశ్శేషంగా భాగించబడును.

ఆ) ఇచ్చిన సంఖ్య 128
ఈ సంఖ్య ఒకట్ల స్థానపు అంకె 8’. ఇది సరిసంఖ్య కనుక 128, 2చే నిశ్శేషంగా భాగించబడును.
ఇచ్చిన సంఖ్య యొక్క చివరి రెండు స్థానాల సంఖ్య 28, 4 యొక్క గుణిజము కనుక 128, 4చే నిశ్శేషంగా భాగించబడును.
128 ÷ 8 = 16, కనుక 128, 8చే భాగించబడును.
∴ 128 అను సంఖ్య 2, 4 మరియు 8చే భాగించబడును.

ఇ) ఇచ్చివ సంఖ్య 225.
ఈ సంఖ్య -ఒకట్ల స్థానంలో ‘5’ అంకే కలదు. కనుక ఇది 5చే నిశ్శేషంగా భాగించబడును.

ఈ) ఇచ్చిన సంఖ్య 7535.
ఈ సంఖ్య ఒకట్ల స్థానంలో ‘5’ అంకె కలదు. కనుక ఇది 5చే నిశ్శేషంగా భాగించబడును.

ఉ) ఇచ్చిన సంఖ్య 8289.
8289 యొక్క అంకమూలం 8 + 2 + 8 + 9 = 27 = 2 + 7 = 9
9, అను సంఖ్య 3 మరియు 9 లచే భాగించబడును. కనుక 8289 కూడా 3 మరియు 9లచే భాగించబడును.

ఊ) ఇచ్చిన సంఖ్య 99483.
99483 యొక్క అంకమూలం 9 + 9 + 4 + 8 + 3 = 33 = 3 + 3 = 6
6 అను సంఖ్య 3 గుణిజము కనుక 99483, 3చే భాగించబడును.

ఋ) ఇచ్చివ సంఖ్య 67704.
ఈ సంఖ్య ఒకట్ల స్థానంలో ‘4’ అంకె గలదు. కనుక ఇచ్చిన సంఖ్య 2చే భాగించబడును.
67704 యొక్క అంకమూలం 6 + 7 + 7 + 0 + 4 = 24 = 2 + 4 = 6
6 అను సంఖ్య 3 యొక్క గుణిజం కనుక 67704, 3చే భాగించబడును. కనుక 67704, 6చే భాగించబడును.
ఇచ్చిన సంఖ్య చివరి రెండు స్థానాల అంకెలు 04 కనుక ఇది 67704, 4చే భాగించబడును.
ఇచ్చిన సంఖ్య చివరి మూడుస్థానాల అంకెలు 704, 704, 8చే భాగించబడును. కనుక 67704, 8చే భాగించబడును.
∴ 67704 సంఖ్య 2, 3, 4, 6 మరియు 8లచే భాగించబడును.

ౠ) ఇచ్చివ సంఖ్య 67713.
ఈ సంఖ్య అంకమూలం 6 + 7 + 7 + 1 + 3 = 24 = 2 + 4 = 6
‘6’, 3చే భాగించబడును కనుక 67713, 3చే భాగించబడును.

ఎ) ఇచ్చిన సంఖ్య 9410. దత్త సంఖ్య చివరి అంకె ‘O’ కనుక 9410,
2చే నిశ్శేషంగా భాగించబడును.

ఏ) ఇచ్చిన సంఖ్య 67722.
దత్త సంఖ్య చివరి అంకె 2′ కనుక 67722, 2చే నిశ్శేషంగా భాగించబడును.
67722 యొక్క అంకమూలం 6 + 7 + 7 + 2 + 2 = 24 = 2 + 4 = 6 ఇది 3చే భాగించబడును.
67722 అను సంఖ్య 2,3 మరియు 6 లచే భాగించబడును.

ఐ) ఇచ్చిన సంఖ్య 20704.
దత్త సంఖ్య చివరి అంకె ‘4’ కనుక 20704, 2చే భాగించబడును.
20704 యొక్క చివరి రెండు స్థానాల అంకెలు 04. ఇది 41 భాగించబడును.
అదే విధముగా దత్త సంఖ్య చివరి మూడు స్థానాల అంకె 704.
ఈ సంఖ్య 8చే నిశ్శేషంగా భాగించబడును కనుక 20704 సంఖ్య 2, 4, 8లచే భాగించబడును.

ఒ) ఇచ్చివ సంఖ్య 35932.
ఈ సంఖ్య ఒకట్ల స్థానంలో ‘2’ కలదు.
కనుక దత్త సంఖ్య 2చే నిశ్శేషంగా భాగించబడును.
దత్త సంఖ్య చివరి రెండు స్థానాల అంకె 32. 32, 4చే భాగించబడును.
కనుక దత్త సంఖ్య 4చే భాగించబడును.
∴ దత్త సంఖ్య 2, 4లచే భాగించబడును.

ఓ) ఇచ్చిన సంఖ్య 85446.
ఈ సంఖ్య ఒకట్ల స్థానంలో అంకె ‘6’.
కనుక 85446, 2చే నిశ్శేషంగా భాగించబడును.
85446 ఒక అంకమూలం 8 + 5 + 4 + 4 + 6 = 27 = 2 + 7 = 9
9 అను సంఖ్య 3, మరియు 9లచే భాగించబడును.
కనుక 85446 అను సంఖ్య 3 మరియు 9లచే భాగించబడును.
∴ 85446 సంఖ్య 2, 3 మరియు 9లచే భాగించబడును.

క) ఇచ్చివ సంఖ్య 90990.
దత్త సంఖ్య యొక్క చివరి అంకే ‘0’ కనుక 90990 అనునది 2, 5 మరియు 10లచే భాగించబడును.

ఖ) ఇచ్చిన సంఖ్య 18540.
దత్త సంఖ్య యొక్క చివరి అంకె ‘0’ కనుక 18540 అనునది 2, 5 మరియు 10లచే భాగించబడును.

ప్రశ్న8.
ఇచ్చిన పంఖ్యతో భాగంచబడాలంటే ఖాళీలను సరియైవ సంఖ్యలతో పూరించండి.
అ) 395___ను 10తో
జవాబు.
395 0

ఆ) 24305___మ 9తో
జవాబు.
24305 4

ఇ) 69839___మ 3మరియు 9 తో
జవాబు.
69839 1

ఈ) 271___8 మ 6తో
జవాబు.
271 0 8

ఉ) 20710___
జవాబు.
20710___

ఊ) 5027___5ను 3మరియు 5
జవాబు.
5027 3 5

ఋ) 145___2 మ 8తో
జవాబు.
145 1 2

ఋ) 92048___మ 2తో
జవాబు.
92048___ (0/2/4/6/8)

ఎ) 23405___మ 5తో
జవాబు.
(0/5)

ప్రశ్న 9.
289279కు ఏ కనిష్ఠ సంఖ్యను కలిపితే అది రిచే నిశ్శేషంగా భాగించబడుతుంది?
జవాబు.
దత్త సంఖ్య 289279. ఈ సంఖ్య చివరి మూడు స్థానాలు 279. 279, 8చే భాగించబడును, కనుక 289279, 8చే భాగించబడును.

ఇవి చేయండి: (TextBook Page No.51 & 53)

ప్రశ్న 1.
కింది సంఖ్యల మొదటి 10 గుణిజాలు రాయండి.
అ) 3
ఆ) 5
ఇ) 8
ఈ) 9
4) 10
జవాబు.
అ) 3 యొక్క మొదటి 10 గుణిజాలు = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
ఆ) 5 యొక్క మొదటి 10 గుణిజాలు = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50.
ఇ) 8 యొక్క మొదటి 10 గుణిజాలు = 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
ఈ) 9 యొక్క మొదటి 10 గుణిజాలు = 9, 18, 27, 36, 45, 54, 63, 72, 81, 90
ఉ) 10 యొక్క మొదటి 10 గుణిజాలు = 10, 20, 30, 40, 50, 60, 70, 80, 90, 100

ప్రశ్న 2.
1 మండి 20 వరకూ సంఖ్యల మద్య గల 2, 3, … 5 గుణిజాలను విడివిడిగా రాయండి.
జవాబు.
1 నుండి 20 వరకూ ఉన్న సంఖ్యల మధ్యగల
2 గుణిజాలు = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20
1 నుండి 20 వరకూ ఉన్న సంఖ్యల మధ్యగల
3 గుణిజాలు = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
1 నుండి 20 వరకూ ఉన్న సంఖ్యల మధ్యగల
5 గుణిజాలు = 5, 10, 15, 20

ప్రశ్న 3.
7 యొక్క మొదటి 10 గుణిజాలు రాయండి.
జవాబు.
7 యొక్క మొదటి 10 గుణాలు = 7, 14, 21, 28, 35, 42, 49, 56, 63, 70.

ప్రశ్న 4.
కింది ఉన్న సంఖ్యలలో 7, 8, 10 సంఖ్యల గుణిజాలు విడివిడిగా రాయండి. 20, 14, 45, 24, 32, 35, 90, 8, 7, 10, 441, 385
జవాబు.
ఇచ్చిన సంఖ్యలలో
7 గుణిజాలు = 7, 14, 35, 385, 441
8 గుణిజాలు = 8, 24, 32
10 గుణిజాలు = 10, 20, 90

ప్రశ్న 5.
కింది వానిలో 3 గుణిజాలు కాని వాటిని గుర్తించండి.
8 26 27 32 18 45 12 28 30 66 88 48
జవాబు.
8, 26, 32, 28, 88, 48.

ప్రశ్న 6.
100 లోపు 9 యొక్క బేసి గుణిజాలు రాయండి.
జవాబు.
9, 27, 45, 63, 81, 99.

ఇవి చేయండి: (TextBook Page No.55)

ప్రశ్న 1.
కింది ఇవ్వబడిన సంఖ్యల మొదటి 10 గుణిజాలు రాసి, అందలి ఉమ్మడి గుణిజాలను వేరు చేయండి.
అ) 2 మరియు 4
ఆ) 4 మరియు 12
ఇ) 6 మరియు
ఈ) 5 మరియు 10
జవాబు.
అ) 2 యొక్క గుణిజాలు : 2, 4, 6, 8, 10, 12, 14, 16, 18, 20.
4 యొక్క గుణిజాలు : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
2 మరియు 4 యొక్క ఉమ్మడి గుణిజాలు: 4, 8, 12, 16, 20

ఆ) 4 యొక్క గుణిజాలు : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
12 యొక్క గుణిజాలు : 12, 24, 36, 48, 60, 72, 84, 96, 108, 120
4 మరియు 12 యొక్క ఉమ్మడి గుణిజాలు: 12, 24, 36

ఇ) 6 యొక్క గుణిజాలు: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60
8 యొక్క గుణిజాలు : 8, 16, 24, 32, 40, 48, 56, 64, 72, 80
6 మరియు 8 యొక్క ఉమ్మడి గుణిజాలు: 24, 48

ఈ) 5 యొక్క గుణిజాలు : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50
10 యొక్క గుణిజాలు : 10, 20, 30, 40, 50, 60, 70, 80, 90, 100
5 మరియు 10 యొక్క ఉమ్మడి గుణిజాలు 10, 20, 30, 40, 50.

ఇవి చేయండి: (TextBook Page No.57)

కింది ఇచ్చిన సంఖ్యల క.పా.గు. కనుగొనండి.
అ) 12, 15
ఆ) 16, 20
ఇ) 8, 12, 20
ఈ) 15, 20
ఉ) 6, 9, 12
జవాబు.
అ) 12 యొక్క గుణిజాలు :
12,24,36,48, 60, 72,84,96, 108, 120, …………….
15 యొక్క గుణిజాలు : – -15, 30, 45, 60, 75, 90, 105, 120, 135, 150, …………….
12 మరియు 15 యొక్క ఉమ్మడి -గుణిజాలు = 60, 120
12, 15ల క.సా.గు = 60.

ఆ) 16 యొక్క గుణిజాలు : 16, 32, 48, 64, 80, 96, 112, 128, 14, 160
20 యొక్క గుణిజాలు: – 20, 40, 60, 80, 100, 120, 140, 160, 180, 200 ……
16 మరియు 16 యొక్క ఉమ్మడి గుణిజాలు = 80, 160, …………
16, 20 క.సా.గు = 80

ఇ) 8 యొక్క గుణిజాలు : 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, …… 120, ……
12 యొక్క గుణిజాలు: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, …………..
20 యొక్క గుణిజాలు : 20, 40, 60, 80, 100, 120, 140, 160, ……………. 180, 200, …….
8, 12, 20 యొక్క ఉమ్మడి గుణిజాలు :
16 మరియు 20 = 80.
8, 12 మరియు 20ల క.సా.గు = 80

ఈ) 15 యొక్క గుణిజాలు : 15, 30, 45, 60, 75, 90, 105, 120, 135, 150 ……………
20 యొక్క గుణిజాలు : 20, 40, 60, 80, 100, 120, 140, 160, 180, 200, …………..
15 మరియు 20 యొక్క ఉమ్మడి గుణిజాలు = 60, 120
15, 20ల క.సా.గు = 60.

ఉ) 6 యొక్క గుణిజాలు : 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, ……….
9 యొక్క గుణిజాలు: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, ……….
12 యొక్క గుణిజాలు : – 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, ……….
6,9 మరియు 12 యొక్క ఉమ్మడి గుణిజాలు = 36

ఇవి చేయండి: (TextBook Page No.57)

కింది ఇచ్చిన సంఖ్యల క.సా.గు కనుగొనండి. ఏమి గమనించారు?
అ) 15, 30
ఆ) 4, 16
ఇ) 5, 15
ఈ) 6, 18
జవాబు.
అ) 15 యొక్క గుణిజాలు : 15, 30, 45, 60, 75, 90, 105, 120, 135, 150
30 యొక్క గుణిజాలు : 30, 60, 90, 120, 150, 180, 210, 240, 270, 300, …………….
15 మరియు 30 యొక్క ఉమ్మడి గుణిజాలు 30, 60, 90, 120, 150, …………….
15 మరియు 30ల క.సా.గు = 30

ఆ) 4 యొక్క గుణిజాలు : 4, 8, 12, 16, 20, 24, 28, 32,36,40, …………..
16 యొక్క గుణిజాలు : 16, 32, 48, 64, 80, 96, 112, 128, 144, 160 …………
4 మరియు 16 యొక్క ఉమ్మడి గుణిజాలు = 16, 32, 48 …………..
4మరియు 16 ల క.సా.గు = 16

ఇ) 5 యొక్క గుణిజాలు : 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, …………..
15 యొక్క గుణిజాలు : 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, ……………
5 మరియు 15 యొక్క ఉమ్మడి గుణిజాలు = 15, 30, 45, 60 …………
5 మరియు 15 ల క.సా.గు = 15

ఈ) 6 యొక్క గుణిజాలు : 6, 12, 18, 24, 30, 36, 42, 48, 54, ………….. 60, ……
18 యొక్క గుణిజాలు: 18, 36, 54, 72, 90, 108, 126, 144, 162, 180, ……………
6 మరియు 18 ల ఉమ్మడి గుణిజాలు = 18, 36, 54
6 మరియు 18ల క.సా.గు = 18.

ఇవి చేయండి: (TextBook Page No.63)

ప్రశ్న 1.
కింది సంఖ్యల కారణాంకాలు కనుక్కోండి.
అ) 21
ఆ) 38
ఇ) 72
ఈ) 96
జవాబు.
అ) 21 = 1 × 21
= 3 × 7
= 7 × 3
= 21 × 1
21 యొక్క కారణాంకాలు : 1, 3, 7, 21.

ఆ) 38 = 1 × 38
= 2 ×19
38 యొక్క కారణాంకాలు : 1, 2, 19, 38

ఇ) 72 = 1 × 72
= 2 × 36
= 3 × 24
= 4 × 18
= 6 × 12
= 8 × 9
72 యొక్క కారణాంకాలు : – 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 మరియు 72.

ఈ) 96 = 1 × 96
= 2 × 48
= 3 × 32
= 4 × 24
= 6 × 16
= 8 × 12
96 యొక్క కారణాంకాలు : 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48 మరియు 96.

ప్రశ్న 2.
మొదటి సంఖ్య రెండవ సంఖ్యకు కారణాంకమో కాదో కనుక్కోండి.
అ) 14; 322
ఆ) 26; 832
ఇ) 35; 425
ఈ) 56; 3500
ఉ) 8; 48
ఊ) 14; 37
ఋ) 15; 75
ౠ) 12; 72
జవాబు.
అ) అవును 14, 322కు కారణాంకము అగును.
ఆ) అవును 26; 832కు కారణాంకము అగును
ఇ) కాదు 35, 425కు కారణాంకము కాదు.
ఈ) కాదు 56, 3500కు కారణాంకము కాదు.
ఉ) అవును 8, 48కు కారణాంకము అగును.
ఊ) కాదు 14, 37కు కారణాంకము కాదు.
ఋ) అవును 15, 75కు కారణాంకము అగును
ఋ) అవును 12, 72కు కారణాంకము అగును

ప్రశ్న 3.
66 యొక్క అన్ని కారణాంకాలను కనుక్కోండి.
జవాబు.
66 కారణాంకాలు = 1 × 66
= 2 × 33
= 3 × 22
= 6 × 11
∴ 66 యొక్క కారణాంకాలు 1, 2, 3, 6, 11, 22, 33 మరియు 66.

ప్రశ్న 4.
64 యొక్క అన్ని సరి కారణాంకాలు రాయండి.
జవాబు.
64 యొక్క కారణాంకాలు = 1 x 64
= 2 x 32 = 4 x 16
= 8 x 8
∴ 64 యొక్క సరి కారణాంకాలు: 2, 4, 8, 16, 32 మరియు 64.

ప్రశ్న 5.
20లోపు ప్రధాన సంయుక్త సంఖ్యలమ పట్టికలో నమోదు చేయండి.

జవాబు.

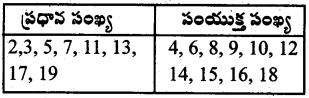
వినోద కృత్యం: (TextBook Page No.65 & 67)

ఎరటొప్తనీస్ జల్లెడ :

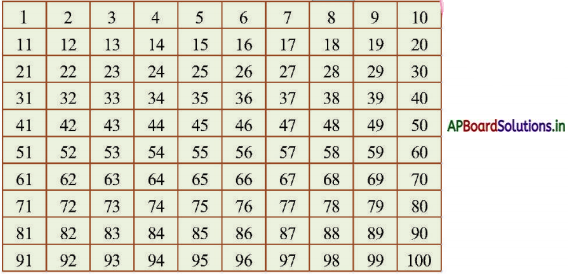
కింది ప్రశ్నలకు సమాధానాలు రాయండి :

ప్రశ్న 1.
1 నుండి 10 వరకు గల ప్రధాన సంఖ్య లేవి?
జవాబు.
2, 3, 5, 7

ప్రశ్న 2.
1 నుండి 20 వరకు గల ప్రధాన సంఖ్య లేవి?
జవాబు.
11, 13, 17, 19

ప్రశ్న 3.
20 నుండి 50 వరకు గల ప్రధాన సంఖ్య లేవి?
జవాబు.
23, 29, 31, 37, 41, 43, 47.

ప్రశ్న 4.
1 నుండి 50 వరకు గల ప్రధాన సంఖ్య లేవి?
జవాబు.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 49.

ప్రశ్న 5.
50 నుండి 100 వరకు గల ప్రధాన సంఖ్య లేవి?
జవాబు.
53, 59, 61, 67, 71, 73, 79, 83, 87, 89, 97

ప్రశ్న 6.
50 నుండి 100 వరకు గల ప్రధాన సంఖ్య ఎన్ని? వాటిని రాయండి.
జవాబు.
50 నుండి 100కు మధ్యన 10 ప్రధాన సంఖ్యలు కలవు.

ప్రశ్న 7.
1 నుండి 100 వరకు గల ప్రధాన సంఖ్యలో ఏమైనా ప్రత్యేకత ఉందా? ఏమిటది?
జవాబు.
1 నుండి 100 వరకు గల ప్రధాన సంఖ్యలలో అన్నీ బేసి సంఖ్యలు.

ప్రశ్న 8.
ప్రధాన సంఖ్యలన్నీ సరి సంఖ్యలా? బేసి సంఖ్యలా?
జవాబు.
అన్నీ బేసి సంఖ్యలే. ‘2’ తప్ప.

ఇవి చేయండి: (TextBook Page No.69)

ప్రశ్న 1.
కింద సంఖ్యలను ప్రధాన కారణాంకాల లబ్ధంగా రాయండి.
అ) 52
ఆ) 100
ఇ) 88
ఉ) 90
ఈ) 96
జవాబు.

∴ 52 యొక్క ప్రధాన కారణాంకాల లబ్ధం = 2 × 2 × 13

ఆ)

∴ 100 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 2 × 5 × 5

ఇ)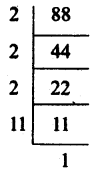

∴ 88 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 2 × 2 × 11

ఈ)

∴96 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 2 × 2 × 2 × 2 × 3

ఉ)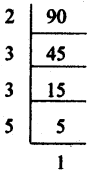

∴ 90 యొక్క ప్రధాన కారణాంకాల లబ్దం = 2 × 3 × 3 × 5

ప్రశ్న 2.
12 × 15 యొక్క ప్రధాన కారణాంకాల లబ్ధం.
జవాబు.
12 × 5 యొక్క ప్రధాన కారణాంకాల లబ్దం

∴ 12 × 15 = 2 × 2 × 3 × 3 × 5

ప్రశ్న 3.
జతపరచండి:

జవాబు.

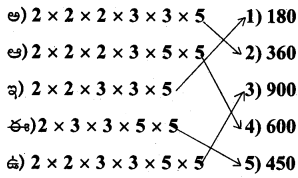
ప్రశ్న 4.
5 × 2 × 3 × 3 అనునది. ఏ సంఖ్య ప్రధాన కారణాంక లబ్ధం?
జవాబు.
90

ఇవి చేయండి: (TextBook Page No.71)

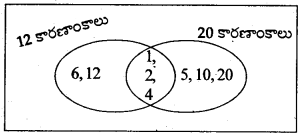
కింది సంఖ్యల ఉమ్మడి కారణాంకాలను కనుగొని వాటిని చిత్రంలో చూపండి.
a) 6 మరియు 12
b) 12 మరియు 20
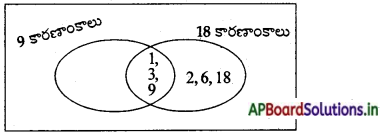
c) 9 మరియు 18
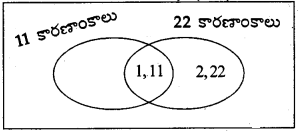
d) 11 మరియు 22
జవాబు.
a) 6 కారణాంకాలు = 1, 2, 3, 6
12 కారణాంకాలు = 1, 2, 3, 4, 6, 12

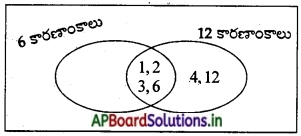
b) 12 కారణాంకాలు = 1, 2, 3, 4, 6, 12
20 కారణాంకాలు = 1, 2, 4, 5, 10, 20

c) 9 కారణాంకాలు = 1, 3, 9
18 కారణాంకాలు = 1, 2, 3, 6, 9,

d) 11 కారణాంకాలు= 1, 11
22 కారణాంకాలు = 1, 2, 11, 22

ఇవి చేయండి: (TextBook Page No.73)

ఇచ్చిన సంఖ్యల’గసాభా కనుగొనండి (ఉమ్మడి కారణాంక పద్ధతి)
1) 21 మరియు 28
2) 34 మరియు 20
3) 33 మరియు 39
4) 16 మరియు 36
5) 12 మరియు 18
6) 80 మరియు 100
జవాబు.
1) 21 = 1, 3, 7, 21
28 కారణాంకాలు = 1, 2, 4, 7, 14, 28
21 మరియు 28 ఉమ్మడి కారణాంకాలు = 1, 7
21 మరియు 28 ల గసాభా = 7 ,

2) 34 కారణాంకాలు = 1, 2, 17, 34 ……….
20 కారణాంకాలు = 1, 2, 4, 5, 10, 20
34 మరియు 20 ఉమ్మడి కారణాంకాలు = 1, 2
34 మరియు 20 ల గసాభా = 1, 2

3) 33 కారణాంకాలు = 1, 3, 11, 33
39 కారణాంకాలు = 1, 3, 13, 39
33 మరియు 39 ఉమ్మడి కారణాంకాలు = 1, 3
33 మరియు 39 ల గసాభా = 3

4) 16 కారణాంకాలు = 1, 2, 4, 8, 16
36 కారణాంకాలు = 1, 2, 3, 4, 9, 12, 18, 36
16 మరియు 36 ఉమ్మడి కారణాంకాలు= 1, 2, 4
16 మరియు 36 ల గసాభా = 4

5) 12 కారణాంకాలు = 1, 2, 3, 4, 6, 12
18 కారణాంకాలు = 1, 2, 3, 6, 9, 18
12 మరియు 18 ఉమ్మడి కారణాంకాలు = 1, 2, 3, 6
12 మరియు 18 ల గసాభా = 6

6) 80 కారణాంకాలు = 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
100 కారణాంకాలు = 1, 2, 4, 5, 10, 20, 25, 50, 100
80 మరియు 100 ఉమ్మడి కారణాంకాలు = 1, 2, 4, 5, 10, 20
80 మరియు 100ల గసాభా = 20.

ఇవి చేయండి: (TextBook Page No.73)

ఇచ్చిన సంఖ్యల గపాభా కమగొనండి ఏమి గమనించారు.
1) 4, 16
2) 4, 12
3) 5, 15
4) 14, 42
జవాబు.
1) 4 కారణాంకాలు = 1, 2, 4
16 కారణాంకాలు = 1, 2, 4, 8, 16
4మరియు 16 ఉమ్మడి కారణాంకాలు = 1,2,4
4 మరియు 16ల గసాభా = 4

2) 4 కారణాంకాలు = 1, 2, 4
12 కారణాంకాలు = 1, 2, 3, 4, 6, 12
4 మరియు 12 ఉమ్మడి కారణాంకాలు = 1, 2, 4
4 మరియు 12 ల గసాభా = 4

3) 5 కారణాంకాలు = 1, 5
15 కారణాంకాలు = 1, 3, 5, 15
5 మరియు 15 ఉమ్మడి కారణాంకాలు = 1, 5
5 మరియు 15ల గసాభా = 5

4) 14 కారణాంకాలు = 1, 2, 7
42కారణాంకాలు = 1, 2, 3, 6, 7, 14, 21, 22
14 మరియు 42 ఉమ్మడి కారణాంకాలు = 1, 2, 7
14 మరియు 42ల గసాభా = 7
గమనిక :-
ఇవ్వబడిన సంఖ్యల జతలలో ఒకటి రెండవదానికి గుణిజం అయినచో, వాటి గసాభా చిన్న సంఖ్య అవుతుంది.

ఇవి చేయండి: (TextBook Page No.73)

ప్రశ్న 1.
ప్రధాన కారణాంక విభజన పద్ధతిలో ఇచ్చి సంఖ్యల కపాగు, గపాభాలమ కమగొనండి.
అ) 15,48
ఆ) 18, 42, 48
ఇ) 15, 25, 30
ఈ) 10, 15, 25
ఉ) 15, 18, 36, 20
జవాబు.
అ) ఇచ్చిన సంఖ్యలు 15 మరియు 48

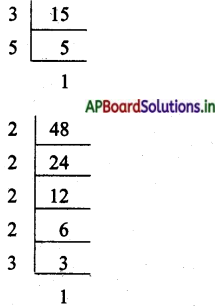
15 యొక్క ప్రధాన కారణాంకాలు = 1 × 3 × 5
48 యొక్క ప్రధాన కారణాంకాలు = 2 × 2 × 2 × 2 × 3
15 మరియు 48 ఉమ్మడి కారణాంకాలు = 1 × 3
ఇతర కారణాంకాలు = 5 × 2 × 2 × 2 × 2
కసాగు = 1 × 3 × 5 × 2 × 2 × 2 × 2 = 240
గసాభా = 1 × 3 = 3

ఆ) ఇచ్చిన సంఖ్యలు 48 18, 42, 48

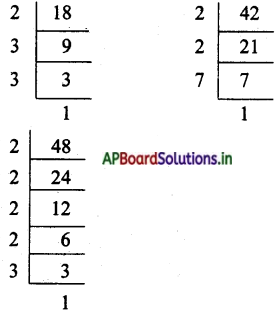
18 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 3 × 3
42 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 3 × 7
ఉమ్మడి కారణాంకాలు = 1 × 2 × 3
ఇతర కారణాంకాలు = 3 × 7 × 2 × 2 × 2
కసాగు = 1 × 2 × 3 × 3 × 7 × 2 × 2 × 2 = 1008
గసాభా = 1 × 2 × 3 = 6

ఇ) ఇచ్చిన సంఖ్యలు 15, 25 మరియు 30

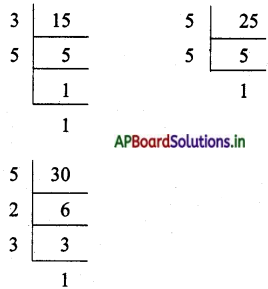
15 యొక్క ప్రధాన కారణాంకాలు = 1 × 3 × 5
15 యొక్క ప్రధాన కారణాంకాలు = 1 × 5 × 5
30 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 3 × 5
ఉమ్మడి కారణాంకాలు = 1 × 5
ఇతర కారణాంకాలు = 3 × 3 × 5 × 2
కసాగు = 1 × 5 × 3 × 3 × 5 × 2 = 450
గసాభా = 1 × 5 = 5

ఈ) ఇచ్చిన సంఖ్యలు 10, 15 మరియు 25

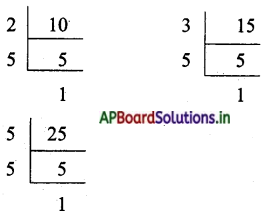
10 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 5
15 యొక్క ప్రధాన కారణాంకాలు = 1 × 3 × 5
25 యొక్క ప్రధాన కారణాంకాలు = 1 × 5 × 5
ఉమ్మడి కారణాంకాలు = 1 × 5 = 5
ఇతర కారణాంకాలు = 2 × 3 × 5 = 30
కసాగు = 5 × 30 = 150
గసాభా = 5

ఉ) ఇచ్చిన సంఖ్యలు 15, 18, 36 మరియు 20

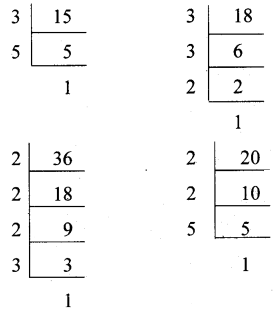
15 యొక్క ప్రధాన కారణాంకాలు = 1 × 3 × 5
8 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 3 × 3
36 యొక్క ప్రధాన కారణాంకాలు = 1 × 3 × 3 × 2 × 2
20 యొక్క ప్రధాన కారణాంకాలు = 1 × 2 × 2 × 5
ఉమ్మడి కారణాంకాలు = 1
ఇతర కారణాంకాలు = 3 × 5 × 2 × 3 × 3 × 3 × 2 × 2 × 2 × 5 = 194, 400
కసాగు = 194, 400
గసాభా = 1.

ప్రశ్న 2.
భాగహార పద్ధతిలో కపాగు, గసాభా కనుగొనండి.
అ) 16, 28, 36
ఆ) 12, 18, 42
ఇ) 30, 75, 90
ఈ) 24, 32, 48
ఉ) 12, 15, 18
జవాబు.
అ) ఇచ్చిన సంఖ్యలు 16, 28 మరియు 36.

కసాగు = 2 × 2 × 4 × 7 × 9 = 1008
గసాభా = 2 × 2 = 4

ఆ) ఇచ్చిన సంఖ్యలు 12, 18 మరియు 42

కసాగు = 2 × 3 × 2 × 3 × 7 = 252
గసాభా = 2 × 3 = 6

ఇ) ఇచ్చిన సంఖ్యలు 30, 75, 90

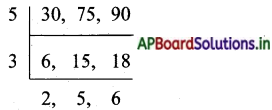
కసాగు = 5 × 3 × 2 × 5 × 6 = 900
గసాభా = 5 × 3 = 15

ఈ) ఇచ్చిన సంఖ్యలు 24, 32, 48

కసాగు = 4 × 2 × 3 × 4 × 6 = 576
గసాభా = 4 × 2 = 8

ఉ) ఇచ్చిన సంఖ్యలు 12, 15 మరియు 18

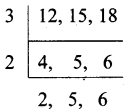
కసాగు = 3 × 2 × 2 × 5 × 6 = 360
గసాభా = 3.

అభ్యాసం 3:

కింద పద సమస్యలను సాధించుము :

ప్రశ్న 1.
ఒక బుట్టలో కొన్ని పండ్లు కలవు. ఆ పండ్లను కుప్పకు 4 లేదా 6 లేదా 8 లేదా 10 చొప్పున పేర్చి. ఒక్క పండు కూడా మిగలకుండా ఉండాలంటే ఆ బుట్టలో ఉండవలసిన కనీస పండ్ల సంఖ్య ఎంత?

జవాబు.
పండ్లను కుప్పకు 4 లేదా 6 లేదా 8 లేదా 10 చొప్పున పేర్చి ఒక్క పండు కూడా మీగలకుండా ఉండుటకు 4, 6, 8, 10ల కసాగును కనుగొనవలెను.

కసాగు = 2 × 2 × 1 × 3 × 2 × 5 = 120
∴ బుట్టలో ఉండవలసిన కనీస పండ్ల సంఖ్య = 120

ప్రశ్న 2.
రాము దగ్గర 16 నీలం రంగు గోళీలు, 12 తెల్ల గోళీలు ఉన్నాయి. అతను వాటిని ఒక్క గోళీ కూడా మిగలకుండా సమాన సమూహాలుగా చేయాలంటే ఒక్కొక్క సముహంలో ఉండవలసిన గరిష్ఠ గోళీల సంఖ్య ఎంత?

జవాబు.
రాము వద్ద గల నీలం గోళీలు సంఖ్య 16, తెల్ల గోళీలు సంఖ్య 12, 16

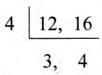
∴ గసాభా = 4
ఒకోక్క సమూహములో ఉండవలసిన గరిష్ఠ గోళీల సంఖ్య = 4.

ప్రశ్న 3.
ఒక నియాన్ బల్బులను ఒకేసారి స్విచ్ వేయగా ఒకటి ప్రతి 4 సెకన్లకు మరొకటి ప్రతి 6 సెకన్లకు బ్లింక్ అవుతుంది. ఒక నిమిషంలో ఎన్నిసార్లు ఒకేసారి బ్లింక్ అవుతాయి.

జవాబు.
రెండు నియాన్ బల్బులు ఒకేసారి స్విచ్ వేయగా అవి బ్లింక్ చేయు సమయం = 4 సెకన్లు మరియు 6 సెం.మీ
4 మరియు 6ల కసాగు

కసాగు = 2 × 2 × 3 = 12 సెకన్లు
బల్బులు ఒకేసారి బ్లింక్ చేయు సమయం = 12 సెకన్లు
ఇచ్చిన సమయం = 60 సెకన్లు = ఒక నిమిషం
∴ ఒక నిమిషంలో అవి ఒకేసారి బ్లింక్ అగు సమయం = 60 ÷ 12 = 5 సార్లు.

ప్రశ్న 4.
40 మంది బాలికలు, 32 మంది బాలురు రాష్ట్రస్థాయి ఆటల పోటీలలో పాల్గొనదలచి నారు. ప్రతి టీమ్ నందు బాలురు, బాలికల సంఖ్య సమానంగా ఉండాలి.
1) ప్రతి జట్టులో ఉండే గరిష్ఠ విద్యార్థుల సంఖ్య ఎంత ?
2) ఒక్కొక్క జట్టులోని బాలురు, బాలికల సంఖ్య ఎంత?

జవాబు.
రాష్ట్రస్థాయి పోటీల్లో పాల్గొన్న బాలికలు, బాలురు సంఖ్య వరుసగా 40 మరియు 32.
i) ప్రతి జట్టులోనూ ఉండే గరిష్ఠ విద్యార్థుల సంఖ్యను కల్గొనొనుటకు గసాభా కల్గొనవలెను.
32 మరియు 40ల గసాభా.

∴ గసాభా. = 2 × 2 × 2 = 8
ప్రతీ బుట్టలో ఉండదగు గరిష్ఠ సభ్యుల సంఖ్య = 8 మంది

ii) ఒక్కొక్క బుట్టలో ఉండదగు బాలురు, బాలికల సంఖ్యను కనుగొనుటకు కసాగును. చేయాలి.

∴ 32 మరియు 4ల కసాగు = 2 × 2 × 2 × 4 × 5 = 160.

ప్రశ్న 5.
ఒక్కొక్క నోట్ పుస్తకంలో 32 పేజీలు లేదా 40 పేజీలు లేదా 48 పేజీలు ఉండేలా పుస్తకాలు తయారు చేయాలంటే కావలసిన కనీస సంఖ్య ఎంత?

జవాబు.
కావలసిన పేపర్లు కనీస సంఖ్యనుసార కనొనుటకు 32, 40, 48ల కసాగును చేయాలి.

కసాగు = 2 × 2 × 2 × 4 × 5 × 6 = 960

∴ 960 ఇచ్చిన పేజీలు ఉండేలా పుస్తకాలు తయారు చేయుటకు 960 కనీస పేజీలు కావలెను.

ప్రశ్న 6.
ఒక ఆడిటోరియం నందు వరుసకు 27 కుర్చీలు లేదా 33 కుర్చీలు ఉండేలా ఏర్పాటు చేయాలంటే కావలసిన కనీస కుర్చీల సంఖ్య ఎంత?

జవాబు.
కావలసిన కనీస కుర్చీలు సంఖ్యను ఏర్పాటు చేయుటకు 27 మరియు 33ల కసాగు కల్గొనవలెను.

27 మరియు 33ల కసాగు = 3 × 9 × 11 = 297
∴ 297 కనీస కుర్చీలు అవసరము.