Andhra Pradesh AP Board 5th Class Maths Solutions 8th Lesson Fractions Textbook Exercise Questions and Answers.
AP State Syllabus 5th Class Maths Solutions Chapter 8 Fractions
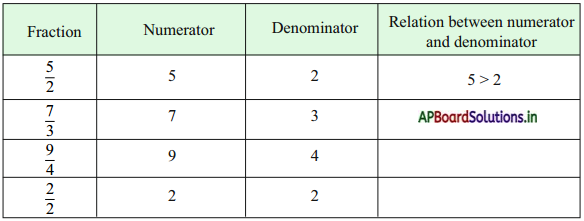
I. Observe the following table.
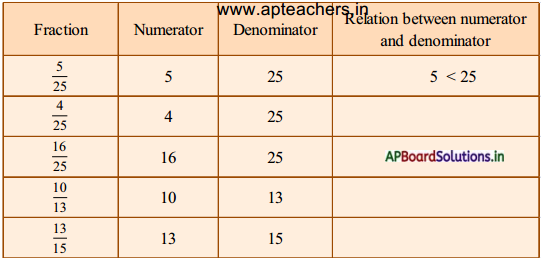
Answer:
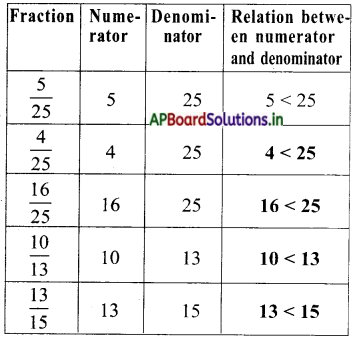
What do you observe from the above table?
Answer:
Here, in all fractions the numerator is less than the denominator.
![]()
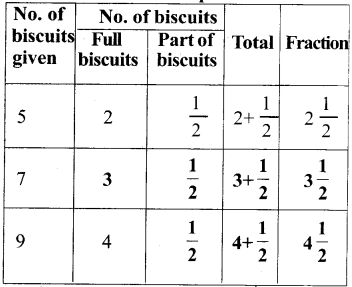
II. If Hema and Gopi got 7 and 9 biscuits then complete this table.
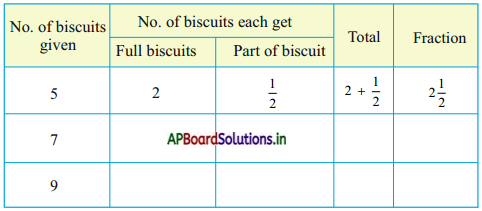
Answer:
III. Observe the fractions : \(\frac{3}{4}, \frac{4}{5}, \frac{6}{7}, \frac{12}{13}, \frac{25}{28}\)
Answer:
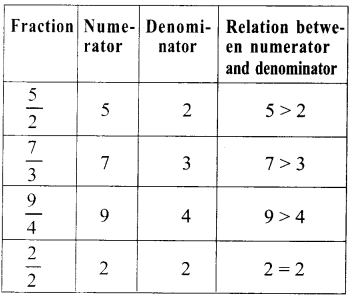
What do you say?
Answer:
Here is all fractions have numerator is greater than or equal to denominator. These types of fractions are called improper fractions.
![]()
Do this: (TextBook Page No.129)
Question 1.
Write any 5 proper fractions.
Answer:
Proper fractions: \(\frac{3}{4}, \frac{4}{5}, \frac{6}{7}, \frac{12}{13}, \frac{25}{28}\)
Question 2.
Write any 5 1m proper fractions.
Answer:
Improper fractions: \(\frac{7}{6}, \frac{26}{22}, \frac{21}{20}, \frac{28}{25}, \frac{13}{12}\)
Question 3.
Write any 5 mixed fractions.
Answer:
Mixed fractions: \(3 \frac{2}{3}, 7 \frac{1}{2}, 9 \frac{3}{5}, 8 \frac{2}{3}, 6 \frac{5}{7}\)
Question 4.
Convert these fraction into mixed fraction \(\frac{5}{2}, \frac{7}{3}, \frac{9}{4}, \frac{11}{2}\)
Answer:
Conversion of fraction into mixed fraction.

Question 5.
Convert these fractions into improper fraction \(4 \frac{2}{3}, 5 \frac{3}{4}, 6 \frac{2}{5}, 3 \frac{1}{2}\).
Answer:
Conversion of Mixed fractions into improper fractions
\(3 \frac{1}{2}=\frac{2 \times 3+1}{2}=\frac{7}{2}\).
![]()
Do this: (TextBook Page No. 132)
Question 1.
Write any three equivalent fractions to the given fractions.
a) \(\frac{4}{8}\)
b) \(\frac{1}{3}\)
c) \(\frac{3}{7}\)
d) \(\frac{20}{24}\)
Answer:
a) Equivalent fractions to \(\frac{4}{8}=\frac{8}{16}=\frac{12}{24}=\frac{16}{32}\)
b) Equivalent fractions to \(\frac{1}{3}=\frac{3}{9}=\frac{2}{6}=\frac{4}{12}\)
c) Equivalent fractions to \(\frac{3}{7}=\frac{9}{21}=\frac{6}{14}=\frac{12}{28}\)
d) Equivalent fractions to \(\frac{20}{24}=\frac{40}{48}=\frac{60}{72}=\frac{80}{96}\)
Exercise 1:
Question 1.
Simplify the following fractions. (by cancellation method).
(i) \(\frac{105}{15}\)
(ii) \(\frac{200}{20}\)
(iii) \(\frac{7}{10}\)
(iv) \(\frac{666}{66}\)
(v) \(\frac{125}{1000}\)
(vi) \(\frac{120}{200}\)
Answer:

![]()
Question 2.
Simplify the following fractions. (by H.C.F. method)
(i) \(\frac{12}{18}\)
(ii) \(\frac{14}{35}\)
(iii) \(\frac{22}{55}\)
(iv) \(\frac{27}{36}\)
(v) \(\frac{128}{164}\)
(vi) \(\frac{210}{427}\)
Answer:
(i) HCF of 12 and 18 is 6.
\(\frac{12 \div 6}{18 \div 6}=\frac{2}{3}\)
So, \(\frac{2}{3}\) is the simplest form of \(\frac{12}{18}\).
(ii) HCF of 14 and 35 is 7.
\(\frac{14 \div 7}{35 \div 7}=\frac{2}{5}\)
So, \(\frac{2}{5}\) is the simplest form of \(\frac{14}{35}\).
(iii) HCF of 22 and 55 is 11.
\(\frac{22 \div 11}{55 \div 11}=\frac{2}{5}\)
So, \(\frac{2}{5}\) is the simplest form of \(\frac{22}{55}\).
(iv) HCF of 27 and 36 is 9.
\(\frac{27 \div 9}{36 \div 9}=\frac{3}{4}\)
So, \(\frac{3}{4}\) is the simplest form of \(\frac{27}{36}\).
(v) HCF of 128 and 164 is 4.
\(\frac{128 \div 4}{164 \div 4}=\frac{32}{41}\)
So, \(\frac{32}{41}\) is the simplest form of \(\frac{128}{164}\).
(vi) HCF of 210 and 427 is 7.
\(\frac{210 \div 7}{427 \div 7}=\frac{30}{61}\)
So, \(\frac{30}{61}\) is the simplest form of \(\frac{210}{427}\).
Question 3.
Convert the following fractions into the simplest form by both the methods.
(i) \(\frac{16}{64}\)
(ii) \(\frac{12}{18}\)
(iii) \(\frac{30}{50}\)
(iv) \(\frac{40}{25}\)
(v) \(\frac{16}{32}\)
(vi) \(\frac{8}{40}\)
Answer:
(i) 1s tMethod: HCF of 16 and 64 is 4.
\(\frac{16 \div 4}{64 \div 4}=\frac{4}{16}=\frac{1}{4}\)
So, \(\frac{1}{4}\) is the simplest form of \(\frac{16}{64}\).
2nd Method = 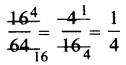
(ii) 1st Method HCF of 12 and 28 is 4.
\(\frac{12 \div 4}{28 \div 4}=\frac{3}{7}\),
So \(\frac{3}{5}\) is simplest form of \(\frac{12}{28}\) .
2nd Method: = 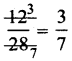
![]()
iii) 1st Method : HCF of 30 and 50 is 10.
\(\frac{30 \div 10}{50 \div 10}=\frac{3}{5}\)
So, \(\frac{3}{5}\) is simplest form of \(\frac{30}{50}\)
2nd method \(\frac{30}{50}=\frac{3}{5}\).
(iv) 1st method: HCF of 40 and 25 is 5
\(\frac{40 \div 5}{25 \div 5}=\frac{8}{5}\)
So \(\frac{8}{5}\) is simplest form of \(\frac{40}{25}\)
2nd method: 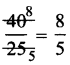
(v) 1st method: HCF of 16 and 32 is 16.
\(\frac{16+16}{32+16}=\frac{1}{2}\),
So \(\frac{1}{2}\) is the simplest form of \(\frac{16}{32}\).
2nd method: 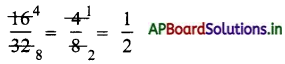
vi) 1st method: HCF of 8 and 40 is 8.
\(\frac{8 \div 8}{40 \div 8}=\frac{1}{5}\),
So \(\frac{1}{5}\) is simplest form of \(\frac{8}{48}\).
2nd method: 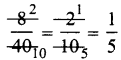
Question 4.
To get equivalent fractions what should we do a given fraction ?
Answer:
To get equivalent fractions, we multiply / divide both numerator and denominator by the same number.
Question 5.
Write any three equivalent fractions to the given fractions.
(i) \(\frac{5}{8}\)
(ii) \(\frac{32}{64}\)
(iii) \(\frac{3}{7}\)
(iv) \(\frac{125}{255}\)
(v) \(\frac{7}{10}\)
Answer:
(i) Equivalent fractions to \(\frac{5}{8}\) is \(\frac{10}{16}, \frac{15}{24} \text { and } \frac{20}{32}\)
(ii) Equivalent fractions to \(\frac{1}{2}, \frac{2}{4}, \frac{4}{8}, \frac{8}{16}\)
(iii) Equivalent fractions to \(\frac{3}{7}\) is \(\frac{6}{14}, \frac{9}{21}, \frac{12}{28\)
(iv) Equivalent fractions to \(\frac{125}{255}\) is \(\frac{5}{9}, \frac{25}{45} \text { and }\)
(v) Equivalent fractions to \(\frac{7}{10}\) is \(\frac{14}{20}, \frac{21}{30}\) and \(\frac{35}{50}\)
Question 6.
Govindamma distributed her 4 acrse of land to her 3 sons, then write the part of land each got in the form of a fraction.
Answer:
Total land = 4 acres
No. of sons = 3
Part of land each got in the form of fraction = \(\frac{4}{3}\) = 1\(\frac{1}{3}\).
![]()
Do these : (TextBook Page No.137)
Question 1.
Observe the example and write the correct fractions in the other circles.
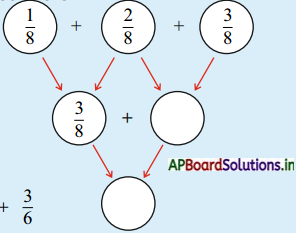
Answer:
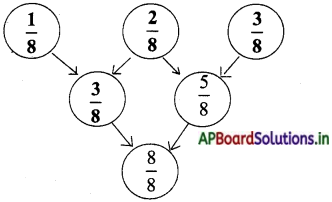
Question 2.
Find the sum.
(i) \(\frac{2}{10}+\frac{4}{10}\)
(ii) \(\frac{2}{6}+\frac{3}{6}\)
(iii) \(1 \frac{1}{4}+3 \frac{1}{4}\)
(iv) \(2 \frac{1}{5}+3 \frac{1}{5}\)
Answer:
(i) \(\frac{2}{10}+\frac{4}{10}=\frac{2+4}{10}=\frac{6}{10}\)
(ii) \(\frac{2}{6}+\frac{3}{6}=\frac{2+3}{6}=\frac{5}{6}\)
(iii) \(1 \frac{1}{4}+3 \frac{1}{4}=\frac{5}{4}+\frac{13}{4}=\frac{18}{4}\)
(iv) \(2 \frac{1}{5}+3 \frac{1}{5}=\frac{11}{5}+\frac{16}{5}+\frac{27}{5}\)
Question 3.
\(\frac{1}{2}\) kg of a sugar packet, \(\frac{3}{6}\) kg of jaggery are in a bag. Then what is the
total weight of two items in the bag?
Answer:
Weight of sugar packet = \(\frac{1}{2}\) kg
Weight ofjaggery packet = \(\frac{3}{6}\) kg = \(\frac{1}{2}\) kg
Total weight of two items = \(\frac{1}{2}\) + \(\frac{3}{6}\)
\(\frac{3}{6}+\frac{3}{6}=\frac{3+3}{6}=\frac{6}{6}\) = 1.
![]()
Question 4.
Sakru paints \(\frac{1}{5}\) th part of a wall on first day. \(\frac{2}{5}\) th part of the wall on second day Then how much part lie painted in both the days?
Answer:
Painting part of wall on first day = \(\frac{1}{5}\)
Painting part of wall on second day = \(\frac{2}{5}\)
Painting part of wall on both the days = \(\frac{1}{5}+\frac{2}{5}=\frac{1+2}{5}=\frac{3}{5}\)
Question 5.
Polamma had some money. She spent \(\frac{3}{6}\)th part of money on books. \(\frac{1}{6}\) th part of money on pens, pencils and erasers. Then how much part money did she spend ¡n total?
Answer:
Money spent on books = \(\frac{3}{6}\)th part
Money spent on pens = \(\frac{1}{6}\)th part
pencils and erasers.
Money spent in total = \(\frac{3}{6}+\frac{1}{6}=\frac{3+1}{6}\) = \(\frac{4}{6}\)th part
Do these: (TextBook Part No. 139)
Question 1.
Complete this.
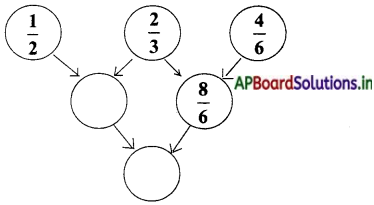
Answer:
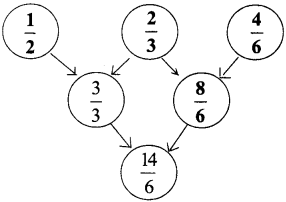
![]()
Question 2.
Find the sum.
(i) \(\frac{1}{5}+\frac{3}{4}\)
(ii) \(\frac{3}{4}+\frac{5}{6}\)
(iii) \(1 \frac{2}{3}+2 \frac{5}{6}\)
(iv) \(3 \frac{1}{8}+2 \frac{5}{6}\)
Answer:
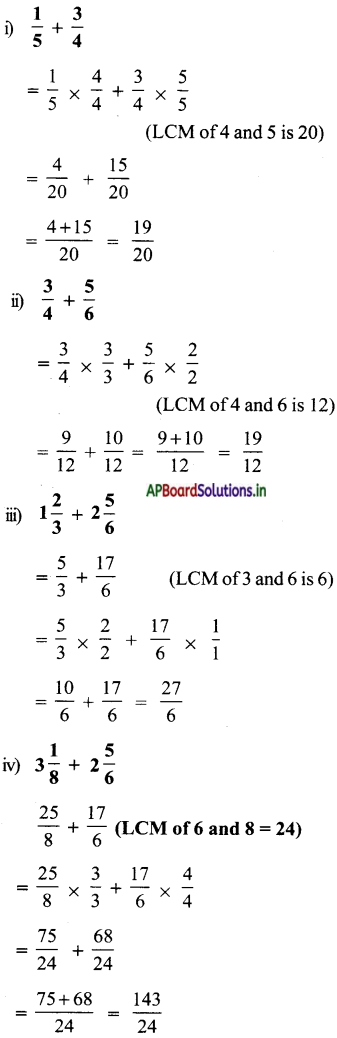
![]()
Question 3.
Seetamma read \(\frac{1}{5}\) th part of a book on Monday, \(\frac{4}{10}\) part of the book on Tuesday. Then how much part did she complete on two days ?
Answer:
Book read on Monday = \(\frac{1}{5}\) th part
Book read on Tuesday = \(\frac{4}{10}\) th part
Book read on two days = \(\frac{1}{5}\) + \(\frac{4}{10}\)
LCM of 5 and 10 is 10.
= \(\frac{1}{5} \times \frac{2}{2}+\frac{4}{10} \times \frac{1}{1}\)
= \(\frac{2}{10}+\frac{4}{10}=\frac{2+4}{10}=\frac{6}{10}\)
Question 4.
Polayya painted a wall of \(\frac{3}{4}\) th part on 1st day and \(\frac{3}{6}\) th part of the wall on 2nd day. Then how much part he painted the wall in two days ?
Answer:
Painted part of wal on 1 st day = \(\frac{1}{5}\)
Painted part of wall on 2nd day = \(\frac{3}{6}\)
Painted part in two days = \(\frac{1}{5}\) + \(\frac{3}{6}\)
LCM of 5 and 6 is = 30
= \(\frac{1}{5} \times \frac{6}{6}+\frac{3}{6} \times \frac{5}{5}=\frac{21}{30}=\frac{7^{t h}}{10} \text { Part }\)
Try this: (TextBook Part No.139)
Question 1.
Add \(5 \frac{6}{8}+4 \frac{1}{7}\)
Answer:

![]()
Do this: (TextBook Page No.141)
Question 1.
Complete this:
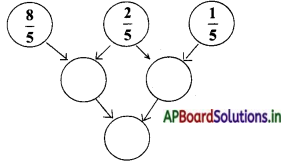
Answer:
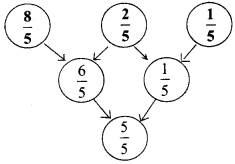
Question 2.
Do the following.
(i) \(\frac{6}{10}-\frac{1}{10}\)
(ii) \(\frac{3}{15}-\frac{1}{15}\)
(iii) \(1 \frac{3}{15}-1 \frac{1}{15}\)
(iv) \(2 \frac{4}{7}-1 \frac{2}{7}\)
Answer:
(i) \(\frac{6}{10}-\frac{1}{10}\)
= \(\frac{6-1}{10}=\frac{5}{10}\)
(ii) \(\frac{3}{15}-\frac{1}{15}\)
= \(\frac{3-1}{15}-\frac{2}{15}\)

![]()
Question 3.
Eswar painted \(\frac{1}{6}\) th part of a wall on first day. Then how much part will remain to complete?
Answer:
Painted part ofwal on Sunday = \(\frac{1}{6}\)th part
Total part = 1
Remaining part to complete = \(\frac{1}{1}-\frac{1}{6}\)
LCM of 1 and 6 is 6.
= \(\frac{1}{1} \times \frac{6}{6}-\frac{1}{6} \times \frac{1}{1}=\frac{6}{6}-\frac{1}{6}\)
= \(\frac{6-1}{6}-\frac{5}{6}\).
Question 4.
Gown completed \(\frac{1}{4}\) part of her homework on Sunday. \(\frac{5}{12}\) part on Sunday morning. How much part did she complete? How much part of home work is left?
Answer:
Work complete on Saturday = \(\frac{1}{4}\)
Work completed on Sunday = \(\frac{5}{12}\)
Work completed both days = \(\frac{1}{4}\) + \(\frac{5}{12}\)
LCM of 4 and 12 is 12.
= \(\frac{1}{4} \times \frac{3}{3}+\frac{5}{12} \times \frac{1}{1}\)
= \(\frac{3}{12}+\frac{5}{12}=\frac{3+5}{12}=\frac{8}{12}\)
Remainig part left = \(\frac{1}{1}-\frac{8}{12}\)
LCM of 1 and 12 is 12
= \(\frac{1}{1} \times \frac{12}{12}-\frac{8}{12} \times \frac{1}{1}\)
= \(\frac{12}{12}-\frac{8}{12}=\frac{12-8}{12}=\frac{4}{12}=\frac{1}{3} \text { th part }\)
Try these: (TextBook Part No.142)
Question 1.
Complete this:
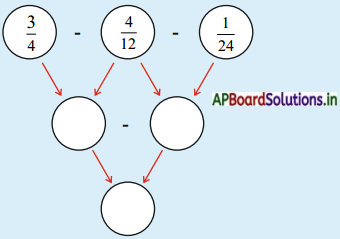
Answer:
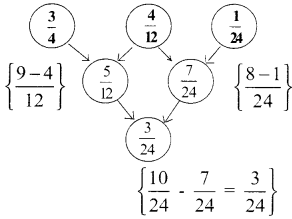
![]()
Exercise 2:
Question 1.
Do the following:
a) \(\frac{3}{4}+\frac{7}{4}\)
b) \(1 \frac{1}{2}\)
c) \(\frac{8}{3}+\frac{2}{5}\)
d) \(\frac{6}{3}+\frac{7}{4}\)
e) \(\frac{3}{5}+\frac{9}{11}\)
f) \(\frac{10}{10}+\frac{5}{20}\)
g) \(\frac{9}{10}+\frac{4}{15}\)
h) \(\frac{5}{20}+\frac{13}{30}\)
Answer:
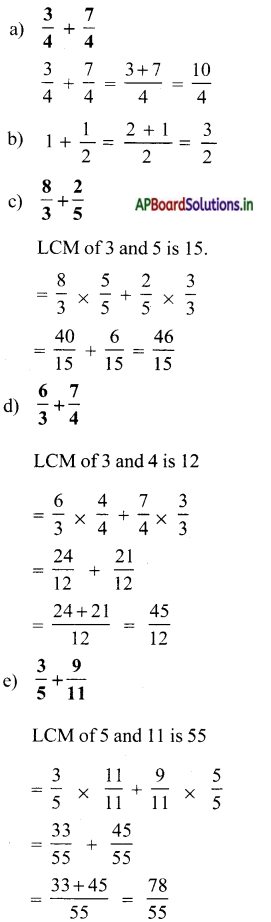

![]()
Question 2.
Do the following.
a) \(\frac{3}{7}-\frac{1}{7}\)
b) 6 – \(\frac{1}{3}\)
c) \(\frac{3}{8}-\frac{3}{16}\)
d) \(\frac{8}{7}-\frac{5}{8}\)
e) \(\frac{8}{7}-\frac{5}{8}\)
f) \(\frac{13}{15}-\frac{7}{20}\)
g) \(\frac{63}{40}-\frac{9}{10}\)
h) \(\frac{7}{15}-\frac{3}{10}\)
Answer:
a) \(\frac{3}{7}-\frac{1}{7}\)
= \(\frac{3-1}{7}-\frac{2}{7}\)
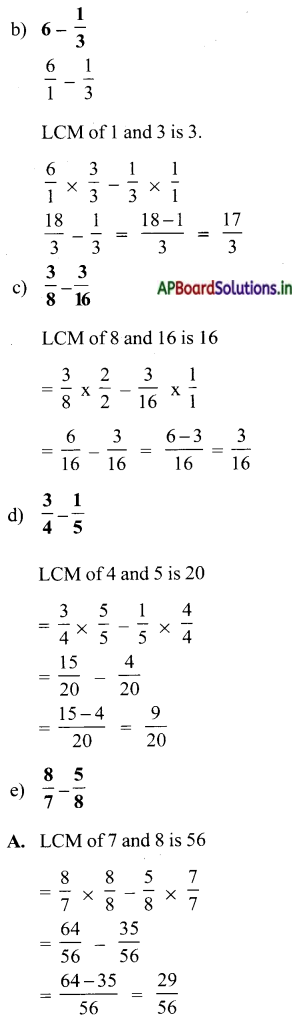

![]()
Question 3.
Find the difference between 5\(\frac{1}{3}\) and 2\(\frac{4}{7}\)
Answer:
\(\frac{15+1}{3}-\frac{14+4}{7}=\frac{16}{3}-\frac{18}{7}\)
LCM of 3 and 7 = 21
\(\frac{16}{3} \times \frac{7}{7}-\frac{18}{7} \times \frac{3}{3}\)
= \(\frac{112}{21}-\frac{54}{21}=\frac{58}{21}\)
Question 4.
Seetha purchased 1\(\frac{1}{2}\) litre of sunflower oil, \(\frac{3}{4}\) litre of groundnut oil. How much of oil she purchased in total?
Answer:
Purchased quantity of sunflower oil = 1\(\frac{1}{2}\) litr.
Purchased quantity of ground nut oil = \(\frac{3}{4}\) litr.
Purchased quantity of total oil = 1 \(\frac{1}{2}\) + \(\frac{3}{4}\)
= \(\frac{3}{2}\) + \(\frac{3}{4}\)
LCM of 2, 4 is 4
= \(\frac{3}{2} \times \frac{2}{2}+\frac{3}{4} \times \frac{1}{1}\)
= \(\frac{6}{4}+\frac{3}{4}=\frac{6+3}{4}=\frac{9}{4}\)
Question 5.
Vimala purchased 1 \(\frac{3}{4}\) m of cotton cloth for skirt, \(\frac{3}{4}\) m of cloth for blouse. How much cloth is purchased by her?
Answer:
Purchased cloth for skirt = 1 \(\frac{3}{4}\) m
Purchased cloth for blouse = \(\frac{3}{4}\) m
Purchased cloth Total = 1\(\frac{3}{4}\) + \(\frac{3}{4}\)
= \(\frac{7}{4}\) + \(\frac{3}{4}\) = \(\frac{10}{4}\) m.
![]()
Question 6.
A water tank is filled with \(\frac{9}{10}\)th part of water, but \(\frac{3}{5}\) th part of water is consumed in a day. Then find the remaining part of water in the tank?
Answer:
Total quantity of water infilled in tank = \(\frac{9}{10}\) th part
Consumed quantity of water is = \(\frac{3}{5}\) th part
Remaining part of water in the tank = \(\frac{9}{10}-\frac{3}{5}=\frac{9-6}{10}=\frac{3}{10} \text { th part }\)
Do these: (TextBook Page No.145)
Question 1.
Read 485.267
Answer:
Four hundred and eighty five (point) two six seven.
Question 2.
Write the place value of all digits in 293.819
Answer:
Given numbers = 293.819
place valu e of 2 = 200
place value of 9 = 90
place value of 5 = 5
place value of 8 = \(\frac{1}{80}\)
place value of 1 = \(\frac{1}{900}\)
place value of 9 = \(\frac{9}{1000}\)
Question 3.
Write any 5 examples for decimal fractions.
Answer:
(i) \(\frac{4756}{100}\) = 47.56
(ii) \(\frac{87685}{1000}\) = 87.685
(iii) \(\frac{763407}{1000}\) = 763.407
(iv) \(\frac{86734}{10000}\) = 8.6734
(v) \(\frac{96302}{10}\)= 9630.2
![]()
Exercise 3:
Question 1.
Fill in the blanks:
a) In improper fraction, numerator is ………………… than the denominator.
Answer:
greater
b) \(\frac{6}{6}\) is ………………… fraction (which type?)
Answer:
improper
c) 3\(\frac{1}{2}\) is ………………… fraction (which type?)
Answer:
mixed
d) \(\frac{9}{6}\) ………………… is fraction (which type?)
Answer:
improper
e) \(\frac{2}{5}\) is ………………… fraction (which type?)
Answer:
proper
f) A function having whole number and proper fraction is called ………………… fraction.
Answer:
(mixed)
Question 2.
Convert \(\frac{9}{6}\) into mixed fraction.
Answer:
Mixed fraction of \(\frac{9}{6}=1 \frac{3}{6}\).
Question 3.
Convert 2\(\frac{1}{5}\) into an improper fraction.
Answer:
Improper fraction of \(2 \frac{1}{5}=\frac{2 \times 5+1}{5}=\frac{11}{5}\).
![]()
Question 4.
Write any 5 equivalent fractions to \(\frac{2}{3}\).
Answer:
Equivalent fractions of \(\frac{2}{3}\) is \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}\) and \(\frac{16}{18}\).
Question 5.
Write simplest form of fraction for \(\frac{25}{75}\).
Answer:
Cancilation method: = 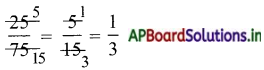
∴ Simplest form of \(\frac{25}{75}\) is \(\frac{1}{3}\).
Question 6.
Write two equivalent fractions to \(\frac{64}{36}\).
Answer:
Equivalent fractions to \(\frac{64}{36}\)
= \(\frac{64 \div 2}{36 \div 2}=\frac{32}{18}\)
= \(\frac{64 \div 4}{36 \div 4}=\frac{16}{9}\).
Question 7.
Classify the following as like and unlike frations.
\(\frac{3}{5}, \frac{2}{7}, \frac{8}{5}, \frac{9}{5}, \frac{8}{4}, \frac{1}{5}\)
Answer:
Like fractions: \(\frac{1}{5}, \frac{3}{5}, \frac{8}{5}, \frac{9}{5}\)
Unlike fractions = \(\frac{2}{7}, \frac{8}{4}\).
![]()
Question 8.
Fill in the blanks.
a) \(\frac{15}{20}=\frac{3}{\square}\)
b) \(\frac{2}{5}=\frac{\square}{50}\)
c) \(\frac{3}{5}=\frac{\square}{30}\)
Answer:
a) \(\frac{15}{20}=\frac{3}{4}\)
b) \(\frac{2}{5}=\frac{20}{50}\)
c) \(\frac{3}{5}=\frac{18}{30}\)
Question 9.
Fill in the blanks with = or ≠ (≠ denotes not equal to)
a) \(\frac{1}{2}\) ____ \(\frac{8}{16}\)
b) \(\frac{9}{15}\) ____ \(\frac{27}{30}\)
c) \(\frac{6}{13}\) ____ \(\frac{12}{39}\)
Answer:
a) \(\frac{1}{2}\) = \(\frac{8}{16}\)
b) \(\frac{9}{15}\) ≠ \(\frac{27}{30}\)
c) \(\frac{6}{13}\) ≠ \(\frac{12}{39}\)
Question 10.
Fill in the blanks with equivalent fractions.
a) \(\frac{1}{2}\) —- \(\frac{8}{16}\) ____, ____, ____
Answer:
a) \(\frac{1}{2}\) —- \(\frac{8}{16} \frac{2}{4}, \frac{3}{6}, \frac{5}{10}\).
Question 11.
a) \(\frac{6}{5}+\frac{1}{5}\) = ———-
b) \(\frac{5}{7}+\frac{2}{14}\) = ———-
c) \(\frac{15}{32}+\frac{3}{8}\) = ———-
d) \(\frac{11}{16}+1 \frac{1}{8}\) = ———-
Answer:

![]()
Question 12.
Kavitha studied \(\frac{1}{2}\) part of a book on 1st day, \(\frac{1}{3}\) part on 2nd day. then how much part she studied in both the days ?
Answer:
On I st day completed book part = \(\frac{1}{2}\)
On 2nd day completed book part = \(\frac{1}{3}\)
On both days completed book part = \(\frac{1}{2}\) + \(\frac{1}{3}\)
LCM of 2 and 3 is 6.
= \(\frac{1}{2} \times \frac{3}{3}+\frac{1}{3} \times \frac{2}{2}\)
= \(\frac{3}{6}+\frac{2}{6}\)
= \(\frac{3+2}{6}=\frac{5}{6}\).
Question 13.
Koushik went to school km by walk. He went on bicycle with his friend for the remaining distance \(\frac{3}{4}\) km. Then find the distance to school from his house.
Answer:
Distance covered by walk = \(\frac{1}{4}\) km
Distance covered by bicycle = \(\frac{3}{4}\) km
Total distance to school from his house = \(\frac{1}{4}\) + \(\frac{3}{4}\)
= \(\frac{1+3}{4}=\frac{4}{4}\) km
Question 14.
a) \(\frac{8}{10}-\frac{2}{10}\) = ………………
b) \(\frac{1}{3}-\frac{1}{9}\) = ………………
c) \(\frac{15}{32}-\frac{3}{8}\) = ………………
d) \(6 \frac{1}{16}-1 \frac{1}{8}\) = ………………
Answer:

![]()
Question 15.
\(\frac{2}{3}\)rd nd part of students in a school is boys. Find the part of girls.
Answer:
Part of boys in a school = \(\frac{2}{3}\)rd
Part of girls inaschool= 1 – \(\frac{2}{3}\).
= \(\frac{3-2}{3}=\frac{1}{3}\)rd.
Question 16.
Subtract \(\frac{21}{4}\) from the total of \(\frac{7}{2}\) and \(\frac{8}{3}\).
Answer:
Total of \(\frac{7}{2}\) and \(\frac{8}{3}\) = \(\frac{7}{2} \times \frac{3}{3}+\frac{8}{3} \times \frac{2}{2}\)
= \(\frac{21}{6}+\frac{16}{6}=\frac{21+16}{6}=\frac{37}{6}\)
Subtract of \(\frac{37}{6}-\frac{21}{4}\) =
LCM of 6 and 4 is 12 = \(\frac{37}{6} \times \frac{2}{2}-\frac{21}{4} \times \frac{3}{3}=\frac{74-63}{12}=\frac{11}{12}\)
Question 17.
Govind studied \(\frac{2}{5}\) th part of a book on 1st day, \(\frac{1}{7}\) th part on 2nd day. Then how much part is yet to be completed?
Answer:
Completed part of book on 1st day = \(\frac{2}{5}\)th
Completed part of book on 2nd day = \(\frac{1}{7}\)th
Completed part of book on two days = \(\frac{2}{5}\) + \(\frac{1}{7}\)
LCM of 5 and 7 is 35.
= \(\frac{2}{5} \times \frac{7}{7}+\frac{1}{7} \times \frac{5}{5}\)
= \(\frac{14}{35}+\frac{5}{35}=\frac{14+5}{35}=\frac{19}{35}\)
remaining part of book yet to be completed = 1 – \(\frac{19}{35}\)
= \(\frac{1 \times 35}{35}-\frac{19}{35} \times \frac{1}{1}\)
= \(\frac{35}{35}-\frac{19}{35}=\frac{35-19}{35}=\frac{14}{35}\)
![]()
Question 18.
Write in words 189.257
Answer:
One hundred and eight nine point two five seven.
Question 19.
Write the place value of 6 ¡n 489.167
Answer:
6 is in \(\frac{1}{100}\)th place.