SCERT AP 6th Class Maths Solutions Chapter 3 గ.సా.కా – క.సా.గు InText Questions and Answers.
AP State Syllabus 6th Class Maths Solutions 3rd Lesson గ.సా.కా – క.సా.గు InText Questions
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 31]
ప్రశ్న 1.
900, 452, 9534, 788 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా ? ఎందుకు ?
సాధన.
900, 452, 9534, 788 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయి. ఎందుకనగా ఇచ్చిన సంఖ్యల ఒకట్ల స్థానంలో వరుసగా 0, 2, 4, 8లు కలవు.
ప్రశ్న 2.
953, 457, 781, 325, 269 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా ? ఎందుకు ?
సాధన.
953,457, 781, 325, 269 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడవు. ఎందుకనగా ఈ సంఖ్యల ఒకట్ల స్థానంలో 0,2,4,6,8 అంకెలు లేవు.
ప్రశ్న 3.
452, 673, 259, 356 సంఖ్యలు 2 చే నిశ్శేషంగా భాగింపబడతాయా? సరిచూడండి.
సాధన.
452, 673, 259, 356 లలో 452 మరియు 356 లు 2 చే నిశ్శేషంగా భాగింపబడతాయి.
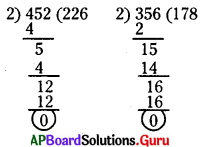
673, 259 లు 2చే నిశ్శేషంగా భాగింపబడవు.
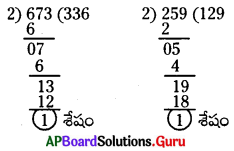
![]()
[పేజి నెం. 32]
కింది సంఖ్యలు 3 చేత భాగించబడతాయో, లేదో చెప్పండి (భాజనీయతా సూత్రం ఉపయోగించి). భాగహారంతో సరిచూడండి.
అ) 123456
ఆ) 61392
ఇ) 8747
సాధన.
అ) 12345
అంకెల మొత్తం = 1 + 2 + 3 + 4 + 5 = 15
15, 3 చే నిశ్శేషంగా భాగించబడును.
కావున 12345, 3చే నిశ్శేషంగా భాగింపబడుతుంది.
సరిచూడడం :

ఆ) 61392
అంకెల మొత్తం = 6 + 1 + 3 + 9 + 2 = 21
21, 3 చే నిశ్శేషంగా భాగింపబడుతుంది.
కావున 61392, 3 చే నిశ్శేషంగా భాగింపబడుతుంది.
సరిచూడడం :

ఇ) 8747
అంకెల మొత్తం = 8 + 7 + 4 + 7 = 26
26, 3 చే నిశ్శేషంగా భాగింపబడదు.
కావున 8747 ను 3 నిశ్శేషంగా భాగించదు.
సరిచూడడం :

![]()
ప్రయత్నించండి [పేజి నెం. 32]
ప్రశ్న 1.
8430 సంఖ్య 6 తో నిశ్శేషంగా భాగింపబడునా ? ఎందుకు?
సాధన.
8430 ని 2 భాగిస్తుంది (ఒకట్ల స్థానంలో ‘0’ కలదు)
అంకెల మొత్తం = 8 + 4 + 3 + 0 = 15
15, 3 చే నిశ్శేషంగా భాగింపబడుతుంది. కావున 8430, 2 మరియు 3 లచే భాగింపబడుతున్నది.
కావున 6 చే కూడా భాగింపబడుతుంది.
ప్రశ్న 2.
ఏవైనా 3 నాలుగంకెల సంఖ్యలను తీసుకొని, అవి 6తో భాగింపబడునో, లేదో సరిచూడండి.
సాధన.
i) 6324, ii) 9314 iii) 7425, iv) 5436 అనే నాలుగు 3 అంకెల సంఖ్యలను తీసుకొందాము.
i) 6324 ను 2 నిశ్శేషంగా భాగిస్తుంది. (ఒకట్ల స్థానం 4 కావున)
6 + 3 + 2 + 4 = 15, 15, 3 చే నిశ్శేషంగా భాగించబడుతుంది.
6324 ను 3 నిశ్శేషంగా భాగిస్తుంది.
6324, 2 మరియు 3చే నిశ్శేషంగా భాగింపబడుతున్నది.
కావున 6 చే భాగింపబడుతుంది.
ii) 9314, 2 చే భాగిస్తుంది. (ఒకట్ల స్థానం 4 కావున)
9 + 3 + 1 + 4 = 17, కావున 3 1 9314 నిశ్శేషంగా భాగింపబడదు.
9314 ను 3 నిశ్శేషంగా భాగింపబడుట లేదు. కావున 6 చే నిశ్శేషంగా భాగింపబడదు.
iii)7425 యొక్క ఒకట్ల స్థానం 5 కావున 7425 ను 2 నిశ్శేషంగా భాగించదు. కావున 6 తో నిశ్శేషంగా భాగింపబడదు.
iv) 5436 యొక్క ఒకట్ల స్థానం 6, అంకెల మొత్తం 5 + 4 + 3 + 6 = 18 కావున 5436 ను 2 మరియు 3లు నిశ్శేషంగా భాగిస్తాయి.
కావున 5436 ను 6 నిశ్శేషంగా భాగిస్తుంది.
ప్రశ్న 3.
6తో భాగింపబడి 2, 3లతో భాగించబడని సంఖ్యకు ఉదాహరణనివ్వగలవా ? ఎందుకు?
సాధన.
6చే భాగింపబడి 2, 3 లతో భాగింపబడని సంఖ్యలకు ఉదాహరణను ఇవ్వలేము.
ఎందుకనగా 6చే భాగింపబడే సంఖ్యలన్నీ 2 మరియు 3లచే భాగింపబడతాయి.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 33]
ప్రశ్న 1.
6669 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుందా ? పరీక్షించండి.
సాధన.
అంకెల మొత్తం = 6 + 6 + 6 + 9 = 27
27, 6 చే నిశ్శేషంగా భాగించబడుతుంది. కావున 6669 సంఖ్య 9చే నిశ్శేషంగా భాగింపబడుతుంది.

ప్రశ్న 2.
భాగహారం చేయకుండానే, 8989794 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుందో, లేదో కనుగొనండి.
సాధన.
ఇచ్చిన సంఖ్యలోని అంకెల మొత్తం = 8 + 9 + 8 + 9 + 7 + 9 + 4 = 54
54 ను 9 నిశ్శేషంగా భాగిస్తుంది. కావున
8989794 సంఖ్య 9 చేత నిశ్శేషంగా భాగింపబడుతుంది.
ప్రశ్న 3.
28570, 90875 సంఖ్యలు 5 చే భాగించబడునా ? భాగహారం చేసి సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్యలు 28570, 90875 సంఖ్యల ఒకట్ల స్థానంలో వరుసగా 0, 5 కలవు కావున ఈ సంఖ్యలు 5 చే నిశ్శేషంగా భాగింపబడతాయి.
సరిచూడటం:

![]()
[పేజి నెం. 34]
ప్రశ్న 4.
598, 864, 4782 మరియు 8976 సంఖ్యలు 4 చేత నిశ్శేషంగా భాగించబడునో, లేదో పరిశీలించండి. భాజనీయతా సూత్రంను ఉపయోగించండి మరియు భాగహారంతో సరిచూడండి.
సాధన.
ఇచ్చిన సంఖ్యలు 598, 864, 4782 మరియు 8976.
i) 598 లో పదుల, ఒకట్ల స్థానంలోని సంఖ్య 98.
98ని నాలుగు నిశ్శేషంగా భాగించడం లేదు.
కావున 5989 4 నిశ్శేషంగా భాగించదు.
సరిచూచుట :

ii) 864 పదుల, ఒకట్ల స్థానంలోని సంఖ్య = 64.
64 ను 4 నిశ్శేషంగా భాగిస్తుంది.
కావున 864 ను 4 నిశ్శేషంగా భాగిస్తుంది.
సరిచూచుట :

iii) 4782
పదుల, ఒకట్ల స్థానంలోని సంఖ్య 82.
82 ను 4 నిశ్శేషంగా భాగించడం లేదు.
కావున 4782 ను 4 నిశ్శేషంగా భాగించదు.
సరిచూచుట :
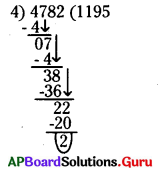
iv) 8976
పదుల, ఒకట్ల స్థానంలోని సంఖ్య 76
76 ను 4 నిశ్శేషంగా భాగిస్తుంది.
కావున 8976 ను 4 నిశ్శేషంగా భాగిస్తుంది.
సరిచూచుట :

[పేజి నెం. 35]
ఖాళీలను పూరించి, పట్టికను పూర్తిచేయండి.
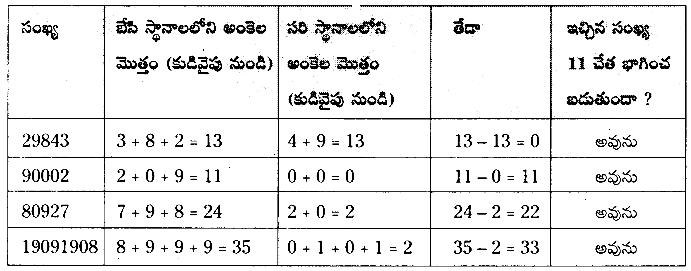
పై పట్టిక నుండి ఏమి గమనించారు ?
సాధన.
ప్రతి సందర్భంలో ఈ తేడా ‘0’ లేదా ’11’ యొక్క గుణిజము.
ఈ సంఖ్యలన్నీ 11చే నిశ్శేషంగా భాగింపబడుతాయి.
![]()
ప్రయత్నించండి [పేజి నెం. 35]
1221 అనేది “ద్విముఖ సంఖ్య” (పాలి డ్రోమ్ సంఖ్య). ద్విముఖ సంఖ్య అనగా కుడినుండి ఎడమవైపు లేదా ఎడమనుండి కుడివైపు మార్చి రాసినా సంఖ్య మారదు. అందుచే ప్రతి సరి అంకెలు గల్గిన ద్విముఖ సంఖ్య, 11 చే నిశ్శేషంగా భాగింపబడుతుంది. 6 అంకెల ద్విముఖ సంఖ్యను రాయండి.
సాధన.
111111, 222222, 333333, 444444, 555555,
112211, 223322, 334433, 441144, 556655,
122221, 221122, 312213, 423324, 589985,
123321, 231132, 345543, 456654, 576675
142241, 234432, 326623, 478874, 598895
ఇవి అన్నీ 6 అంకెల ద్విముఖ సంఖ్యలు.
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 37]
ప్రశ్న 1.
60 యొక్క కారణాంకాలు రాయండి.
సాధన.
60 = 1 × 60
60 = 2 × 30
60 = 3 × 20
60 = 4 × 15
60 = 5 × 12
60 = 6 × 10
∴ 60 యొక్క కారణాంకాలు 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60.
ప్రశ్న 2.
ఒక సంఖ్య యొక్క కారణాంకాలన్నీ ఆ సంఖ్యను నిశ్శేషంగా భాగిస్తాయా ? 30 యొక్క కారణాంకాలను కనుగొనండి. భాగహార పద్ధతి ద్వారా సరిచూడండి.
సాధన.
ఒక సంఖ్య యొక్క కారణాంకాలు అన్నీ ఆ సంఖ్యను నిశ్శేషంగా భాగిస్తాయి.
30 = 1 × 30
30 = 2 × 15
30 = 3 × 10
30 = 5 × 6
30 కారణాంకాలు : 1, 2, 3, 5, 6, 10, 15, 30.
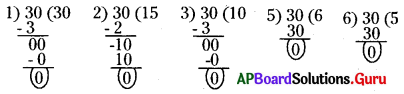
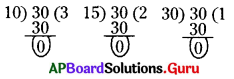
పై భాగహారాలను మనం గమనించినట్లయితే 30 కారణాంకాలైన 1, 2, 3, 5, 6, 10, 15, 30 ల అన్నింటితోను నిశ్శేషంగా భాగింపబడుతున్నది.
ప్రశ్న 3.
15 మరియు 24 యొక్క కారణాంకం 3. ఈ సంఖ్యల భేదానికి కూడా 3 కారణాంకం అవుతుందా?
సాధన.
15 మరియు 24 ల భేదం = 24 – 15 = 9
9 కి 3 కారణాంకం అవుతుంది.
![]()
ప్రయత్నించండి [పేజి నెం. 38]
ప్రశ్న 1.
కనిష్ఠ ప్రధాన సంఖ్య ఏది?
సాధన.
2
ప్రశ్న 2.
కనిష్ఠ సంయుక్త సంఖ్య ఏది?
సాధన.
4
ప్రశ్న 3.
కనిష్ఠ బేసి ప్రధాన సంఖ్య ఏది?
సాధన.
3
ప్రశ్న 4.
కనిష్ఠ బేసి సంయుక్త సంఖ్య ఏది?
సాధన.
9
ప్రశ్న 5.
సరి సంయుక్త, బేసి సంయుక్త సంఖ్యలను పదేసి చొప్పున రాయండి.
సాధన.
సరి సంయుక్త సంఖ్యలు : 4, 6, 8, 10, 12, 14, 16, 18, 20, 22.
బేసి సంయుక్త సంఖ్యలు : 9, 15, 21, 25, 27, 33, 35, 39, 45, 49.
ప్రయత్నించండి [పేజి నెం. 39]
ప్రశ్న 1.
రెండంకెల ఒక ప్రధాన సంఖ్యను తిప్పిరాయగా వచ్చిన సంఖ్య కూడా ప్రధాన సంఖ్యే అవుతుందా? ఊహించండి.
(గమనిక : 2 అంకెల సంఖ్యలను తీసుకొని పరిశీలించండి)
సాధన.
రెండంకెల ఒక ప్రధాన సంఖ్యను తిప్పి రాయగా వచ్చిన సంఖ్య కూడా ప్రధాన సంఖ్య కావచ్చును, కాకపోవచ్చును.
ఉదా: 13 ప్రధాన సంఖ్య, 31 కూడా ప్రధాన సంఖ్య.
23 ప్రధాన సంఖ్య, 32 ప్రధాన సంఖ్య కాదు.
ప్రశ్న 2.
311 ప్రధాన సంఖ్య. దీనిలో అంకెలను తారుమారు చేసి మరో రెండు ప్రధాన సంఖ్యలను కనుగొనండి.
సాధన.
113, 131
![]()
నీ ప్రగతిని సరిచూసుకో [పేజి నెం. 40]
ప్రశ్న 1.
కింద ఇవ్వబడిన సంఖ్యల నుండి సాపేక్ష ప్రధాన సంఖ్యల జతలను గుర్తించండి.
2, 3, 4, 5, 6, 7, 8, 9 మరియు 10.
సాధన.
2, 3, 4, 5, 6, 7, 8, 9 మరియు 10 లలో సాపేక్ష ప్రధాన సంఖ్యల జతలు
(2, 3), (2, 5), (2, 7), (2, 9), (3, 4), (3, 5), (3, 7), (3, 8), (3, 10), (4, 5), (4, 7), (4, 9), (5, 6), (5, 7), (5, 8), (5, 9), (6, 7), (7, 8), (7, 9), (7, 10), (8, 9), (9, 10).
ప్రశ్న 2.
50 కన్నా తక్కువైన కవల ప్రధాన సంఖ్యల జతలను రాయండి.
సాధన.
50 కన్నా తక్కువైన కవల ప్రధానాంకాల జతలు
(3, 5); (5, 7); (11, 13); (17, 19); (29, 31), (41, 43).
[పేజి నెం. 42]
12, 16 మరియు 28 యొక్క గ.సా.భాను కనుగొనండి.
సాధన.
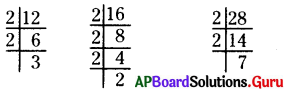
∴ 12 = 2 × 2 × 3
16 = 2 × 2 × 2 × 2
28 = 2 × 2 × 7
12, 16 మరియు 28 ల ఉమ్మడి కారణాంకం = 2 × 2 = 4
కావున, 12, 16 మరియు 28 ల గ.సా.భా = 4.
ప్రయత్నించండి [పేజి నెం. 43]
ఏవైనా రెండు సంఖ్యల గ.సా.భా ఎంత?
అ) వరుస సంఖ్యలు?
ఆ) వరుస సరి సంఖ్యలు?
ఇ) వరుస బేసి సంఖ్యల గ.సా.భా ఏమవుతుంది? మీరేమి గమనించారు? మీ స్నేహితులతో చర్చించండి.
సాధన.
అ) వరుస సంఖ్యల గ.సా.భా = 1
ఆ) వరుస సరి సంఖ్యల గ.సా.భా = 2 .
ఇ) వరుస బేసి సంఖ్యల గ.సా.భా = 1
గమనించిన అంశాలు :
i) ఏవేని రెండు వరుస సంఖ్యల గ.సా.భా ఎల్లప్పుడు 1.
ii) ఏవేని రెండు వరుస సరిసంఖ్యల గ.సా.భా ఎల్లప్పుడు 2.
iii) ఏవేని రెండు వరుస బేసి సంఖ్యల గ.సా.భా ఎల్లప్పుడు 1.
![]()
[పేజి నెం. 45]
ఈ క్రింది వాటి క.సా.గు కనుక్కోండి.
అ) 3, 4
ఆ) 10, 11
ఇ) 10, 30
సాధన.
అ) ఇవ్వబడిన సంఖ్యలు = 3, 4
3 యొక్క కారణాంకాలు = 1 × 3
4 యొక్క కారణాంకాలు = 2 × 2
3, 4 ల యొక్క క.సా.గు = 1 × 3 × 2 × 2 = 12
ఆ) ఇవ్వబడిన సంఖ్యలు = 10, 11
10 యొక్క కారణాంకాలు : 2 × 5
11 యొక్క కారణాంకాలు = 1 × 11
10, 11 ల యొక్క క.సా.గు = 2 × 5 × 11 = 110
ఇ) ఇవ్వబడిన సంఖ్యలు = 10, 30
10 యొక్క కారణాంకాలు = 2 × 5
30 యొక్క కారణాంకాలు = 2 × 3 × 5
10, 30 ల యొక్క క.సా.గు = 2 × 3 × 5 = 30
ఈ) ఇవ్వబడిన సంఖ్యలు = 12, 24
12 యొక్క కారణాంకాలు = 2 × 2 × 3
24 యొక్క కారణాంకాలు = 2 × 2 × 2 × 3
12, 24 ల యొక్క క.సా.గు = 2 × 2 × 2 × 3 = 24
ఉ) ఇవ్వబడిన సంఖ్యలు = 3, 12
3 యొక్క కారణాంకాలు = 1 × 3
12 యొక్క కారణాంకాలు = 2 × 2 × 3
3, 12 ల యొక్క క.సా.గు = 3 × 2 × 2 = 12
[పేజి నెం. 47]
రెండు కవల ప్రధాన సంఖ్యల క.సా.గు మరియు గ.సా.భా ఏమవుతుంది ?
సాధన.
రెండు కవల ప్రధాన సంఖ్యల క.సా.గు మరియు గ.సా.భా = 1
ఉదాహరణలు
ప్రశ్న 1.
6535 సంఖ్య 11 చేత భాగించబడుతుందా ?
సాధన.
బేసి స్థానాలలోని అంకెల మొత్తం = 5 + 5 = 10
సరి స్థానాలలోని అంకెల మొత్తం = 3 + 6 = 9
వాటి తేడా = 10 – 9 = 1
1 సంఖ్య 11 చేత భాగింపబడుతుందా ? కాదు.
కావున, 6535 సంఖ్య 11 చేత భాగించబడదు.
ప్రశ్న 2.
1221 సంఖ్య 11 చేత భాగించబడుతుందా ?
సాధన.
బేసి స్థానాలలోని అంకెల మొత్తం = 1 + 2 = 3
సరి స్థానాలలోని అంకెల మొత్తం = 2 + 1 = 3
వాటి తేడా = 3 – 3 = 0
కావున, 1221 సంఖ్య 11 చేత భాగించబడుతుంది.
ప్రశ్న 3.
100 ను ప్రధాన సంఖ్యల లబ్దంగా రాయండి.
సాధన.
100 = 2 × 50
= 2 × 2 × 25
100 = 2 × 2 × 5 × 5
![]()
ప్రశ్న 4.
32 మరియు 40 యొక్క గ.సా.భాను కనుగొనండి.
సాధన.

‘0’ శేషం వచ్చినపుడు చివరి విభాజకం 8.
∴ 32, 40 ల యొక్క గ.సా.భా = 8.
ప్రశ్న 5.
40, 56 మరియు 60 ల యొక్క గ.సా.భా ను కనుగొనండి.
సాధన.
సోపానం – 1: మొదటగా 40 మరియు 56 ల యొక్క గ.సా.భాను కనుగొనాలి.
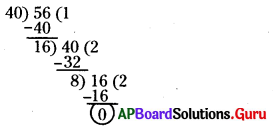
శేషం ‘0’ అయినపుడు చివరి విభాజకం 8.
∴ 40 మరియు 56 యొక్క గ.సా.భా = 8.
సోపానం – 2: ఇప్పుడు మూడవ సంఖ్యతో మొదటి రెండు సంఖ్యల యొక్క గ.సా.భాతో తిరిగి గ.సా.భాను కనుగొనండి.
అంటే 60 మరియు 8 ల యొక్క గ.సా.భాను కనుగొనండి.

శేషం ‘0’ అయినపుడు చివరి విభాజకం 4.
∴ 60 మరియు 8 ల గ.సా.భా = 4
సోపానం – 3: ఇచ్చిన మూడు సంఖ్యల యొక్క గ.సా.భా = 4.
∴ 40, 56 మరియు 60 యొక్క గ.సా.భా 4.
ప్రశ్న 6.
రెండు ట్యాంకర్లలో వరుసగా 850 లీటర్లు మరియు 680 లీటర్ల కిరోసిన్ ఉన్నది. రెండు ట్యాంకర్లలో ఉన్న కిరోసిన్ ను కొలవగలిగే గరిష్ఠ సామర్థ్యం గల కొలపాత్ర యొక్క సామర్థ్యం ఎంత?
సాధన.
రెండు ట్యాంకర్లలో వున్న కిరోసిన్ ను కొలవగలిగే పాత్ర సామర్థ్యం ట్యాంకర్ల సామర్థ్యాన్ని కచ్చితంగా భాగించే విభాజకం కావాలి. ఈ సామర్థ్యం (విభాజకం) గరిష్ఠంగా ఉండాలి. అనగా కొలపాత్ర యొక్క గరిష్ఠ సామర్థ్యం 850, 680 ల యొక్క గ.సా.భా కావాలి. 850, 680 ల యొక్క గ.సా.భా 170.
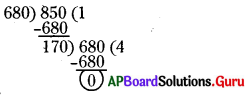
అందుచే రెండు ట్యాంకర్లలోని కిరోసినను కొలవగలిగే పాత్ర యొక్క గరిష్ఠ సామర్థ్యం 170 లీటర్లు. మొదటి ట్యాంకర్ లోని కిరోసినను 5 సార్లు, రెండవ ట్యాంకర్ లోని కిరోసిన్ ను 4 సార్లు కొలవగల్గుతుంది.
ప్రశ్న 7.
21, 35 మరియు 42 ల యొక్క క.సా.గును కనుగొనండి.
సాధన.
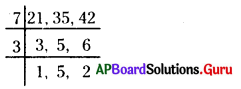
21, 35, 42 ల యొక్క క.సా.గు 7 × 3 × 5 × 2 = 210.
![]()
ప్రశ్న 8.
8 మరియు 12లక.సా.గును కనుగొని, సంబంధాన్ని ఉపయోగించి సంఖ్యల గ.సా.భాను కనుగొనండి.
సాధన.
8 మరియు 12 ల క.సా.గు = 2 × 2 × 2 × 3 = 24
\(\begin{array}{l|ll}
2 & 8, & 12 \\
\hline 2 & 4, & 6 \\
\hline & 2, & 3
\end{array}\)
క.సా.గు × గ.సా.భా = సంఖ్యల లబ్దం అని మనకు తెలుసు
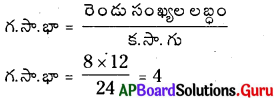
∴ 8 మరియు 12 ల గ.సా.భా = 4