Students can go through AP Board 7th Class Maths Notes Chapter 2 Fractions, Decimals and Rational numbers to understand and remember the concepts easily.
AP State Board Syllabus 7th Class Maths Notes Chapter 2 Fractions, Decimals and Rational numbers
→ A proper fraction is a fraction that represents a part of a whole i.e., a fraction in which numerator is less than the denominator is called a proper fraction.
Eg: \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{2}{3}\), \(\frac{5}{6}\), \(\frac{8}{13}\),….. etc
→ An improper fraction is a fraction that represents a whole or more than a whole i.e., a fraction in which the numerator is more than or equal to the denominator is called an improper fraction.
Eg: \(\frac{5}{3}\), \(\frac{4}{3}\), \(\frac{8}{7}\), \(\frac{11}{5}\), ….. etc
![]()
→ Fractions can be represented pictorially.
Eg:

→ Like fractions can be compared by their numerators.
→ Unlike fractions can be compared by converting them into like fractions.
→ An equivalent fraction of a given fraction can be obtained by multiplying its numerator and denominator by same number.
Eg: Equivalent fraction for \(\frac{3}{5}\) is

→ To multiply a fraction with a whole number; we take the product of the numerator and the whole number as the new numerator, keeping the denominator the same.
Eg:
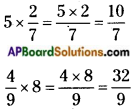
→ Product of the fractions = \(\frac{\text { Product of Numerators }}{\text { Product of Denominators }}\)
Eg: \(\frac{5}{3}\) × \(\frac{4}{7}\) = \(\frac{20}{21}\)
→ In mathematical computation ‘of’ means multiplication.
Eg: \(\frac{1}{3}\) of 24 = \(\frac{1}{3}\) × 24 = 8
![]()
→ The product of two proper fractions is less than each of the fraction in multiplication.
Eg:
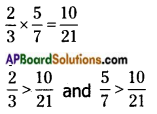
→ The product of a proper and improper fraction is less than the improper fraction and greater than the proper fraction.
Eg: \(\frac{3}{4}\) × \(\frac{7}{5}\) = \(\frac{21}{20}\)
Here \(\frac{3}{4}\) < \(\frac{21}{20}\) and \(\frac{7}{5}\) > \(\frac{21}{20}\)
→ The product of two improper fractions is greater than each of the fractions.
Eg: \(\frac{7}{5}\) × \(\frac{3}{2}\) = \(\frac{21}{20}\)
Here \(\frac{7}{5}\) < \(\frac{21}{10}\) and \(\frac{3}{2}\) < \(\frac{21}{20}\)
→ To divide a whole number with a fraction; multiply the whole number by the reciprocal of the given fraction and vice versa.
Eg:
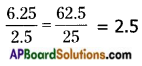
→ To divide one fraction by another, multiply the first fraction with the reciprocal of 2nd fraction.
Eg: \(\frac{3}{5}\) ÷ \(\frac{5}{8}\) = \(\frac{3}{5}\) × \(\frac{8}{5}\)
→ To multiply a decimal by 10,100,1000,, we move the decimal point in the number to the right side as many places as there are zeros in the numbers 10, 100, 1000 ……
Eg:
1.125 × 10 = 11.25
1.125 × 100 = 112.5
1.125 × 1000 = 1125
1.255 × 10,000 = 12,550
→ To multiply two decimal numbers.
i) multiply them as whole numbers.
ii) count the total number of digits in decimal places and add them.
iii) place the decimal point in the product by counting the sum of digits from its right most place.
Eg: 6.25 × 3.14
i) 625 × 314 = 196250
ii) sum of the number of digits in decimal places = 2 + 2 = 4
iii) 19.6250
![]()
→ To divide a decimal number by numbers like 10,100,1000, …… etc. we shift the decimal point in the decimal number to the left by as many places as there are zeros in 10, 100,1000 etc.
Eg: 435.873 ÷ 10 = 43.5873
4551.3 ÷ 100 = 45.513
8374.2 ÷ 1000 = 8.3742
24.82 ÷ 1000 = 0.02482
→ To divide a decimal number by a whole number
i) divide them as whole numbers
ii) place the decimal point in the quotient as in the decimal number.
Eg: 86.5 ÷ 5
i) 865 ÷ 5 = 173
ii) 17.3
To divide a decimal number by another,
i) shift the decimal to the right by equal number of places in both to convert the denominator to a whole number.
ii) divide them as in above
Eg: 6.25 ÷ 2.5
→ The numbers in the form \(\frac{p}{q}\) where p, q are integers and q ≠ 0 are called rational numbers.
→ The set of rational numbers is represented by Q.
→ Q includes all integers, positive fractional numbers and negative fractional numbers.
→ All rational numbers can be represented on a number line.