AP State Syllabus AP Board 7th Class Maths Solutions Chapter 12 Quadrilaterals InText Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 12th Lesson Quadrilaterals InText Questions
![]()
Try This
Question 1.

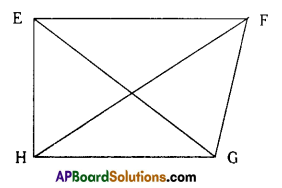
Is quadrilateral EFGH a convex quadrilateral ?
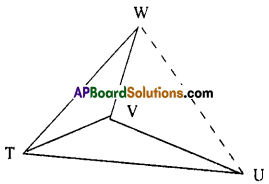
(ii) Is quadrilateral TUVW a concave quadrilateral?
0ii) Draw both the diagonals for quadrilateral EFGH. Do they intersect each other?
(iv) Draw both the diagonals for quadrilateral TUVW. Do they intersect each other?
You will find that the digonals of a convex quadrilateral intersect each other in the interior of the quadrilateral and the diagonals of a concave quadrilateral intersect each other in the exterior of the quadrilateral. (Page No. 229)
Solution:
i) Yes.
ii) Yes.
iii) In □ EFGH, the diagonals intersect each other.
iv) In □ TUVW, the diagonals do not interest each other.
![]()
Question 2.
What would happen if the quadrilateral is not convex ? Consider quadrilateral ABCD. Split it into two triangles and find the sum of the interior angles. What is the sum of interior angles of a concave quadrilateral. (Page No. 230)
Solution:
Sum of the interior angles of a quadrilateral (convex or concave) is always equal to 360°.
Do This
Question 1.
Find the other adjacent sides and common vertices. (Page No. 227)
Solution:
adj. sides — common vertex
\(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\) – – B
\(\overline{\mathrm{BC}}, \overline{\mathrm{CD}}\) – – C
\(\overline{\mathrm{CD}}, \overline{\mathrm{DA}}\) – – D
AB, AD — A
Question 2.
Find the other pairs of adjacent angles and sides. (Page No. 227)
adj. angles — side
∠A, ∠B — AB
∠B, ∠C – – BC
∠C, ∠D – – CD
∠D, ∠A – – DA
![]()
Try This
Question 1.
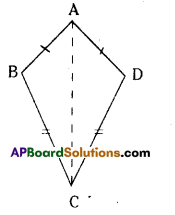
Prove that in a kite ABCD, ΔABC, and ΔADC are congruent. (Page No. 223)
Solution:
Proof in ΔABC and ΔADC,
AB = AD (consecutive sides of the kite)
BC = DC (consecutive sides of the kite)
AC = AC (common side)
∴ By S.S.S congruency criterion ,
ΔABC ∦ ΔADC
Do This
Question 1.
Identify two more pairs of supplementary angles from the parallelogram ABCD given. (Page No. 236)
Solution:
In parallelogram ABCD, the pairs of supplementary angles are
(∠A, ∠B), (∠B, ∠C), (∠C, ∠D) and (∠D, ∠A)

Try This
Question 1.
How many different quadrilaterals can be obtained from the adjacent figure ? Name them. (Page No. 228)
Solution:
Nine quadrilaterals can be obtained.
Quadrilateral ABCD ABDE ACDE,
AHDE BCDE, CDEG,
DFGH, BCDF, DEGH
![]()
Question 2.
From example 7 given in text book (Page No – 237) can you find m ∠I and m∠G by any other method. (Page No. 237)
Solution:
As ∠R = ∠N = 70° and ∠I = ∠G = x° say
∠R + ∠I + ∠N + ∠G = 360°
70° + x° + 70° + x° = 360°
2x = 360° – 140° = 220°