SCERT AP 7th Class Maths Solutions Pdf Chapter 3 సామాన్య సమీకరణాలు Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson సామాన్య సమీకరణాలు Unit Exercise
ప్రశ్న 1.
సరియైన జవాబుని ఎంచుకోండి.
(i) క్రింది వాటిలో ఏ విలువ సమీకరణాన్ని సంతృప్తి పరుస్తుంది – 6+ m = – 10?
(ఎ) 2
(బి) 4
(సి) 4
(డి) 2
సాధన.
(సి) 4
వివరణ:
– 6+ m = – 10
∴ m = – 10 + 6 = -4
![]()
(ii) క్రింది ఏ సమీకరణానికి సాధన ‘-2 ‘ అవుతుంది ?
(ఎ) x + 2 = 5
(బి) 7 + 3x = 1 .
(సి) 2x + 3 = 7
(డి) 2(x + 1) = 4
సాధన.
(బి) 7 + 3x = 1
వివరణ:
x = – 2 ను ఇచ్చిన అన్ని సమీకరణాలలో ప్రతిక్షేపించగా,
(ఎ) LHS = – 2 + 2 = 0 ≠ RHS
(బి) LHS = 7 + 3(-2) = 7 – 6 = 1 = RHS
LHS = RHS
(సి) LHS = 2(-2) + 3 = – 4 + 3 = – 1 ≠ RHS
(డి) LHS = 2(-2 + 1) = 2(- 1) = – 2 ≠ RHS
(iii) a మరియు bలు ధన పూర్ణాంకాలు అయితే, ax = b సమీకరణం యొక్క సాధన ఎల్లప్పుడూ ఒక
(ఎ) ధన సంఖ్య
(బి) రుణ సంఖ్య
(సి) 1
(డి) 0
సాధన.
(ఎ) ధన సంఖ్య
వివరణ:
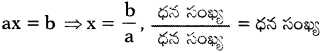
(iv) పూర్ణాంకాలలో సాధనలేని సమీకరణం
(ఎ) 2(x + 3) = 10
(బి) \(\frac{x}{3}\) = 5
(సి) 5 – 3m = 1
(డి) 2k + 1 = 1
సాధన.
(సి) 5 – 3m = 1
(ఎ) 2(x – 3) = 10
⇒ 2x – 6 = 10
⇒ 2x = 10 + 6 = 16
x = \(\frac{16}{2}\) = 8 పూర్ణాంకము.
(బి) \(\frac{x}{3}\) = 5
x = 5 × 3 = 15 పూర్ణాంకము.
(సి) 5 – 3m =1
⇒ – 3m = – 4
m = \(\frac{-4}{-3}\) = \(\frac{4}{3}\) పూర్ణాంకము కాదు.
![]()
(డి) 2k + 1 = 1
2k = 1 – 1 = 0
∴ k = 0 పూర్ణాంకము.
v) ఇచ్చిన సమీకరణంలో కింది వాటిలో ఏది అనుమతించ బడదు ?
(ఎ) సమీకరణం యొక్క రెండు వైపులా ఒకే సంఖ్యను కలుపడం.
(బి) సమీకరణం యొక్క రెండు వైపుల నుండి ఒకే సంఖ్యను తీసివేయడం.
(సి) సమీకరణం యొక్క రెండు వైపులా సున్నా కాని సంఖ్యతో గుణించడం.
(డి) సమీకరణం యొక్క రెండు వైపులా ఒకే సంఖ్యతో భాగించడం.
సాధన.
(డి) సమీకరణం యొక్క రెండు వైపులా ఒకే సంఖ్యతో భాగించడం.
ప్రశ్న 2.
ఖాళీలను పూరించండి.
(i) 2y – 1 = 5 అయితే, 5y + 3 విలువ ___________
సాదన.
2y – 1 = 5
⇒ 2y = 5 + 1 = 6
⇒ y = \(\frac{6}{2}\) = 3
కావున, 5y + 3 = 5(3) + 3
= 15 + 3 = 18
(ii) సమీకరణంలో ఒక వైపు ఉన్న పదాన్ని మరొక వైపుకు మార్చడాన్ని ___________ అంటారు.
సాదన.
పక్షాంతరం
(iii) రెండు సంఖ్యల మొత్తం 60. ఒక సంఖ్య మరొక దానికి మూడు రెట్లు అయిన ఏర్పడు సమీకరణం ____________ .
సాధన.
ఒక సంఖ్య X అనుకొంటే
x + 3x = 60
∴ 4x = 60
(iv) ‘X’ సహజ సంఖ్య అయితే, X – 8 = -8కు సాధన ________________ .
సాధన.
సాధన లేదు. X – 8 = – 8
X = – 8 + 8
= 0 సహజ సంఖ్య కాదు.
(v) సంఖ్య యొక్క రెండు రెట్లు నుండి 13 తీసివేస్తే 3 వస్తుంది అయిన ఆ సంఖ్య, _____________ .
సాధన.
ఒక సంఖ్య X అనుకొంటే
⇒ 2x – 13 = 3
⇒ 2x = 3 + 13 = 16
∴ x = 8
![]()
ప్రశ్న 3.
బ్రాకెట్లలో ఇచ్చిన విలువ ఇచ్చిన సమీకరణానికి సాధనా, కాదా సరిచూడండి.
(ఎ) 2n + 5 = 19 (n = 7)
సాధన.
n = 7ను ఇచ్చిన సమీకరణం 2n + 5 = 19 లో ప్రతిక్షేపించగా,
LHS = 2n + 5
= 2(7) + 5
= 14 + 5 = 19 = RHS
LHS = RHS
కావున, 2n + 5 = 19 నకు n = 7 సాధన అవుతుంది.
(బి) \(\frac{3 \mathrm{~m}}{5}\) – 7 = 1 (m = 10)
సాధన.
m = 10 ని ఇచ్చిన సమీకరణం \(\frac{3 \mathrm{~m}}{5}\) – 7 = 1 నందు ప్రతిక్షేపించగా
LHS = \(\frac{3 \mathrm{~m}}{5}\) – 7
= \(\frac{3(10)}{5}\) – 7
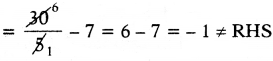
LHS ≠ RHS.
కావున, \(\frac{3 \mathrm{~m}}{5}\) – 7 నకు m = 10 సాధన కాదు.
ప్రశ్న 4.
5 – 2k = – 3 ను యత్న దోష పద్ధతి ద్వారా సాధన కనుగొనండి.
సాధన.
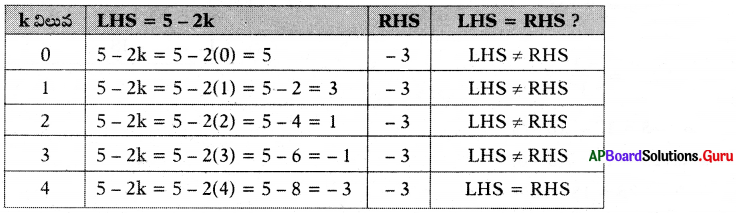
k= 4 అయినపుడు, LHS = RHS అవుతున్నది. కావున, 5 – 2k = – 3 యొక్క సాధన k = 4.
ప్రశ్న 5.
సామాన్య సమీకరణాలను గణిత ప్రవచనాలుగా వ్రాయండి.
(ఎ) 2m + 7 = 21
సాధన.
ఒక సంఖ్య యొక్క రెట్టింపునకు 7 కలిపిన 21 వచ్చును.
(బి) \(\frac{n}{7}\) = 4
సాధన.
ఒక సంఖ్యలో 7 వ వంతు 4.
![]()
ప్రశ్న 6.
క్రింది సమీకరణాలలో చరరాశిని వేరు చేసి సాధించు సందర్భంలో సోపానాలను వ్రాయండి మరియు సాధించండి.
(ఎ) 7(x – 3) = 28
సాధన.
7(x – 3) = 28
7x – 21 = 28 (విభాగ ధర్మం )

(బి) 8y – 9 = 15
సాధన.
8y – 9 = 15

ప్రశ్న 7.
క్రింది సమీకరణాలను సాధించి, సాధనను సరిచూడండి (పక్షాంతరం పద్దతి).
(a) 9(a + 3) + 7 = 22
సాధన.
9(a + 3) + 7 = 22
⇒ 9a + 27 + 7 = 22
⇒ 9a + 34 = 22
34 ను పక్షాంతరం చేయగా
⇒ 9a = 22 – 34
⇒ 9a = – 12
9 ని పక్షాంతరం చేయగా
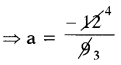
∴ a = \(\frac{-4}{3}\)
సరిచూచుట: a = \(\frac{-4}{3}\) ని ప్రతిక్షేపించగా
LHS = 9(a + 3) +7
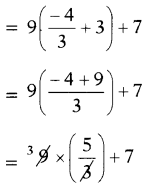
= 15 + 7 = 22 = RHS
∴ LHS = RHS
![]()
(b) 25 = 18 – 7(b-6)
సాధన.
25 = 18 – 7(b – 6)
25 = 18 – 7b + 42
25 = 60 – 7b
– 7b ని పక్షాంతరం చేయగా
25 + 7b = 60
25 ను పక్షాంతరం చేయగా
7b = 60 – 25
7b = 35
7 ను పక్షాంతరం చేయగా
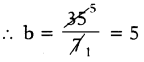
సరిచూచుట: b = 5 ను ఇచ్చిన సమీకరణం నందు ప్రతిక్షేపించగా
RHS = 18 – 7(b – 6)
= 18 – 7(5 – 6)
= 18 – 7(- 1)
= 18 + 7 = 25 = LHS
LHS = RHS
ప్రశ్న 8.
ఒక సంఖ్యకు 6 రెట్లు 72 అయిన ఆ సంఖ్యను కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొందాము
ఒక సంఖ్యకు 6 రెట్లు = 72
⇒ 6x = 72
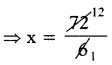
⇒ x = 12
∴ కావలసిన సంఖ్య = 4.
ప్రశ్న 9.
ఒక సంఖ్య యొక్క \(\frac{3}{4}\) వంతు, దాని \(\frac{1}{4}\) వంతు కంటే 2 ఎక్కువ అయిన ఆ సంఖ్య ?
సాధన.
ఒక సంఖ్య = x అనుకొందాము.
ఆ సంఖ్యలో \(\frac{3}{4}\) వ వంతు = \(\frac{3}{4}\) × x = \(\frac{3 x}{4}\)
ఆ సంఖ్యలో \(\frac{1}{4}\) వ వంతు = \(\frac{1}{4}\) × x = \(\frac{x}{4}\)
ఒక సంఖ్యలో \(\frac{3}{4}\) వంతు దాని \(\frac{1}{4}\) వ వంతు కంటే 2 ఎక్కువ
⇒ \(\frac{3 x}{4}\) = \(\frac{x}{4}\) + 2
⇒ \(\frac{3 x}{4}\) – \(\frac{x}{4}\) = 2
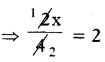
⇒ \(\frac{x}{2}\) = 2
⇒ x = 2 × 2 = 4
∴ కావలసిన సంఖ్య x = 4
![]()
ప్రశ్న 10.
క్రింది పటము చతురస్రం యొక్క చుట్టుకొలత 40 మీ. అయిన X విలువను కనుగొనండి.
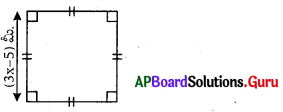
సాధన.
చతురస్రం చుట్టుకొలత 40 మీ.
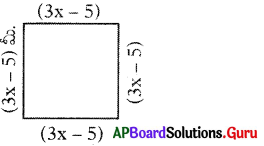
(3x – 5)
చతురస్ర చుట్టుకొలత
⇒ (3x – 5) + (3x – 5) + (3x – 5) + (3x – 5) = 40
⇒ 12x – 20 = 40
⇒ 12x = 40 + 20
⇒ 12x = 60
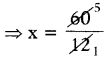
∴ x = 5
(లేదా).
చతురస్ర చుట్టుకొలత = 4 × భుజము
∴ 4(3x – 5) = 40
⇒ 12x – 20 = 40
⇒ 12x = 40 + 20
⇒ 12x = 60
∴ x = \(\frac{60}{12}\) = 5
ప్రశ్న 11.
జీవన్ వయస్సు తన అన్నయ్య శశి, వయస్సు కంటే 3 సంవత్సరాలు తక్కువ. వారి ప్రస్తుత వయస్సుల మొత్తం 19 అయిన ఇద్దరి వయస్సులు ఎంత ?
సాధన.
శశి వయస్సు = x సంవత్సరాలు అనుకొందాము.
కావున, జీవన్ వయస్సు = (x – 3) సంవత్సరాలు ప్రస్తుత వారి వయస్సుల మొత్తం = 19
⇒ x + (x – 3) = 19
⇒ 2x – 3 = 19
⇒ 2x = 19 + 3
⇒ 2x = 22
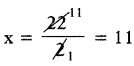
∴ శశి వయస్సు x = 11 సంవత్సరాలు
జీవన్ వయస్సు = x = 3
= 11 – 3 = 8 సంవత్సరాలు
సరిచూచుట:
11 + 8 = 19
![]()
ప్రశ్న 12.
దీర్ఘచతురస్రం యొక్క పొడవు, దాని వెడల్పు కంటే 20 మీ. ఎక్కువ. దీర్ఘచతురస్రం యొక్క చుట్టుకొలత 100 మీ. అయిన దాని యొక్క పొడవు మరియు వెడల్పులను కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర వెడల్పు = x మీ. అనుకొందాము.
∴ పొడవు = (x + 20) మీ.
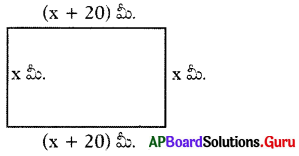
∴ దీర్ఘచతురస్ర చుట్టుకొలత 100 మీ.
⇒ x + (x + 20) + x + (x + 20) = 100
⇒ 4x + 40 = 100
⇒ 4x = 100 – 40
⇒ 4x = 60
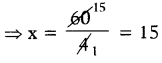
∴ వెడల్పు x = 15 మీ.
పొడవు = x + 20
= 15 + 20 = 35 మీ.
(లేదా)
దీర్ఘచతురస్రం చుట్టుకొలత = 2(పొడవు + వెడల్పు)
⇒ 2[x + (x + 20)] = 100
⇒ 2[2x + 20] = 100
⇒ 4x + 40 = 100
⇒ 4x = 100 – 40 = 60
∴ x = \(\frac{60}{4}\) = 15 మీ.
ప్రశ్న 13.
ఒక కుటుంబంలో, బియ్యం వినియోగం గోధుమ కంటే 4 రెట్లు ఎక్కువ. ఒక నెలలో రెండు తృణధాన్యాలు మొత్తం వినియోగం 30 కిలోలు. కుటుంబంలో వినియోగించే బియ్యం మరియు గోధుమల పరిమాణాలను కనుగొనండి.
సాధన.
కుటుంబంలో ఒక నెల గోధుమ వినియోగం = X కిలోలు అనుకొందాం.
∴ బియ్యం వినియోగం = 45 కిలోలు
కుటుంబంలో ఒక నెలలో రెండు తృణధాన్యాల మొత్తం వినియోగం = 30 కిలోలు
∴ x + 4x = 30
⇒ 5x = 30
⇒ x = \(\frac{30}{5}\) = 6 కిలోలు
∴ గోధుమల వినియోగం X = 6 కిలోలు
బియ్యం వినియోగం = 4x = 4(6) = 24 కిలోలు.
సరిచూచుట:
6 + 24 = 30
ప్రశ్న 14.
ఒక టీచర్ విద్యార్థులతో “ఈ తరగతిలో గరిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు, కనిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కుల రెట్టింపు కంటే 7 ఎక్కువ”. తరగతిలో గరిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు 93 అయినకనిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు ఎంత ?
సాధన.
తరగతిలో కనిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు = x అనుకొందాము.
∴ గరిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు = 2x + 7
(∵ గరిష్ఠ మార్కులు కనిష్ఠ మార్కుల రెట్టింపు కంటే 7 ఎక్కువ)
గరిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు = 93
⇒ 2x + 7 = 93
⇒ 2x = 93 – 7
⇒ 2x = 86
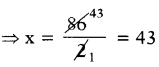
∴ కనిష్ఠ మార్కులు వచ్చిన విద్యార్థి మార్కులు = 43
![]()
ప్రశ్న 15.
ఒక వ్యక్తి తన ప్రయాణం మొత్తంలో \(\frac{4}{5}\) వ వంతు రైలులో, \(\frac{1}{7}\) బస్సులో, మిగిలిన 16 కి.మీ. ఆటో ద్వారా ప్రయాణించాడు. అతని ప్రయాణం యొక్క మొత్తం దూరం ఎంత ?
సాధన.
ఒక వ్యక్తి యొక్క మొత్తం ప్రయాణ దూరం = x కి.మీ. అనుకొనుము.
అతను రైలులో ప్రయాణించిన దూరం
= \(\frac{4}{5}\) × x = \(\frac{4 x}{5}\) కి.మీ.
బస్సులో ప్రయాణించిన దూరం
= \(\frac{1}{7}\) × x = \(\frac{x}{7}\) కి.మీ.
∴ రైలు మరియు బస్సులో ప్రయాణించిన మొత్తం
దూరం = \(\frac{4 x}{5}+\frac{x}{7}\)
5, 7, ల క.సా.గు = 35
= \(\frac{28 x}{35}+\frac{5 x}{35}\)
= \(\frac{33 x}{35}\) కి.మీ.
ఆటోలో ప్రయాణించిన దూరం 16 కి.మీ.
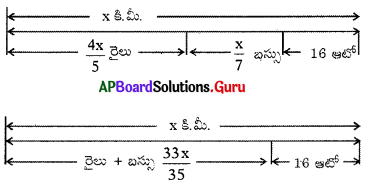

⇒ x = 280 కి.మీ.
∴ వ్యక్తి ప్రయాణించిన మొత్తం దూరం = 280 కి.మీ.