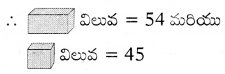SCERT AP 7th Class Maths Solutions Pdf Chapter 3 సామాన్య సమీకరణాలు Ex 3.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 3rd Lesson సామాన్య సమీకరణాలు Exercise 3.4
ప్రశ్న 1.
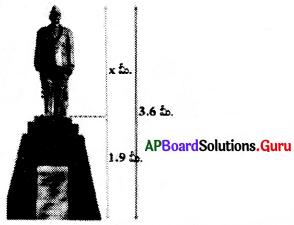
క్రింది పటములో విగ్రహం యొక్క ఎత్తు ఎంత ?
సాధన.
పటం నుండి,
x + 1.9 = 3.6
x = 3.6 – 1.9
x = 1.7 మీ.
![]()
ప్రశ్న 2.
ఒక సంఖ్య యొక్క రెండు రెట్లకు 4 కలిపిన 80 అయిన ఆ సంఖ్య కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొందాము.
ఒక సంఖ్య యొక్క రెండు రెట్లకు 4 కలిపిన 80
⇒ 2x + 4 = 80
⇒ 2x = 80 – 4
⇒ 2x = 76
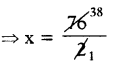
⇒ x = 38
∴ కావలసిన సంఖ్య x = 38
సరిచూచుట:
38 కి రెట్టింపు
= 38 × 2 = 76
= 76 + 4 = 80
ప్రశ్న 3.
ఒక సంఖ్య మరియు ఆ సంఖ్యలో నాల్గవ వంతుల భేదం 24 అయిన ఆ సంఖ్య కనుగొనుము.
సాధన.
ఒక సంఖ్య = x అనుకొందాము.
ఒక సంఖ్య మరియు ఆ సంఖ్యలో నాల్గవ వంతుల భేదం 24.
⇒ x – \(\frac{x}{4}\) = 24
⇒ \(\frac{4 x}{4}\) – \(\frac{x}{4}\) = 24
⇒ \(\frac{3 x}{4}\) = 24
⇒ 3x = 24 × 4
⇒ 3x = 96
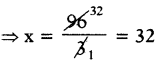
∴ కావలసిన సంఖ్య x = 32
సరిచూచుట:
ఒక సంఖ్య
x = 32
xలో 4వ వంతు
= \(\frac{32}{4}\) = 8
32 – 8 = 24
ప్రశ్న 4.
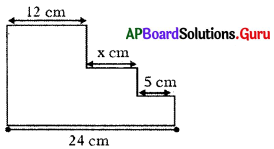
పై పటములో X విలువను కనుగొనుము.
సాధన.
పటం నుండి,
⇒ 12 + x + 5 = 24
⇒ x + 17 = 24
⇒ x = 24 – 11
∴ x = 7 సెం.మీ.
![]()
ప్రశ్న 5.
ఫారన్ హీట్ ఉష్ణోగ్రతమానం నుండి సెంటీ గ్రేడ్ మానంలో ఉష్ణోగ్రతను మార్చడానికి (F – 32) = \(\frac{9}{5}\) × C అనే సూత్రం ఉపయోగిస్తాం. C = – 40°C అయిన F ను కనుగొనండి.
సాధన.
(F – 32) = \(\frac{9}{5}\) × C, C = – 40°C అయిన
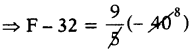
⇒ F – 32 = – 72
⇒ F = – 72 + 32
⇒ F = – 40°
ప్రశ్న 6.
రహీం వద్ద ₹x కలవు అందులో నుండి ₹6 ఖర్చు చేసిన మిగిలిన దానికి రెట్టింపు₹86 అయిన ‘X’ విలువ కనుక్కోండి.
సాధన.
రహీం వద్ద గల ₹xనుండి ₹6 ఖర్చు చేయగా మిగిలినది = ₹(x – 6)
మిగిలిన దానికి రెట్టింపు = ₹86
⇒ 2(x – 6) = 86
⇒ 25 – 12 = 86
⇒ 2x = 86 + 12
⇒ 2x = 98
⇒ x = \(\frac{98}{2}\) = 49
∴ రహీం వద్ద గల డబ్బు X = ₹49.
సరిచూచుట:
రహీం వద్ద గల ₹49లో ₹6 ఖర్చు చేయగా మిగిలినది.
= 49 – 6 = 43
43 × 2 = 86
![]()
ప్రశ్న 7.
రెండు సంఖ్యల మధ్య భేదం 7. చిన్న సంఖ్య ఆరు రెట్లుకు పెద్ద సంఖ్యను కలుపగా మొత్తం 77 అయిన ఆ సంఖ్యలను కనుగొనండి.
సాధన.
చిన్న సంఖ్య = x అనుకొనుము
పెద్ద సంఖ్య = x + 7 (∵ రెండు సంఖ్యల భేదం 7)
చిన్న సంఖ్య ఆరు రెట్లుకు పెద్ద సంఖ్యను కలుపగా మొత్తం = 77
⇒ 6x + (x + 7) = 77
⇒ 7x + 7 = 77
⇒ 7x = 77 – 7
⇒ 7x = 70
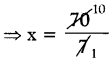
⇒ x = 10
∴ చిన్న సంఖ్య x = 10
పెద్ద సంఖ్య = x + 7 = 10 + 7 = 17
∴ కావలసిన సంఖ్యలు 10 మరియు 17.
సరిచూచుట:
చిన్న సంఖ్యకు 6 రెట్లు
= 6 × 10 = 60
= 60 + 10 = 77
ప్రశ్న 8.
మూడు వరుస సరి సంఖ్యల మొత్తం 54 అయిన ఆ సంఖ్యలను కనుగొనండి.
సాధన.
మూడు వరుస సరిసంఖ్యలలో
చిన్న సరి సంఖ్య = x అనుకొనుము.
= x + 2 మరియు x + 4
మూడు వరుస సరి సంఖ్యల మొత్తం = 54
⇒ x + (x + 2) + (x + 4) = 54
⇒ 3x + 6 = 54
⇒ 3x = 54 – 6
⇒ 3x = 48
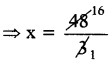
⇒ x = 16
చిన్న సరి సంఖ్య x = 16
కావున, కావలసిన మూడు వరుస సరి సంఖ్యలు = 16, 18, 20.
(లేదా)
వరుస సరిసంఖ్యలలో
రెండవ సరి సంఖ్య = x అనుకొనుము.
1వ సరి సంఖ్య (చిన్న సరిసంఖ్య) = x – 2
3వ సరిసంఖ్య (పెద్ద సరిసంఖ్య) = x + 2
మూడు వరుస సరి సంఖ్యల మొత్తం = 54
![]()
⇒ 3x = 54
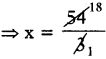
⇒ x = 18
1వ సరి సంఖ్య = x – 2 = 18 – 2 = 16
3వ సరి సంఖ్య = x + 2 = 18 + 2 = 20
∴ కావున కావలసిన మూడు వరుస సరి సంఖ్యలు = 16, 18, 20.
![]()
సరిచూచుట:
16 + 18 + 20 = 54
ప్రశ్న 9.
48 విద్యార్థులు గల తరగతిలో బాలికల సంఖ్య బాలుర సంఖ్యలో మూడవ వంతు.. అయిన ఆ తరగతిలో గల బాలుర సంఖ్య మరియు బాలికల సంఖ్యను కనుక్కోండి. మిగిలిన రెండు సరి సంఖ్యలు
సాధన.
తరగతిలోని బాలుర సంఖ్య = x అనుకొందాము.
తరగతిలోని బాలికల సంఖ్య = \(\frac{x}{3}\)
(∵ బాలికల సంఖ్య, బాలుర సంఖ్యలో 3వ వంతు)
తరగతిలోని విద్యార్థుల సంఖ్య = 48
⇒ x + \(\frac{x}{3}\) = 48
⇒ \(\frac{3 x}{3}\) + \(\frac{x}{3}\) = 48
⇒ \(\frac{4 x}{3}\) = 48
⇒ 4x = 48 × 3.
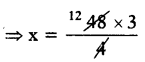
⇒ x = 36
∴ బాలుర సంఖ్య x = 36
బాలికల సంఖ్య \(\frac{x}{3}\) = \(\frac{36}{3}\) = 12
బాలురు = 36 మరియు బాలికలు = 12
ప్రశ్న 10.
మేరీ మరియు జోసెఫ్ యొక్క ప్రస్తుత వయస్సులు 5 : 3 నిష్పత్తిలో ఉన్నాయి. 3 సంవత్సరాల తరువాత వారి వయస్సుల మొత్తం 38. అయిన వారి ప్రస్తుత వయస్సులను కనుగొనండి.
సాధన.
మేరి మరియు జోసెఫ్ యొక్క ప్రస్తుత వయస్సుల నిష్పత్తి
మేరి ప్రస్తుత వయస్సు = 5x
జోసెఫ్ ప్రస్తుత వయస్సు = 3x అనుకొందాం
3 సంవత్సరాల తరువాత
మేరి వయస్సు = 5x + 3
జోసెఫ్ వయస్సు = 3x + 3
3 సంవత్సరాల తరువాత వారి వయస్సుల మొత్తం = 38
⇒ (5x + 3) + (3x + 3) = 38
⇒ 5x + 3 + 3x + 3 = 38
⇒ 8x + 6 = 38
⇒ 8x = 38 – 6
⇒ 8x = 32
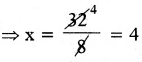
∴ మేరి ప్రస్తుత వయస్సు 5x = 5(4) = 20
జోసెఫ్ ప్రస్తుత వయస్సు 3x = 3(4) = 12
∴ ప్రస్తుత వారి వయస్సులు 20 మరియు 12.
సరిచూచుట:
3 సంవత్సరాల తరువాత వారి వయస్సు
20 + 3 = 23
12 + 3 = 15
మొత్తం = 38
![]()
ప్రశ్న 11.
₹500 మొత్తం ₹5 మరియు ₹ 10 నోట్లలో కలవు మొత్తం నోట్ల సంఖ్య 90 అయిన ఒక్కొక్క రకం నోట్ల సంఖ్యను కనుగొనండి.

సాధన.
₹ 5 నోట్ల సంఖ్య = x అనుకొందాము
₹10 నోట్ల సంఖ్య = 90 – x (∵ మొత్తం నోట్లు 90)
₹5 నోట్ల విలువ = ₹5 × x = 5x
₹10 నోట్ల విలువ = ₹10 × (90 – x)
= 900 – 10x
నోట్ల మొత్తం విలువ = ₹500
⇒ 5x + 900 – 10x = 500
⇒ 900 – 5x = 500
⇒ – 5x = 500 – 900
⇒ – 5x = – 400
⇒ 5x = 400
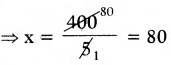
∴ ₹5 నోట్ల సంఖ్య x = 80
₹10 నోట్ల సంఖ్య 90 – x = 90 – 80 = 10.
సరిచూచుట:
₹5 నోట్లు + = 5:3
₹10 నోట్లు
= 80 + 10
= 90
ప్రశ్న 12.
జాన్ మరియు ఇస్మాయిల్ కొంత డబ్బును రిలీఫ్ ఫండక్కు విరాళంగా ఇచ్చారు. ఇస్మాయిల్ చెల్లించిన మొత్తం, జాన్ చెల్లించిన మొత్తానికి రెండు రెట్లు కంటే ₹85 ఎక్కువ. వారు చెల్లించిన మొత్తం డబ్బు ₹4000 అయితే జాన్ విరాళంగా ఇచ్చిన డబ్బును కనుగొనండి.
సాధన.
జాన్ రిలీఫ్ ఫండకు విరాళంగా ఇచ్చిన డబ్బు = ₹x అనుకొనుము.
ఇస్మాయిల్ విరాళంగా చెల్లించిన డబ్బు = ₹(2x + 85)
(∵ ఇస్మాయిల్ చెల్లించిన మొత్తం, జాన్ చెల్లించిన . మొత్తానికి రెట్టింపు కన్నా ₹85 ఎక్కువ)
వారిద్దరూ చెల్లించిన మొత్తం డబ్బు = ₹4000
⇒ x + (2x + 85) = 4000
⇒ 3x + 85 = 4000
⇒ 3x = 4000 – 85
⇒ 3x = 3915
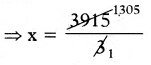
⇒ x = 1305
∴జాన్ విరాళంగా ఇచ్చిన డబ్బు = x = ₹1305
సరిచూచుట:
జాన్ ‘విరాళం = ₹1305 ఇస్మాయిల్ విరాళం
2 × 1305 + 85 = 2695
మొత్తం = ₹4000
![]()
ప్రశ్న 13.
దీర్ఘచతురస్రం యొక్క పొడవు, దాని వెడల్పు 3 రెట్లు కంటే 4 తక్కువ. దీర్ఘచతురస్ర చుట్టుకొలత 32 మీ. అయిన పొడవు, వెడల్పులను కనుగొనండి.
సాధన.
దీర్ఘచతురస్ర వెడల్పు = x మీ.
పొడవు = 3x – 4
(∵ పొడవు, వెడల్పు 3 రెట్లు కంటే 4 తక్కువ)
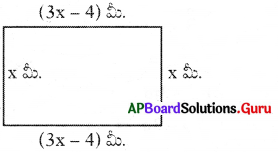
దీర్ఘచతురస్ర చుట్టుకొలత 32 మీ.
⇒ x + (3x – 4) + x + (3x – 4) = 32
⇒ 8x – 8 = 32
⇒ 8x = 32 + 8
⇒ 8x = 40
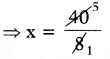
∴ దీర్ఘచతురస్ర వెడల్పు x = 5 మీ.
దీర్ఘచతురస్ర పొడవు 3x – 4
= 3(5) – 4 = 15 – 4 = 11 మీ.
సరిచూచుట:
దీర్ఘచతురస్ర చుట్టుకొలత
= 5 + 11 + 5 + 11
= 32 మీ.
ప్రశ్న 14.
ఒక సంచిలో కొన్ని తెల్ల బంతులు కలవు. తెల బంతులకు రెట్టింపు నీలం బంతులు కలవు. నీలం బంతులకు మూడు రెట్లు ఎర్ర బంతులు కలవు. మొత్తం బంతుల సంఖ్య 27 అయిన ఒక్కొక్క రంగు బంతులు సంచిలో ఎన్ని కలవో లెక్కించండి.
సాధన.
సంచిలోని తెల్ల బంతుల సంఖ్య = x అనుకొనుము
నీలం బంతుల సంఖ్య = 2x
ఎర్ర బంతుల సంఖ్య = 3(2x) = 6x
సంచిలోని మొత్తం బంతుల సంఖ్య = 27
⇒ x + 2x + 6x = 27
⇒ 9x = 27
⇒ x = \(\frac{27}{9}\) = 3
తెల్ల బంతుల సంఖ్య x = 3.
నీలం బంతుల సంఖ్య = 2x = 2(3) = 6
ఎర్ర బంతుల సంఖ్య = 6x = 6(3) = 18
ప్రశ్న 15.

(i)
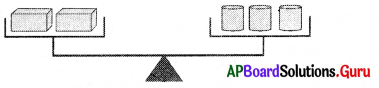
సాధన.
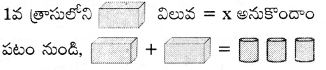
x + x = 36 + 36 + 36
2x = 3 × 36
2x = 108
x = \(\frac{108}{2}\) = 54
![]()
![]()
(ii)
సాధన.
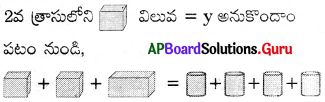
y + y + 54 = 36 + 36 + 36 + 36
2y + 54 = 4 × 36
2y + 54 = 144
2y = 144 – 54
2y = 90
y = \(\frac{90}{2}\) = 45