SCERT AP 7th Class Maths Solutions Pdf Chapter 4 Lines and Angles Ex 4.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 4th Lesson Lines and Angles Exercise 4.4
Question 1.
In the given figure, two lines p ∥ q and r are transversal, If ∠3 = 135°, then find the remaining angles.
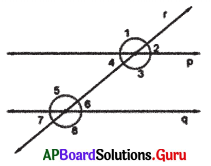
Answer:
Given ∠3 = 135
∠1 = ∠3 = 135° (vertically opposite angles)
∠1 = ∠5 = 135° (corresponding angles)
∠3 = ∠8 = 135° (corresponding angles)
∠3 = ∠5 = 135° (Alternate interior angles)
∠1 + ∠7 = 180° (co-exterior angles are supplementary)
135° + ∠7 = 180°
∠7 = 180°- 135° = 45°
∠6 = ∠7 = 45° (vertically opposite angles)
∠6 = ∠2 = 45° (corresponding angles)
∠4 = ∠7 = 45° (corresponding angles)
∴ ∠1 = 135°, ∠2 = 45°, ∠3 = 135°, ∠4 = 45°, ∠5 = 135°, ∠6 = 45°, ∠7 = 45°, ∠8 = 135°
Question 2.
In the given figure, \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\) and \(\overleftrightarrow{\mathbf{DE}}\) is a transversal. Find x.
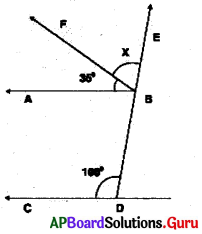
Answer:
Given \(\overleftrightarrow{\mathbf{AB}}\) || \(\overleftrightarrow{\mathbf{CD}}\) and \(\overleftrightarrow{\mathbf{DE}}\) is a transversal line.
∠ABE = ∠CDB (corresponding angles)
∠ABF + ∠FBE = ∠CDB (we know ∠ABE = ∠ABF + ∠FBE)
From the figure ∠ABF = 35°,
∠FBE = x° and ∠CDB =100°
35° + x = 100°
⇒ 35° + x – 35° = 100° – 35°
∴ x = 65°
![]()
Question 3.
In the given figure, m || n and p is transversal. Find x and y.
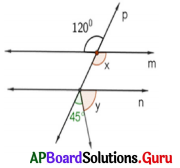
Answer:
Given m || n and p is transversal.
So, ∠x = 120° (vertically opposite angles)
45 + y = x (corresponding angles)
⇒ 45 + y = 120° (we know ∠x = 120°)
⇒ 45 + y – 45 = 120-45°
⇒ y = 75°
x = 120° and y = 75°
Question 4.
In the given figure, \(\overrightarrow{\mathbf{A B}}\|\overrightarrow{\mathbf{C D}}\| \overrightarrow{\mathbf{F E}}\). Find x, y and ∠AEC.
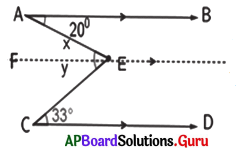
Answer:
Given \(\overrightarrow{\mathbf{A B}}\|\overrightarrow{\mathbf{C D}}\| \overrightarrow{\mathbf{F E}}\)
∠x = 20° (Alternate interior angles)
∠y = 33° (Alternate interior angles)
∠AEC = ∠AEF + ∠FEC
∠AEC = ∠x + ∠y
∠AEC = 20° + 33° = 53°
∴ x = 20°, y = 33° and ∠AEC = 53°
Question 5.
In the given figure, a transversal t intersects two lines p and q. Check whether p ∥q or not.
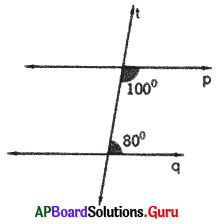
Answer:
If co-interior angles are supplementary, then the lines are parallel.
100° + 80° = 180° (co-interior angles supplementary)
So, p and q are parallel to each other.
Question 6.
In the given figure if l ∥m, then find x, y and z.
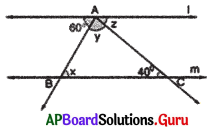
Answer:
Given l ∥m and AC is transversal.
z = 40° (Alternate interior angles)
l ∥m and AB is transversal. , and x + (y + z) = 180° (co-interior angles are supplementary)
x + y + z = 180°
(x + y) + 40° = 180° (co-interior angles are supplementary) (∵ z = 40°)
x + y + 40° = 180°
x + y + 40°-40° = 180° – 40°
∴ x + y = 140°
But x = y (given)
2x = 140°
∴ x = \(\frac{140^{\circ}}{2}\) = 70° = y
So, x = 70°, y = 70° and z = 40°
![]()
Question 7.
In the given figure p, q, r and s are parallel lines and t is a transversal. Find x, y and z.
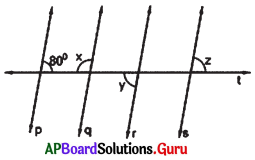
Answer:
p ∥ q
So, 80° + x = 180° (co-interior angles)
80° + x-80° = 180°-80°
x = 100°
q ∥ r
x + y = 180° (co-interior angles)
100° + y = 180° (we know x – 100°)
100° + y – 100° = 180°- 100°
y = 80°
r∥s
y = z (Alternate exterior angles)
y = z = 80° (we know y = 80°)
x = 100°, y = 80° and z = 80°
Question 8.
In the given figure \(\overrightarrow{\mathbf{A B}} \| \overrightarrow{\mathbf{C D}}\) and E is a point in between them. Find x + y + z. (Hint : Draw a parallel line to \(\overrightarrow{\mathbf{A B}}\) through E)
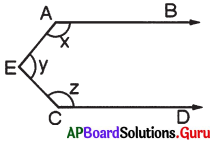
Answer:
Given \(\overrightarrow{\mathbf{A B}} \| \overrightarrow{\mathbf{C D}}\)
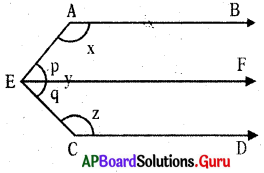
Draw \(\overrightarrow{\mathrm{EF}} \| \overrightarrow{\mathrm{AB}}\)
∠BAE = x,
∠AEF = p
∠FEC = q,
∠ECD = z
∠AEC = ∠AEF + ∠FEC
y = p + q
AB ∥ EF and AE is a transversal.
∠BAE + ∠AEF = 180° (co-interior angles are supplementary)
x + p = 180° ……………….(1)
CD ∥ EF and EC is a transversal.
∠FEC + ∠ECD = 180° (co-interior angles are supplementary’)
q + z = 180° …………….(2)
By adding (1) and (2)
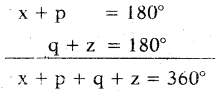
x + y. + z = 360° (we know y = p + q)
Question 9.
Identify the pair of parallel lines in the given figure and write them.
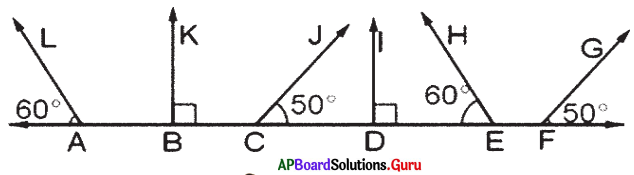
Answer:
∠A = ∠E = 60° So, AL ∥ EH
∠B = ∠D = 90° So, BK ∥ DL
∠C = ∠F = 50° So, CJ ∥ FG