AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties Ex 4

AP State Syllabus AP Board 7th Class Maths Solutions Chapter 5 Triangle and Its Properties Ex 4 Textbook Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 5th Lesson Triangle and Its Properties Exercise 4

Question 1.
In ΔABC, name all the interior and exterior angles of the triangle.

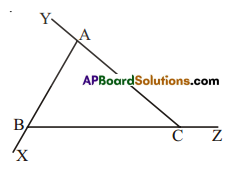
Solution:
Interior angles
∠ABC, ∠BAC, ∠CAB
Exterior angles
∠ACZ, ∠BAY and ∠CBX

Question 2.
For ΔABC, find the measure of ∠ACD.

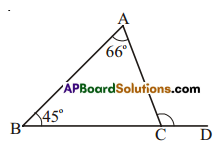
Solution:
In ΔABC,
∠ACD = ∠BAC + ∠ABC (exterior angle property)
=66° + 45° = 111°.

Question 3.
Find the measure of angles x and y.

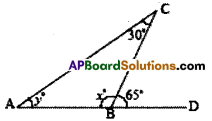
Solution:
In the figure,
x° + 65° = 180° (lInear pair of an1es)
∴ x°= 180°- 65°= 115°
Also y° + 30° = 65° (exterior angle property)
y° = 65° – 30° = 35°

Question 4.
In the following figures, fmd the values of x and y.


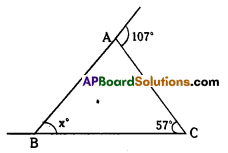
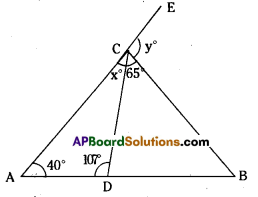
Solution:
In ΔABC,
107° = x° + 57° (exterIor angle property)
∴ x° = 107° – 57° =50°
In ΔADC,
∠CAD + ∠ADC + ∠ACD = 180° (angle – sum property)
40° + 107°+ x°= 180°
∴ x° = 180° – 147° = 33°
Also in ΔABC,
∠A +∠B +∠C = 180°
40° + ∠B + (33° + 65°) = 180°
∠B + 138° = 180°
B = 180° – 138° = 42°
Now y° = ∠A + ∠B for ΔABC (exterior angle property)
=40° + 42° = 82°

Question 5.
In the figure ∠BAD = 3 ∠DBA, find ∠CDB. ∠DBC and ∠ABC.

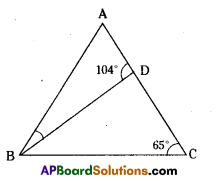
Solution:
In ΔBCD,
∠DBC + ∠BCD = ∠BDA (exterior angle property)
∠DBC + 65° -104°
∴ ∠DBC = 104° – 65° = 39°
Also ∠BDA + ∠BDC = 180° (linear pair of angles)
104° + ∠BDC = 180°
∠CDB or ∠BDC = 180° – 104° = 76°
Now in ΔABD,
∠BAD + ∠ADB + ∠DHA = 180°
3∠DBA + ∠DBA + 104° = 180° (given)
4∠DBA + 104° – 180°
∴ 4∠DBA = 180° – 104°= 76°
∴∠DBA = \(\frac{76^{\circ}}{4}\) = 19°
Now ∠ABC = ∠DBA + ∠DBC = 19° + 39° = 58°

Question 6.
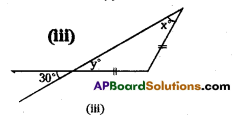
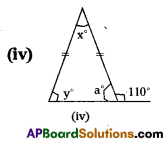
Find the values of x and y in the following figures.




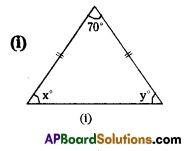
Solution:
i) In the figure the angles are
70°, x°, x° (angles in an Isosceles triangle)
Also 70° + x° + x° = 180° (angle – sum property)
2x° + 70°= 180°
2x° = 180° – 70° [∵ y° = x°]
2x° = 110°
x°= \(\frac{110^{\circ}}{2}\) = 55°

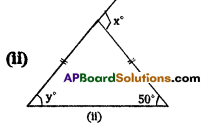
ii) From the figure,
the Interior opposite angles of x are 50°, 500 (angles in an isosceles triangle )
50° + 50° = x° (exterior angle is equal to sum of the Interior opposite angles)
∴ x = 100°

iii) From the figure,
y° = 30° (vertically opposite angles)
ALso y = x° – 30° (equal angles of an Isosceles triangles)
∴ x° = 30° and y = 30°

iv) From the figure,
a + 110° = 180° (linear pair of angles)
∴ a = 180° – 110°= 70
Also y° = a° = 70° (equal angles of an isosceles triangle)
x + y + a = 180 (sum of interior angles)
x + 70 + 70 = 180
x + 140 = 180
x = 180 – 40 = 40°, ∴ x = 40°

v) From the figure,
30° + y° – 180°
y° = 180° – 30° = 150°
Also x° + a° = y° (exterior angle property)
x° + 90° = 150°
x° = 150° – 90° = 60°

vi) From the figure,
b = 80° (vertically opposite angles)
Also x° = a° (equal angles of an isosceles triangle.)
° 80° + x° + a° = 180
80 + x° + x° = 180
2x° = 180° – 80° =100°
2x° = 100°
∴ x° = \(\frac{100}{2}\) = 50°
Now y = x° b° (exterior angle property)
50° + 80° = 130°

Question 7.
One of the exterior angles of a triangle is 125° and the interior opposite angles are in the
ratio 2 :3. Find the angles of the triangle.
Solution:
Ratio of the interior opposite angles = 2 : 3
Sum of the terms of the ratio = 2 + 3 = 5
Sum of the interior angles exterior angle = 125°
∴ First angle = \(\frac{2}{5}\) x 125° = 500
Second angle = \(\frac{3}{5}\) x 125° = 75°

Question 8.
The exterior ∠PRS of ∆PQR is 105°. If Q = 70°. find ∠P. Is ∠PRS > ∠P?
Solution:

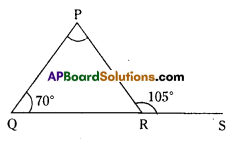
∠P+ ∠Q = ∠PRS (exterior angle is equal to sum of the interior opposite angles)
∠P + 70° = 105°
∠P = 105° – 70° = 35°
Now ∠PRS > ∠P.

Question 9.
If an exterior angle of a triangle is 130° and one of the interior opposite angle is 6. Find
the other interior opposite angle.
Solution:
Let the other interi6r opposite angle be = x°
Give interior opposite angle be = 60°
Now sum of the interior opposite angle = exterior angLe
x° + 60° = 130°
x° = 130° – 60° = 70°
∴ The other interior opposite angle = 70°

Question 10.
One of the exterior angle ofa triangle is 105° and the interior opposite angles are in the ratio 2 : 5. Find the angles of the triangle.
Solution:
Ratio of interior opposite angles = 2 : 5
Sum of the terms of the ratio = 2 + 5 = 7
Sum of the angles = 105°
∴ 1st angle = \(\frac { 2 }{ 7 }\) x 105° = 30°
2nd angIe = \(\frac { 5 }{ 7 }\) x 105° = 75°
3rd angle = 180° – (30° + 75°) [∵ angle – sum property]
= 180° – (105°) = 75°

Question 11.
In the figure find the values of x andy.
Solution:

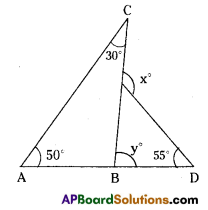
From the figure,
∠y = 50° + 30° = 80° (exterior angle property)
∠x = y° + 55° (exterior angle property)
= 80° + 55°
= 135°