AP Board 7th Class Maths Solutions Chapter 8 Exponents and Powers Ex 8.1

SCERT AP 7th Class Maths Solutions Pdf Chapter 8 Exponents and Powers Ex 8.1 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Exponents and Powers Ex 8.1

Questions 1.
Express the following into the exponential form:
(i) 14 × 14 × 14
Answer:
14 × 14 × 14 = 143

(ii) 25 × 25 × 25 × 25 × 25
Answer:
25 × 25 × 25 × 25 × 25 = 25

(iii) ab × ab × ab × ab
Answer:
ab × ab × ab × ab = (ab)⁴

(iv) 7 × p × p × q
Answer:
7 × p × p × q = 7 × p² × q

Question 2.
Express the following into expanded form:
(i) 27⁶
Answer:
27⁶ = 27 × 27 × 27 × 27 × 27 × 27

(ii) 101⁵
Answer:
1015 = 101 × 101 × 101 × 101 × 101

(iii) (2b)⁴
Answer:
2b⁴ = 2b × 2b × 2b × 2b

(iv) 3a⁸
Answer:
3a⁸ = 3 × a× a × a × a × a × a × a × a

Question 3.
Express the following In exponential form through prime factorisation: .
(i) 81
Answer:

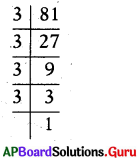
81 = 3 × 27
= 3 × 3 × 9
= 3 × 3 × 3 × 3
∴ 81 = 3⁴

(ii) 125
Answer:

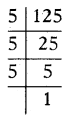
125 = 5 × 25
= 5 × 5 × 5
∴ 125 = 5³

(iii) 324
Answer:

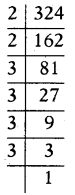
324 = 2 × 162
= 2 × 2 × 81
= 2 × 2 × 3 × 11
= 2 × 2 × 3 × 3 × 9
= 2 × 2 × 3 × 3 × 3 × 3
∴ 324 = 2² × 3⁴

(iv) 1080
Answer:

1080 = 2 × 540
= 2 × 2 × 270
= 2 × 2 × 2 × 135
= 2 × 2 × 2 × 3 × 45
= 2 × 2 × 2 × 3 × 3 × 15
= 2 × 2 × 2 × 3 × 3 × 3 × 5
∴ 1080 = 2³ × 3¹ × 5¹

Question 4.
Compute and identify the greater num-ber in the following pairs : 7
(i) 2⁵ or 5²
Answer:
2⁵ = 2 × 2 × 2 × 2 × 2 = 32
5² = 5 × 5 = 25
32 > 25
Therefore, 2⁵ > 5²

(ii) 7³ or 3⁷
Answer:
7³ = 7 × 7 × 7 = 343
3⁷ = 3 × 3 × 3 × 3 × 3 × 3 × 3 = 2187
2187 > 343
Therefore, 3⁷ > 7³

(iii) 2³ or 3²
Answer:
2³ = 2 × 2 × 2 = 8
3² = 3 × 3 = 9
9 > 8
Therefore, 3² > 2³

Question 5.
Expand 3³ × 4² and 4³ × 3². Are they equal? Justify.
Answer:
3³ × 4² = 3 × 3 × 3 × 4 × 4
= 27 × 16 = 432

4³ × 3² = 4 × 4 × 4 × 3 × 3
= 64 × 9 = 576

432 × 576 (They are not equal)
Therefore, 576 > 432
So, 4³ × 3² > 3³ × 4²

Question 6.
Express the following numbers in exponential form with the given base.
(i) 1000, base 10
Answer:

∴ 1000 = 10 × 10 × 10 = 10³

(ii) 512 base 2
Answer:

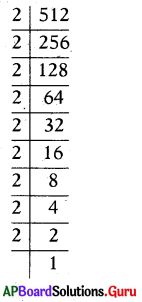
512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
∴ 512 = 2⁹

(iii) 243 base 3
Answer:

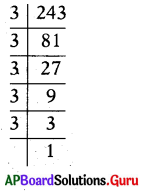
243 = 3 × 3 × 3 × 3 × 3
∴ 243 = 3⁵

Question 7.
If a = 2, b = 3 find the value of
(i) a^a + b^b
Answer:
Given a = 2, b = 3
a^a + b^b = 2² + 3³
= (2 × 2) + (3 × 3 × 3)
= 4 + 27 = 31
Therefore, if a = 2, b = 3 then a^a + b^b = 31

(ii) a^b + b^a
Answer:
Given a = 2, b = 3
a^b + b^a = 2³ + 3²
= (2 × 2 × 2) + (3 × 3).
= 8 + 9 = 17
Therefore, if a = 2, b = 3
then a^b + b^a = 17

(iii) (a + b)^b
Answer:
Given a = 2, b = 3
(a + b)^b = (2 + 3)³ = 5³
= 5 × 5 × 5 = 125
Therefore, if a = 2, b == 3
then (a + b)^b =125

Question 8.
Write the following in Exponential form:
(i) The speed of light in vacuum is about 30,00,00,000 m/sec.
Answer:
Given the speed of light = 30,00,00,000 m/sec
= 3 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10
∴ Speed of light = 3 × 10⁸ m/sec.

(ii) The population of India is about 121,00,00,000 as per 2011 census.
Answer:
Given population of India
= 121,00,00,000
= 121 × 10 × 10 × 10 × 10 × 10 × 10 × 10
= 11 × 11 × 10⁷
∴ Population of India = 11² × 10⁷ as per 2011 census.