AP Board 7th Class Maths Solutions Chapter 8 Exponents and Powers Ex 8.2

SCERT AP 7th Class Maths Solutions Pdf Chapter 8 Exponents and Powers Ex 8.2 Textbook Exercise Questions and Answers.

AP State Syllabus 7th Class Maths Solutions 8th Lesson Exponents and Powers Ex 8.2

Question 1.
Simplify the following by using Laws of Exponents.
(i) 3⁷ × 3⁸
Answer:
3⁷ × 3⁸
We know a^m × aⁿ = a^m+n
3⁷ × 3⁸ = 3⁷ + 8 = 3¹⁵
∴ 3⁷ × 3⁸ =3¹⁵

(ii) 9² × 9⁰ × 9³
Answer:
9² × 9⁰ × 9³
We know a^p × a^q × a^r = p + q + r
9² × 9⁰ × 9³ = 9^{2 + 0 + 3} = 9⁵
∴ 9² × 9⁰ × 9³ = 9⁵

(iii) (2⁸)³
Answer:
(2⁸)³
We know (a^m)ⁿ = a^mn
(2⁸)³ = 2^8×3 =2²⁴
∴ (2⁸)³ = 2²⁴

(iv) (a⁵)⁴
Answer:
(a⁵)⁴
We Know (a^m)ⁿ = a^mn
(a⁵)⁴ = a^5×4 = a²⁰
(a⁵)⁴ = a²⁰

(v) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{2}{5}\right)^{3} \times\left(\frac{2}{5}\right)^{8}\)
Answer:

(vi) 7⁵ ÷ 7⁸
Answer:
7⁵ ÷ 7⁸
We know a^m = \(\frac{1}{a^{n-m}}\) (n>m)
7⁵ ÷ 7⁸ = \(\frac{1}{7^{8-5}}=\frac{1}{7^{3}}\)
∴ 7⁵ ÷ 7⁸ = \(\frac{1}{7^{3}}\)

(vii) \(\frac{(-6)^{9}}{(-6)^{5}}\)
Answer:
\(\frac{(-6)^{9}}{(-6)^{5}}\)
We Know a^m ÷ aⁿ = a^m-n(m > n)
\(\frac{(-6)^{9}}{(-6)^{5}}\) = (-6)^9-5 = (-6)⁴
∴ \(\frac{(-6)^{9}}{(-6)^{5}}\) = (-6)⁴

(viii) (6⁴ × 6²) ÷ 6⁵
Answer:
(6⁴ × 6²) ÷ 6⁵
We know atm X a = a”
= (6⁴⁺²) ÷ 6⁵
= 6⁶ ÷ 6⁵
We know a^m ÷ aⁿ = a^m-n (m> n)
= 6^6-5 = 6¹ = 6
∴ (6⁴ × 6²) ÷ 6⁵ = 6

(ix) \(\frac{5^{3}}{2^{3}}\)
Answer:
\(\frac{5^{3}}{2^{3}}\)
We know \(\frac{a^{m}}{b^{m}}=\left(\frac{a}{b}\right)^{m}\)
∴ \(\frac{5^{3}}{2^{3}}=\left(\frac{5}{2}\right)^{3}\)

(x) (-3)³ × (-3)¹⁰ × (-3)⁷
Answer:
(-3)³ × (-3)¹⁰ × (-3)⁷
we know a^p . a^q. a^r = a^p+q+r
(-3)³ × (-3)⁰ × (-3)⁷ = (-3)³⁺¹⁰⁺⁷
∴ (- 3)³ × (- 3)¹⁰ × (- 3)⁷ = (- 3)²⁰

Question 2.
Simplify and express each of the following in Exponential form.
(i) \(\left(\frac{a^{5}}{a^{3}}\right)\) × a⁸
Answer:
\(\left(\frac{a^{5}}{a^{3}}\right)\) × a⁸
We Know \(\frac{a^{m}}{a^{n}}\) = a^m-n(m > n)
= (a^5-3) × a⁸
= a² × a⁸

We know a^m × aⁿ = a^m+n
= a²⁺⁸ = a¹⁰
∴ \(\left(\frac{a^{5}}{a^{3}}\right)\) × a⁸ = a¹⁰

(ii) 2⁰ + 3⁰ – 4⁰
Answer:
2⁰ + 3⁰ – 4⁰
We know a⁰ = 1

∴ 2⁰ + 3⁰ – 4⁰ = 1

(iii) (2³ × 2)²
Answer:
(2³ × 2)²
We know a^m.aⁿ = a^m+n
(2³ × 2)² = (2³⁺¹)² = (2⁴)²

We know (a^m)ⁿ = a^m.n
= 2^4×2 = 2⁸
∴(2³ × 2)² = 2⁸

(iv) [(5²)³ × 5⁴] ÷ 5⁷
Answer:
[(5²)³ × 5⁴] ÷ 5⁷

We know (a^m) = a^m.n
= [5^2×3 × 5⁴] ÷ 5⁷
= [5⁶ < 5⁴] ÷ 5⁷

We know a^m .aⁿ = a^m+n
= [5⁶⁺⁴] ÷ 5⁷
= 5¹⁰ ÷ 5⁷
We know a^m ÷ aⁿ = a^m-n (m > n)
= 5^10-7 = 5³
∴ [(5²)³ × 5⁴] ÷ 5⁷ = 5³

Question 3.
Simplify \(\left(\frac{x^{a}}{x^{b}}\right) \times\left(\frac{x^{b}}{x^{c}}\right) \times\left(\frac{x^{c}}{x^{a}}\right)\)
Answer:
\(\left(\frac{x^{a}}{x^{b}}\right) \times\left(\frac{x^{b}}{x^{c}}\right) \times\left(\frac{x^{c}}{x^{a}}\right)\)

Question 4.
Find the value of the following.
(i) (-1)¹⁰⁰⁰
Answer:
(-1)¹⁰⁰⁰
(-1)¹ = – 1
(-1)² = – 1 × – 1 = + 1
(-1)³ = – 1 × -1 × -1 = – 1
(-1)⁴ = -1 × -1 × – 1 × – 1 = + 1
(-1)⁵ = -1 × -1 × -1 × -1 × -1 = -1
(-1)¹⁰⁰ = -1 × -1 × -1 × ………… 100 times = + 1

So, (-1)^{odd number} = -1 and
(-1)^{even number} = + 1

Here 1000 is even number
So, (-1)¹⁰⁰⁰ = + 1

(ii) (1)²⁵⁰
Answer:
1²⁵⁰ = 1 × 1 × 1 ……… 250 times = 1
∴ 1²⁵⁰ = 1

(iii) (1)¹²¹
Answer:
1¹²¹ = -1 × -1 × -1 ……..(121 times)
Here 121 is an odd number
So, (1)¹²¹ = – 1

(iv) (10000)⁰
Answer:
(10000)⁰
we know a⁰ = 1
So, (10000)⁰ = 1

Question 5.
If 7⁵ × 7^3x = 7²⁰ then find the value of ’x’.
Answer:
Given, 7⁵ × 7^3x = 7²⁰
W know a^m X aⁿ = a^m+n
7^{5 + 3x} = 7²⁰
If the bases are equal, then the powers should also be equal.
⇒ 5 + 3x = 20
⇒ 5 + 3x – 5 = 20 – 5
⇒ 3x = 15
⇒ \(\frac{3 x}{3}=\frac{15}{3}\) = 5
∴ x = 5

Question 6.
If 10^y = 10000 then 5y =?
Answer:
Given, 10^y = 10000
10^y = 10 × 10 × 10 × 10
10^y = 10⁴
If the bases are equal, then the powers should also be equal.
⇒ y = 4
Multiply by 5 on bothsides,
5 × y = 5 × 4
∴ 5y = 20

Question 7.
If 5^x = 100 then find the following values.
(i) 5^x+y
Answer:
Given 5^x+y = 100
5^x = 10²
Multiply by 5²
5^x × 5² = 100 × 5²
5^x+2 = 100 × 25 (∵ a^m × aⁿ = a^m+n)
∴ 5^x+2 = 2500

(ii) 5^x-2
Answer:
Given 5^x = 100
5^x = 10²
Divide by 5² on both sides
5^x ÷ 5² = 100 ÷ 5²

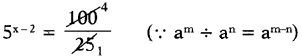
∴ 5^x-2 = 4

Question 8.
By what number should 3⁴ be multiplied so that the product is 243?
Answer:
Given number is 3⁴
If we multiply 3⁴ by ‘a’ the product is 243.
i.e. 3⁴ × a = 243
= 3 × 3 × 3 × 3 × 3
3⁴ × a = 35
Divide by 3⁴ on both sides

If we multiply 3⁴ by 3 we get 243.

Question 9.
Arushi computed (5²)⁴ as 5¹⁶ Has she done it correctly or not’? Justify your answer.
Answer:
Given, (5²)⁴
We know) (a^m)ⁿ = a^m.n
= 5^2×4 = 5⁸
∴ (5²)⁴ = 5⁸
But Arushi got 5¹⁶ So, (5²)⁴ ≠ 5¹⁶
Therefore Arushi did wrong.

Question 10.
Is 3⁵ × 4⁵ equal to 12²⁵? If not why? Justify your answer.
Answer:
Given, 3⁵ × 4⁵
We know a^m × b^m = (a × b)^m
So, 3⁵ × 4⁵ = 12 but not 12^5×5
= (3 × 4)⁵
= (12)⁵
3⁵ × 4⁵= 12⁵
But given 3⁵ × 4⁵ = 12²⁵.
So, this is wrong.
So, 3⁵ × 4⁵ ≠ 12²⁵