SCERT AP 7th Class Maths Solutions Pdf Chapter 8 Exponents and Powers Unit Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 8th Lesson Exponents and Powers Unit Exercise
Question 1.
Answer the following.
(i) The exponential form 149 should read as
Answer:
14 is raised to the power of 9.
(ii) When base is 12 and exponent is 17, it’s exponential form is _________
Answer:
1217.
(iii) The value of (14 × 21)0 is
Answer:
We know a0 = 1
So, (14 × 21)0 = 1
Question 2.
Express the following numbers as a product of powers of prime factors :
(i) 648
Answer:

Given 648 = 2 × 324
= 2 × 2 × 162
= 2 × 2 × 2 × 81
= 2 × 2 × 2 × 3 × 27
= 2 × 2 × 2 × 3 × 3 × 9
= 2 × 2 × 2 × 3 × 3 × 3 × 3
∴ 648 = 23 × 34
(ii) 1600
Answer:
Given 1600 = 2 × 800
= 2 × 2 × 400
= 2 × 2 × 2 × 200
= 2 × 2 × 2 × 2 × 100
= 2 × 2 × 2 × 2 × 2 × 2 × 25
= 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5

∴ 1600 = 26 × 52
(iii) 3600
Answer:

Given 3600 = 2 × 1800
= 2 × 2 × 900
= 2 × 2 × 2 × 450
= 2 × 2 × 2 × 2 × 225
= 2 × 2 × 2 × 2 × 3 × 75
= 2 × 2 × 2 × 2 × 3 × 3 × 25
= 2 × 2 × 2 × 2 × 3 × 3 × 5 × 5
∴ 3600 = 24 × 32 × 52
![]()
Question 3.
Simplify the following using laws of exponents.
(i) a4 × a10
Answer:
a4 × a10
We know am × an = am+n
= a4+10
∴ a4 × a10 = a14
(ii) 1818 ÷ 1814
Answer:
1818 ÷ 1814
We Know am ÷ an = am-n
= 1818-14
∴ 1818 ÷ 1814 = 184
(iii) (xm)0
Answer:
(xm)0
We Know (am)n = am.n
= xm×n = x0(∵ a0 = 1)
∴ (xm)0 = 1
(iv) (62 × 64) ÷ 63
Answer:
(62 X 64) ÷ 63
We Know am × an = am+n
= (62+4) ÷ 63
= 66 ÷ 63
We Know am ÷ an = am-n
= 66-3
∴ (62 × 64) ÷ 63 = 63
(v) \(\left(\frac{2}{3}\right)^{p}\)
Answer:
\(\left(\frac{2}{3}\right)^{p}\)
We Know \(\left(\frac{a}{b}\right)^{m}=\frac{a^{m}}{b^{m}}=\frac{2^{p}}{3^{p}}\)
∴ \(\left(\frac{2}{3}\right)^{\mathrm{p}}=\frac{2^{\mathrm{p}}}{3^{\mathrm{p}}}\)
Question 4.
Identify the greater number in each of the following andjustify your answer.
(i) 210 or 102
Answer:
210 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
210 = 1024
102 = 10 × 10
102 = 100
1024 > 100
So, 210 > 102
∴ 210 is greater.
(ii) 54 or 45
Answer:
54 = 5 × 5 × 5 × 5 = 625
45 =4 × 4 × 4 × 4 × 4 = 1024
1024 > 625
So, 45 > 54
∴ 45 is greater number.
Question 5.
If \(\left(\frac{4}{5}\right)^{2} \times\left(\frac{4}{5}\right)^{5}=\left(\frac{4}{5}\right)^{k}\), then find the value of ‘k’
Answer:
Given \(\left(\frac{4}{5}\right)^{2} \times\left(\frac{4}{5}\right)^{5}=\left(\frac{4}{5}\right)^{k}\)
We Know am × an = am+n
⇒ \(\left(\frac{4}{5}\right)^{2+5}=\left(\frac{4}{5}\right)^{\mathrm{k}}\)
⇒ \(\left(\frac{4}{5}\right)^{7}=\left(\frac{4}{5}\right)^{\mathrm{k}}\)
If the bases are equal powers should be equal
⇒ 7 = k
∴ k = 7
![]()
Question 6.
If 52p+1 ÷ 52 = 125, then find the value of ‘p’.
Answer:
Given 52p+1 ÷ 52 = 125
We Know am ÷ an = am-n
⇒ 52p+1-2 = 5 × 5 × 5
⇒ 52p-1 = 53
If the bases are equal, powers should be equal.
⇒ 2p – 1 =3
⇒ 2p = 3 + 1
⇒ 2p = 4
⇒ \(\frac{2 \mathrm{p}}{2}=\frac{4}{2}\)
∴ p = 2
Question 7.
Prove that \(\left(\frac{x^{b}}{x^{c}}\right)^{a} \times\left(\frac{x^{c}}{x^{a}}\right)^{b} \times\left(\frac{x^{a}}{x^{b}}\right)^{c}\) = 1
Answer:
Given \(\left(\frac{x^{b}}{x^{c}}\right)^{a} \times\left(\frac{x^{c}}{x^{a}}\right)^{b} \times\left(\frac{x^{a}}{x^{b}}\right)^{c}\) = 1
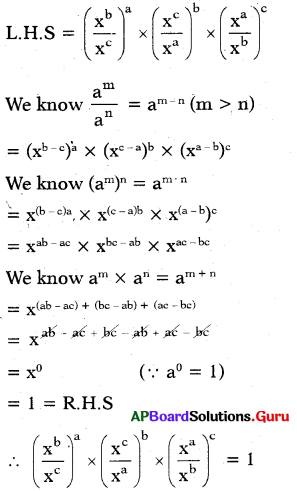
Question 8.
Express the following numbers in the expanded form.
(i) 20068
Answer:
20068 = (2 × 10,000) + (0 × 1000) + (0 × 100) + (6 × 10) + (8 × 1)
∴ 20068 = (2 × 104) + (6 × 101) + (8 × 1)
(ii) 120718
Answer:
120718 = (1 × 1,00,000) + (2 × 10,000) + (0 × 1000) + (7 × 100) + (1 × 10) + (8 × 1)
∴ 120718 = (1 × 105) + (2 × 104) + (7 × 102) + (1 × 101) + (8 × 1)
Question 9.
Express the number appearing in the following statements in standard form :
(i) The Moon is 384467000 meters away from the Earth approximately.
Answer:
Distance of Moon from the Earth = 384467000 metres
= 3.84467000 × 100000000
Decimal is shifted eight places to the left.
= 3.84 4 67 × 108 m
Distance of Moon from the earth = 3.84 4 67 × 108 m
(ii) Mass of the Sun is 1 ,989,000,000,000,000,000,00000,000000 kg.
Answer:
Mass of Sun = 1 ,989,000,000,000,000,000,00000,000000 kg
= 1.989 × 1 ,000,000,000,000,000,00000,000000
= 1.989 × 1030 kg
∴ Mass of Sun = 1.989 × 1030 kg.
Question 10.
Lasya solved some problems of exponents and powers in the following way. Do you agree with the solution ? If not why? Justify your answer.
Answer:
(i) x3 × x2 = x6
Answer:
No. I won’t agree with this solution.
Given, x3 × x2
We know am × an = am+n
= a3+2
= x5 which is ≠ x6
so, x3 × x2 ≠ x6
We have to add to powers. But, Lasya multiplied the powers. That’s why Lasya’s solution is wrong.
(ii) (63)10 = 613
Answer:
No, (63)10 is not equal to 6.
We know (am)n = amn
= 63×10
= 630 which is ≠ 613
so, (63)10 ≠ 613
We have to multiply. the powers. But, Lasya added the powers. That’s why Lasya’s solution is wrong.
(iii) \(\frac{4 x^{6}}{2 x^{2}}\) = 2x3
Answer:
No, I won’t agree with this solution.
\(\frac{4 x^{6}}{2 x^{2}}=\frac{2^{2}}{2^{1}} \times \frac{x^{6}}{x^{2}}\)
We know am ÷ an = am-n
= 22-1 × x6-2
= 21.x4
= 2x4 which is ≠ 2x3
so, \(\frac{4 x^{6}}{2 x^{2}}\) ≠ 2x3
We have to subtract the powers. But, Lasya divided the powers. That’s why Lasya’s solution is wrong.
(iv) \(\frac{3^{5}}{9^{5}}=\frac{1}{3}\)
Answer:
No. I won’t agree with this solution.
\(\frac{3^{5}}{9^{5}}=\frac{3^{5}}{\left(3^{2}\right)^{5}}\)
We Know (am)n = amn

We have to subtract the powers. But, Lasya divided the powers. That’s why Lasya’s solution is wrong.
![]()
Question 11.
Is – 22 is equal to 4? Justify your answer.
Answer:
– 22 = – (2 × 2) = – 4 ≠ 4
∴ – 22 = – 4
Question 12.
Beulah computed 25 × 210 = 250. Has she done it correctly? Give the reason.
Answer:
Given 25 × 210
We know am × an = am+n
= 25+10 = 215 ≠ 250
∴ 25 × 210 ≠ 250
Beulah did wrong.
Here we have to add the powers.
But, he multiplied the powers.
Question 13.
Rafi computed \(\frac{3^{9}}{3^{3}}\) as 33. Has he done
Answer:
Given \(\frac{3^{9}}{3^{3}}\)
We know \(\frac{a^{m}}{a^{n}}\) = am-n
= 39-3 = 36 ≠ 33
So, \(\frac{3^{9}}{3^{3}}\) ≠ 33
Rafi computed wrong.
Here we have to subtract the powers. But, he divided the powers.
Question 14.
Is (a2)3 equal to a8? Give the reason.
Answer:
Given (a2)3 equal to a8
We Know (am)n = amn
= (a2)3 = a2×3 = a6 ≠ a8
∴ (a2)3 = a6
We have to do 2 × 3 = 6, But not
23 = 2 × 2 × 2 = 8