SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.4 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.4
Question 1.
Find the value of the expression
2x2 – 4x + 5 when
(i) x = 1
(ii) x = – 2
(iii) x = 0.
Answer:
Given expression is 2x2 – 4x + 5
(i) When x = 1, then
= 2(1)2 – 4(1) + 5
= 2 × 1 – 4 + 5
= 2 – 4 + 5 = 3
When x = 1, then 2x2 – 4x + 5 = 3
![]()
(ii) When x = – 2, then
= 2(- 2)2 – 4(- 2) + 5
= 2(4) + 8 + 5
= 8 + 8 + 5 = 21
When x = – 2, then 2x2 – 4x + 5 = 21
(iii) When x = 0, then
= 2(0)2 – 4(0) + 5
= 2(0) – 0 + 5
= 0 – 0 + 5 = 5
When x = 0, then 2x2 – 4x + 5 = 5
Question 2.
Find the value of Expressions when m = 2, n = – 1.
(i) 2m + 2n
Answer:
Given expression is 2m + 2n
If m = 2, n = – 1, then
2m + 2n = 2(2) + 2(- 1) = 4 – 2 = 2
∴ If m = 2, n = – 1, then 2m + 2n = 2
(ii) 3m – n
Answer:
Given expression is 3m – n
If m = 2, n = – 1, then
3m – n = 3(2) -(-1) = 6 + 1 = 7
∴ If m = 2, n = – 1, then 3m – n = 7
(iii) mn – 2.
Answer:
Given expression is mn – 2
If m = 2, n = – 1, then
mn – 2 = 2 × (-1)-2
= – 2 – 2 = – 4
∴ If m = 2, n = – 1, then mn – 2 = – 4
![]()
Question 3.
Simplify and find the value of the expression 5x2 – 4 – 3x2 + 6x + 8 + 5x – 13 when x = – 2.
Answer:
Given expression is
5x2 – 4 – 3x2 + 6x + 8 + 5x – 13
= (5x2 – 3x2) + (6x + 5x) + (-4 + 8 – 13)
= (5 – 3)x2 + (6 + 5)x + (- 9)
= 2x2 + 11x – 9
If x = – 2, then 2x2 + 11x – 9
= 2(- 2)2 + 11 (- 2) – 9
= 2(4) – 22 – 9
= 8 – 22 – 9
∴ If x = – 2, then 2x2 + 11x – 9 = – 23
Question 4.
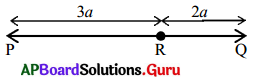
Find the length of the line segment PQ when a = 3 cm.
Answer:
From the figure,
Given PR = 3a and RQ = 2a
PQ = PR + RQ
= 3a + 2a
= (3 + 2)a
PQ = 5a
If a = 3 cm, then PQ = 5(3)
∴ PQ = 15 cm
Question 5.
The area of a square field of side ‘s’ meters is s2 sq. m. Find the area of square field, when
(i) s = 5m
(ii) s =12m
(iii) s = 6.5m

Answer:
From the figure,
Area of square = s2 sq.m.
(i) If s = 5m, then
s2 = (5)2 = 5 × 5 = 25 sq.m
(ii) If s = 12 m, then
s2 = (12)2 = 12 × 12 = 144 sq.m
(iii) If s = 6.5m, then
s2 = (6.5)2 = 6.5 × 6.5 = 42.25 sq.m
![]()
Question 6.
The area of triangle is given by \(\frac{1}{2}\) ∙ b ∙ h and if b = 12 cm, h = 8 cm, then find the area of triangle.
Answer:
Given area of the triangle = \(\frac{1}{2}\) ∙ b ∙ h
If b = 12 cm, h = 8 cm
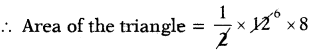
= 6 × 8 = 48 sq.cm.
Question 7.
Simple interest is given by I = \(\frac{\text { PTR }}{100}\), If P = ₹ 900, T = 2 years and R = 5%, then find the simple interest.
Answer:
Given simple interest I = \(\frac{\text { PTR }}{100}\)
If P = ₹ 900, T= 2 and R = 5% then
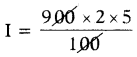
= 9 × 2 × 5 = 90
Question 8.
Find the errors and correct them in the following:
The value of following when a = – 3.
(i) 3 – a = 3 – 3 = 0
Answer:
3 – a = 3 – (- 3) (when a = – 3)
= 3 + 3 = 6
(Error is – (- 3) = – 3)
(ii) a2 + 3a = (- 3)2 + 3(- 3) = 9 + 0 = 9
Answer:
a2 + 3a = (- 3)2 + 3(- 3) (when a = – 3)
= (- 3 × – 3) – 9
(Error is 3(- 3) = 0)
= 9 – 9 = 0
![]()
(iii) a2 – a – 6 = (- 3)2 – (- 3) – 6 = 9 – 3 – 6 = 0
Answer:
a2 – a – 6
= (- 3)2 – (- 3) – 6 (when a = – 3)
= (- 3 × – 3) + 3 – 6
(Error is – (- 3) = – 3)
= 9 + 3 – 6
= 12 – 6 = 6
(iv) a2 + 4a + 4 = (- 3)2 + 4(-3) + 4 = 9 + 1 + 4 = 14
Answer:
a2 + 4a + 4
= (- 3)2 + 4(- 3) + 4 (when a = – 3)
= (- 3 × – 3)- 12 + 4
(Error is 4 (- 3) = 1)
= 9 – 12 + 4 = 13 – 12 = 1
(v) a3 – a2 – 3 = (- 3)3 – (-3)2 – 3 = – 9 + 6 – 3 = – 6
Answer:
a3 – a2 – 3
= (- 3)3 – (- 3)2 – 3 (when a = – 3)
= (- 3 × – 3 × – 3) – (- 3 × – 3) – 3
= – 27 – (9) – 3
(Error is (- 3)3 = – 9 and (- 3)2 = 6)
= – 27 – 9 – 3 = – 39