SCERT AP 7th Class Maths Solutions Pdf Chapter 9 Algebraic Expressions Ex 9.3 Textbook Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 9th Lesson Algebraic Expressions Ex 9.3
Question 1.
Write standard form and additive inverse of the following expressions.
(i) – 6a
Answer:
Additive inverse of – 6a = – (- 6a) = 6a
![]()
(ii) 2 + 7c2
Answer:
Standard form of 2 + 7c2 = 7c2 + 2
Additive inverse of 7c2 + 2
= – (7c2 + 2)
= – 7c2 – 2
(iii) 6x2 + 4x – 5
Answer:
Given expression is in standard form.
Additive inverse of 6x2 + 4x – 5
= – (6x2 + 4x – 5)
= – 6x2 – 4x + 5
(iv) 3c + 7a – 9b
Answer:
Standard form of 3c + 7a – 9b = 7a – 9b + 3c
Additive inverse of 7a – 9b + 3c
= – (7a – 9b + 3c)
= – 7a + 9b – 3c
Question 2.
Write the following expressions in standard form:
(i) 6x + x2 – 5
Answer:
Standard form of 6x + x2 – 5
= x2 + 6x – 5
(ii) 3 – 4a2 – 5a
Answer:
Standard form of 3 – 4a2 – 5a
= – 4a2 – 5a + 3
(iii) – m + 6 + 3m2
Answer:
Standard form of – m + 6 + 3m2
= 3m2 – m + 6
![]()
(iv) c3 + 1 + c + 2c2
Answer:
Standard form of
c3 + 1 + c + 2c2 = c3 + 2c2 + c + 1
(v) 9 – p2
Answer:
Standard form of 9 – p2 = – p2 + 9
Question 3.
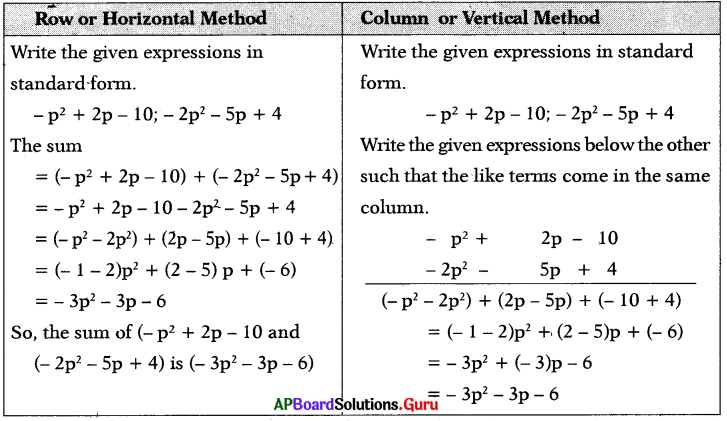
Add the following algebraic expressions using both horizontal and vertical methods. Did you get the same answer with both the methods? Verify.
(i) 2x2 – 6x +3; 4x2 + 9x + 5
Answer:

(ii) a2 + 6ab + 8; – 3a2 – ab – 2
Answer:

![]()
(iii) – p2 + 2p – 10; 4 – 5p – 2p2
Answer:
Question 4.
Subtract the second expression from the first expression:
(i) 2x + y , x – y
Answer:
Let A = 2x + y and B = x – y
A – B = A + (- B) Additive inverse of B is
-B = – (x – y) = – x + y
∴ A – B = A + (- B)
= 2x + y + (- x + y)
= 2x + y – x + y
= 2x – x + y + y
= (2 – 1)x + (1 + 1)y
∴ A – B = x + 2y
![]()
(ii) a + 2b + c, – a – b – 3c
Answer:
Let A = a + 2b + c and B = – a – b – 3c
A – B = A + (- B)
Additive inverse of B is
– B = – (- a – b – 3c)
= a + b + 3c
∴ A – B = A + (- B)
= a + 2b + c + (a + b + 3c)
= a + 2b + c + a + b + 3c
= (a + a) + (2b + lb) + (c + 3c)
∴ A – B = 2a + 3b + 4c
(iii) 2l2 – 3lm + 5m2, 3l2 – 4lm + 6m2
Answer:
Let A = 2l2 – 3lm + 5m2 and
B = 3l2 – 4lm + 6m2
A – B = A + (- B)
Additive inverse of B is
– B = – (3t2 – 4lm + 6m2)
= – 3l2 + 4lm – 6m2
∴ A – B = A + (- B)
= (2l2 – 3lm + 5m2) + (- 3l2 + 4lm – 6m2)
= 2l2 – 3lm + 5m2 – 3l2 + 4lm – 6m2
= 2l2 – 3l2 – 3lm + 4lm + 5m2 – 6m2
= (2 – 3)l2 + (- 3 + 4)lm + (5 – 6)m2
= (- 1) l2 + 1 lm + (- 1)m2
∴ A – B = – l2 + lm – m2
(iv) 7 – x – 3x2, 2x2 – 5x – 3
Answer:
Let A = 7 – x – 3x2 and B = 2x2 – 5x – 3
Write the given expressions in standard form.
∴ A = – 3x2 – x + 7 and B = 2x2 – 5x – 3
A – B = A + (- B)
Additive inverse of B is
– B = – (2x2 – 5x – 3)
= – 2x2 + 5x + 3
∴ A – B = A + (- B)
= (- 3x2 – x + 7) + (- 2x2 + 5x + 3)
= – 3x2 – x + 7 – 2x2 + 5x + 3
= (- 3x2 – 2x2) + (- x + 5x) + (7 + 3)
= (- 3 – 2)x2 + (- 1 + 5)x + 10
∴ A – B = – 5x2 + 4x + 10
![]()
(v) 6m3 + 4m2 + 7m – 3, 2m3 + 4
Answer:
Let A = 6m3 + 4m2 + 7m – 3 and
B = 2 m2 + 4
A – B = A + (- B)
Additive inverse of B is
– B = – (2m3 + 4)
= – 2m3 – 4
∴ A – B = A + (- B)
= (6m3 + 4m2 + 7m – 3) + (- 2m3 – 4)
= 6m3 + 4m2 + 7m – 3 – 2m3 – 4
= (6m3 – 2m3) + 4m2 + 7m + (- 3 – 4)
= (6 – 2)m3 + 4m2 + 7m + (- 7)
∴ A – B = 4m3 + 4m2 + 7m – 7
Question 5.
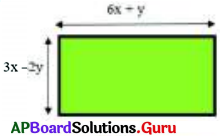
Find the perimeter of the beside rect¬angle whose length is 6x + y and breadth is 3x – 2y.
Answer:
Given length of rectangle l = 6x + y
breadth b = 3x – 2y
Perimeter of Rectangle = 2 (l + b)
= 2[(6x + y) + (3x – 2y)]
= 2[6x + y + 3x – 2y]
= 2[(6 + 3)x + (1 – 2)y]
= 2[9x + (- 1) y]
= 2[9x – 1y]
= 2 × (9x) – 2 × (1y)
∴ Perimeter of rectangle = (18x – 2y) units.
![]()
Question 6.
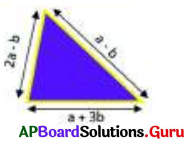
Find the perimeter of triangle whose sides are a + 3b, a – b and 2a – b.
Answer:
Let the sides of triangle are
x = a + 3b, y = a – b and z = 2a – b
Perimeter of triangle = x + y + z
= (a + 3b) + (a – b) + (2a – b)
= a + 3b + a – b + 2a – b
= (a + a + 2a) + (3b – b – b)
= (1 + 1 + 2)a + (3 – 1 – 1)b
Perimeter of triangle.
= (4a + b) units.
Question 7.
Subtract the sum of x2 – 5xy + 2y2 and y2 – 2xy – 3x2 from the sum of 6x2 – 8xy – y2 and 2xy – 2y2 – x2.
Answer:
Given expressions are
x2 – 5xy + 2y2 and y2 – 2xy – 3x2 and 6x2 – 8xy – y2 and 2xy – 2y2 – x2
Write the given expressions in the standard form
x2 – 5xy + 2y2 and – 3x2 – 2xy + y2 and 6x2 – 8xy – y2 and – x2 + 2xy – 2y2
Let the Sum
A = (x2 – 5xy + 2y2) + (- 3x2 – 2xy + y2)
= x2 – 5xy + 2y2 – 3x2 – 2xy + y2
= x2 – 3x2 – 5xy – 2xy + 2y2 + y2
= (1 – 3)x2 + (- 5 – 2)xy + (2 + 1)y2
A = – 2x2 – 7xy + 3y2
Let the Sum
B = (6x2 – 8xy – y2) + (- x2 + 2xy – 2y2)
= 6x2 – 8xy – y2 – x2 + 2xy – 2y2
= (6 – 1 )x2 + (- 8 + 2)xy + (- 1 – 2)y2
B = 5x2 – 6xy – 3y2
B – A = B + (- A)
Additive inverse of A is
– A = – (A)
= – (- 2x2 – 7xy + 3y2)
∴ – A = 2x2 + 7xy – 3y2
B – A = B + (- A)
= (5x2 – 6xy – 3y2) + (2x2 + 7xy – 3y2)
= (5 + 2)x2 + (- 6 + 7)xy + (- 3 – 3)y2
∴ B – A = 7x2 + xy – 6y2
![]()
Question 8.
What should be added to 1 + 2p – 3P2 to get p2 – p – 1 ?
Answer:
Given expressions are
1 + 2p – 3p2 and p2 – p – 1
Write the given expressions in the standard form.
– 3p2 + 2p + 1 and p2 – p – 1
Let A should be added to B to get C.
i.e. A + B = C
∴ A = C – B
Let B = – 3p2 + 2p + 1 and
C = p2 – p – 1
A = C + (- B )
Additive inverse B is
– B = – (- 3p2 + 2p + 1) .
– B = 3p2 – 2p – 1 .
A = (p2 – p – 1) + (3p2 – 2p – 1)
= p2 – p – 1 + 3p2 – 2p – 1
= (1 + 3)p2 + (- 1 – 2)p + (- 1 – 1)
∴ A = 4p2 – 3p – 2
∴ 4p2 – 3p – 2 is added to 1 + 2p – 3p2 to get p2 – p – 1.
Question 9.
What should be taken away from 3a2 – 4b2 + 5ab + 20 to get – a2 – b2 + 6ab + 3 ?
Answer:
Given expressions are
3a2 – 4b2 + 5ab + 20 and – a2 – b2 + 6ab +3
Let A be taken away from B to get C. that is A = B – C = B + (- C)
Let B = 3a2 – 4b2 + 5ab + 20 and C = – a2 – b2 + 6ab + 3 Additive inverse of C is
(- C) = – (- a2 – b2 + 6ab + 3)
= a2 + b2 – 6ab – 3
A = B + (- C)
= (3a2 – 4b2 + 5ab + 20) + (a2 + b2 – 6ab – 3)
= 3a2 – 4b2 + 5ab + 20 + a2 + b2 – 6ab – 3
= 3a2 + a2 – 4b2 + b2 + 5ab – 6ab + 20 – 3
= (3 + 1)a2 + (- 4 + 1)b2 + (5 – 6) ab + (20 – 3)
A = 4a2 – 3b2 – 1 ab + 17
So, 4a2 – 3b2 – 1 ab + 17 is taken away from 3a2 – 4b2 + 5ab + 20 to get – a2 – b2 + 6ab + 3.
![]()
Question 10.
If A = 4x2 + y2 – 6xy;
B = 3y2 + 12x2 + 8xy;
C = 6x2 + 8y2 + 6xy then,
find(i) A + B + C (ii) (A – B) – C
Answer:
Given A = 4x2 + y2 – 6xy
B = 3y2 + 12x2 + 8xy
C = 6x2 + 8y2 + 6xy
Write the given expressions in standard form.
A = 4x2 – 6xy + y2
B = 12x2 + 8xy + 3y2
C = 6x2 + 6xy + 8y2
(i) A + B + C = (4x2 – 6xy + y2) + (12x2 + 8xy + 3y2) + (6x2 + 6xy + 8y2)
= 4x2 – 6xy + y2 + 12x2 + 8xy + 3y2 + 6x2 + 6xy + 8y2
= (4x2 + 12x2 + 6x2) + (- 6xy + 8xy + 6xy) + (y2 + 3y2 + 8y2)
= (4 + 12 + 6) x2 + (- 6 + 8 + 6) xy + (1 + 3 + 8)y2
∴ A + B + C = 22x2 + 8xy + 12y2
(ii) (A – B) – C
A + (- B) + (- C)
Additive inverse of B is
– B = – (12x2 + 8xy + 3y2)
∴ – B = – 12x2 – 8xy – 3y2
Additive inverse of C is
– C = -(6x2 + 6xy + 8y2)
∴ – C = – 6x2 – 6xy – 8y2
A + (- B) + (- C)
= (4x2 – 6xy + y2) + (- 12x2 – 8xy – 3y2) + (- 6x2 – 6xy – 8y2)
= 4x2 – 6xy + y2 – 12x2 – 8xy – 3y2 – 6x2 – 6xy – 8y2
= (4x2 – 12x2 – 6x2) + (- 6xy – 8xy – 6xy) + (y2 – 3y2 – 8y2)
= (4 – 12 – 6)x2 + (- 6 – 8 – 6)xy + (1 – 3 – 8)y2
∴ (A – B) – C = – 14x2 – 20xy – 10y2