AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles Ex 12.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles Exercise 12.4
![]()
Question 1.
In the figure, ‘O’ is the centre of the circle. ∠AOB = 100°, find ∠ADB.
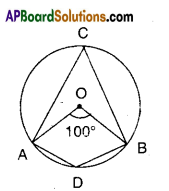
Solution:
’O’ is the centre
∠AOB = 100°
Thus ∠ACB = \(\frac{1}{2}\) ∠AOB
[∵ angle made by an arc at the centre is twice the angle made by it on the remaining part]]
= \(\frac{1}{2}\) x 100° = 50°
∠ACB and ∠ADB are supplementary
[ ∵ Opp. angles of a cyclic quadrilateral]
∴ ∠ADB = 180°-50° = 130°
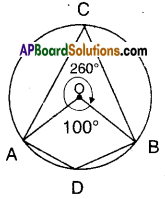
[OR]
∠ADB is the angle made by the major arc \(\widehat{\mathrm{ACB}}\) at D.
∴ ∠ADB = \(\frac{1}{2}\)∠AOB [where ∠AOB is the angle; made by \(\widehat{\mathrm{ACB}}\) at the centre]
= \(\frac{1}{2}\) [360° – 100°] [from the figure]
= \(\frac{1}{2}\) x 260° = 130°
![]()
Question 2.
In the figure, ∠BAD = 40° then find ∠BCD.
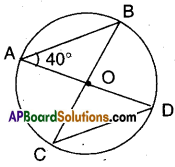
Solution:
‘O’ is the centre of the circle.
∴ In ΔOAB; OA = OB (radii)
∴ ∠OAB = ∠OBA = 40°
(∵ angles opp. to equal sides)
Now ∠AOB = 180° – (40° + 40°)
(∵ angle sum property of ΔOAB)
= 180°-80° = 100°
But ∠AOB = ∠COD = 100°
Also ∠OCD = ∠ODC [OC = OD]
= 40° as in ΔOAB
∴ ∠BCD = 40°
(OR)
In ΔOAB and ΔOCD
OA = OD (radii)
OB = OC (radii)
∠AOB = ∠COD (vertically opp. angles)
∴ ΔOAB ≅ ΔOCD
∴ ∠BCD = ∠OBA = 40°
[ ∵ OB = OA ⇒ ∠DAB = ∠DBA]
![]()
Question 3.
In the figure, ‘O’ is the centre of the circle and ∠POR = 120°. Find ∠PQR and ∠PSR.
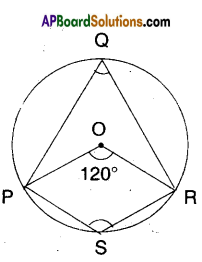
Solution:
‘O’ is the centre; ∠POR = 120°
∠PQR = \(\frac{1}{2}\)∠POR [∵ angle made by an arc at the centre is, twice the angle made by it on the remaining part]
∠PSR = \(\frac{1}{2}\) [Angle made by \(\widehat{\mathrm{PQR}}\) at the centre]
∠PSR = \(\frac{1}{2}\) [360° – 120°] from the fig.
= \(\frac{1}{2}\) x 240 = 120°
Question 4.
If a parallelogram is cyclic, then it is a rectangle. Justify.
Solution:
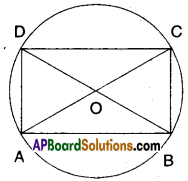
Let □ABCD be a parallelogram such
that A, B, C and D lie on the circle.
∴∠A + ∠C = 180° and ∠B + ∠D = 180°
[Opp. angles of a cyclic quadri lateral are supplementary]
But ∠A = ∠C and ∠B = ∠D
[∵ Opp. angles of a ||gm are equal]
∴∠A = ∠C =∠B =∠D = \(\frac{180}{2}\) = 90°
Hence □ABCD is a rectangle
![]()
Question 5.
In the figure, ‘O’ is the centr of the circle. 0M = 3 cm and AB = 8 cm. Find the radius of the circle.

Solution:
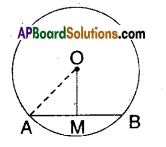
‘O’ is the centre of the circle.
OM bisects AB.
∴ AM = \(\frac{\mathrm{AB}}{2}=\frac{8}{2}\) = 4 cm
OA2 = OM2 + AM2 [ ∵ Pythagoras theorem]
OA \(\begin{array}{l}
=\sqrt{3^{2}+4^{2}} \\
=\sqrt{9+16}=\sqrt{25}
\end{array}\)
= 5cm
Question 6.
In the figure, ‘O’ is the centre of the circle and OM, ON are the perpen-diculars from the centre to the chords PQ and RS. If OM = ON and PQ = 6 cm. Find RS.
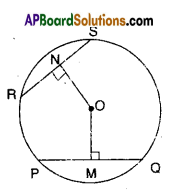
Solution:
‘O’ is the centre of the circle.
OM = ON and 0M ⊥ PQ; ON ⊥ RS
Thus the chords FQ and RS are equal.
[ ∵ chords which are equidistant from the centre are equal in length]
∴ RS = PQ = 6cm
![]()
Question 7.
A is the centre of the circle and ABCD is a square. If BD = 4 cm then find the
radius of the circle.
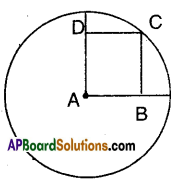
Solution:
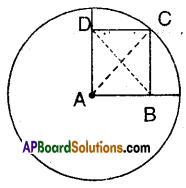
A is the centre of the circle and ABCD is a square, then AC and BD are its diagonals. Also AC = BD = 4 cm But AC is the radius of the circle.
∴ Radius = 4 cm.
Question 8.
Draw a circle with any radius and then draw two chords equidistant
from the centre.
Solution:
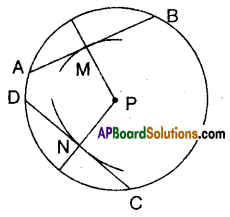
- Draw a circle with centre P.
- Draw any two radii.
- Mark off two points M and N oh these radii. Such that PM = PN.
- Draw perpendicular through M and N to these radii.
![]()
Question 9.
In the given figure, ‘O’ is the centre of the circle and AB, CD are equal chords. If ∠AOB = 70°. Find the angles of ΔOCD.
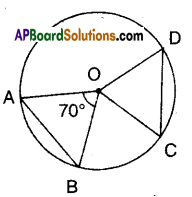
Solution:
‘O’ is the centre of the circle.
AB, CD are equal chords
⇒ They subtend equal angles at the centre.
∴ ∠AOB =∠COD = 70°
Now in ΔOCD
∠OCD = ∠ODC [∵ OC = OD; radii angles opp. to equal sides]
∴ ∠OCD + ∠ODC + 70° = 180°
= ∠OCD +∠ODC = 180° – 70° = 110°
∴ ∠OCD + ∠ODC = 110° = 55°