AP State Syllabus AP Board 9th Class Maths Solutions Chapter 7 Triangles Ex 7.1 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 7th Lesson Triangles Exercise 7.1
![]()
Question 1.
In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that ΔABC ≅ ΔABD What can you say about BC and BD ?
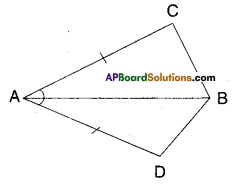
Solution:
Given that AC = AD
∠BAC = ∠BAD (∵ AB bisects∠A)
Now in ΔABC and ΔABD
AC = AD (∵ given)
∠BAC = ∠BAD (Y given)
AB = AB (common side)
∴ ΔABC ≅ ΔABD
(∵ SAS congruence rule)
![]()
Question 2.
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA, prove that i) ΔABD ≅ΔBAC ii) BD = AC
iii) ∠ABD = ∠BAC.
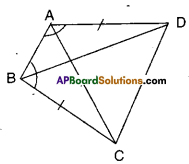
Solution :
i) Given that AD = BC and
∠DAB = ∠CBA
Now in ΔABD and ΔBAC
AB = AB (∵ Common side)
AD = BC (∵ given)
∠DAB = ∠CBA (∵ given)
∴ ΔABD ≅ ΔBAC
(∵ SAS congruence)
ii) From (i) AC = BD (∵ CPCT)
iii) ∠ABD = ∠BAC [ ∵ CPCT from (i)]
Question 3.
AD and BC are equal and perpendi-culars to a line segment AB. Show that CD bisects AB.
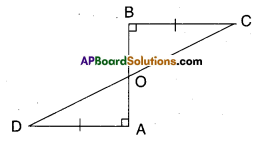
Solution:
Given that AD = BC; AD ⊥ AB; BC ⊥ AB
In ΔBOC and ΔAOD
∠BOC = ∠AOD (∵ vertically opposite angles)
∴ ΔOBC = ΔOAD (∵ right angle)
BC = AD
ΔOBC ≅ ΔOAD (∵ AAS congruence)
∴ OB = OA (∵ CPCT)
∴ ‘O’ bisects AB
Also OD = OC
∴ ‘O’ bisects CD
⇒ AB bisects CD
![]()
Question 4.
l and m are two parallel lines inter-sected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.
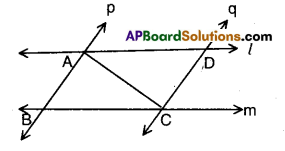
Solution:
Given that l // m; p // q.
In ΔABC and ΔCDA
∠BAC = ∠DCA (∵ alternate interior angles)
∠ACB = ∠CAD
AC = AC
∴ ΔABC ≅ ΔCDA (∵ ASA congruence)
Question 5.
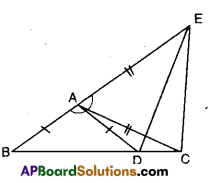
In the figure given below AC = AE; AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Solution:
Given that AC = AE, AB = AD and
∠BAD = ∠EAC
In ΔABC and ΔADE
AB = AD
AC = AE
∠BAD = ∠EAC
∴ ΔABC ≅ ΔADE (∵ SAS congruence)
⇒ BC = DE (CPCT)
![]()
Question 6.
In right triangle ABC, right angle is at ‘C’ M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that
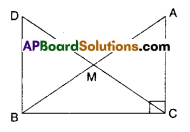
i) ΔAMC = ΔBMD
ii) ∠DBC is a right angle
iii) ΔDBC = ΔACB
iv) CM = \(\frac{1}{2}\) AB
Solution:
Given that ∠C = 90°
M is mid point of AB;
DM = CM (i.e., M is mid point of DC)
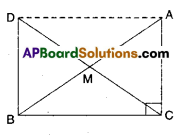
i) In ΔAMC and ΔBMD
AM = BM (∵ M is mid point of AB)
CM = DM ( ∵ M is mid point of CD)
∠AMC = ∠BMD ( ∵ Vertically opposite angles)
∴ ΔAMC ≅ ΔBMD
(∵ SAS congruence)
![]()
ii) ∠MDB = ∠MCA
(CPCT of ΔAMC and ΔBMD)
But these are alternate interior angles for the lines DB and AC and DC as transversal.
∴DB || AC
As AC ⊥ BC; DB is also perpendicular to BC.
∴ ∠DBC is a right angle.
iii) In ΔDBC and ΔACB
DB = AC (CPCT of ΔBMD and ΔAMC)
∠DBC = ∠ACB = 90°(already proved)
BC = BC (Common side)
∴ ΔDBC ≅ ΔACB (SAS congruence rule)
iv) DC = AB (CPCT of ΔDBC and ΔACB)
\(\frac { 1 }{ 2 }\) DC = \(\frac { 1 }{ 2 }\) AB (Dividing both sides by 2)
CM = \(\frac { 1 }{ 2 }\)AB
Question 7.
In the given figure ΔBCD is a square and ΔAPB is an equilateral triangle.
Prove that ΔAPD ≅ ΔBPC.
[Hint: In ΔAPD and ΔBPC; \(\overline{\mathbf{A D}}=\overline{\mathbf{B C}}\), \(\overline{\mathbf{AP}}=\overline{\mathbf{BP}}\) and ∠PAD = ∠PBC = 90° – 60° = 30°]
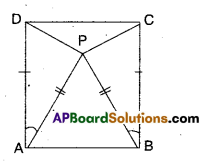
Solution:
Given that □ABCD is a square.
ΔAPB is an equilateral triangle.
Now in ΔAPD and ΔBPC
AP = BP ( ∵ sides of an equilateral triangle)
AD = BC (∵ sides of a square)
∠PAD = ∠PBC [ ∵ 90° – 60°]
∴ ΔAPD ≅ ΔBPC (by SAS congruence)
![]()
Question 8.
In the figure given below ΔABC is isosceles as \(\overline{\mathbf{A B}}=\overline{\mathbf{A C}} ; \overline{\mathbf{B A}}\) and \(\overline{\mathbf{CA}}\) are produced to Q and P such that \(\overline{\mathbf{A Q}}=\overline{\mathbf{AP}}\). Show that \(\overline{\mathbf{PB}}=\overline{\mathbf{QC}}\) .
(Hint: Compare ΔAPB and ΔACQ)
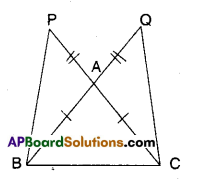
Solution:
Given that ΔABC is isosceles and
AP = AQ
Now in ΔAPB and ΔAQC
AP = AQ (given)
AB = AC (given)
∠PAB = ∠QAC (∵ Vertically opposite angles)
∴ ΔAPB ≅ ΔAQC (SAS congruence)
∴ \(\overline{\mathbf{PB}}=\overline{\mathbf{QC}}\) (CPCT of ΔAPB and ΔAQC)
![]()
Question 9.
In the figure given below AABC, D is the midpoint of BC. DE ⊥ AB, DF ⊥ AC and DE = DF. Show that ΔBED ≅ AΔCFD.
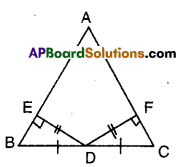
Solution:
Given that D is the mid point of BC of ΔABC.
DF ⊥ AC; DE = DF
DE ⊥ AB
In ΔBED and ΔCFD
∠BED = ∠CFD (given as 90°)
BD = CD (∵D is mid point of BC)
ED = FD (given)
∴ ΔBED ≅ ΔCFD (RHS congruence)
Question 10.
If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
Solution:
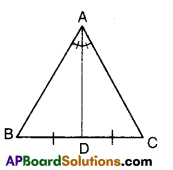
Let ΔABC be a triangle.
The bisector of ∠A bisects BC
To prove: ΔABC is isosceles
(i.e., AB = AC)
We know that bisector of vertical angle divides the base of the triangle in the ratio of other two sides.
∴ \(\frac{\mathrm{AB}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{BC}}\)
Thus \(\frac{\mathrm{AB}}{\mathrm{AC}}\) = 1( ∵ given)
⇒ AB = AC
Hence the Triangle is isosceless.
![]()
Question 11.
In the given figure ΔABC is a right triangle and right angled at B such that ∠BCA = 2 ∠BAC. Show that the hypotenuse AC = 2BC.
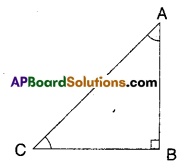
[Hint : Produce CB to a point D that BC = BD]
Solution:
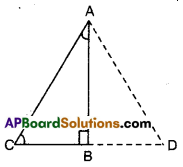
Given that ∠B = 90°; ∠BCA = 2∠BAC
To prove : AC = 2BC
Produce CB to a point D such that
BC = BD
Now in ΔABC and ΔABD
AB = AB (common)
BC = BD (construction)
∠ABC =∠ABD (∵ each 90°)
∴ ΔABC ≅ ΔABD
Thus AC = AD and ∠BAC = ∠BAD = 30° [CPCT]
[ ∵ If ∠BAC = x then
∠BCA = 2x
x + 2x = 90°
3x = 90°
⇒ x = 30°
∴ ∠ACB = 60°]
Now in ΔACD,
∠ACD = ∠ADC = ∠CAD = 60°
∴∠ACD is equilateral ⇒ AC = CD = AD
⇒ AC = 2BC (∵ C is mid point)