AP State Syllabus AP Board 9th Class Maths Solutions Chapter 12 Circles InText Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 12th Lesson Circles InText Questions
Activity
Question
Let us now do the following activity. Mark a point on a sheet of paper. Taking this point as centre draw a circle with any radius. Now increase or decrease the radius and.again draw some more circles with the same centre. What do you call the circles obtained in this activity ?[Page No. 261]
Circles having a common centre are called concentric circles.
Do This
Question 1.
In the figure which circles are congruent to the circle A ?
[Page No. 262]
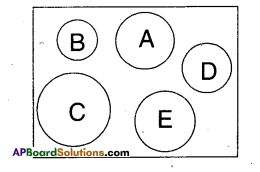
Solution:
Circle ‘E’ is congruent to circle A.
Question 2.
What measure of the circles make them congruent ? [Page No. 262]
Solution:
Radius of circles determines their congruency.
Activity
Take a thin circular-sheet and fold it to half and open. Again fold it along any other half and open. Repeat this activity for several times. Finally when you open it, what do you observe?
[Page No. 262]
Solution:
Student Activity.
Activity
Take a circular paper. Fold it along any diameter such that the two edges coincide with each other. Now open it and again fold it into half along another diameter. On open¬ing, we find two diameters meet at the centre ‘O’. There forms two pairs of vertically opposite angles which are equal. Name the end points of the diameter as A, B, C and D.
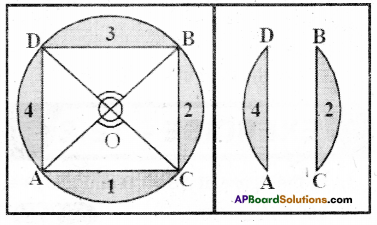
Draw the chords \(\overline{\mathrm{AC}}, \overline{\mathrm{BC}}, \overline{\mathrm{BD}}\) and \(\overline{\mathrm{AD}}\).
Now take cut-out of the four segments namely 1, 2, 3 and 4.
If you place these segments pair wise one above the other the edges of the pairs (1,3) and (2.4) coincide with each other.
Is \(\overline{\mathrm{AD}}=\overline{\mathrm{BC}}\) and \(\overline{\mathrm{AC}}=\overline{\mathrm{BD}}\) ?
Though you have seen it in this par¬ticular case, try it out for other equal angles too. The chords will all turn out to be equal because of the following theorem. [Page No. 265]
Activity
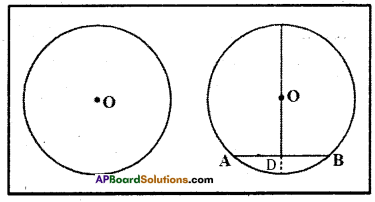
Take a circle shaped paper and mark centre ‘O’: Fold it into two unequal parts and open it. Let the crease represent a chord AB, and then make a fold such that ‘A’ coincides with B. Mark the point of intersection of the two folds as D. Is AD = DB?
∠ODA = ?; ∠ODB = ?. Measure ‘the angles between the creases. They are right- angles. So. we can make a hypothesis “the line drawn through the centre of a circle to bisect a chord is perpendicular to the chord”.
[Page No. 267]
Try This
In a circle with centre ‘O’, \(\overline{\mathbf{A B}}\) is a chord and M is its midpoint. Now prove that \(\overline{\mathbf{O M}}\) is perpendicular to AB.
(Hint : Join OA and OB consider tri-angles OAM and OBM)
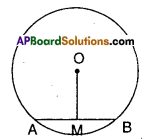[Page No. 267]
Solution:
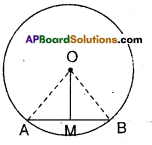
‘O’ is the centre of the circle.
AB is a chord, M is its midpoint.
Join A, B to’O’.
Now in ΔOMA and ΔOMB
OA = OB (radii)
OM = OM (common)
MA = MB (given)
∴ ΔOMA s ΔOMB (SSS congruence)
∴ ∠OMA = ∠OMB (C.P.C.T)
But ∠OMA and ∠OMB are linear pair
∴∠OMA = ∠OMB = 90°
i.e., OM ⊥ AB.
Question
If three points are eollinear, how many circles can be drawn through these points ? Now try to draw a circle passing through these, three points.
[Page No. 268]
Solution:
If three points are eollinear, we can’t draw a circle passing’ through these points.
Activity
Draw a big circle on a paper and take a cut-out of it. Mark its centre as ‘O’. Fold it in half. Now make another fold near semi-circular edge. Now unfold it. You will get two congruent folds of chords. Name them as AB and CD. Now make perpendicular folds pass¬ing through centre ‘O’ for them. Using di¬vider compare the perpendicular distances of these chords from the centre.
Repeat the above activity by folding congruent chords. State your observations as a hypothesis.
“The congruent chords in a circle are at equal distance from the centre of the circle”. [Page No. 269]
Try This
In the figure, O is the centre of the circle and AB = CD. OM is perpen-dicular on \(\overline{\mathbf{A B}}\) and \(\overline{\mathbf{O N}}\) is perpen-dicular on \(\overline{\mathbf{C D}}\). Then prove that OM = ON. [Page No. 269]
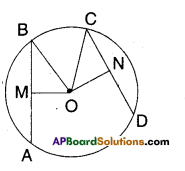
Solution:
O’ is the centre of the circle.
Chords AB = CD
OM ⊥ AB; ON ⊥ CD
In ΔOMB and ΔONC
OB = OC [∵ radii]
BM = CN \(\left[\because \frac{1}{2} \mathrm{AB}=\frac{1}{2} \mathrm{CD}\right]\)
∠OMB = ∠ONC [ ∵90° each]
∴ ΔOMB ≅ ΔONC [R.H.S congruence]
∴ OM = ON (CPCT)
Activity
Take a circle paper. Mark four points A, B, C and D on the circle paper. Draw cyclic quadrilateral ABCD and measure its angles and record it in the table. Repeat this activity for three more times
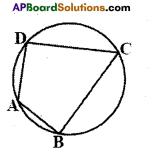
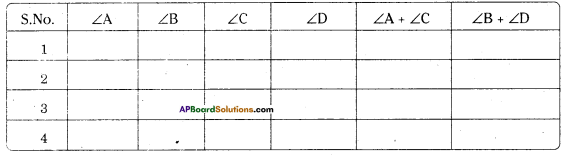
What do you infer from the table ?
Solution:
Student Activity