AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 3 Polynomials Optional Exercise Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 3rd Lesson Polynomials Optional Exercise
10th Class Maths 3rd Lesson Polynomials Optional Exercise Textbook Questions and Answers
Question 1.
Verify that the numbers given along-side the cubic polynomials below are their zeroes. Also verify the relation-ship between the zeroes and the coefficients in each case:
i) 2x3 + x2 – 5x + 2; (\(\frac{1}{2}\), 1,-2)
ii) x3 + 4x2 + 5x – 2 ; (1, 1, 1)
Answer:
i) Given polynomial 2x3 + x2 – 5x + 2
Comparing the given polynomial with ax3 + bx2 + cx + d,
we get a = 2, b = 1, c = – 5 and d = 2
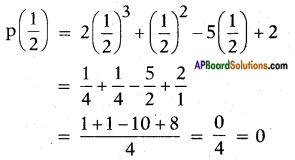
P(1) = 2(1)3 + (1)2 – 5(1) – 2
= 2 + 1 – 5 + 2 = 0
p(-2) = 2(-2)3 + (-2)2 – 5(-2) + 2
= 2(-8) + 4 + 10 + 2
= – 16 + 16 = 0
∴ \(\frac{1}{2}\), 1 and – 2 are the zeroes of 2x3 + x2 – 5x + 2
So, α = \(\frac{1}{2}\), β = 1 and γ = – 2 Therefore,
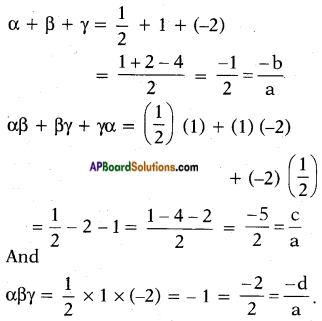
![]()
ii) Given polynomial x3 + 4x2 + 5x – 2
Comparing the given polynomial with ax3 + bx2 + cx + d,
we get a = 1, b = 4, c = 5 and d = – 2.
Given zeroes are (1, 1, 1)
p(1) = (1)3 + 4(1)2 + 5(1) – 2
= 1 + 4 + 5 – 2
= 10 – 2 = 8
∴ (1, 1, 1) are not zeroes of the given polynomial p(x).
Question 2.
Find a cubic polynomial with the sum, sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, -14 respectively.
Answer:
Let the cubic polynomial be
ax3 + bx2 + cx + d, and its zeroes be α, β and γ.
Then,
α + β + γ = 2 = \(\frac{-(-2)}{1}\) = \(\frac{-b}{a}\)
αβ + βγ + γα = -7 = \(\frac{-7}{1}\) = \(\frac{c}{a}\)
αβγ = – 14 = \(\frac{-14}{1}\) = \(\frac{-d}{a}\)
a = 1, then b = -2, c = -7 and d = 14.
So, one cubic polynomial which satisfies the given conditions will be x3 – 2x2 – 7x + 14.
Question 3.
If the zeroes of the polynomial x3 – 3x2 + x + 1 are a – b, a, a + b, find a and b.
Answer:
Given polynomial x3 – 3x2 + x + 1
Since, (a – b), a, (a + b) are the zeroes of the polynomial x3 – 3x2 + x + 1.
Therefore, sum of the zeroes
= (a – b) + a + (a + b) = \(\frac{-(-3)}{1}\) = 3
So, 3a = 3 ⇒ a = 1
∴ Sum of the products of its zeroes taken two at a time.
= a(a – b) + a(a + b) + (a + b) (a – b) = \(\frac{1}{1}\) = 1
⇒ a2 – ab + a2 + ab + a2 – b2 = 1
⇒ 3a2 – b2 = 1
So, 3(1)2 – b2 = 1 ⇒ 3 – b2 = 1
⇒ b2 = 2
⇒ b = √2 = ± √2
Here, a = 1 and b = ± √2
![]()
Question 4.
If two zeroes of the polynomial x4 – 6x3 – 26x2 + 138x – 35 are 2 ± √3 , find other zeroes.
Answer:
Let the other, two zeroes are α, β.
Then the sum of zeroes of given polynomial = 2 + √3 + 2 – √3 + α + β
= \(\frac{-b}{a}\) = \(\frac{-(-6)}{1}\) = 6
4 + α + β = 6
⇒ α + β = 2 ….. (1)
Now product of zeroes is
(2 + √3 ) (2 – √3) (α) (β)= \(\frac{e}{a}\) = \(\frac{-35}{1}\)
(4 – 3) (αβ) = – 35
⇒ αβ = – 35 …… (2)
Now (α – β)2 = (α + β)2 – 4αβ
= (2)2 – 4(-35) = 4 + 140 = 144
⇒ (α – β) = ± 12 ….. (3)
Now solving (1) & (3) we get

⇒ α = 7; then α + β = 7 + β = 2
⇒ β = -5
The remaining zeroes are α, β
= 7, -5
So total zeroes of given polynomial are 2 + √3, 2 – √3, 7, – 5.
![]()
Question 5.
If the polynomial x4 – 6x3 – 16x2 + 25x + 10 is divided by another polynomial x2 – 2x + k, the remainder comes out to be x + a, find k and a.
Answer:
Given polynomial x4 – 6x3 – 16x2 + 25x + 10 and another polynomial is x2 – 2x + k.
Remainder is x + a
Let us divide
x4 – 6x3 – 16x2 + 25x + 10 by x2 – 2x + k

∴ Remainder
= x(4k + 25 – 2k – 48) + 10 + k(k + 24)
= x(2k – 23) + (k2 + 24k + 10)
Given remainder is x + a
on comparing the coefficients of x and constant terms on both sides
2k – 23 = 1 ……. (1)
2k = 1 + 23 = 24
⇒ k = \(\frac{24}{2}\) = 12
k2 + 24k + 10 = a …….. (2)
Substitute ‘k’ value in equation (2)
(12)2 + 24(12) + 10 = a
144 + 288 + 10 = a
⇒ a = 442
∴ Required k = 12 and ‘a’ = 442