AP State Syllabus AP Board 9th Class Maths Solutions Chapter 6 Linear Equation in Two Variables Ex 6.4 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 6th Lesson Linear Equation in Two Variables Exercise 6.4
Question 1.
Give the graphical representation of the following equation
a) on the number line and b) on the Cartesian plane.
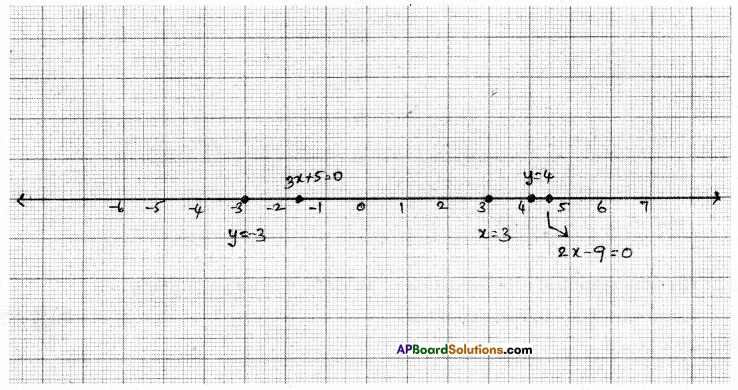
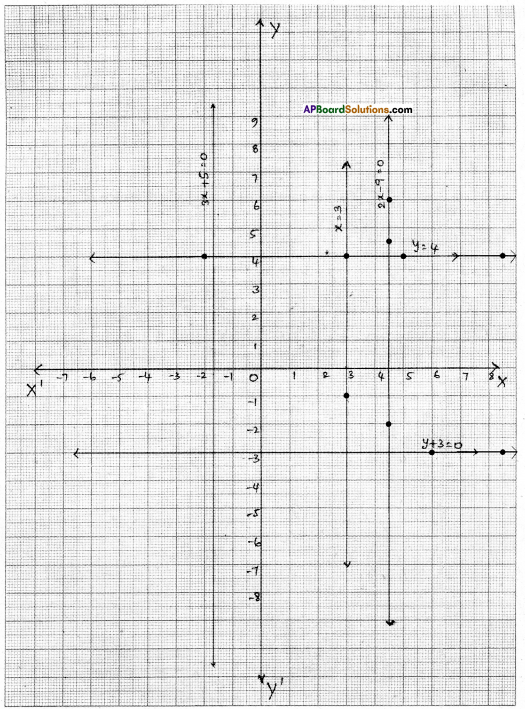
l) x = 3
ii) y + 3 = 0
iii) y = 4
iv) 2x – 9 = 0
v) 3x + 5 = 0
Solution:
i) x = 3 is a line parallel to Y-axis at a distance of 3 units on the right side of the origin.
ii) y + 3 = 0 y = – 3 is a line parallel to X-axis, below the origin.
iii) y = 4 is a line parallel to X-axis at a distance of 4 units above the origin.
iv) 2x – 9 = 0
⇒ x = \(\frac{9}{2}\) = 4.5 is a line parallel to Y-axis at a distance of 4.5 units, right side of the zero.
v) 3x + 5 = 0
⇒ 3x = -5 x = \(\frac{-5}{3}\) is a line parallel to Y – axis at a distance of \(\frac{5}{3}\)units on the left side of the origin.
x = 3
| x | 3 | 3 | 3 |
| y | -1 | 2 | 4 |
y + 3 = 0
| X | -4 | 6 | 8 |
| y | -3 | -3 | -3 |
y = 4
| x | -2 | 3 | 5 | 8 |
| y | 4 | 4 | 4 | 4 |
2x – 9 = 0
| X | 4.5 | 4.5 | 4.5 |
| y | -2 | 4 | 6 |
3x + 5 = 0
| x | \(\frac{-5}{3}\) | \(\frac{-5}{3}\) | \(\frac{-5}{3}\) |
| y | -1 | 2 | 4 |
![]()
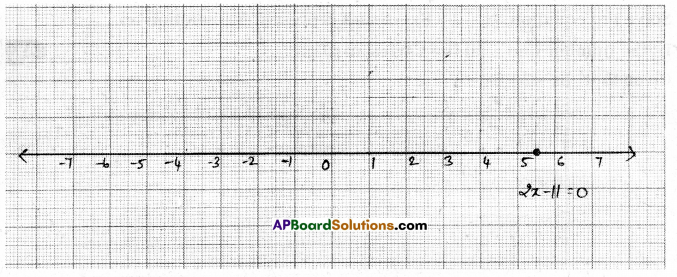
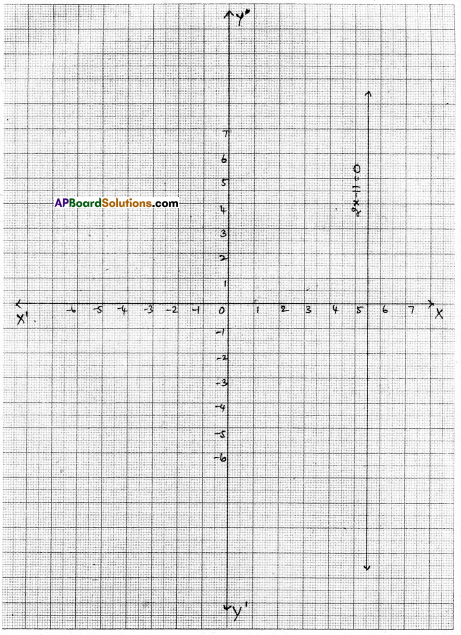
Question 2.
Give the graphical representation of 2x – 11 = 0 as an equation in i) one variable ii) two variables
Solution:
2x – 11 = 0
| x | 5.5 | 5.5 | 5.5 |
| y | -3 | 1 | 5 |
Question 3.
Solve the equation 3x + 2 = 8x – 8 and represent the solution on
i) the number line ii) the Cartesian plane.
Solution:
Given that 3x + 2 = 8x – 8
3x – 8x = – 8 – 2
– 5x = -10
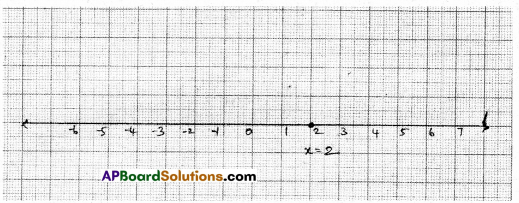
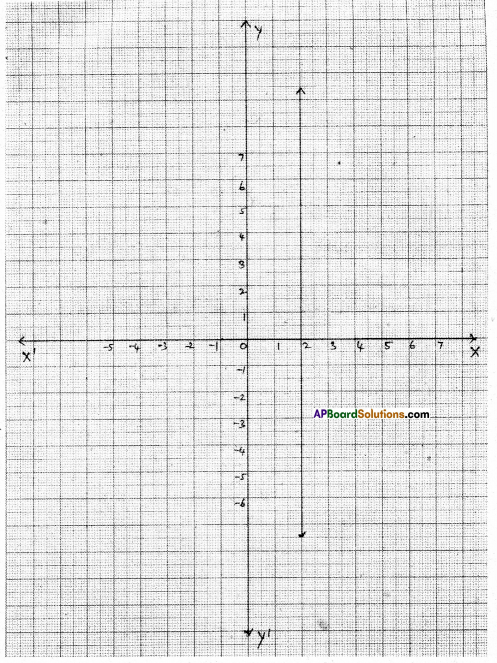
x = \(\frac{-10}{-5}\) = 2
| X | 2 | 2 | 2 |
| y | 5 | 6 | 4 |
![]()
Question 4.
Write the equation of the line parallel to X-axis and passing through the point i) (0, – 3) ii) (0,4) iii) (2, – 5) iv) (3,4)
Solution:
i) The given point is (0, – 3)
Equation of a line parallel to X-axis is y = k
∴ Required equation is y = – 3 or y + 3 = 0
ii) The given point is (0, 4)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = 4ory-4 = 0
iii) The given point is (2, – 5)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = -5 or y + 5 = 0
iv) The given point is (3, 4)
Equation of a line parallel to X-axis is y = k
∴ Required equation isy = 4 or y – 4 = 0
Question 5.
Write the equation of the line parallel to Y-axis passing through the point
i) (- 4, 0)
ii) (2,0)
iii) (3, 5)
(iv) (- 4, – 3)
Solution:
Equation of a line parallel to Y-axis is x = k
∴ The required equations are
i) Through the point (- 4, 0) ⇒ the equation is x = – 4 or x + 4 = 0
ii) Through the point (2, 0) ⇒ the equation isx = 2orx-2 = 0
iii) Through the point (3, 5) ⇒ the equation isx = 3orx-3 = 0
iv) Through the point (- 4,-3) ⇒ the equation is x = – 4 or x + 4 = 0
![]()
Question 6.
Write the equation of three lines that are
1) Parallel to the X-axis
Solution:
y = 3
y = -4
y = 6
ii) Parallel to the Y-axis
Solution:
x = – 2
x = 3
x = 4