AP State Syllabus AP Board 9th Class Maths Solutions Chapter 9 Statistics Ex 9.2 Textbook Questions and Answers.
AP State Syllabus 9th Class Maths Solutions 9th Lesson Statistics Exercise 9.2
![]()
Question 1.
Weights of parcels in a transport office are given below.

Find the mean weight of the parcels.
Solution:
| Weight in kg xi | No. of parcels fi | x1fi |
| 50 | 25 | 1250 |
| 65 | 34 | 2210 |
| 75 | 38 | 2850 |
| 90 | 40 | 3600 |
| 110 | 47 | 5170 |
| 120 | 16 | 1920 |
Σfi = 200
Σfixi = 17000
\(\begin{array}{l}
\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{17000}{200}=\frac{170}{2} \\
\overline{\mathrm{x}}=85
\end{array}\)
Mean = 85
![]()
Question 2.
Number of familles In a village in correspondence with the number of children are given below.

Find the mean number of children per family.
Solution:
| No. of childrens xi | No. of families fi | x1fi |
| 0 | 11 | 0 |
| 1 | 25 | 25 |
| 2 | 32 | 64 |
| 3 | 10 | 30 |
| 4 | 5 | 20 |
| 6 | 1 | 5 |
Σfi = 84
Σfixi = 144
\(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{144}{84}\)
Mean = 1.714285
Question 3.
If the mean of the following frequency distribution is 7.2, find value of ‘k’.

Solution:

Σfi = 40 + k;
Σfixi = 260 + 10k
Given that \(\overline{\mathrm{x}}\) = 7.2
But \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{1} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
7.2 = \(\frac{260+10 k}{40+k}\)
288.0 + 7.2k = 260 + 10k
10k – 7.2k = 288 – 260
2.8k = 28
k = \(\frac{28}{2.8}\) = 10
![]()
Question 4.
Number of villages with respect to their population as per India census 2011 are given below.

Find the average population in each village.
Solution:
| Population (in thousands xi) | Villages fi | x1fi |
| 12 | 20 | 240 |
| 5 | 15 | 75 |
| 30 | 32 | 960 |
| 20 | 35 | 700 |
| 15 | 36 | 540 |
| 8 | 7 | 56 |
Σfi = 145 Σfixi = 2571 thousands
\(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
Mean = \(\frac{2571}{145}\) = 17.731 thousands
Question 5.
A FLATOUN social and financial educational programme initiated savings programme among the high school children in Hyderabad district. Mandal wise savings in a month are given in the following table.
| Mandal | No. of schools | Total amount saved (in rupees |
| Amberpet | 6 | 2154 |
| Thirumalgiri | 6 | 2478 |
| Saidabad | 5 | 975 |
| Khairathabad | 4 | 912 |
| Secunderabad | 3 | 600 |
| Bahadurpura | 9 | 7533 |
Find arithmetic mean of school wise savings in each mandal. Also find the arithmetic mean of saving of all schools.
Solution:
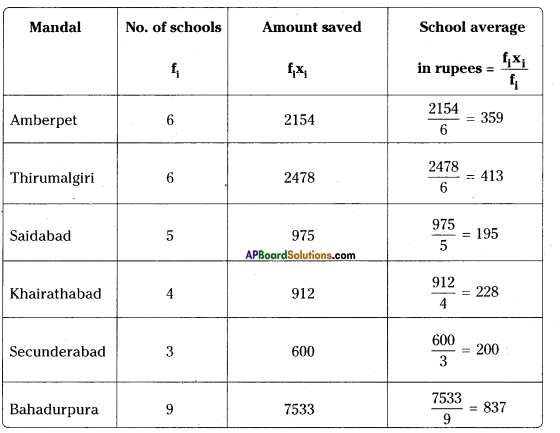
Σfi = 33
Σfixi = 14652
Mean = \(\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}\)
\(\bar{x}=\frac{14652}{33}\) = ₹ 444 (Mean savings per school)
![]()
Question 6.
The heights of boys and girls of IX class of a school are given below.

Compare the heights of the boys and girls.
[Hint: Fliid median heights of boys and girls]
Solution:
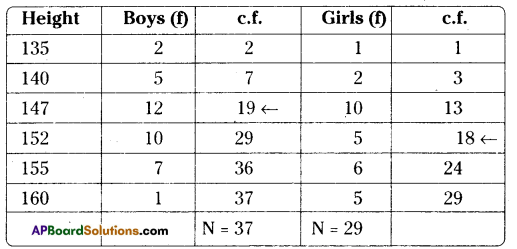
Boys median class =\(\frac{37+1}{2}=\frac{38}{2}\)= 19th observation
∴ Median height of boys = 147 cm
Girls median class = \(\frac{29+1}{2}=\frac{30}{2}\) = 15th observation
∴ Median height of girls = 152 cm
Question 7.
Centuries scored and number of cricketers in the world are given below.

Find the mean, median and mode of the given data.
Solution:
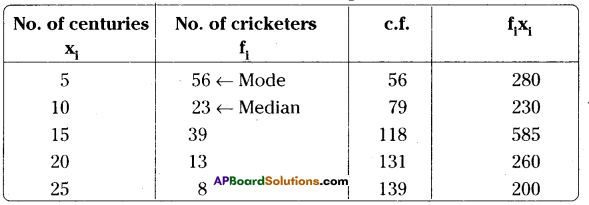
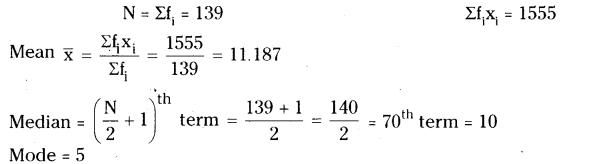
Question 8.
On the occasion of New year’s day a sweet stall prepared sweet packets. Number of sweet packets and cost of each packet is given as follows

Find the mean, median and mode of the given data.
Solution:
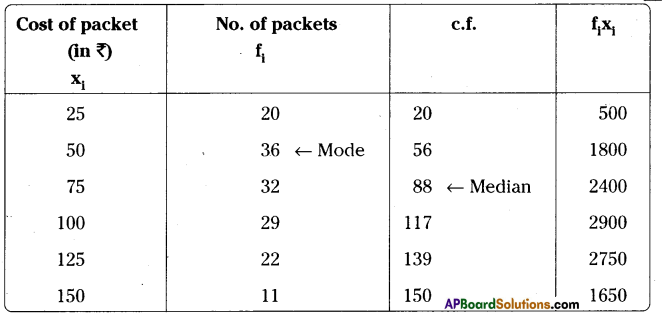
N = Σfi = 150
Σfixi = 12000
Mean = \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{12000}{150}=80\)
Median = average of (\(\frac{N}{2}+1\) and \(\frac{N}{2}\) terms = average of 75 and 76 observation = 75
Mode = 50
![]()
Question 9.
The mean (average) weight of three students is 40 kg. One of the students Ranga weighs 46 kg. The other two students, Rahim and Reshma have the same weight.
Find Rahim’s weight. cgigB)
Solution:
Weight of Ranga = 46 kg
Weight of Reshma = Weight of Rahim = x kg say
Average = \(\frac{\text { Sum of the weights }}{\text { Number }}\) = 40kg
∴ 40 = \(\frac{46+x+x}{3}\)
3 x 40 = 46 + 2x
2x = 120 – 46 = 74
∴ x = \(\frac{74}{2}\) = 37 .
∴ Rahim’s weight = 37 kg.
![]()
Question 10.
The donations given to an orphanage home by the students of different classes of a secondary school are given below.
| Class | Donation by each student in (Rs) | No. of students donated |
| VI | 5 | 15 |
| VII | 7 | 15 |
| VIII | 10 | 20 |
| IX | 15 | 16 |
| X | 20 | 14 |
Find the mean, median and mode of the data.
Solution:
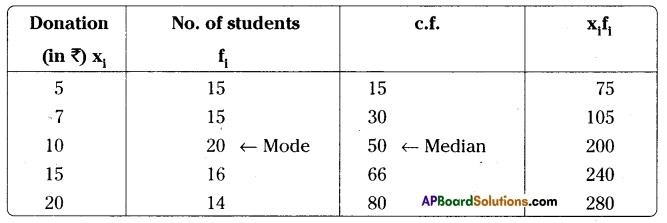
Σfi = 80
Σfixi = 900
Mean \(\overline{\mathrm{x}}=\frac{\Sigma \mathrm{f}_{\mathrm{i}} \mathrm{x}_{\mathrm{i}}}{\Sigma \mathrm{f}_{\mathrm{i}}}=\frac{900}{80}=11.25\)
Median = Average of \(\left(\frac{\mathrm{N}}{2}\right)\) and \(\left(\frac{\mathrm{N}}{2}+1\right)\) terms of \(\frac{80}{2},\left(\frac{80}{2}+1\right)\) terms
= average of 40 and 41 terms = ₹10
Mode = ₹ 10
Question 11.
There are four unknown numbers. The mean of the first two numbers is 4 and the mean of the first three is 9. The mean of all four numbers is 15; if one of the four numbers is 2 find the other numbers.
Solution:
We know that mean = \(\frac{\text { sum }}{\text { number }}\)
Given that, Mean of 4 numbers = 15
⇒ Sum of the 4 numbers = 4 x 15 = 60
Mean of the first 3 numbers = 9
⇒ Sum of the first 3 numbers = 3 x 9 = 27
Mean of the first 2 numbers = 4
⇒ Sum of the first 2 numbers = 2 x 4 = 8
Fourth number = sum of 4 numbers – sum of 3 numbers = 60 – 27 = 33
Third number = sum of 3 numbers – sum of 2 numbers = 27 – 8 = 19
Second number = Sum of 2 numbers – given number = 8-2 = 6
∴ The other three numbers are 6, 19, 33.