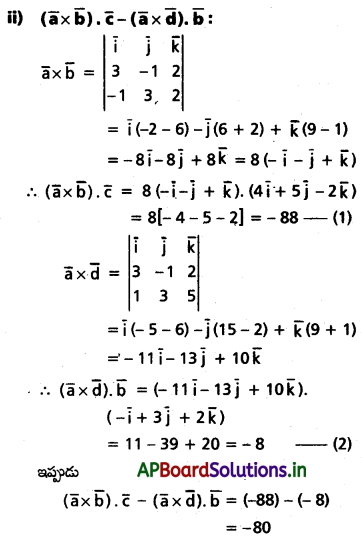AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Ex 5(b)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 5 సదిశల గుణనం Exercise 5(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 5 సదిశల గుణనం Exercise 5(b)

I.

Question 1.
\(|\overline{\mathbf{p}}|\) = 2, \(|\overline{\mathbf{q}}|\) = 3, \((\bar{p}, \bar{q})=\frac{\pi}{6}\) అయితే, \(|\overline{\mathbf{p}} \times \overline{\mathbf{q}}|^2\) ని కనుక్కోండి.
Solution:

Question 2.
\(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}-\mathbf{3} \overline{\mathbf{j}}-5 \overline{\mathbf{k}}\) అయితే, \(|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\) ని కనుక్కోండి. [Mar. ’13]
Solution:

Question 3.
\(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}-3 \overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}+4 \overline{\mathbf{j}}-2 \overline{\mathbf{k}}\) అయితే, \((\overline{\mathbf{a}}+\overline{\mathbf{b}}) \times(\overline{\mathbf{a}}-\overline{\mathbf{b}})\) ని కనుక్కోండి.
Solution:

Question 4.
\(4 \overline{\mathbf{i}}+\frac{2 \mathbf{p}}{3} \overline{\mathbf{j}}+\mathbf{p} \overline{\mathbf{k}}\), సదిశ \(\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}\) కు సమాంతరం అయితే, p విలువను కనుక్కోండి. [Mar. ’11]
Solution:

Question 5.
\(\overline{\mathbf{a}} \times(\overline{\mathbf{b}}+\overline{\mathbf{c}})+\overline{\mathbf{b}} \times(\overline{\mathbf{c}}+\overline{\mathbf{a}})+\overline{\mathbf{c}} \times(\overline{\mathbf{a}}+\overline{\mathbf{b}})\) ని గణన చేయండి.
Solution:

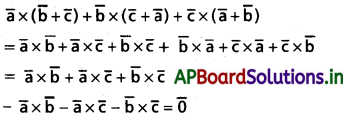
Question 6.
\(\overline{\boldsymbol{p}}=\mathbf{x} \overline{\mathbf{i}}+\mathbf{y} \overline{\mathbf{j}}+\mathbf{z} \overline{\mathbf{k}}\) అయితే, \(|\overline{\mathbf{p}} \times \overline{\mathbf{k}}|^2\) విలువను కనుక్కోండి.
Solution:

Question 7.
\(2 \bar{j} \times(3 \overline{\mathbf{i}}-4 \bar{k})+(\overline{\mathbf{i}}+2 \bar{j}) \times \overline{\mathbf{k}}\) ని గణన చేయండి.
Solution:

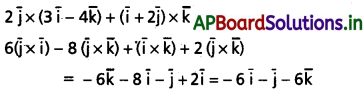
Question 8.
\(\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, 2 \overline{\mathbf{i}}+\overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) సదిశలు రెండింటికీ లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
Solution:

Question 9.
\((\overline{\mathbf{i}}+\overline{\mathbf{j}}),(\overline{\mathbf{j}}+\overline{\mathbf{k}})\) సదిశల మధ్య కోణం θ అయితే, sin θ విలువను కనుక్కోండి.
Solution:

Question 10.
\(\overline{\mathbf{a}}=\mathbf{2 j}-\overline{\mathbf{j}}, \overline{\mathbf{b}}=-\overline{\mathbf{i}}+\overline{\mathbf{k}}\) లు ఆసన్న భుజాలుగా గల సమాంతర చతుర్భుజం వైశాల్యాన్ని కనుక్కోండి.
Solution:

Question 11.
\(3 \overline{\mathbf{i}}+\overline{\mathbf{j}}-2 \overline{\mathbf{k}}, \overline{\mathbf{i}}-3 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\) లు కర్ణాలుగా గల సమాంతర చతుర్భుజం వైశాల్యాన్ని కనుక్కోండి.
Solution:

Question 12.
\(3 \bar{i}+4 \bar{j},-5 \bar{j}+7 \bar{j}\) లను రెండు భుజాలుగా కలిగిన త్రిభుజానికి వైశాల్యాన్ని కనుక్కోండి.
Solution:

Question 13.
\(\overline{\mathbf{a}}=4 \overline{\mathbf{i}}+3 \overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{b}}=2 \overline{\mathbf{i}}-6 \overline{\mathbf{j}}-3 \overline{\mathbf{k}}\) సదిశలు నిర్ధారించే తలానికి లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
Solution:

Question 14.
A(1, 2, 3), B(2, 3, 1), C(3, 1, 2) లను శీర్షాలుగా గలిగిన త్రిభుజ వైశాల్యాన్ని కనుక్కోండి. [Mar. ’14, ’06]
Solution:

II.

Question 1.
\(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}=\overline{\mathbf{0}}\) అయితే, \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{b}} \times \overline{\mathbf{c}}=\overline{\mathbf{c}} \times \overline{\mathbf{a}}\) అని నిరూపించండి.
Solution:

Question 2.
\(\overline{\mathbf{a}}=\mathbf{2} \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{b}}=-\overline{\mathbf{i}}+\mathbf{2} \mathbf{j}-4 \overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) అయితే, \((\overline{\mathbf{a}} \times \overline{\mathbf{b}}) \cdot(\overline{\mathbf{b}} \times \overline{\mathbf{c}})\) కనుక్కోండి. [(A.P) Mar. ’15]
Solution:

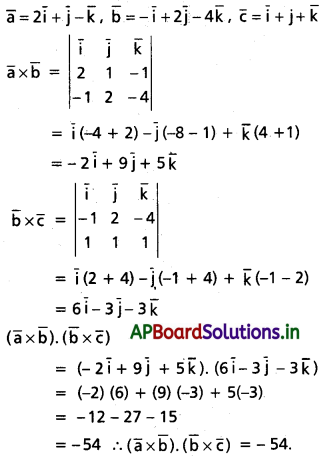
Question 3.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}-\overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}-\overline{\mathbf{j}}+\mathbf{2} \overline{\mathbf{k}}\) లు ఆసన్న భుజాలుగా గల సమాంతర చతుర్భుజం, సదిశా వైశాల్యాన్ని కనుక్కోండి.
Solution:

Question 4.
\(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{b}} \times \overline{\mathbf{c}} \neq \overline{\mathbf{0}}\) అయితే, ఏదో ఒక అదిశ p కి \(\overline{\mathbf{a}}+\overline{\mathbf{c}}=\mathbf{p} \overline{\mathbf{b}}\) అని చూపండి.
Solution:

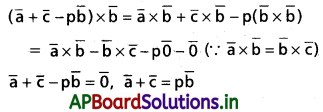
Question 5.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}\) లు \(|\overline{\mathbf{a}}|=|\overline{\mathbf{b}}|\) = 5, \((\overline{\mathbf{a}}, \overline{\mathbf{b}})\) = 45° ను తృప్తిపరచే సదిశలు అనుకుందాం. \(\bar{a}-2 \bar{b}, 3 \bar{a}+2 \bar{b}\) సదిశలను రెండు భుజాలుగా గల త్రిభుజ వైశాల్యాన్ని కనుక్కోండి. [Mar. ’07]
Solution:

Question 6.
√6 యూనిట్లు పరిమాణం కలిగి, \(\mathbf{2 i}-\overline{\mathbf{k}}\), \(3 \overline{\mathbf{i}}-\overline{\mathbf{j}}-\overline{\mathbf{k}}\) లు రెండింటికీ లంబంగా ఉండే సదిశను కనుక్కోండి.
Solution:

Question 7.
P(1, -1, 2), Q(2, 0, -1), R(0, 2, 1) బిందువులతో నిర్ణయమయ్యే తలానికి లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి.
Solution:
‘O’ మూలబిందువు అనుకుందాం.
\(\overline{\mathrm{OP}}=\overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}\)

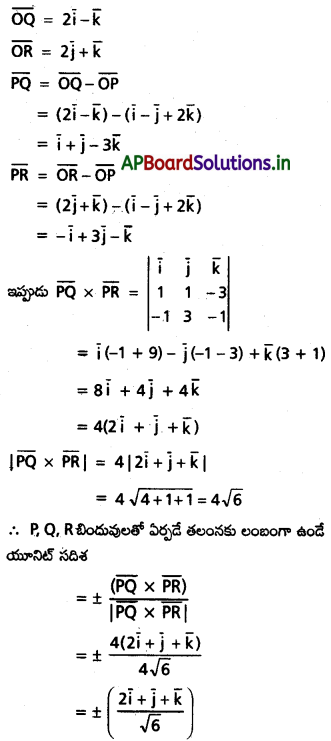
Question 8.
\(\bar{a} \cdot \bar{b}=\bar{a}, \bar{c}, \bar{a} \times \bar{b}=\bar{a} \times \bar{c}, \bar{a} \neq 0\) అయితే \(\overline{\mathbf{b}}=\overline{\mathbf{c}}\) అని చూపించండి.
Solution:

Question 9.
\(\overline{\mathbf{b}}=\mathbf{2 i}-\mathbf{2} \overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{c}}=\mathbf{2} \overline{\mathbf{i}}+\mathbf{2} \overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) సదిశలు రెండింటికీ లంబంగా ఉంటూ, మూడు పరిమాణం గల సదిశను కనుక్కోండి.
Solution:

Question 10.
\(|\overline{\mathbf{a}}|\) = 13, \(|\overline{\mathbf{b}}|\) = 5, \(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}\) = 60 అయితే, \(|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\) ని కనుక్కోండి.
Solution:
\(|\bar{a} \times \bar{b}|^2=|\bar{a}|^2|\bar{b}|^2-(\bar{a} \cdot \bar{b})^2\)
= (13)² (5)² – (60)²
= 169 × 25 – 3600
= 4225 – 3600
= 625
∴ \(|\overline{\mathbf{a}} \times \overline{\mathbf{b}}|\) = √625 = 25

Question 11.
(1, 2, 3), (2, -1, 1), (1, 2, -4) బిందువుల ద్వారా పోయే తలానికి లంబంగా ఉండే యూనిట్ సదిశను కనుక్కోండి. [Mar. ’05]
Solution:
‘O’ మూలబిందువు, A, B, C లు దత్త బిందువులు

III.

Question 1.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు త్రిభుజం ∆ABC వరుస శీర్షాలయితే, \(|(\overline{\mathbf{a}} \times \overline{\mathbf{b}})+(\overline{\mathbf{b}} \times \overline{\mathbf{c}})+(\bar{c} \times \overline{\mathbf{a}})|\) = 2(∆ABC) అని నిరూపించండి.
Solution:
‘O’ మూలబిందువు అనుకొందాం.

Question 2.
\(\overline{\mathbf{a}}=\mathbf{2 i}+\mathbf{\overline { \mathbf { j } }}+4 \overline{\mathbf{k}}, \overline{\mathbf{b}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\overline{\mathbf{i}}-\overline{\mathbf{j}}+\overline{\mathbf{k}}\) అయితే \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}} \times \bar{c})\) ని గణన చేయండి. ఈ సదిశ \(\overline{\mathbf{a}}\) కి లంబంగా ఉంటుందని సరిచూడండి.
Solution:

Question 3.
\(\overline{\mathbf{a}}=\mathbf{7 i} \overline{\mathbf{i}}-\mathbf{2} \overline{\mathbf{j}}+\mathbf{3} \overline{\mathbf{k}}, \overline{\mathbf{b}}=\mathbf{2} \overline{\mathbf{i}}+8 \overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}\) అయితే \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}, \overline{\mathbf{a}} \times \overline{\mathbf{c}}\), \(\overline{\mathbf{a}} \times(\overline{\mathbf{b}}+\overline{\mathbf{c}})\) లను గణించండి. సదిశా లబ్దం, సదిశా సంకలనంపై విభాజితం అవుతుందేమో సరిచూడండి.
Solution:

Question 4.
\(\overline{\mathbf{a}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathbf{c}}=\overline{\mathbf{j}}-\overline{\mathbf{k}}\) అయితే \(\overline{\mathbf{a}} \times \overline{\mathbf{b}}=\overline{\mathbf{c}}\) మరియు \(\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}=\mathbf{3}\) తృప్తిపరచే \(\overline{\mathbf{b}}\) కనుక్కోండి.
Solution:

Question 5.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు సమాన పరిమాణం గల సదిశలు,\(|\bar{a}+\bar{b}+\bar{c}|=\sqrt{6}\) మరియు \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లలో ప్రతి ఒక సదిశ ఇంకొక దానితో చేసే కోణం \(\frac{\pi}{3}\), అయితే \(|\bar{a}|\) విలువను కనుక్కోండి.
Solution:

Question 6.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}\) లు ఏవైనా సదిశలయితే \(\left(1+|\bar{a}|^2\right)\left(1+|\bar{b}|^2\right)\) = \(|1-\overline{\mathbf{a}} \cdot \overline{\mathbf{b}}|^2+|\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{a}} \times \overline{\mathbf{b}}|^2\) అని చూపండి.
Solution:

Question 7.
యూనిట్ సదిశలు \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) లతో \(\overline{\mathbf{a}}\) సదిశ \(\overline{\mathbf{b}}, \overline{\mathbf{c}}\) లు రెండింటికీ లంబంగా ఉండి, \(\overline{\mathbf{b}}, \overline{\mathbf{c}}\) ల మధ్య కోణం \(\frac{\pi}{3}\) అయితే, \(|\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}|\) విలువను కనుక్కోండి.
Solution:

Question 8.
\(\overline{\mathbf{a}}=3 \overline{\mathbf{i}}-\overline{\mathbf{j}}+2 \overline{\mathbf{k}}, \overline{\mathbf{b}}=-\overline{\mathbf{i}}+3 \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\), \(\overline{\mathbf{c}}=4 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}-2 \overline{\mathbf{k}}, \overline{\mathbf{d}}=\overline{\mathbf{i}}+3 \overline{\mathbf{j}}+5 \overline{\mathbf{k}}\) అయితే, ఈ కింది వాటిని గణించండి.
(i) \((\bar{a} \times \bar{b}) \times(\bar{c} \times \bar{d})\)
(ii) \((\bar{a} \times \bar{b}) \cdot \bar{c}-(\bar{a} \times \bar{d}) \cdot \bar{b}\)
Solution:
(i) \((\bar{a} \times \bar{b}) \times(\bar{c} \times \bar{d})\):
∵ \(\overline{\mathrm{a}}=3 \overline{\mathrm{i}}-\overline{\mathrm{j}}+2 \overline{\mathrm{k}}, \overline{\mathrm{b}}=-\overline{\mathrm{i}}+3 \overline{\mathrm{j}}+2 \overline{\mathrm{k}}\)