AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Ex 6(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 6 త్రికోణమితీయ నిష్పత్తులు, పరివర్తనలు Exercise 6(a)

I.

Question 1.
ఈ క్రింది వాటిని సూక్ష్మీకరించండి.
(i) tan(θ – 14π)
Solution:
tan(θ – 14π) = tan(14π – θ)
= tan(2 . (7π) – θ)
= tan θ

(ii) cot(\(\frac{21 \pi}{2}\) – θ)
Solution:
cot(\(\frac{21 \pi}{2}\) – θ) = cot(10π + (\(\frac{\pi}{2}\) – θ))
= cot(\(\frac{\pi}{2}\) – θ)
= tan θ

(iii) cosec(5π + θ)
Solution:
cosec(5π + θ) = cosec(2π + (3π + θ))
= cosec(3π + θ)
= cosec(2π + (π + θ))
= cosec (π + θ)
= -cosec θ

(iv) sec(4π – θ)
Solution:
sec(4π – θ) = sec(2π + (2π – θ))
= sec (2π – θ)
= sec θ

Question 2.
క్రింది వాటి విలువలు కనుక్కోండి.
(i) sin(-405°)
Solution:
sin (-405°) = sin(360° + 45°)
= -sin 45°
= \(-\frac{1}{\sqrt{2}}\)

(ii) cos(\(-\frac{7 \pi}{2}\))
Solution:
cos(\(-\frac{7 \pi}{2}\)) = -cos(\(\frac{7 \pi}{2}\))
= cos 630°
= cos (360° + 270°)
= -cos 270°
= cos(180° + 90°)
= -cos 90°
= 0

(iii) sec(2100°)
Solution:
sec(2100°) = sec (5 × 360° + 300°)
= sec 300°
= sec(360° – 60°)
= sec 60°
= 2

(iv) cot(-315°)
Solution:
cot(-315°) = -cot 315°
= cot(360° – 45°)
= -cot 45°
= 1

Question 3.
కింది వాటిని గణించండి.
(i) cos²45° + cos²135° + cos²225° + cos²315°
Solution:
cos²45° + cos²135° + cos²225° + cos²315°

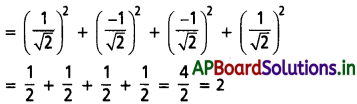
(ii) \(\sin ^2 \frac{2 \pi}{3}+\cos ^2 \frac{5 \pi}{6}-\tan ^2 \frac{3 \pi}{4}\)
Solution:
\(\sin ^2 \frac{2 \pi}{3}+\cos ^2 \frac{5 \pi}{6}-\tan ^2 \frac{3 \pi}{4}\)

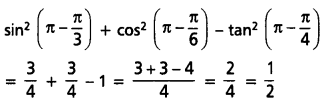
(iii) cos 225° – sin 225° + tan 495° – cot 495°
Solution:
cos(180° + 45°) – sin(180° + 45°) + tan(360° + 135°) – cot(360° + 135°)
= -cos 45° + sin 45° – tan 135° + cot 135°
= \(-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\) + 1 – 1
= 0

(iv) (a) θ = \(\frac{7 \pi}{4}\), (b) θ = \(\frac{11 \pi}{3}\) అయినప్పుడు (cos θ – sin θ) ల విలువ.
Solution:

Question 4.
(i) కోణం θ మూడో పాదంలో లేదు, sin θ = \(\frac{-1}{3}\) అయితే (a) cos θ (b) cot θ ల విలువలు కనుక్కోండి. [Mar. ’13]
Solution:
∵ sin θ = \(\frac{-1}{3}\), sin θ ఋణాత్మకం.
θ మూడవ పాదంలో లేదు.
⇒ θ నాల్గవ పాదంలో ఉంటుంది.
∴ నాల్గవ పాదంలో cos θ +ve, cot θ -ve.

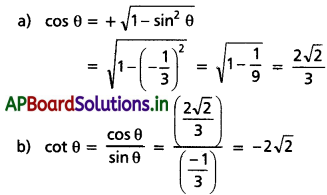
(ii) కోణం θ ఒకటో పాదం లో లేదు, cos θ = t (0 < t < 1) అయితే (a) sin θ (b) tan θ విలువలను కనుక్కోండి.
Solution:
cos θ = t, (0 < t < 1)
⇒ cos θ ధనాత్మకం
θ ఒకటవ పాదంలో లేదు.
⇒ θ నాల్గవ పాదంలో ఉంటుంది.

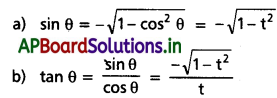
(iii) sin 330° cos 120° + cos 210° sin 300° విలువను కనుక్కోండి.
Solution:
sin 330° cos 120° + cos 210° sin 300°
= sin(360° – 30°) . cos(180° – 60°) + cos(180° + 30°) . sin(360° – 60°)
= (-sin 30°) (-cos 60°) + (-cos 30°) (-sin 60°)
= sin 30° cos 60° + cos 30° sin 60°
= sin(30° + 60°) [∵ sin A cos B + cos A sin B = sin (A + B)]
= sin(90°)
= 1

(iv) cosec θ + cot θ = \(\frac{1}{3}\), అయితే, cos θ ను కనుక్కొని θ ఏ పాదంలో ఉందో నిర్థారించండి.
Solution:
∵ cosec θ + cot θ = \(\frac{1}{3}\)
cosec θ – cot θ = 3 (∵cosec²θ – cot²θ = 1)

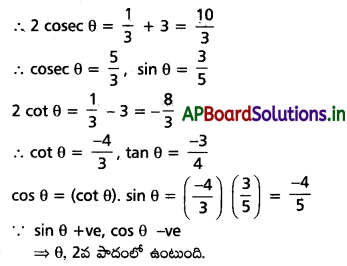
Question 5.
(i) sin α + cosec α = 2, n ∈ z అయితే sinⁿα + cosecⁿα విలువను కనుక్కోండి. [May ’13]
Solution:
ఇచ్చినది sin α + cosec α = 2
S.B.S.
sin²α + cosec²α + 2 = 4
sin²α + cosec²α = 2
sin α + cosec α = 2
C.B.S.
sin³α + cosec³α + 3 sin α . cosec α (sin α + cosec α) = 8
sin³α + cosec³α + 3(2) = 8
sin³α + cosec³α = 8 – 6
sin³α + cosec³α = 2
similarly sinⁿα + cosecⁿα = 2

(ii) sec θ + tan θ = 5 అయితే, θ ఉండే పాదాన్ని, sin θ విలువను కనుక్కోండి.
Solution:

II.

Question 1.
కింది వాటిని నిరూపించండి.
(i) \(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\)
Solution:
\(\frac{\cos (\pi-A) \cdot \cot \left(\frac{\pi}{2}+A\right) \cos (-A)}{\tan (\pi+A) \tan \left[\frac{3 \pi}{2}+A\right] \sin (2 \pi-A)}\)
= \(\frac{-\cos A(-\tan A) \cos A}{\tan A(-\cot A)\left(-\sin ^{\prime} A\right)}\)
= cos A

(ii) \(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\) = cos4A
Solution:
\(\frac{\sin (3 \pi-A) \cos \left(A-\frac{\pi}{2}\right) \tan \left(\frac{3 \pi}{2}-A\right)}{{cosec}\left(\frac{13 \pi}{2}+A\right) \sec (3 \pi+A) \cot \left(A-\frac{\pi}{2}\right)}\)

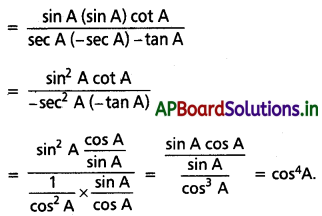
(iii) sin 780° . sin 480° + cos 240° . cos 300° = \(\frac{1}{2}\)
Solution:
sin 780° . sin 480° + cos 240° . cos 300°
= sin(2(360°) + 60°) . sin(360° + 120°) + cos(270° – 30°) . cos(360° – 60°)
= sin 60° . sin 120° – sin 30° cos 60°

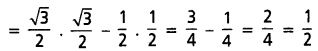
(iv) \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\) = -2
Solution:
\(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135^{\circ}+3 \sin 210^{\circ}}\)

(v) \(\cot \left(\frac{\pi}{20}\right) \cdot \cot \left(\frac{3 \pi}{20}\right) \cdot \cot \left(\frac{5 \pi}{20}\right) \cdot \cot \left(\frac{7 \pi}{20}\right)\) . \(\cot \left(\frac{9 \pi}{20}\right)\) = 1
Solution:
L.H.S = \(\cot \left(\frac{\pi}{20}\right) \cdot \cot \left(\frac{3 \pi}{20}\right) \cdot \cot \left(\frac{5 \pi}{20}\right) \cdot \cot \left(\frac{7 \pi}{20}\right)\) . \(\cot \left(\frac{9 \pi}{20}\right)\)
= cot(9°) cot(27°) cot(45°) cot(63°) cot(81°)
= cot(9°) cot(27°) (1) cot(90° – 27°) cot(90° – 9°)
= cot(9°) cot(27°) tan 27° tan 9°
= (tan 9° cot 9°) (tan 27° cot 27°)
= (1) (1)
= 1

Question 2.
(i) \(\frac{\sin \left(-\frac{11 \pi}{3}\right) \tan \left(\frac{35 \pi}{6}\right) \sec \left(-\frac{7 \pi}{3}\right)}{\cot \left(\frac{5 \pi}{4}\right) {cosec}\left(\frac{7 \pi}{4}\right) \cos \left(\frac{17 \pi}{6}\right)}\) ను సూక్ష్మీకరించండి.
Solution:
sin(\(\frac{-11 \pi}{3}\))
= sin(-660°)
= sin(-2 × 360° + 60°)
= sin 60°
= \(\frac{\sqrt{3}}{2}\)
tan(\(\frac{35 \pi}{6}\))
= tan(1050°)
= tan(3 × 360° – 30°)
= -tan 30°
= \(-\frac{1}{\sqrt{3}}\)
sec(\(-\frac{7 \pi}{3}\))
= sec(-420°)
= sec 420°
= sec(360° + 60°)
= sec 60°
= 2
cot(\(\frac{5 \pi}{4}\))
= cot(225°)
= cot(180° + 45°)
= cot 45°
= 1
cosec(\(\frac{7 \pi}{4}\))
= cosec(315°)
= cosec(270° + 45°)
= -sec 45°
= -√2
cos(\(\frac{17 \pi}{6}\))
= cos(570°)
= cos(540° – 30°)
= -cos 30°
= \(-\frac{\sqrt{3}}{2}\)

(ii) tan 20° = p అయితే, \(\frac{\tan 610^{\circ}+\tan 700^{\circ}}{\tan 560^{\circ}-\tan 470^{\circ}}=\frac{1-p^2}{1+p^2}\) అని చూపండి.
Solution:

Question 2.
α, β లు పూరక కోణాలు. b sin α = a, అయితే, sin α cos β – cos α sin β విలువను కనుక్కోండి.
Solution:
∵ α, β లు పూరక కోణాలు.
α + β = 90°
⇒ β = 90° – α
sin α cos β – cos α sin β = sin(α – β)
= sin[(α – (90° – α)]
= sin[2α – 90°]
= -sin(90° – 2α)
= -cos 2α
= -(1 – 2 sin²α) (∵ cos 2α = 1 – 2 sin²α)
= -1 + 2\(\left(\frac{a}{b}\right)^2\) [∵ sin α = \(\frac{a}{b}\) (ఇవ్వబడినది)]
= \(\frac{-b^2+2 a^2}{b^2}\)
= \(\frac{2 a^2-b^2}{b^2}\)

Question 3.
(i) A రెండో పాదం లేని కోణం, B మూడవ పాదంలో లేని కోణం, cos A = cos B = \(-\frac{1}{2}\) అయితే, \(\frac{4 \sin B-3 \tan A}{\tan B+\sin A}\) విలువను కనుక్కోండి.
Solution:
Solution:
∵ cos A = \(-\frac{1}{2}\), A రెండవ పాదంలో లేదు.
cos A -ve, కనుక
⇒ A, మూడవ పాదంలో ఉంటుంది.
cos B = \(-\frac{1}{2}\), B మూడవ పాదంలో లేదు.
cos B -ve, కనుక
⇒ B, రెండవ పాదంలో ఉంటుంది.
∵ cos A = \(-\frac{1}{2}\)
A మూడవ పాదంలో ఉంటుంది.
⇒ A = 240°
∵ cos B = \(-\frac{1}{2}\), B రెండవ పాదంలో ఉంది.
⇒ B = 120°

(ii) కోణాలు A, B లు 4వ పాదంలో లేవు, 8 tan A = -15, 25 sin B = -7 అయితే, sin A cos B + cos A sin B = \(\frac{-304}{425}\) అని చూపండి.
Solution:
8 tan A = -15 ⇒ tan A = \(\frac{-15}{8}\)
25 sin B = -7 ⇒ sin B = \(\frac{-7}{25}\)
దత్తాంశము గురించి A, Bలు నాలుగో పాదంలో ఉండవు.
∴ A రెండవ పాదంలోను B మూడవ పాదంలో ఉండాలి.
sin A cos B + cos A sin B =

(iii) A, B, C, D లు ఒక చక్రీయ చతుర్భుజం కోణాలు అయితే,
(a) sin A – sin C = sin D – sin B
(b) cos A + cos B + cos C + cos D = 0 అని చూపండి.
Solution:
∵ A, B, C, D లు చక్రీయ చతుర్భుజ కోణాలు,
⇒ A + C = 180°, B + D = 180°
⇒ C = 180° – A, D = 180° – B
(i) L.H.S. = sin A – sin C
= sin (A) – sin (180° – A)
= sin A – sin A
= 0
R.H.S. = sin D – sin B
= sin (180° – B) – sin B
= sin B – sin B
= 0
∴ L.H.S. = R.H.S.
i.e., sin A – sin C = sin D – sin B
(ii) L.H.S. = cos A + cos B + cos C + cos D
= cos A + cos B + cos (180° – A) + cos (180° – B)
= cos A + cos B – cos A – cos B
= 0
∴ cos A + cos B + cos C + cos D = 0

Question 4.
(i) a cos θ – b sin θ = c, a sin θ + b cos θ = \(\pm \sqrt{a^2+b^2-c^2}\) అని చూపండి.
Solution:
a cos θ – b sin θ = c
let a sin θ + b cos θ = x
వర్గము చేసి కూడగా
(a cos θ – b sin θ)² + (a sin θ + b cos θ)² = c² + x²
⇒ a² cos²θ + b² sin²θ – 2ab sin θ cos θ + a² sin²θ + b² cos²θ + 2ab sin θ = c² + x²
⇒ a² + b² = c² + x²
⇒ a² + b² – c² = x²
⇒ x = \(\pm \sqrt{a^2+b^2-c^2}\)
∴ a sin θ + b cos θ = \(\pm \sqrt{a^2+b^2-c^2}\)

(ii) 3 sin A + 5 cos A = 5, అయితే 5 sin A – 3 cos A = ±3 అని చూపండి.
Solution:
3 sin A + 5 cos A = 5
let 5 sec A – 3 cos A = x
ఇరువైపులా వర్గము చేసి కూడగా
(3 sin A + 5 cos A)² + (5 sin A – 3 cos A)² = 5² + x²
⇒ 9 sin²A + 25 cos²A + 30 sin A cos A + 25 sin²A + 9 cos²A – 30 sin A cos A = 25 + x²
⇒ 9 + 25 = 25 + x²
⇒ x² = 9
⇒ x = ±3
∴ 5 sin A – 3 cos A = ±3

(iii) tan²θ = (1 – e²), అయితే sec θ + tan³θ . cosec θ = \(\left(2-e^2\right)^{3 / 2}\) అని చూపండి.
Solution:
tan²θ = 1 – e²
sec²θ = 1 + tan²θ = 2 – e²
sec θ + tan³θ . cosec θ
= sec θ + \(\frac{\sin ^3 \theta}{\cos ^3 \theta} \cdot \frac{1}{\sin \theta}\)
= sec θ + \(\frac{\sin ^2 \theta}{\cos ^2 \theta} \cdot \frac{1}{\cos \theta}\)
= sec θ + tan²θ . sec θ
= sec θ (1 + tan²θ)
= sec θ . sec²θ
= \(\left(2-e^2\right) \sqrt{2-e^2}\)
= \(\left(2-e^2\right)^{3 / 2}\)

III.

Question 1.
కింది వాటిని నిరూపించండి.
(i) \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\) [Mar. ’14]
Solution:

(ii) (1 + cot θ – cosec θ) (1 + tan θ + sec θ) = 2
Solution:
L.H.S. = (1 + cot θ – cosec θ) (1 + tan θ + sec θ)

(iii) 3(sin θ – cos θ)⁴ + 6(sin θ + cos θ)² + 4(sin⁶θ + cos⁶θ) = 13
Solution:
(sin θ – cos θ)² = sin²θ + cos²θ – 2 sin θ . cos θ = 1 – 2 sin θ cos θ
(sin θ – cos θ)⁴ = (1 – 2 sin θ cos θ)² = 1 + 4 sin²θ cos²θ – 4 sin θ cos θ …….(1)
(sin θ + cos θ)² = sin²θ + cos²θ + 2 sin θ cos θ = 1 + 2 sin θ cos θ ……(2)
sin⁶θ + cos⁶θ = (sin²θ + cos²θ)³ – 3 sin²θ cos²θ (sin²θ + cos²θ) = 1 – 3 sin²θ cos²θ …….(3)
L.H.S. = 3(1 + 4 sin²θ cos²θ – 4 sin θ cos θ) + 6(1 + 2 sin θ cos θ) + 4(1 – 3 sin²θ cos²θ)
= 3 + 12 sin²θ cos²θ – 12 sin θ cos θ + 6 + 12 sin θ cos θ + 4 – 12 sin²θ cos²θ
= 3 + 6 + 4
= 13
= R.H.S.

Question 2.
కింది వాటిని నిరూపించండి.
(i) (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ) = 7
Solution:
L.H.S. = (sin θ + cosec θ)² + (cos θ + sec θ)² – (tan²θ + cot²θ)
= (sin²θ + cosec²θ + 2 sin θ cosec θ) + (cos²θ + sec²θ + 2 cos θ sec θ – (tan²θ + cot²θ)
= (sin²θ + cos²θ) + (1 + cot²θ) + (1 + tan²θ) + 4 – tan²θ – cot²θ
= 1 + 1 + 1 + 4
= 7

(ii) cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^2 \alpha}\right)\) = (1 – sin⁴α)
Solution:
L.H.S. = cos⁴α + 2 cos²α \(\left(1-\frac{1}{\sec ^2 \alpha}\right)\)
= cos⁴α + 2 cos²α (1 – cos²α)
= cos²α [cos²α + 2 sin²α]
= (1 – sin²α) [cos²α + sin²α + sin²α]
= (1 – sin²α) (1 + sin²α)
= 1 – sin⁴α

(iii) \(\frac{(1+\sin \theta-\cos \theta)^2}{(1+\sin \theta+\cos \theta)^2}=\frac{1-\cos \theta}{1+\cos \theta}\)
Solution:

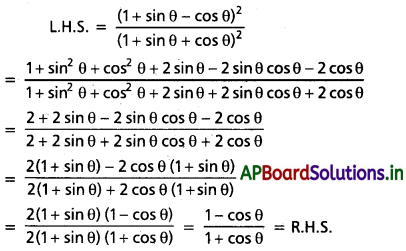
(iv) \(\frac{2 \sin \theta}{(1+\cos \theta+\sin \theta)}\) = x అయితే, \(\frac{(1-\cos \theta+\sin \theta)}{(1+\sin \theta)}\) విలువను కనుక్కోండి.
Solution:

Question 3.
కింది వాటిలో θను లోపింపచేయండి.
(i) x = a cos³θ; y = b sin³θ
Solution:

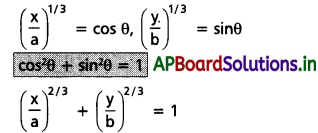
(ii) x = a cos⁴θ; y = b sin⁴θ
Solution:

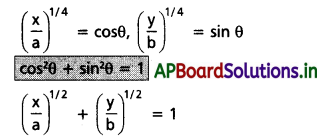
(iii) x = a(sec θ + tan θ); y = b(sec θ – tan θ)
Solution:
\(\frac{x}{a}\) = sec θ + tan θ
\(\frac{y}{b}\) = sec θ – tan θ
\(\frac{x}{a} \times \frac{y}{b}\) = (sec θ + tan θ) (sec θ – tan θ) = sec²θ – tan²θ
\(\frac{xy}{ab}\) = 1
xy = ab

(iv) x = cot θ + tan θ; y = sec θ – cos θ
Solution:
ఇచ్చినది x = cot θ + tan θ, y = sec θ – cos θ
x² = (cot θ + tan θ)²
= cot²θ + tan²θ + 2 cot θ tan θ
= cot²θ + tan²θ + 2(1)
= (1 + tan²θ) + (1 + cot²θ)
= sec²θ + cosec²θ
= \(\frac{1}{\cos ^2 \theta}+\frac{1}{\sin ^2 \theta}\)
= \(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin ^2 \theta \cos ^2 \theta}\)
= \(\frac{1}{\sin ^2 \theta \cos ^2 \theta}\)
∴ x² = sec²θ cosec²θ ……..(1)
y = (sec θ – cos θ)
y² = (sec θ – cos θ)²
y² = sec²θ + cos²θ – 2(sec θ cos θ)
= sec²θ + cos²θ – 2(1)
= (sec²θ – 1) – (1 – cos²θ)
= tan²θ – sin²θ
= sin²θ \(\left(\frac{1}{\cos ^2 \theta}-1\right)\)
= sin²θ (sec²θ – 1)
= sin²θ tan²θ ……..(2)
ఇప్పుడు x²y = (sec²θ cosec²θ) (sin θ tan θ)