AP Inter 1st Year Maths 1A Solutions Chapter 7 త్రికోణమితీయ సమీకరణాలు Ex 7(a)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 7 త్రికోణమితీయ సమీకరణాలు Exercise 7(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 7 త్రికోణమితీయ సమీకరణాలు Exercise 7(a)

I.

Question 1.
కింది సమీకరణాలకు ప్రధాన సాధనలు కనుక్కోండి.
(i) 2 cos²θ = 1
Solution:
2 cos²θ = 1
⇒ cos²θ = \(\frac{1}{2}\)
⇒ θ = 45°, 135°

(ii) √3 sec θ + 2 = 0
Solution:
√3 sec θ + 2 = 0
⇒ sec θ = \(\frac{-2}{\sqrt{3}}\)
⇒ cos θ = \(\frac{-\sqrt{3}}{2}\)
⇒ θ = 150°

(iii) 3tan²θ = 1
Solution:
3tan²θ = 1
⇒ tan²θ = \(\frac{1}{3}\)
⇒ θ = \(\pm \frac{\pi}{6}\)

Question 2.
కింది సమీకరణాలను సాధించండి.
(i) cos 2θ = \(\frac{\sqrt{5}+1}{4}\), θ ∈ [0, 2π]
Solution:

(ii) tan²θ = 1, θ ∈ [-π, +π]
Solution:
tan²θ = 1
tan θ = ±1
tan θ = ±1 = tan(±\(\frac{\pi}{4}\))
ప్రధాన సాధన θ = ±\(\frac{\pi}{4}\)
సార్వత్రిక సాధన nπ ± \(\frac{\pi}{4}\) n ∈ Z
n = -1, 0, 1 రాస్తే \(\left\{\frac{-3 \pi}{4}, \frac{-\pi}{4}, \frac{\pi}{4}, \frac{3 \pi}{4}\right\}\)
[-π, +π] అంతరంలో θ = \(\left\{\frac{-3 \pi}{4}, \frac{-\pi}{4}, \frac{\pi}{4}, \frac{3 \pi}{4}\right\}\)

(iii) sin 3θ = \(\frac{\sqrt{3}}{2}\), θ ∈ [-π, +π]
Solution:

(iv) cos²θ = \(\frac{3}{4}\), θ ∈ [0, π]
Solution:
cos²θ = \(\frac{3}{4}\)
cos θ = ±\(\frac{\sqrt{3}}{2}\)
సార్వత్రిక సాధన
θ = nπ ± \(\frac{\pi}{6}\), n ∈ Z
n = 0, 1 రాస్తే
[0, π] లో సాధనాలు θ = \(\left\{\frac{\pi}{6}, \frac{5 \pi}{6}\right\}\)

(v) 2sin²θ = sin θ, θ ∈ (0, π)
Solution:
2 sin²θ – sin θ = 0
sin θ (2sin θ – 1) = 0
sin θ = 0 మరియు sin θ = \(\frac{1}{2}\)
∵ θ ∈ (0, π)
∴ θ = \(\left\{\frac{\pi}{6}+\frac{5 \pi}{6}\right\}\)

Question 3.
కింది సమీకరణాలకు సార్వత్రిక సాధనాలను కనుక్కోండి.
(i) sin θ = \(\frac{\sqrt{3}}{2}\), cos θ = \(\frac{-1}{2}\)
Solution:

(ii) tan x = \(\frac{-1}{\sqrt{3}}\), sec x = \(\frac{2}{\sqrt{3}}\)
Solution:

(iii) cosec θ = -2, cot θ = -√3
Solution:

Question 4.
(i) sin(270° – x) = cos 292° అయితే (0°, 360°) లోని x విలువలను కనుక్కోండి.
Solution:
sin(270° – x) = cos (292°)
⇒ -cos x = cos(180° + 112°)
-cos x = -cos 112°
cos x = cos 112°
∴ x = 112° or x = 360° – 112° = 248°

(ii) x < 90°, sin (x + 28°) = cos (3x – 78°) అయితే x విలువను కనుక్కోండి.
Solution:
sin(x + 28°) = cos(3x – 78°)
= sin(90° – 3x + 78°)
= sin(168° – 3x)
x + 28° = 168° – 3x + 28° (180°) or x = 180°- (168° – 3x) + 2x (180°)
⇔ ∃ n ∈ Z అయిన
4x = 140° + 2x (180°)
2x = 16° – 2x (180°)
⇔ ∃ n ∈ Z అయిన
x = 35° + x (90°) or x = 8° – x(180°)
x = 8° మరియు x = 35° విలువలు (0, 90°) మధ్య ఉండి ఇచ్చిన సమీకరణాన్ని సంతృప్తిపరుస్తుంది.

Question 5.
కింది సమీకరణాలకు సార్వత్రిక సాధనలను రాయండి.
(i) 2 sin²θ = 3 cos θ
Solution:
2 sin²θ = 3 cos θ
2(1 – cos²θ) = 3 cos θ
⇒ 2 cos²θ + 3 cos θ – 2 = 0
⇒ 2 cos²θ + 4 cos θ – cos θ – 2 = 0
⇒ 2 cos θ (cos θ + 2) – 1(cos θ + 2) = 0
⇒ (2 cos θ – 1) (cos θ + 2) = 0
⇒ cos θ = \(\frac{1}{2}\) (లేదా) cos θ = -2
∵ cos θ వ్యాప్తి [-1, 1]
cos θ = -2 అసాధ్యం
∴ cos θ = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
ప్రధాన సాధన θ = \(\frac{\pi}{3}\)
సార్వత్రిక సాధన θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z

(ii) sin²θ – cos θ = \(\frac{1}{4}\)
Solution:
sin²θ – cos θ = \(\frac{1}{4}\)
⇒ 4(1 – cos²θ) – 4 cos θ = 1
⇒ 4 cos²θ + 4 cos θ – 3 = 0
⇒ 4 cos²θ + 6 cos θ – 2 cos θ – 3 = 0
⇒ 2 cos θ (2 cos θ + 3) – (2 cos θ + 3) = 0
⇒ (2 cos θ – 1) (2 cos θ + 3) = 0
∴ cos θ = \(\frac{1}{2}\) (లేదా) cos θ = \(\frac{-3}{2}\)
∵ cos θ వ్యాప్తి [-1, 1]
cos θ = \(\frac{-3}{2}\) అసాధ్యం
∴ cos θ = \(\frac{1}{2}=\cos \left(\frac{\pi}{3}\right)\)
ప్రధాన సాధన θ = \(\frac{\pi}{3}\)
సార్వత్రిక సాధన θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z

(iii) 5 cos²θ + 7 sin²θ = 6
Solution:
5 cos²θ + 7 sin²θ = 6
cos²θ చే భాగిస్తే,
⇒ 5 + 7 tan²θ = 6 sec²θ
⇒ 5 + 7 tan²θ = 6(1 + tan²θ)
⇒ tan²θ = 1
⇒ tan θ = ±1
∴ సార్వత్రిక సాధన θ = nπ ± \(\frac{\pi}{4}\), n ∈ Z

(iv) 3 sin⁴x + cos⁴x = 1
Solution:
3 sin⁴x + cos⁴x = 1
⇒ 3 sin⁴x + (cos²x)2 = 1
⇒ 3 sin⁴x + (1 – sin²x)2 = 1
⇒ 3 sin⁴x + 1 + sin⁴x – 2 sin²x = 1
⇒ 4 sin⁴x – 2 sin²x = 0
⇒ 2 sin²x (2 sin²x – 1) = 0
⇒ sin x = 0 (లేదా) sin x = \(\pm \frac{1}{\sqrt{2}}\)
sin x = 0
సార్వత్రిక సాధన x = nπ, n ∈ Z
sin x = \(\pm \frac{1}{\sqrt{2}}\) అయిన
సార్వత్రిక సాధన x = nπ ± \(\frac{\pi}{4}\), n ∈ Z
∴ సార్వత్రిక సాధనలు x = nπ (లేదా) nπ ± \(\frac{\pi}{4}\), n ∈ Z

II.

Question 1.
ఈ కింది సమీకరణాలను సాధించి సార్వత్రిక సాధనలను రాయండి.
(i) 2 sin²θ – 4 = 5 cos θ
Solution:
2(1 – cos²θ) – 4 = 5 cos θ
⇒ 2 – 2cos²θ – 4 = 5 cos θ
⇒ 2 cos²θ + 5 cos θ + 2 = 0
⇒ 2 cos²θ + 4 cos θ + cos θ + 2 = 0
⇒ 2 cos θ (cos θ + 2) + 1(cos θ + 2) = 0
⇒ (cos θ + 2) (2 cos θ + 1) = 0
⇒ cos θ = -2 or cos θ = \(\frac{-1}{2}\)
⇒ cos θ = -2 సాధ్యపడదు.
∴ cos θ = \(-\frac{1}{2}=\cos \frac{2 \pi}{3}\)
∴ సార్వత్రిక సాధన θ = 2nπ ± \(\frac{2\pi}{4}\), n ∈ Z

(ii) 2 + √3 sec x – 4 cos x = 2√3
Solution:
2 + \(\frac{\sqrt{3}}{\cos x}\) – 4 cos x = 2√3
⇒ \(\frac{2 \cos x+\sqrt{3}-4 \cos ^2 x}{\cos x}\) = 2√3
⇒ 2 cos x + √3 – 4 cos²x = 2√3 cos x
⇒ 4 cos²x + 2√3 cos x – 2 cos x – √3 = 0
⇒ 2 cos x (2 cos x + √3) – 1(2 cos x + √3) = 0
⇒ (2 cos x – 1) (2 cos x + √3) = 0
⇒ cos x = \(\frac{1}{2}\) or cos x = \(\frac{-\sqrt{3}}{2}\)
If cos x = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\), n ∈ Z
ప్రధాన సాధన x = 2nπ ± \(\frac{\pi}{3}\)
If cos x = \(\frac{-\sqrt{3}}{2}=\cos \frac{5 \pi}{3}\)
ప్రధాన సాధన x = 2nπ ± \(5\frac{\pi}{3}\), n ∈ Z

(iii) 2 cos²θ + 11 sin θ = 7 [May ’13]
Solution:
2 cos²θ + 11 sin θ = 7
⇒ 2(1 – sin²θ) + 11 sin θ = 7
⇒ 2 – 2 sin²θ + 11 sin θ = 7
⇒ 2 sin²θ – 11 sin θ + 5 = 0
⇒ 2 sin²θ – 10 sin θ – sin θ + 5 = 0
⇒ 2 sin θ (sin θ – 5) – 1 (sin θ – 5) = 0
⇒ (sin θ – 5) (2 sin θ – 1) = 0
⇒ sin θ = 5 or sin θ = \(\frac{1}{2}\)
If sin θ = 5 సాధ్యపడదు.
∴ sin θ = \(\frac{1}{2}=\sin \frac{\pi}{6}\)
సార్వత్రిక సాధన θ = nπ ± (-1)n \(\frac{\pi}{6}\), n ∈ Z

(iv) 6 tan²x – 2 cos²x = cos 2x
Solution:
6 tan²x – 2 cos²x = cos 2x
⇒ 6(sec²x – 1) – 2 cos²x = 2 cos²x – 1
⇒ 6 sec²x – 6 – 4 cos²x + 1 = 0
⇒ 6 sec²x – 4 cos²x – 5 = 0
⇒ \(\frac{6}{\cos ^2 x}\) – 4 cos²x – 5 = 0
⇒ 6 – 4 cos⁴x – 5 cos²x = 0
⇒ 4 cos⁴x + 5 cos²x – 6 = 0
⇒ 4 cos⁴x + 8 cos²x – 3 cos²x – 6 = 0
⇒ 4 cos²x (cos²x + 2) – 3(cos²x + 2) = 0
⇒ (4 cos²x – 3) (cos²x + 2) = 0
⇒ 4 cos²x = 3 [∵ cos²x ≠ -2]
⇒ cos x = \(\pm \frac{\sqrt{3}}{2}\)
సార్వత్రిక సాధన x = nπ ± \(\frac{\pi}{6}\), n ∈ Z

(v) 4 cos²θ + √3 = 2(√3 + 1) cos θ
Solution:
4 cos²θ + √3 = 2(√3 + 1) cos θ
⇒ 4 cos²θ – 2(√3 + 1) cos θ + √3
⇒ 4 cos²θ – 2√3 cos θ – 2 cos θ + √3
⇒ 2 cos θ (2 cos θ – √3) – 1(2 cos θ – √3) = 0
⇒ (2 cos θ – 1) (2 cos θ – √3) = 0
⇒ cos θ = \(\frac{1}{2}\) (లేదా) cos θ = \(\frac{\sqrt{3}}{2}\)
cos θ = \(\frac{1}{2}=\cos \left(\frac{\pi}{3}\right)\)
సార్వత్రిక సాధన
∴ θ = 2nπ ± \(\frac{\pi}{3}\), n ∈ Z
cos θ = \(\frac{\sqrt{3}}{2}=\cos \left(\frac{\pi}{6}\right)\)
సార్వత్రిక సాధన θ = 2nπ ± \(\frac{\pi}{6}\), n ∈ Z

(vi) 1 + sin 2x = (sin 3x – cos 3x)²
Solution:
1 + sin 2x = (sin 3x – cos 3x)²
⇒ 1 + sin 2x = sin²3x + cos²3x – 2 sin 3x cos 3x
⇒ 1 + sin 2x = 1 – sin(2 × 3x)
⇒ sin 6x + sin 2x = 0
⇒ \(2 \sin \left(\frac{6 x+2 x}{2}\right) \cdot \cos \left(\frac{6 x-2 x}{2}\right)=0\)
⇒ sin (4x) . cos 2x = 0
⇒ cos 2x = 0 (లేదా) sin 4x = 0
cos 2x = 0 = cos \(\frac{\pi}{2}\)
ప్రధాన సాధన (2x) = \(\frac{\pi}{2}\)
సార్వత్రిక సాధన 2x = (2n + 1) \(\frac{\pi}{2}\), n ∈ Z
x = \(\frac{n \pi}{2}+\frac{\pi}{4}\), n ∈ Z
sin 4x = 0 = sin(nπ), n ∈ Z
సార్వత్రిక సాధన 4x = nπ, n ∈ Z
4x = nπ
⇒ x = \(\frac{n \pi}{4}\), n ∈ Z
సార్వత్రిక సాధనలు
∴ x = \(\frac{n \pi}{4} ; \frac{n \pi}{2}+\frac{\pi}{4}\), n ∈ Z

(vii) 2 sin²x + sin²2x = 2
Solution:
2 sin²x + sin²(2x) = 2
⇒ 2 sin²x + (2 sin x cos x)² – 2 = 0
⇒ sin²x + 2 sin²x cos²x – 1 = 0
⇒ 2 sin²x cos²x – (1 – sin²x) = 0
⇒ 2 sin²x cos²x – cos²x = 0
⇒ cos²x (2 sin²x – 1) = 0
⇒ cos x = 0 (లేదా) sin²x = \(\frac{1}{2}\)
cos x = 0 = cos \(\frac{\pi}{2}\)
ప్రధాన సాధన
⇒ x = \(\frac{\pi}{2}\)

Question 2.
కింది సమీకరణాలను సాధించండి.
(i) √3 sin θ – cos θ = √2
Solution:

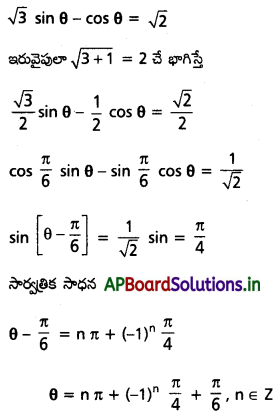
(ii) cot x + cosec x = √3
Solution:

(iii) sin x + √3 cos x = √2
Solution:

Question 3.
కింద సమీకరణాలను సాధించండి.
(i) tan θ + sec θ = √3, 0 ≤ θ ≤ 2π
Solution:

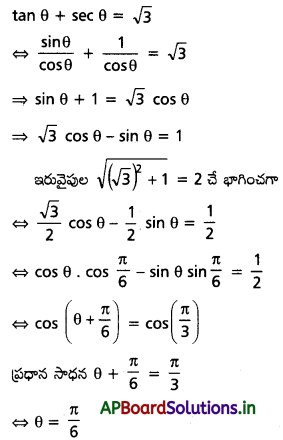
(ii) cos 3x + cos 2x = \(\sin \frac{3 x}{2}+\sin \frac{x}{2}\), 0 ≤ x ≤ 2π
Solution:

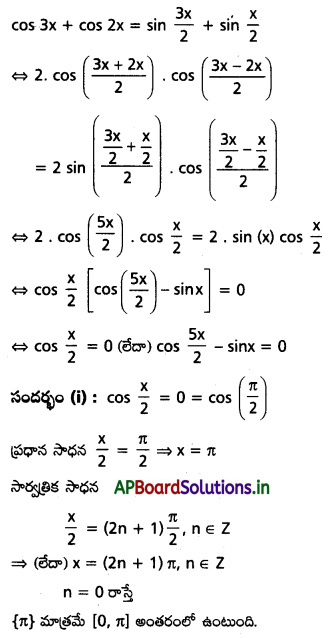
(iii) cot²x – (√3 + 1) cot x + √3 = 0, (0 < x < \(\frac{\pi}{2}\)). [Mar. ’14, ’12]
Solution:
cot²x – (√3 + 1) cot x + √3 = 0
⇒ cot²x – √3 cot x – cot x + √3 = 0
⇒ cot x (cot x – √3) – 1(cot x – √3) = 0
⇒ cot x = √3 (లేదా) cot x = 1
సందర్భం (i): cot x = 1
⇒ tan x = 1
∴ x = \(\left\{\frac{\pi}{4}\right\}\)
సందర్భం (ii): cot x = √3
⇒ tan x = \(\frac{1}{\sqrt{3}}\)
∴ x = \(\left\{\frac{\pi}{6}\right\}\)
∴ సాధనలు \(\left\{\frac{\pi}{6}, \frac{\pi}{4}\right\} \in\left(0, \frac{\pi}{2}\right)\)

(iv) sec x cos 5x + 1 = 0; 0 < x < 2π
Solution:

III.

Question 1.
(i) sin x + sin 2x + sin 3x = cos x + cos 2x + cos 3x ను సాధించండి.
Solution:
(sin 3x + sin x) + sin 2x = (cos 3x + cos x) + cos 2x
⇒ \(\text { 2. } \sin \left(\frac{3 x+x}{2}\right) \cdot \cos \left(\frac{3 x-x}{2}\right)\) + sin 2x = \(2 \cos \left(\frac{3 x+x}{2}\right) \cdot \cos \left(\frac{3 x-x}{2}\right)\) + cos 2x
⇒ 2 . sin 2x . cos x + sin 2x = 2 . cos 2x . cos x + cos 2x
⇒ sin 2x (2 cos x + 1) = cos 2x (2 cos x + 1)
⇒ (2 cos x + 1) (sin 2x – cos 2x ) = 0
⇒ cos x = \(\frac{-1}{2}\) (లేదా) sin 2x = cos 2x (i.e.,) tan (2x) = 1

(ii) x + y = \(\frac{2 \pi}{3}\), sin x + sin y = \(\frac{3}{2}\) అయితే, x, y లను కనుక్కోండి.
Solution:
sin x + sin y = \(\frac{3}{2}\)
\(2 \sin \frac{x+y}{2} \cos \left(\frac{x-y}{2}\right)=\frac{3}{2}\)

(iii) sin 3x + sin x + 2 cos x = sin 2x + 2 cos²x అయితే, సార్వత్రిక సాధనను రాయండి.
Solution:
sin 3x + sin x + 2 cos x = sin 2x + 2 cos²x
⇒ 2 . sin(\(\frac{3 x+x}{2}\)) . cos(\(\frac{3 x-x}{2}\)) + 2 cos x = 2 sin x cos x + 2 cos²x
⇒ 2 . sin 2x . cos x + 2 cos x = 2 cos x (sin x + cos x)
⇒ 2 cos x (sin 2x + 1) = 2 cos x (sin x + cos x)
⇒ 2 cos x [sin 2x + 1 – sin x – cos x) = 0
⇒ cos x = 0 (లేదా) sin 2x – sin x + 1 – cos x = 0

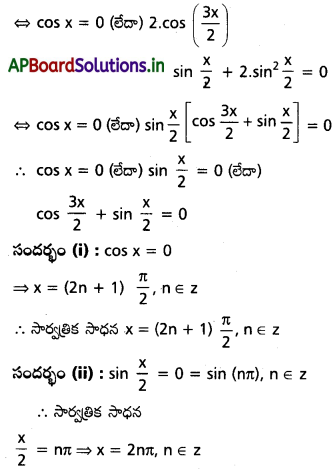
(iv) cos 3x – cos 4x = cos 5x – cos 6x ను సాధించండి.
Solution:
-2 sin 5x . sin x = -2 sin 4x . sin x
⇒ 2 sin x [sin 5x – sin 4x] = 0
⇒ 4 sin x . cos \(\frac{9 x}{2}\) . sin \(\frac{x}{2}\)
(i) sin x = 0
⇒ x = nπ, n ∈ z
(ii) sin \(\frac{x}{2}\) = 0
⇒ \(\frac{x}{2}\) = nπ
⇒ x = 2nπ, n ∈ z
(iii) cos \(\frac{9 x}{2}\) = 0
⇒ \(\frac{9 x}{2}\) = (2n + 1) \(\frac{\pi}{2}\)
⇒ x = (2n + 1) \(\frac{\pi}{9}\), n ∈ z

Question 2.
కింది సమీకరణాలను సాధించండి.
(i) cos 2θ + cos 8θ = cos 5θ
Solution:
cos 2θ + cos 8θ = cos 5θ
⇒ \(2 \cos \left(\frac{2 \theta+8 \theta}{2}\right) \cos \left(\frac{2 \theta-8 \theta}{2}\right)\) – cos 5θ = 0
⇒ 2 cos 5θ . cos 3θ – cos 5θ = 0
⇒ cos 5θ (2 cos 3θ – 1) = 0
If cos 5θ = 0
సాధనలో 5θ = (2n + 1) \(\frac{\pi}{2}\)
θ = (2n + 1) \(\frac{\pi}{10}\), n ∈ z
If 2cos 3θ – 1 = 0
cos 3θ = \(\frac{1}{2}\) = cos \(\frac{\pi}{3}\)
సార్వత్రిక సాధన 3θ = 2nπ ± \(\frac{\pi}{3}\)
θ = \(\frac{2 n \pi}{3} \pm \frac{\pi}{9}\), n ∈ z

(ii) cos θ – cos 7θ = sin 4θ
Solution:
cos θ – cos 7θ = sin 4θ
\(-2 \sin \left(\frac{\theta+7 \theta}{2}\right) \sin \left(\frac{\theta-7 \theta}{2}\right)\) – sin 4θ = 0
⇒ 2 sin 4θ sin 3θ – sin 4θ = 0
⇒ sin 4θ (2 sin 3θ – 1) = 0
If sin 4θ = 0
∴ సార్వత్రిక సాధన 4θ = nπ
θ = \(\frac{n \pi}{4}\), n ∈ z
If 2 sin 3θ – 1 = 0
sin 3θ = \(\frac{1}{2}=\frac{\sin \pi}{6}\)
సార్వత్రిక సాధన 3θ = nπ + (-1)ⁿ \(\frac{\pi}{6}\)
θ = \(\frac{n \pi}{3}+(-1)^n \frac{\pi}{18}\), n ∈ z

(iii) sin θ + sin 5θ = sin 3θ, 0 < θ < π.
Solution:
sin θ + sin 5θ = sin 3θ
sin θ + sin 5θ – sin3θ = 0
sin θ + \(2 \cos \left(\frac{5 \theta+3 \theta}{2}\right) \sin \left(\frac{5 \theta-3 \theta}{2}\right)\) = 0
sin θ + 2 cos 4θ . sin θ = 0
sin θ (1 + 2 cos 4θ) = 0
sin θ = 0, cos 4θ = \(\frac{-1}{2}\)
If sin θ = 0
సార్వత్రిక సాధన θ = nπ, n ∈ Z

Question 3.
(i) (p ≠ -q), tan pθ = cot qθ సమీకరణం సాధనలు, పదాంతరం \(\frac{\pi}{p+q}\) గా కలిగిన అంకశ్రేఢిలో ఉంటాయని చూపండి.
Solution:

(ii) (p ≠ ±q), cos pθ = sin qθ సమీకరణం సాధనలు రెండు అంకశ్రేఢులు అవుతాయని చూపి, వాటి పదాంతరాలను కనుక్కోండి.
Solution:

(iii) (0, π) అంతరంలో tan x + sec x = 2 cos x; cos x ≠ 0 సమీకరణానికి సాధనల సంఖ్యను కనుక్కోండి.
Solution:
tan x + sec x = 2 cos x
\(\frac{\sin x}{\cos x}+\frac{1}{\cos x}\) = 2 cos x
sin x + 1 = 2 cos²x
sin x + 1 = 2(1 – sin²x)
sin x + 1 = (2 – 2 sin²x)
2sin²x + sin x – 1 = 0
2sin²x + 2 sin x – sin x – 1 = 0
2 sin x (sin x + 1) – 1(sin x + 1) = 0
(sin x + 1) (2 sin x – 1) = 0
sin x = -1
∴ sin x = -1
x = \(\frac{-\pi}{2} \text { (or) } \frac{3 \pi}{2}\)
sin x = \(\frac{1}{2}\)
x = \(\frac{\pi}{6} \text { (or) } \frac{5 \pi}{6}\)
(0, π) అంతరంలో, సాధనల సంఖ్య = 2

(iv) α ≠ nπ, n ∈ Z అయితే sin 3α = 4 sin α sin(x + α) sin(x – α) సమీకరణాన్ని సాధించండి.
Solution:
sin 3α = 4 sin α sin(x + α) sin(x – α)
3 sin α – 4 sin³α = 4 sin α (sin²x – sin²α)
sin α తో భాగించగా
3 – 4 sin²α = 4(sin²x – sin²α)
3 – 4 sin²α = 4 sin²x – 4 sin²α
4 sin²x = 3
2 sin²x = \(\frac{3}{2}\)
1 – cos 2x = \(\frac{3}{2}\)
cos 2x = \(\frac{-1}{2}\) = cos \(\frac{2 \pi}{3}\)
2x = 2nπ ± \(\frac{2 \pi}{3}\) ∀ n ∈ Z
x = nπ ± \(\frac{\pi}{3}\), n ∈ Z

Question 4.
(i) tan(π cos θ) = cot(π sin θ) అయితే \(\cos \left(\theta-\frac{\pi}{4}\right)=\pm \frac{1}{2 \sqrt{2}}\) అని చూపండి.
Solution:

(ii) cos θ + sin θ ధనాత్మకం అయ్యేటట్లు θ ఉండే అంతరాన్ని కనుక్కోండి.
Solution:

Question 5.
(i) a cos θ + b sin θ = c, a, b, c ∈ R సమీకరణానికి
α, β లు సాధనలు అయి, a² + b² > 0, cos α ≠ cos β, sin α ≠ sin β అయితే కింది వాటిని ఋజువు చేయండి.
(i) sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
(ii) cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) cos α . cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)
Solution:
a cos θ = b sin θ = c
మొదట దీనిని sin θ లో వర్గ సమీకరణంగా వ్రాస్తే
⇒ a cos θ = c – b sin θ
ఇరువైపులా వర్ణం చేయగా
⇒ a² cos²θ = (c – b sin θ)²
⇒ a² (1 – sin²θ) = c² + b² sin²θ – 2bc sin θ
⇒ (a² + b²) sin²θ – 2bc sin θ + (c² – a²) = 0
ఇది sin θ లో వర్గ సమీకరణం
sin α, sin β లు మూలాలు
(i) మూలాల మొత్తం = sin α + sin β = \(\frac{2 b c}{a^2+b^2}\)
ఇంకా a cos θ + b sin θ = c
దీనిని cos θ లో వర్గ సమీకరణంగా వ్రాస్తే
⇒ b sin θ = c – a cos θ
ఇరువైపులా వర్గం చేయగా
⇒ b² sin²θ = (c – a cos θ)²
⇒ b²(1 – cos²θ) = c² + a² cos²θ – 2 ca cos θ
⇒ (a² + b²) cos²θ – 2 ca cos θ + (c² – b²) = 0
ఇది cos θ లో వర్గ సమీకరణం
cos α, cos β లు మూలాలు
(ii) మూలాల మొత్తం = cos α + cos β = \(\frac{2 a c}{a^2+b^2}\)
(iii) మూలాల లబ్దము = cos α . cos β = \(\frac{c^2-b^2}{a^2+b^2}\)
(iv) మూలాల లబ్దము = sin α . sin β = \(\frac{c^2-a^2}{a^2+b^2}\)

Question 6.
కింది సమీకరణాలకు ఉమ్మడి మూలాలు కనుక్కోండి.
(i) cos 2x + sin 2x = cot x, 2 cos²x + cos²2x = 1
Solution:
tan x = A అనుకుందాం
cos 2x + sin 2x = cot x
⇒ \(\frac{1-\tan ^2 x}{1+\tan ^2 x}+\frac{2 \tan x}{1+\tan ^2 x}=\frac{1}{\tan x}\)
⇒ \(\frac{1-A^2}{1+A^2}+\frac{2 A}{1+A^2}=\frac{1}{A}\)
⇒ (1 – A² + 2A) A = (1 + A²)
⇒ A – A³ + 2A² = 1 + A²
⇒ A³ – A² – A + 1 = 0
⇒ A = 1 పై సమీకరణాన్ని తృప్తిపరుస్తుంది.

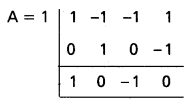
∴ A³ – A² – A + 1 = 0
⇒ (A – 1) (A² – 1) = 0
⇒ (A – 1) (A – 1) (A + 1) = 0
⇒ A = 1, A = -1
⇒ tan x = ±1
⇒ x = (2n + 1)\(\frac{\pi}{4}\), n ∈ z
2 cos²x + cos²2x = 1
⇒ (2 cos²x – 1) + cos²(2x) = 0
⇒ cos 2x + cos²(2x) = 0
⇒ cos 2x (1 + cos 2x) = 0
⇒ cos 2x = 0 (లేదా) cos 2x = -1
సందర్భము (i): cos 2x = 0
⇒ 2x = (2n + 1)\(\frac{\pi}{2}\)
∴ x = (2n + 1)\(\frac{\pi}{4}\), n ∈ z
∴ (2n + 1)\(\frac{\pi}{4}\), n ∈ z ఉమ్మడి మూలం అవుతుంది.

(ii) \(\sqrt{6-\cos x+7 \sin ^2 x}\) + cos x = 0 సమీకరణాన్ని సాధించండి.
Solution:
6 – cos x + 7 sin²x ≥ 0
⇒ 7(1 – cos²x) – cos x + 6 ≥ 0
⇒ 7 – 7 cos²x – cos x + 6 ≥ 0
⇒ 7 cos²x + cos x – 13 ≤ 0
⇒ 7 cos²x + cos x – 13 = 0

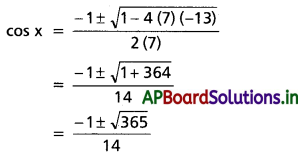
cos x వ్యాప్తి [-1, 1] కాబట్టి దత్త సమీకరణానికి సాధనలేదు.

(iii) |tan x| = tan x + \(\frac{1}{\cos x}\), x ∈ [0, 2π] అయ్యేటట్లు x విలువను కనుక్కోండి.
Solution:
|tan x| = -tan x,
x, 2 లేదా 4వ పాదాలలో ఉంటే
∵ │tan x| = tan x + \(\frac{1}{\cos x}\)
⇒ -tan x = tan x + sec x
⇒ -2 tan x = sec x
⇒ \(-2 \frac{\sin x}{\cos x}-\frac{1}{\cos x}\) = 0
⇒ -2 sin x – 1 = 0
⇒ sin x = \(\frac{-1}{2}=\sin \left(\frac{-\pi}{6}\right)\) = \(\sin \left(2 \pi-\frac{\pi}{6}\right)\)
∴ x = \(\frac{11 \pi}{6}\)