AP Inter 1st Year Maths 1B Important Questions Chapter 2 అక్ష పరివర్తనం

Students get through AP Inter 1st Year Maths 1B Important Questions Chapter 2 అక్ష పరివర్తనం which are most likely to be asked in the exam.

AP Inter 1st Year Maths 1B Important Questions Chapter 2 అక్ష పరివర్తనం

సాధించిన సమస్యలు

ప్రశ్న 1.
అక్షాల సమాంతర పరివర్తన ద్వారా మూల బిందువును (2, 3) కు మారిస్తే బిందువు p నిరూపకాలు (4, −3) గా మారాయి. మూల వ్యవస్థలో (original system) బిందువు P నిరూపకాలు కనుక్కోండి.
సాధన:
(h, k) = (2, 3) + h = 2, k = 3
(x, y) = (4, − 3) ⇒ x = 4, y = -3
x = x + h = 4 + 2 = 6, y = y + k
= -3 + 3 = 0
తొలి నిరూపకాలు (6, 0)

ప్రశ్న 2.
ax² + 2hxy + by² + 2gx + 2fy + c = 0, h² ≠ ab సమీకరణంలో మొదటి తరగతి పదాలు లోపింప చేయడానికి, మూల బిందువును అక్షాలు సమాంతర ‘పరివర్తన ద్వారా ఏ బిందువుకు మార్చాలో కనుక్కోండి.
సాధన:
సమాంతర అక్ష పరివర్తనలో మూల బిందువును (α, β) కు
మార్చితే X = x’ + α
y = y’ + β
దత్త సమీకరణములో ప్రతిక్షేపించగా
a(x’ + α)² + 2h(x’ + α) (y’ + β) + b(y’ + β² + 2g(x’ + α) + 2f(y’ + β) + c = 0
ఇచ్చిన దాని ప్రకారం
ax’² + 2hx’y’ + by’² + 2x’ (aα + hβ + g) + 2y (hα + bβ + f) + aα² + 2hαβ + bβ² + 2gα + 2fβ + c = 0 ……………… (1)
(1) లో మొదటి తరగతి పదాలు లుప్తం కావలెను.
aα + hβ + g = 0 మరియు hα + bβ + f = 0
ఈ సమీకరణాలను α, β ల కొరకు సాధించగా
α = \(\frac{h f-b g}{a b-h^2}\) , β = \(\frac{g h-a f}{a b-h^2}\)
మూల బిందువును మార్చవలసిన బిందువు
\(\left(\frac{h f-b g}{a b-h^2}, \frac{g h-a f}{a b-h^2}\right)\)

ప్రశ్న 3.
ax² + by² + 2gx + 2fy + c = 0, a ≠ 0, b ≠ 0. సమీకరణంలో మొదటి తరగతి పదాలను లోపింప చేయడానికి మూల బిందువును అక్షాల సమాంతర పరివర్తన ద్వారా ఏ బిందువుకు మార్చాలో కనుక్కోండి.
సాధన:
దత్త సమీకరణంలో xy పదముతో సమస్య 2 లో h = 0 రాస్తే
\(\left(\frac{-g}{a}, \frac{-f}{b}\right)\) అనేది కావలసిన బిందువు.

ప్రశ్న 4.
135° కోణంతో అక్షాలను భ్రమణం చేసినప్పుడు P బిందువు (4, -3) గా మారితే మూల వ్యవస్థ దృష్ట్యా P నిరూపకాలు కనుక్కోండి.
సాధన:
ఇక్కడ (x, y) = (4, -3); θ = 135°
(x, y) కు P యొక్క నిరూపకాలు
x = x’ cos θ – y’ sin θ
= 4 cos 135° – (-3) sin 135°
= \(4\left(\frac{-1}{\sqrt{2}}\right)+3\left(\frac{+1}{\sqrt{2}}\right)=\frac{-1}{\sqrt{2}}\)
y = x’ sin θ + y’ cos θ
= 4 sin 135° + (-3) cos 135°
= \(4\left(\frac{1}{\sqrt{2}}\right)-3\left(\frac{-1}{\sqrt{2}}\right)=\frac{7}{\sqrt{2}}\)
తొలి వ్యవస్థలో P నిరూపకాలు \(\left(\frac{-1}{\sqrt{2}}, \frac{7}{\sqrt{2}}\right)\)

ప్రశ్న 5.
a ≠ b అయితే ax² + 2hxy + by² = 0 సమీకరణంలో xy పదం లోపింపచేయడానికి, అక్షాలను భ్రమణ పరివర్తన చేయవలసిన కోణం \(\frac{1}{2}\) Tan^-1 \(\left(\frac{2 h}{a-b}\right)\) అని, a = b అయితే ఈ కోణం \(\frac{\pi}{4}\) అని చూపండి. [Mar. ’13; May ’06]
సాధన:
అక్షాలను θ కోణం భ్రమణం చేస్తే
x =x’ cos θ – y’ sin θ
y = x’ sin θ + y cos θ
దత్త సమీకరణము నూతన రూపము
a(x’ cos θ – y’ sin θ)² +2h(x’ cos θ – y’ sin θ) (x’ sin θ+ y’ cos θ) + b(x’ sin θ + y cos θ)² = 0
x y పదము తొలగించడానికి దాని గుణకము సున్నా చేయుము.
కాబట్టి (b – a) sin θ cos θ + h(cos² θ – sin² θ) = 0
h cos 2θ = \(\frac{a-b}{2}\) sin 2θ
tan 2θ = \(\frac{2h}{a-b}\) , ఐతే a ≠ b
∴ θ = \(\frac{1}{2}\) Tan^-1 \(\left(\frac{2 h}{a-b}\right)\) ఐతే a ≠ b మరియు
θ = \(\frac{\pi}{4}\), ఐతే a = b

ప్రశ్న 6.
మూల బిందువును బిందువు (-2, – 3) కు మార్చి అక్షాలను 45° కోణంతో పరిభ్రమణం చేసినప్పుడు 2x² + 4xy – 5y² + 20x – 22y – 14 = 0 యొక్క రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
(h, k) = (-2, -3), అనుకొంటే h = -2, k = -3
θ = 45°
(x, y) యొక్క నూతన నిరూపకాలు (x, y) అనుకొనుము.
x = x’ cos θ – y’ sin θ + h
= -2 + x’ cos 45° – y’ sin 45°
= -2 + \(\frac{x^{\prime}-y^{\prime}}{\sqrt{2}}\)
y = x’ sin θ + y’ cos θ + k
= x’ sin 45° + y’ cos 45° – 3 = – 3 + \(\frac{x^{\prime}+y^{\prime}}{\sqrt{2}}\)
పరివర్తిత సమీకరణము

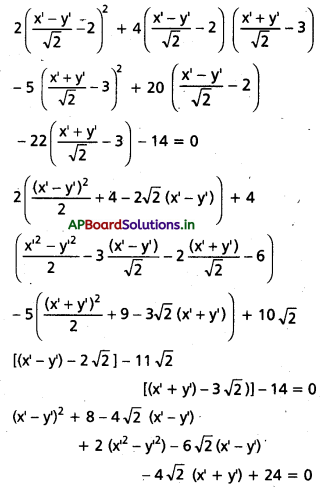
– \(\frac{5}{2}\) (x’ – y’)² – 45 + 15 \(\sqrt{2}\) (x’ + y’) + 10 \(\sqrt{2}\) (x’ – y’) – 40 – 11\(\sqrt{2}\) (x’ + y’) + 66 – 14 = 0
x’² + y’² = 2xy + 2x’² – 2y’² – \(\frac{5}{2}\) (x’² + y’² + 2x’y’) – 1 = 0
\(\frac{1}{2}\)x’² – \(\frac{7}{2}\) y’² – 7x’y’ – 1 = 0
x’² – 7y’² – 14x’y’ – 2 = 0
రూపాంతర సమీకరణము (డాస్లు వదిలి వేయుము)
x² – 7y² – 14xy – 2 = 0

ప్రశ్న 7.
సమాంతర పరివర్తన ద్వారా మూలబిందువును (−2, 3) బిందువుకు మార్చినప్పుడు కొత్త అక్షాల దృష్ట్యా (1, 2) బిందువు నిరూపకాలను కనుక్కోండి.
సాధన:
(h, k) = (-2, 3) సమాంతర పరివర్తన ద్వారా
(x, y) = (1, 2) ను (x’, y’) కి మార్చామని అనుకొనుము.
(x’, y’) = (x – h, y -k) = (1 – (-2), 2 -3) = (3, -1)

ప్రశ్న 8.
అక్షాల సమాంతర పరివర్తన ద్వారా మూల బిందువును (3, 4) కు మార్చినప్పుడు 2x² + 4xy + 5y² = 0 యొక్క రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
(h, k) = (3, 14)
f(x, y) 0, f(x’ + h, y + k) = 0 ప్రకారం దత్త
సమీకరణంలో
x = x’ + 3, y = y’ + 4 లను ప్రతిక్షేపిస్తే
2(x’ + 3)2 + 4(x’ + 3) (y’ + 4) + 5(y’ + 4)² = 0
2x’² + 4x’y’ + 5y’² + 28x’ + 52y’ + 146 = 0
ఈ సమీకరణాన్ని (“గుర్తును తొలగించి)
2x² + 4xy + 5y² + 28x + 52y + 146 = 0.