AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 1 బిందుపథం Exercise 1(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Exercise 1(a)

అభ్యాసం – 1(ఎ)

ప్రశ్న 1.
బిందువు A (4, – 3) నుంచి దూరం 5 గాగల బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A (4, -3) దత్త బిందువు P(x, y) బిందుపథం మీది బిందువు
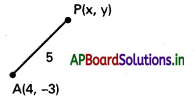
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 1
దత్త నియమము AP = 5
AP² = 25
(x – 4)² + (y + 3)² = 25
x² – 8x + 16 + y² + 6y + 9 − 25 = 0
P యొక్క బిందుపథ సమీకరణము
x² + y² – 8x + 6y = 0

ప్రశ్న 2.
A (-3, 2), B (0, 4) బిందువుల నుంచి సమాన దూరంలో ఉండే బిందు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A (- 3, 2), B (0, 4) లు దత్త బిందువులు
P (x, y) బిందుపథం మీది ఏదేని బిందువు
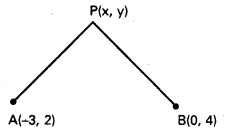
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 2
దత్త నియమము PA = PB
PA² = PB²
(x + 3)² + (y – 2)² = (x – 0)² + (y – 4)²
x² + 6x + 9 + y² – 4y + 4 = x² + y² – 8y + 16
6x + 4y = 3 బిందుపథం మీది సమీకరణము.

ప్రశ్న 3.
మూల బిందువు నుంచి P దూరం, A (1, 2) బిందువు నుంచి P దూరానికి రెట్టింపు అయితే బిందువు P పథ సమీకరణాన్ని కనుక్కోండి. [Mar. ’12]
సాధన:
O (0, 0), A (1, 2) లు దత్త బిందువులు.
P (x, y) బిందుపథం మీది ఏదేని బిందువు.
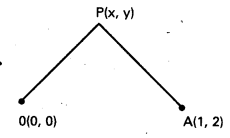
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 3
దత్త నియమము OP = 2AP
OP² = 4 AP²
x² + y² = 4 [(x – 1)² + (y – 2)²]
= 4 (x² – 2x + 1 + y² – 4y+ 4)
x² + y² = 4x² + 4y² – 8x – 16 y + 20
P యొక్క బిందుపథ సమీకరణము
3x² + 3y² – 8x – 16y + 20 = 0

ప్రశ్న 4.
నిరూపకాక్షాల నుంచి సమాన దూరంలో ఉండే బిందువు పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
P(x, y) బిందుపథము మీది ఏదేని బిందువు
PM, PN లు P నుండి X, Y – అక్షాల మీదకు గీయబడిన లంబములు.
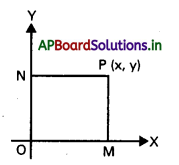
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 4
దత్తాంశం PM = PN ⇒ PM² = PN²
y² = x²
P బిందుపథము x² – y² = 0

ప్రశ్న 5.
A (2, 0) బిందువుకు Y – అక్షానికి సమాన దూరంలో ఉండే. బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A (2, 0) దత్త బిందువు.
P (x, y) బిందుపథం మీది ఏదేని బిందువు
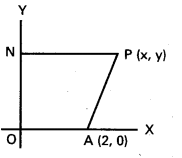
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 5
Y – అక్షానికి లంబంగా PN ను గీయండి.
దత్త నియమము PA = PN
PA² = PN²
(x – 2)² + (y – 0) ² = x²
x² − 4x + 4 + y² = x²
P బిందుపథము y² – 4x + 4 = 0

ప్రశ్న 6.
మూల బిందువు నుంచి P బిందువు దూరానికి వర్గం, P- బిందువు Y– నిరూపకానికి నాలుగురెట్లుంటే బిందువు P – పథ సమీకరణాన్ని కనుక్కోండి. [Mar. 05; June 04]
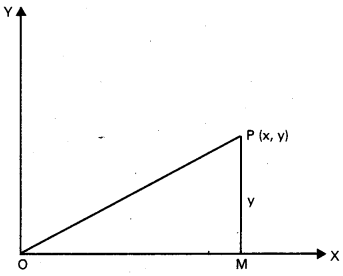
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 6
సాధన:
P(x, y) బిందుపథం మీది ఏదేని బిందువు.
దత్త నియమము OP² = 4y ⇒ x² + y² = 4y
P బిందుపథ సమీకరణము x² + y² – 4y = 0.

ప్రశ్న 7.
A = (a, 0), B = (-a, 0), 0 < |a|< |c|. PA² + PB² = 2c² అయ్యేటట్లు బిందువు P పథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
P (x, y) బిందుపథము మీది ఏదేని బిందువు.
A = (a, 0)
B = (-a, 0)
దత్త నియమము
PA² + PB² = 2c²
(x − a)² + (y − 0)² + (x + a)² + (y − 0)² = 2c²
x² – 2ax + a² + y² + x² + 2ax + a² + y² = 2c²
2x² + 2y² = 2c² – 2a²
∴ x² + y² = c² – a² బిందుపథ సమీకరణము.

II.

ప్రశ్న 1.
(2, 3), (−1, 5) బిందువులను కలిపే రేఖాఖండం, P వద్ద లంబకోణం చేస్తే, P బిందుపథ సమీకరణాన్ని కనుక్కోండి. [Mar. ’13; May ’12; Mar. ’05; June ’04]
సాధన:
A(2, 3), B (−1, 5) లు దత్త బిందువులు.
P(x, y) బిందుపథం మీది ఏదేని బిందువు.
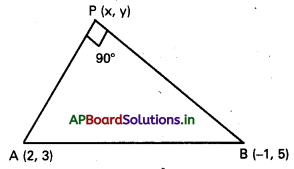
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 7
దత్త నియమము ∠APB = 90°
AP² + PB² = AB²
(x − 2)² + (y − 3)² + (x + 1)² + (y − 5)² = (2 + 1)² + (3 − 5)²
= x² – 4x + 4 + y² – 6y + 9 + x² + 2x + 1 + y² – 10y + 25 = 9 + 4
2x² + 2y² – 2x – 16y + 26 = 0
P యొక్క బిందుపథం x² + y² – x – 8y + 13 = 0
(x, y) ≠ (2, 3) మరియు (x, y) ≠ (-1, 5)

ప్రశ్న 2.
(0, 6), (6, 0) లు కర్ణాగ్రాలుగా గల లంబకోణ త్రిభుజం మూడో శీర్షం బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A(0, 6), B (6, 0) లు కర్ణపు కోణాలు.
P (x, y) మూడవ శీర్షము
∴ దత్త నియమము ∠ APB = 90°
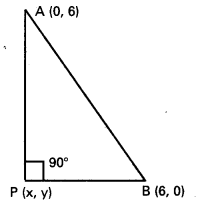
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 8
AP² + PB² = AB²
(x – 0)² + (y – 6)² + (x – 6)² + (y – 0)² = (0 – 6)² + (6 – 0)²
x² + y² -12y + 36 + x² – 12x + 36 + y² = 36 + 36
2x² + 2y² – 12x – 12y = 0
P బిందుపథము x² + y² – 6x – 6y = 0
(x, y) ≠ (0, 6) మరియు (x, y) ≠ (6, 0)

ప్రశ్న 3.
(−5, 0), (5, 0) బిందువుల నుంచి దూరాల భేదం 8గా గల బిందుపథ సమీకరణాన్ని కనుక్కోండి. [May ’11, ’06; Mar. ’04]
సాధన:
A(5, 0), B(-5, 0) లు దత్త బిందువులు.
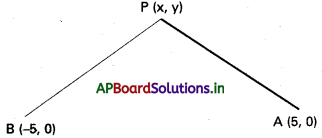
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 9
P(x, y) బిందుపథం మీది ఏదేని బిందువు.
దత్త నియమము |PA – PB| = 8
PA – PB = 8 …………………… (1)
PA² – PB² = [(x – 5)² + (y – 0)²] – [(x + 5)² + (y – o)²]
= x² – 10x + 25+ y² – x² – 10x – 25 – y²
= – 20x
(PA + PB) (PA – PB) = – 20x
(PA + PB) 8 = – 20x
PA + PB = –\(\frac{5}{2}\) x ………………. (2)
(1), (2) లను కూడగా
2PA = –\(\frac{5x}{2}\) + 8 = \(\frac{-5x+16}{2}\)
4PA = – 5x + 16
16PA² = (-5x + 16)²
16 [(x – 5)² + y²] = (- 5x + 16)²
16 [x² – 10x + 25+ y²] = [-5x + 16]²
16x² + 16y² – 160x + 400 = 25x² + 256 – 160 x
9x² – 16y² = 144
144 తో భాగించగా, P బిందుపథం
\(\frac{9 x^2}{144}\) – \(\frac{16 y^2}{144}\) = 1
కనుక \(\frac{x^2}{16}\) – \(\frac{y^2}{9}\) = 1

ప్రశ్న 4.
A = (4, 0), B = (-4, 0), |PA – PB|= 4x P బిందుపథ సమీకరణాన్ని కనుక్కోండి. [May ’13; May ’07]
సాధన:
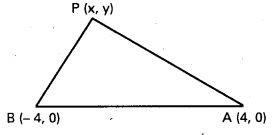
A = (4, 0), B = (- 4, 0) లు దత్త బిందువులు.
P (x, y) బిందుపథం మీది ఏదేని బిందువు.
దత్త నియమము |PA – PB | = 4 ……………… (1)
PA² – PB² = [(x – 4)² + (y – 0)²] – [(x + 4)² + y²]
= x² – 8x + 16 + y² – x² – 8x – 16 – y²
= – 16x
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 10
(PA + PB) (PA – PB) = -16x
(PA + PB) 4 = -16x
PA + PB = – 4x ……………. (2)
(1), (2) లను కూడగా.
2PA = 4 – 4x
PA = 2 – 2x
PA² = (2 – 2x)²
(x – 4)² + (y – 0)² = (2 – 2x)²
x² – 8x + 16 + y² = 4 + 4x² – 8x
3x² – y² = 12
12 తో భాగించగా P యొక్క బిందుపథం \(\frac{3 x^2}{12}-\frac{y^2}{12}\) = 12
\(\frac{x^2}{4}-\frac{y^2}{12}\) = 1

ప్రశ్న 5.
(0, 2), (0, – 2) బిందువుల నుంచి దూరాల మొత్తం 6గా గల బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A (0, 2), B (0, 2) లు దత్త బిందువులు.
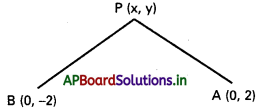
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 11
P(x, y) బిందుపథం మీది ఏదేని బిందువు
దత్త నియమము PA + PB = 6 …………….. (1)
PA² – PB² = [(x – 0)²+(y – 2)²] – [(x – 0)² + (y + 2)²]
= x²+ y² – 4y + 4 – x² – y² – 4y – 4 = -8y
(PA + PB) (PA – PB) = – 8y
6 (PA – PB) = – 8y
PA – PB = – \(\frac{8 y}{6}\)
PA – PB = – \(\frac{4 y}{3}\) ………………. (2)
(1), (2) లను కూడగా 2PA = 6 – \(\frac{4 y}{3}\)
PA = 3 – \(\frac{2 y}{3}\)
PA² = (3 – \(\frac{2 y}{3}\))²
x² + (y – 2)² = (3 – \(\frac{2 y}{3}\))²
x² + y² – 4y + 4 = 9 + \(\frac{4 y^2}{9}\) – 4y
9x² + 9y² + 36 = 81 + 4y²
9x² + 5y² = 45
45 తో భాగించగా
P యొక్క బిందుపథము \(\frac{9 x^2}{45}+\frac{5 y^2}{45}\) = 1
\(\frac{x^2}{5}+\frac{y^2}{9}\) = 1

ప్రశ్న 6.
A = (2, 3), B = (2,-3), PA + PB = 8 అయితే P బిందుపథ సమీకరణాన్ని కనుక్కోండి. [A.P Mar. ’15]
సాధన:
A (2, 3), B (2, -3) లు దత్త బిందువులు.
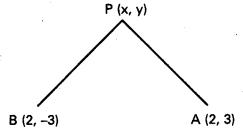
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 12
P(x, y) బిందుపథము మీది ఏదేని బిందువు.
దత్త నియమము PA + PB = 8 ……………. (1)
PA² – PB² = [(x – 2)² + (y – 3)²] – [(x – 2)² + (y + 3)²]
= (x – 2)² + (y – 3)² – (x – 2)² – ( y + 3)²
= (y – 3)² – (y + 3)² = – 12y
(PA + PB) (PA – PB) = – 12y
8 (PA – PB) = -12y
PA – PB = \(\frac{-12 y}{8}\)
PA – PB = \(\frac{-3 y}{2}\) ……………… (2)
(1), (2) లను కూడగా
2PA = 8 – \(\frac{3 y}{2}\) = \(\frac{16-3 y}{2}\)
4PA = 16 – 3y
16PA² = (16 – 3y)²
16 [(x – 2)² + (y – 3)²] = (16 – 3y)²
16(x² – 4x + 4 + y² – 6y + 9) = (16 – 3y)²
16x² + 16y²– 64x – 96y + 208 = 256 + 9y² – 96y
16x² + 7y² – 64x – 48 = 0
P బిందుపథము 16x² + 7y² – 64x – 48 = 0

ప్రశ్న 7.
A(5, 3), B (3, −2) లు రెండు స్థిర బిందువులు. త్రిభుజం PAB వైశాల్యం 9గా ఉండేటట్లు P బిందుపథ సమీకరణాన్ని కనుక్కోండి. [T.S. Mar. ’15, ’06]
సాధన:
A(5, 3), B(3, -2) లు దత్త బిందువులు.
P(x, y) బిందుపథం మీది ఏదేని బిందువు.
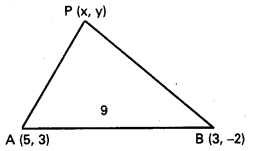
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 13
దత్త నియమము ∆PAB = 9
\(\frac{1}{2}\) |5 (-2 – y) + 3 (y − 3) + x (3 + 2)| = 9
|-10 – 5y + 3y – 9 + 5x| = 18
5x – 2y – 19 = ±18
5x – 2y – 19 = 18 లేదా 5x – 2y – 19 = -18
5x – 2y – 37 = 0 లేదా 5x – 2y – 1 = 0
P యొక్క బిందుపథము (5x – 2y – 37) (5x – 2y – 1) = 0

ప్రశ్న 8.
A(1, 1), B (−2, 3) బిందువులతో 2 వైశాల్యం గా గల త్రిభుజాన్ని ఏర్పరచే బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
A (1, 1), B(-2, 3) లు దత్త బిందువులు
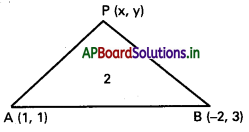
AP Inter 1st Year Maths 1B Solutions Chapter 1 బిందుపథం Ex 1(a) 14
P(x, y) బిందుపథం మీది ఏదేని బిందువు.
దత్త నియమము ∆PAB = 2
\(\frac{1}{2}\) |1 (3) 2 (y – 1) + x (1 – 3)| = 2
|13 – y – 2y + 2 – 2x| = 4
-2x – 3y + 5 = ±4
-2x – 3y + 5 = 45 లేదా – 2x – 3y + 5 = -4
2x + 3y-10 లేదా 2x + 3y – 9 = 0
P బిందుపథము (2x + 3y – 1) (2x + 3y – 9) = 0

ప్రశ్న 9.
(2, 3), (2, – 3) బిందువుల నుంచి P దూరం 2:3 నిష్పత్తిలో ఉంటే, బిందుపథ సమీకరణాన్ని కనుక్కోండి.
సాధన:
P (x, y) బిందుపథం మీది ఏదేని బిందువు
A = (2, 3), B = (2, – 3) లు దత్త బిందువులు.
దత్త నియమము
PA : PB = 2:3
⇒ 3PA = 2PB
⇒ 9PA² = 4PB²
⇒ 9 [(x – 2)² + (y – 3)²] = 4 [(x – 2)² + (y + 3)²]
⇒ 9[x² – 4x + 4 + y² – 6y + 9] = 4 [x² – 4x + 4 + y² + 6y + 9]
∴ 5x² + 5y² – 20 x – 78 y + 65 = 0 బిందుపథ సమీకరణము.

ప్రశ్న 10.
A (1, 2), B (2, -3), C (-2, 3) లు మూడు బిందువులు. PA² + PB² = 2PC² అయ్యేటట్లు P చరిస్తుంది. P బిందుపథ సమీకరణం 7x + 7y + 4 = 0 అని చూపండి. [May ’07]
సాధన:
P (x, y) బిందుపథం మీది ఏదేని బిందువు.
A = (1, 2), B(2, -3), C=(-2, 3) లు దత్త బిందువులు
దత్త నియమము
PA² + PB² = 2 PC²
⇒ (x – 1)² + (y – 2)² + (x – 2)² + (y + 3)² = 2 [(x + 2)² + (y – 3)²].
⇒ 2x² + 2y² – 6x + 2y + 18 = 2x² + 2y² + 8x – 12y + 26
⇒ 14x – 14y + 8 = 0
∴ 7x – 7y + 4 = 0 బిందుపథ సమీకరణం.