AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(b)

అభ్యాసం – 10 (బి)

I.

ప్రశ్న 1.
y = 3x⁴ – 4x వక్రానికి x = 4 వద్ద బిందువు స్పర్శరేఖ వాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = 3x⁴ – 4x
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 12x³ – 4
x = 4 వద్ద స్పర్శరేఖ వాలు = 12 (4)³ – 4
= 12 × 64 – 4
= 768 – 4
= 764

ప్రశ్న 2.
y = \(\frac{x-1}{x-2}\), x ≠ 2 వక్రానికి x = 10 బిందువు వద్ద స్పర్శరేఖ వాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = \(\frac{x-1}{x-2}\)
= \(\frac{x-2+1}{x-2}\)
= 1 + \(\frac{1}{x-2}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 0 + \(\frac{(-1)}{(x-2)^2}\) = –\(\frac{1}{(x-2)^2}\)
x = 10 వద్ద స్పర్శరేఖ వాలు = –\(\frac{1}{(10-2)^2}\)
= –\(\frac{1}{64}\)

ప్రశ్న 3.
y = y³ – x + 1, వక్రానికి x నిరూపకం 2 అయ్యే. బిందువు వద్ద స్పర్శరేఖ వాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = x³ – x + 1
\(\frac{d y}{d x}\) = 3x² – 1
x = 2 వద్ద స్పర్శరేఖ వాలు
3(2)² – 1 = 3 × 4 – 1

ప్రశ్న 4.
y = x³ – 3x + 2 వక్రానికి x నిరూపకం 3 అయ్యే బిందువు వద్ద స్పర్శరేఖ వాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = x³ – 3x + 2
\(\frac{d y}{d x}\) = 3x² – 3
x = 3 స్పర్శరేఖ వాలు = 3(3)² – 3
= 27 – 3 = 24

ప్రశ్న 5.
x = a cos³ θ, y = a sin³ θ వక్రానికి θ = \(\frac{\pi}{4}\) వద్ద అభిలంబరేఖ వాలు కనుక్కోండి.
సాధన:
x = a cos³ θ
\(\frac{\mathrm{dx}}{\mathrm{d} \theta}\) = a(3 cos² θ) (-sin θ)
= -3a cos² θ. sin θ
y = a sin³ θ
\(\frac{\mathrm{dy}}{\mathrm{d} \theta}\) = a (3 sin² θ) cos θ
= 3a sin² θ cos θ

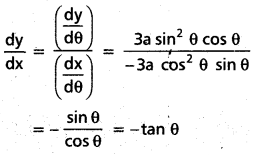
θ = \(\frac{\pi}{4}\), స్పర్శరేఖ వాలు
= -tan \(\frac{\pi}{4}\) = -1
అభిలంబరేఖ వాలు = – \(\frac{1}{m}\) = 1

ప్రశ్న 6.
x = 1 – a sin θ, y = b cos² θ వక్రానికి θ = \(\frac{\pi}{2}\) వద్ద అభిలంబరేఖ వాలు కనుక్కోండి.
సాధన:
x = 1 – a sin θ
\(\frac{d x}{d \theta}\) = – cos θ
y = b cos² θ
\(\frac{d y}{d \theta}\) = b(2 cos θ) (-sin θ) = -2b cos θ sin θ

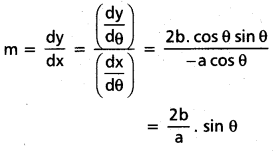
అభిలంబరేఖ వాలు = – \(\frac{1}{m}\) = –\(\frac{a}{2 b \sin \theta}\)
θ = \(\frac{\pi}{2}\) వద్ద, అభిలంబరేఖ వాలు = \(\frac{-a}{2 b \sin \frac{\pi}{2}}\)
= \(\frac{-a}{2 b .1}\)
= \(\frac{-a}{2 b}\)

ప్రశ్న 7.
y = x³ – 3x³ – 9x + 7వక్రం పై ఏ బిందువు వద్ద స్పర్శరేఖలు X-అక్షానికి సమాంతరంగా ఉంటాయో కనుక్కోండి
సాధన:
వక్రం సమీకరణము y = x³ – 3x² – 9x + 7
\(\frac{d y}{d x}\) = 3x² – 6x – 9
స్పర్శరేఖ X – అక్షానికి సమాంతరం
స్పర్శరేఖ వాలు = 0
3x² – 6x – 9 = 0
x² – 2x – 3 = 0
(x – 3)(x + 1) = 0
x = 3 లేదా -1
y = x³ – 3x² – 9x + 7
x = 3y ⇒ 27 – 27 – 27 + 7 = -20
x = -1 ⇒ y = -1 – 3 + 9 + 7 = 12
కావలసిన బిందువులు (3, -20), (-1, 12).

ప్రశ్న 8.
y = (x – 2)² వక్రంపై ఏ బిందువు వద్ద స్పర్శరేఖ (2, 0), (4, 4) బిందువులను కలిపే రేఖకు సమాంతరంగా ఉంటుందో కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = (x – 2)²
\(\frac{d y}{d x}\) = 2(x – 2)
కలిపే జ్యా వాలు A(2, 0), B(4, 4)
= \(\frac{4-0}{4-2}\) = \(\frac{4}{2}\) = 2
స్పర్శరేఖ ఈ జ్యాకి సమాంతరము
2(x – 2) = 2
x – 2 = 1
x = 3
y = (x – 2)² = (3 – 2)² = 1
కావలసిన బిందువు P(3, 1).

ప్రశ్న 9.
y = x³ – 11x + 5 వక్రంపై ఏ బిందువు వద్ద y = x – 11 స్పర్శరేఖ అవుతుందో కనుక్కోండి.
సాధన:
వక్రం సమీకరణం y = x³ – 11x + 5
\(\frac{d y}{d x}\) = 3x² – 11
స్పర్శరేఖ సమీకరణము y = x – 11
స్పర్శరేఖ వాలు = 3x² – 11 = 1
3x² = 12
x² = 4
x = ±2
x = 2 ⇒ y = 2 – 11 = -9
వక్రం మీది బిందువు P.(2, -9).

ప్రశ్న 10.
y = \(\frac{1}{x^2-2 x+3}\) వక్రానికి వాలు ‘0’ అయ్యే ‘ స్పర్శరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణం y = \(\frac{1}{x^2-2 x+3}\)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{-1}{\left(x^2-2 x+3\right)^2}\{2(x-1)\}\)
= \(\frac{-2(x-1)}{\left(x^2-2 x+3\right)^2}\)
స్పర్శరేఖ వాలు = 0
⇒ \(\frac{-2(x \cdot-1)}{\left(x^2-2 x+3\right)^2}\)
x – 1 = 0 ⇒ x = 1
x = 1 వద్ద,
y = \(\frac{1}{x^2-2 x+3}\) = \(\frac{1}{1-2+3}\) = \(\frac{1}{2}\)
P నిరూపకాలు (1, \(\frac{1}{2}\))
స్పర్శరేఖ వాలు = 0
కావలసిన స్పర్శరేఖ సమీకరణము
У – \(\frac{1}{2}\) = 0(x – 1)
2y – 1 = 0

II.

1. కింది వక్రాలకు, ఎదురుగా సూచించిన బిందువుల వద్ద స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.

i) y = x⁴ – 6x³ + 13x² – 10x + 5; (0, 5).
సాధన:
\(\frac{d y}{d x}\) = 4x³ – 18x² + 26x – 10
x = 0 వద్ద,
స్పర్శరేఖ వాలు = 0 − 0 + 0 – 10 = -10
స్పర్శరేఖ సమీకరణము y − 5 = – 10(x – 0)
= -10x
10x + y – 5 = 0
అభిలంబ రేఖ వాలు = –\(\frac{1}{m}\) = \(\frac{1}{10}\)
అభిలంబరేఖ సమీకరణము y − 5 = \(\frac{1}{10}\)(x – 0)
10y – 50 = x ⇒ x – 10y + 50 = 0

ii) y = x³; (1, 1).
సాధన:
\(\frac{d y}{d x}\) = 3x²
\(\frac{d y}{d x}\) = \(\frac{-1}{\left(x^2-2 x+3\right)^2}\{2(x-1)\}\) = \(\frac{-2(x-1)}{\left(x^2-2 x+3\right)^2}\)
స్పర్శరేఖ వాలు =
⇒ \(\frac{-2(x-1)}{\left(x^2-2 x+3\right)^2}\) = 0
x – 1 = 0 ⇒ x = 1
x = 1 వద్ద
y = \(\frac{1}{x^2-2 x+3}\) = \(\frac{1}{1-2+3}\) = \(\frac{1}{2}\)
P నిరూపకాలు(1, \(\frac{1}{2}\))
స్పర్శరేఖ వాలు = 0
కావలసిన స్పర్శ రేఖ సమీకరణ
y – \(\frac{1}{2}\) = 0(x – 1)
2y – 1 = 0

iii) y = x²; (0, 0).
సాధన:
వక్రం సమీకరణము y = x²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = 2x
P(0, 0) వద్ద స్పర్శరేఖ వాలు = 2 – 0 = 0
స్పర్శరేఖ సమీకరణము y – 0 = 0(x – 0)
y = 0
అభిలంబరేఖ స్పర్శరేఖకు లంబంగా ఉంటుంది.
అభిలంబరేఖ సమీకరణము x = k.
అభిలంబరేఖ (0,0) గుండా పోతూ ⇒ k = 0
అభిలంబరేఖ సమీకరణము×= 0.

iv) x = cost, y = sint ; t = \(\frac{\pi}{4}\).
సాధన:

v) y = x² – 4x + 2; (4, 2).
సాధన:
వక్రం సమీకరణ y = x² – 4x + 2
\(\frac{d y}{d x}\) = 2x – 4
P(4, 2) వద్ద, స్పర్శరేఖ వాలు = 2.4 – 4
= 8 – 4 = 4
P వద్ద స్పర్శరేఖ సమీకరణము
y – 2 = 4(x – 4)
= 4x – 16
4x – y – 14 = 0
అభిలంబరేఖ వాలు = – \(\frac{1}{m}\) = –\(\frac{1}{4}\)
P వద్ద అభిలంబరేఖ సమీకరణము
y – 2 = –\(\frac{1}{4}\) (x – 4)
4y – 8 = -x + 4
x + 4y – 12 = 0

vi) y = \(\frac{1}{1+x^2}\); (0, 1).
సాధన:
వక్రం సమీకరణం y = \(\frac{1}{1+x^2}\)
\(\frac{d y}{d x}\) = \(\frac{-2 x}{\left(1+x^2\right)^2}\)
(0, 1) వద్ద, x = 0, స్పర్శరేఖ వాలు = 0
P(0, 1) వద్ద స్పర్శరేఖ సమీకరణము y – 1 = 0(x – 0)
y = 1
అభిలంబరేఖ స్పర్శరేఖకు లంబం.
అభిలంబరేఖ సమీకరణము x = k.
అభిలంబరేఖ P(0, 1) గుండా పోతూ ⇒ 0 = k
P వద్ద అభిలంబరేఖ సమీకరణము x = 0.

ప్రశ్న 2.
xy = 10 వక్రానికి (2, 5) బిందువు వద్ద స్పర్శరేఖ, అభిలంబ రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణం xy = 10.
y = \(\frac{10}{x}\) ; \(\frac{d y}{d x}\) = –\(\frac{10}{x^2}\)
P(2, 5), f'(x₁) = –\(\frac{10}{4}\) = –\(\frac{5}{2}\)
స్పర్శరేఖ సమీకరణము y − y₁ = f(x₁) (x – x₁)
y – 5 = –\(\frac{5}{2}\)(x – 2)
2y – 10 = -5x + 10
5x + 2y – 20 = 0
అభిలంబరేఖ సమీకరణము
y – y₁ = \(-\frac{1}{f^{\prime}\left(x_1\right)}\)(x – x₁)
y – 5 = \(\frac{2}{5}\)(x – 2)
5y – 25 = 2x – 4
i.e., 2x − 5y + 21 = 0

ప్రశ్న 3.
y = x³ + 4x² వక్రానికి (-1, 3) బిందువు వద్ద స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = x³ + 4x²
\(\frac{d y}{d x}\) = 3x² + 8x
P(-1, 3) వద్ద,
స్పర్శరేఖ వాలు = 3(-1)² + 8(-1)
= 3 – 8 = -5
స్పర్శరేఖ సమీకరణము P(-1, 3)
y – y₁ = f'(x₁) (x – x₁)
y – 3 = -5(x + 1) = -5x − 5
5x + y + 2 = 0
P వద్ద అభిలంబరేఖ సమీకరణము
y – y₁ = –\(\frac{1}{f^{\prime}\left(x_1\right)}\) (x – x₁)
y – 3 = \(\frac{1}{5}\)(x + 1)
5y – 15 = x + 1
x – 5y + 16 = 0

ప్రశ్న 4.
x² – 2xy + 4y = 0 వక్రంపై ఒక బిందువు వద్ద స్పర్శరేఖ వాలు –\(\frac{3}{2}\) అయితే, ఆ బిందువు వద్ద స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం. సమీకరణము
x² – 2xy + 4y = 0
x దృష్ట్యా అవకలనం చేయగా
2x – 2x.\(\frac{d y}{d x}\) – 2y + 4. \(\frac{d y}{d x}\) = 0
2(x – y) = 2(x – 2)\(\frac{d y}{d x}\)
\(\frac{d y}{d x}\) = \(\frac{2(x-y)}{2(x-2)}\) = \(\frac{x-y}{x-2}\)
\(\frac{d y}{d x}\) = \(-\frac{3}{2}\)
∴ \(\frac{x-y}{x-2}\) = \(-\frac{3}{2}\)
2x – 2y = -3x + 6
5x – 2y = 6
2y = 5x – 6 —— (2)
P(x, y) బిందువు (1) మీద ఉంది.
x² – x(5x – 6) + 2(5x – 6) = 0
x² – 5x² + 6x + 10x – 12 = 0
-4x² + 16x – 12 = 0
-4(x² – 4x + 3) = 0
x² – 4x + 3 = 0
(x – 1) (x – 3) = 0
x – 1 = 0 లేదా x – 3 = 0
∴ x = 1 లేదా x = 3
సందర్భం (i) : x = 1
(1) లో ప్రతిక్షేపించగా
1 – 2y + 4y = 0
2y = -1 ⇒ y = \(-\frac{1}{2}\)
కావలసిన బిందువు P(1, \(-\frac{1}{2}\))
స్పర్శరేఖ సమీకరణము y + \(\frac{1}{2}\) = –\(\frac{3}{2}\)(x – 1)
\(\frac{2 y+1}{2}\) = \(\frac{-3(x-1)}{2}\)
2y + 1 = -3x + 3
3x + 2y – 2 = 0
అభిలంబరేఖ సమీకరణము
y + \(\frac{1}{2}\) = \(\frac{2}{3}\)(x – 1)
\(\frac{2 y+1}{2}\) = \(\frac{2}{3}\)(x – 1)
6y + 3 = 4x – 4
4x – 6y – 7 = 0
సందర్భ౦ (ii) : x = 3
(1) లో ప్రతిక్షేపించగా, 9 – 6y + 4y = 0
2y = 9⇒ y = \(\frac{9}{2}\)
∴ కావలసిన బిందువు (3, \(\frac{9}{2}\))
స్పర్శరేఖ సమీకరణము y – \(\frac{9}{2}\) = –\(\frac{3}{2}\)(x – 3)
\(\frac{2 y-9}{2}\) = \(\frac{-3(x-3)}{2}\)
2y – 9 = -3x + 9
3x + 2y – 18 = 0
అభిలంబరేఖ సమీకరణము y – \(\frac{9}{2}\) = \(\frac{2}{3}\)(x – 3)
\(\frac{2 y-9}{2}\) = \(\frac{2(x-3)}{3}\)
6y – 27 = 4x – 12
i.e., 4x – 6y + 15 = 0

ప్రశ్న 5.
y = x log x వక్రంపై ఒక బిందువు వద్ద స్పర్శరేఖ వాలు \(\frac{3}{2}\) అయితే, ఆ బిందువు వద్ద స్పర్శరేఖ, అభిలంబ రేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = x log x
\(\frac{d y}{d x}\) = x . \(\frac{1}{x}\) + log x. 1 = 1 + log x.
1 + log x = \(\frac{3}{2}\)
log_e x = \(\frac{1}{2}\) ⇒ x = e^1/2 = \(\sqrt{\mathrm{e}}\)
∴ y = \(\sqrt{\mathrm{e}}\) . log \(\sqrt{\mathrm{e}}\) = \(\frac{\sqrt{\mathrm{e}}}{2}\)
కావలసిన బిందువు P(\(\sqrt{\mathrm{e}}, \frac{\sqrt{\mathrm{e}}}{2}\))

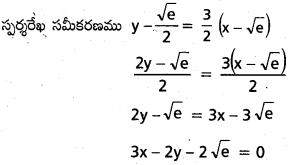
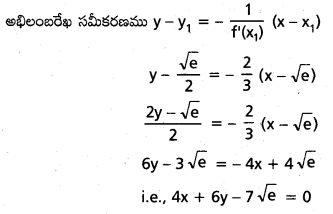
ప్రశ్న 6.
y = 2e^-x/3 వక్రం Y− అక్షాన్ని ఖండించే బిందువు వద్ద ఆ వక్రానికి స్పర్శరేఖ, అభిలంబరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
వక్రం సమీకరణాలు y = 2e^-x/3
Y- అక్షం సమీకరణము x = 0.
y = 2.e° = 2.1 = 2
కావలసిన బిందువు P(0, 2)
\(\frac{d y}{d x}\) = 2\(\left(-\frac{1}{3}\right)\). e^-x/3
ఇప్పుడు x = 0 వద్ద స్పర్శరేఖ వాలు = –\(-\frac{2}{3} \cdot \mathrm{e}^0\)
P వద్ద స్పర్శరేఖ సమీకరణము y – y₁ = f'(x₁)(x – x₁)
y – 2 = –\(\frac{2}{3}\)(x – 0)
3y – 6 = -2x
2x + 3y – 6 = 0
అభిలంబరేఖ సమీకరణం
y – y₁ = \(-\frac{1}{f^{\prime}\left(x_1\right)}\)(x – x₁)
y – 2 = \(\frac{3}{2}\)(x – 0)
2y – 4 = 3x; 3x – 2y + 4 = 0

III.

ప్రశ్న 1.
\(\sqrt{\mathbf{x}}\) + \(\sqrt{\mathbf{y}}\) = \(\sqrt{\mathbf{a}}\) వక్రం పై బిందువు వద్ద స్పర్శ రేఖ సమీకరణం \(y y_1^{-1 / 2}\) + \(x x_1^{-1 / 2}\) = a^1/2 అని చూపండి.
సాధన:
వక్రం సమీకరణము \(\sqrt{x}\) + \(\sqrt{y}\) = \(\sqrt{a}\)
x దృష్ట్యా అవకలనము చేయగా
\(\frac{1}{2 \sqrt{x}}\) + \(\frac{1}{2 \sqrt{y}}\).\(\frac{d y}{d x}\) = 0

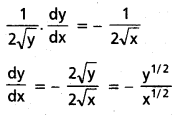
P(x₁, y₁) వద్ద స్పర్శరేఖవాలు = \(-\frac{\left(y_1\right)^{1 / 2}}{\left(x_1\right)^{1 / 2}}\)
P వద్ద స్పర్శరేఖా సమీకరణము

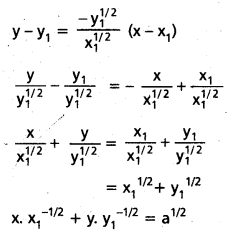
(P వక్రం మీది బిందువు)
P వద్ద స్పర్శరేఖా సమీకరణము
\(y \cdot y_1{ }^{-1 / 2}\) + \(x \cdot x_1^{-1 / 2}\) = a^1/2

ప్రశ్న 2.
x² – y² = 2 వక్రంపై ఏ బిందువుల వద్ద స్పర్శరేఖ వాలు 2కు సమానమవుతోంది ?
సాధన:
స్పర్శరేఖ సమీకరణము x² – y² = 2 ….. (1)
x దృష్ట్యా అవకలనము చేయగా
2x – 2y.\(\frac{d y}{d x}\) = 0
స్పర్శరేఖ వాలు = \(\frac{d y}{d x}\) = 2
∴ 2x – 4y = 0; x = 2y
(1) లో ప్రతిక్షేపించగా, 4y² – y² = 2
3y² = 2
y² = \(\frac{2}{3}\) ⇒ y = ± \(\sqrt{\frac{2}{3}}\)
x = 2y = ±2\(\sqrt{\frac{2}{3}}\)
∴ కావలసిన బిందువు P(\(2 \sqrt{\frac{2}{3}}, \sqrt{\frac{2}{3}}\)) మరియు Q(\(-2 \sqrt{\frac{2}{3}},-\sqrt{\frac{2}{3}}\))

ప్రశ్న 3.
x² + y² = 2, 3x² + y² = 4x వక్రాలకు (1, 1) బిందువు వద్ద ఉమ్మడి స్పర్శరేఖ ఉంటుందని చూపండి.
సాధన:
మొదటి వక్రం సమీకరణము x² + y² = 2
x దృష్ట్యా అవకలనం చేయగా
2x + 2y\(\frac{d y}{d x}\) = 0
2y\(\frac{d y}{d x}\) = -2x
\(\frac{d y}{d x}\) = \(-\frac{2 x}{2 y}\) = \(-\frac{x}{y}\)
P (1, 1) వద్ద స్పర్శరేఖ వాలు = \(\frac{-1}{1}\) = -1
రెండవ వక్రం సమీకరణము 3x² + y² = 4x
x దృష్ట్యా అవకలనము చేయగా
6x + 2y\(\frac{d y}{d x}\) = 4
2y\(\frac{d y}{d x}\) = 4 – 6x
\(\frac{d y}{d x}\) = \(\frac{4-6 x}{2 y}\) = \(\frac{2-3 x}{y}\)
P (1, 1) వద్ద స్పర్శరేఖ వాలు = \(\frac{2-3}{1}\)
= \(-\frac{1}{1}\) = -1
రెండవ వక్రం సమీకరణము P వద్ద స్పర్శరేఖ వాలులు (1, 1) బిందువు గుండా పోతున్నాయి
∴ దత్త వక్రాలకు P (1, 1) వద్ద ఉమ్మడి స్పర్శరేఖ ఉంటుంది.

ప్రశ్న 4.
x³ + y³ = 3axy వక్రంపై (x₁, y₁) బిందువు వద్ద స్పర్శరేఖ సమీకరణం (\(x_1^2\) – ay₁)x + (\(y_1^2\) – ax₁) y = ax₁ y₁ అని చూపండి.
సాధన:
వక్రం సమీకరణము x³ + y³
x దృష్ట్యా అవకలనము చేయగా
3x² + 3y².\(\frac{d y}{d x}\) = 3a(x.\(\frac{d y}{d x}\) + y)
x² + y²\(\frac{d y}{d x}\) = a(x.\(\frac{d y}{d x}\) + y)
= ax.\(\frac{d y}{d x}\) + ay
(y² – ax)\(\frac{d y}{d x}\) = ay – x²
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{a y-x^2}{y^2-a x}\) = \(-\frac{\left(x^2-a y\right)}{\left(y^2-a x\right)}\)
P(x₁, y₁) వద్ద స్పర్శరేఖ వాలు = –\(\frac{\left(x_1^2-a y_1\right)}{\left(y_1^2-a x_1\right)}\)
P వద్ద స్పర్శరేఖ సమీకరణము (x₁, y₁)

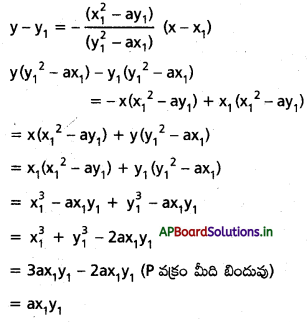
ప్రశ్న 5.
y (1 – x) = x వక్రం పై P (2, −2) బిందువు వద్ద స్పర్శరేఖ నిరూపకాక్షాలపై సమాన పొడవు గల అంతర ఖండాలు చేస్తుందని, ఆ బిందువు వద్ద అభిలంబరేఖ మూల బిందువు ద్వారా పోతుందని చూపండి.
సాధన:
వక్రం సమీకరణము y (1 – x) = x
y = \(\frac{x}{1-x}\)
x దృష్ట్యా అవకలనము చేయగా
\(\frac{d y}{d x}\) = \(\frac{(1-x) \cdot 1-x(-1)}{(1-x)^2}\)
= \(\frac{1-x+x}{(1-x)^2}\) = \(\frac{1}{(1-x)^2}\)
P(2, -2) వద్ద, f'(x₁) = \(\frac{1}{(1-2)^2}\) = 1 = m
P వద్ద స్పర్శరేఖ సమీకరణము
y + 2 = 1(x – 2) = x – 2 ; x – y = 4
\(\frac{x}{4}\) – \(\frac{y}{4}\) = 1 ⇒ \(\frac{x}{4}\) + \(\frac{y}{(-4)}\) = 1
∴ a = 4, b = -4
∴ స్పర్శరేఖ నిరూపకాక్షాల మీద సమానమైన గుర్తులు గల ఇతర ఖండాలు అభిలంబ రేఖా సమీకరణము.
y – y₁ = \(\frac{1}{f^{\prime}\left(x_1\right)}\)(x – x₁)
y + 2 = -(x – 2) = -x + 2
x + y = 0
సమీకరణంలో స్థిరపదం లేదు.
∴ P(2, -2) వద్ద అభిలంబరేఖ మూల బిందువు గుండా పోతుంది.

ప్రశ్న 6.
x^2/3 + y^2/3 = a^2/3 వక్రంపై ఏదైనా బిందువు వద్ద స్పర్శరేఖ నిరూపకాక్షాలను A, B బిందువులలో ఖండిస్తే, AB పొడవు స్థిరమని చూపండి. (Mar. ’14, ’13, ’08, ’07, ’05) (T.S Mar. ’15)

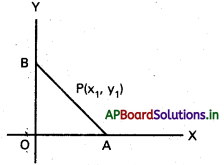
సాధన:
వక్రం సమీకరణం x^2/3 + y^2/3 = a^2/3
x దృష్ట్యా అవకలనం చేయగా

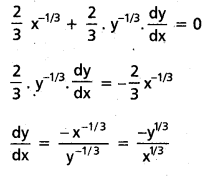
P(x₁, y₁) వద్ద స్పర్శరేఖ సమీకరణము

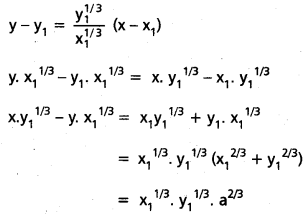
ప్రశ్న 7.
x^myⁿ = a^m+n (mn ≠ 0) వక్రంపై ఏదైనా బిందువు P వద్ద స్పర్శరేఖ నిరూపకాక్షాలను A, B బిందువులలో ఖండిస్తే, AP : PB స్థిరమని చూపండి.

సాధన:
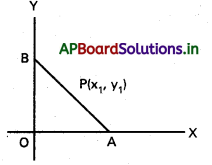
వక్రం సమీకరణం xⁿ. yⁿ = a^m+n
x దృష్ట్యా అవకలనము చేయగా

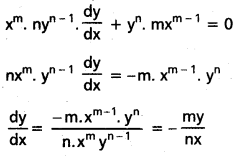
P(x₁, y₁) వద్ద స్పర్శరేఖ వాలు = –\(\frac{m y_1}{n x_1}\)
P వద్ద స్పర్శరేఖ సమీకరణము


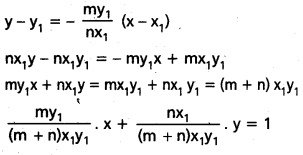
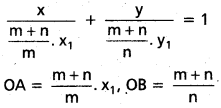
A నిరూపకాలు \(\left[\frac{m+n}{m}, x_1, 0\right]\) మరియు
B నిరూపకాలు \(\left[0, \frac{m+n}{n}, y_1\right]\)
P బిందువు AB ని k : l నిష్పత్తిలో విభజిస్తుంది.

∴P బిందువు AB ని n : m నిష్పత్తిలో విభజిస్తుంది.
i.e., AP : PB = n : m = స్థిరము.