AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(c) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(c)

అభ్యాసం – 10 (సి)

I.

ప్రశ్న 1.
y = b sin \(\frac{x}{a}\) వక్రంపై ఏదైనా బిందువు వద్ద ఉపస్పర్శ ఖండం, ఉపలంబ ఖండాలను కనుక్కోండి.
సాధన:
వక్రం సమీకరణము y = b. sin \(\frac{x}{a}\)
\(\frac{d y}{d x}\) = b.cos \(\frac{x}{a} \cdot \frac{1}{a}\) = \(\frac{b}{a}\). cos \(\frac{x}{a}\)

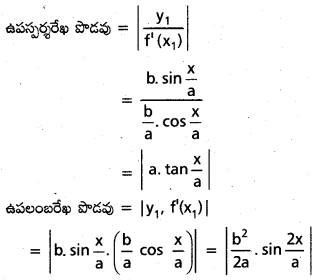
ప్రశ్న 2.
xy = a² అనే వక్రానికి ఏదైనా బిందువు వద్ద ఉపలంబ ఖండం ఆ బిందువు y నిరూపకం ఘనానికి అనుపాతంలో ఉంటుందని చూపండి.
సాధన:
వక్రం సమీకరణము xy = a²
y = \(\frac{a^2}{x}\)
\(\frac{d y}{d x}\) = \(\frac{-a^2}{x^2}\)
ఉపలంబ రేఖ పొడవు’= |y₁, .f'(x₁)|

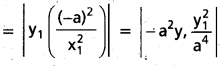
= \(\frac{y_1^3}{a^2}\) ∝ \(y_1^3\) = y నిరూపకం యొక్క ఘనము.

ప్రశ్న 3.
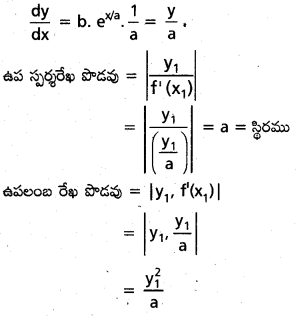
y = be^x/a అనే వక్రంపై ఏదైనా బిందువు (x, y) వద్ద ఉప స్పర్శఖండం స్థిరమనీ, ఉపలంబ ఖండం \(\frac{y^2}{a}\) అని చూపండి.
సాధన:
వక్రం సమీకరణము y = be^x/a
y = a(1 – cos t)

II.

ప్రశ్న 1.
x y^k = a^{k + 1} వక్రంపై ఏ బిందువు వద్ద నైనా ఉపలంబ ఖండం స్థిరం కావాలంటే k విలువ కనుక్కోండి ?
సాధన:
వక్రం సమీకరణము x.y^k = a^{k + 1}
x దృష్ట్యా అవకలనము చేయగా

ఉపలంబ రేఖ పొడవు x, y నిరూపకాల మీద ఆధారపడి మరియు \(\frac{y_1^{k+2}}{k \cdot a^{k+1}}\) విలువ x₁, y₁ ల మీద ఆధారపడి లేదు.
⇒ k + 2 = 0 ⇒ k = – 2

ప్రశ్న 2.
x = a (t + sin t), y = a (1 – cos t) వక్రంపై ఏదైనా బిందువు t వద్ద స్పర్శరేఖ పొడవు, “అభిలంబరేఖ పొడవు, ఉపస్పర్శ ఖండం, ఉపలంబ ఖండాలను కనుక్కోండి. (June ’04)
సాధన:
వక్రం సమీకరణం x = a (t + sin t),
y = a (1 – cost)

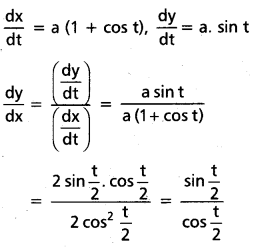
ప్రశ్న 3.
y = \(\frac{a}{2}\) (e^x/a + e^-x/a) వక్రానికి ఏదైనా బిందువు వద్ద అఖిలంబ రేఖ పొడవు, ఉపలంబ ఖండాలను కనుక్కోండి. (Mar. ’13)
సాధన:
వక్రం సమీకరణము y = \(\frac{a}{2}\)(e^x/a + e^-x/a)
= a. cosh \(\left(\frac{x}{a}\right)\)

ప్రశ్న 4.
x = a(cos t + t sin t), y = a(sin t – t cos t) వక్రంపై ఏ బిందువు t వద్ద ఉపస్పర్శ రేఖ, ఉపలంబ ఖండాలను కనుక్కోండి.
సాధన:
వక్రం సమీకరణాలు x = a(cos t + t sin t)

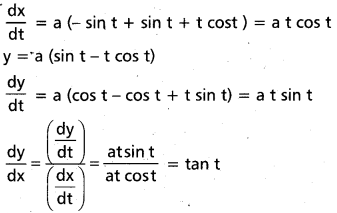
ఉపస్పర్శరేఖ పొడవు = |\(\frac{y_1}{f^{\prime}\left(x_1\right)}\)| = |\(\frac{a(\sin t-t \cos t)}{\tan t}\)|
= |a cot t (sin t – t cos t)|
ఉపలంభరేఖ పొడవు = |y₁. f'(x₁)|
= |a(sin t – t cos t) tan t|
= |a tan t(sin t – t cos t)|