AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Ex 3(d)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 3 సరళరేఖ Exercise 3(d) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 3 సరళరేఖ Exercise 3(d)

అభ్యాసం – 3 (డి)

I. కింది సరళరేఖల మధ్య లఘుకోణాన్ని కనుక్కోండి.

ప్రశ్న 1.
y = 4 – 2x, y = 3x + 7
సాధన:
y = 4 – 2x ⇒ 2x + y − 4 = 0
3x – y + 7 = 0

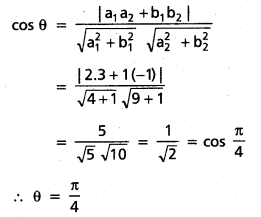
ప్రశ్న 2.
3x + 5y = 7, 2x – y + 4 = 0
సాధన:
cos θ = \(\frac{|6-5|}{\sqrt{9+25} \sqrt{4+1}}=\frac{1}{\sqrt{170}}\)
⇒ θ = cos^-1 \(\left(\frac{1}{\sqrt{170}}\right)\)

ప్రశ్న 3.
y = –\(\sqrt{3}\)x + 5, y = \(\frac{1}{\sqrt{3}}\)x – \(\frac{2}{\sqrt{3}}\)
సాధన:
m₁ = –\(\sqrt{3}\), m₂ = \(\frac{1}{\sqrt{3}}\)
m₁m₂ = (-\(\sqrt{3}\)) /\(\frac{1}{\sqrt{3}}\) = -1
θ = \(\frac{\pi}{2}\) రేఖలు లంబంగా ఉన్నాయి.

ప్రశ్న 4.
ax + by = a + b, a(x − y) + b(x + y) = 2b
సాధన:
ax + by = a + b, (a + b) x + ( a + b) y = 2b

కింది సరళరేఖల మీదికి ఎదురుగా ఇచ్చిన బిందువు నుంచి లంబదూరాన్ని కనుక్కోండి.

ప్రశ్న 5.
5x – 2y + 4 = 0, (−2, −3)
సాధన:
లంబ దూరము
= \(\frac{\left|a x_1+b y_1+c\right|}{\sqrt{a^2+b^2}}\)
= \(\frac{|5(-2)-2(-3)+4|}{\sqrt{25+4}}=\frac{|-10+10|}{\sqrt{29}}\) = 0

ప్రశ్న 6.
3x – 4y + 10 = 0, (3, 4)
సాధన:
లంబ దూరము
= \(\frac{|3.3-4.4+10|}{\sqrt{9+16}}=\frac{3}{5}\)

ప్రశ్న 7.
x – 3y – 4 = 0, (0, 0)
సాధన:
లంబ దూరము
= \(\frac{|0-0-4|}{\sqrt{1+9}}=\frac{4}{\sqrt{10}}\)

కింది సమాంతర రేఖల మధ్యదూరాన్ని కనుక్కోండి.

ప్రశ్న 8.
3x – 4y = 12, 3x – 4y = 7
సాధన:
దత్త రేఖలు 3x – 4y – 12 = 0.
3x – 4y – 7 = 0
సమాంతర రేఖల మధ్య దూరము
= \(\frac{\left|c_1-c_2\right|}{\sqrt{a^2+b^2}}=\frac{|-12+7|}{\sqrt{9+16}}=\frac{5}{5}\) = 1

ప్రశ్న 9.
5x – 3y – 4 = 0, 10x – 6y – 9 = 0 [Mar. ’12]
సాధన:
దత్త రేఖల సమీకరణాలు
10x – 6y – 8 – 0
10x – 6y – 9 = 0 గా తీసుకొనవచ్చు.
సమాంతర రేఖల మధ్యదూరం
= \(\frac{|-8+9|}{\sqrt{100+36}}=\frac{1}{2 \sqrt{34}}\)

ప్రశ్న 10.
2x + 3y + 7 = 0 రేఖకు సమాంతరంగా ఉంటూ (5, 4) బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి. [Mar. ’13]
సాధన:
దత్త రేఖ సమీకరణము 2x + 3y + 7 = 0
కావలసిన రేఖ ఈ రేఖకు సమాంతరము.
సమాంతర రేఖ సమీకరణము 2x + 3y = k
ఈ రేఖ p (5, 4) గుండా పోతుంది.
10 + 12 = k ⇒ k = 22
కావలసిన రేఖ సమీకరణము 2x + 3y = 22
2x + 3y – 22 = 0

ప్రశ్న 11.
5x – 3y + 1 = 0 రేఖకు లంబంగా ఉంటూ (4, 3) బిందువు గుండా పోయే సరళరేఖ సమీకరణం కనుక్కోండి. [T.S Mar. ’15]
సాధన:
దత్త రేఖ సమీకరణము 5x – 3y + 1 = 0
ఈ రేఖకు లంబంగా ఉండే రేఖ సమీకరణము
3x + 5y + k = 0
ఈ రేఖ P (4, -3) గుండా పోతుంది.
– 12 – 15 + k = 0 ⇒ k = 3
కావలసిన రేఖ సమీకరణము
3x + 5y + 3 = 0

ప్రశ్న 12.
6x – 10y + 3 = 0, kx – 5y + 8 = 0 సరళరేఖలు సమాంతరంగా ఉంటే k విలువ కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
6x – 10y + 3 = 0
kx – 5y + 8 = 0
ఈ రేఖలు సమాంతరాలు.
a₁b₂ = a₂b₁
-30 = -10 k
k = 3

ప్రశ్న 13.
3x + 7y – 1 = 0, 7x – py + 3 = 0 సరళరేఖలు లంబంగా ఉంటే p విలువ కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
3x + 7y – 1 = 0
7x – py + 3 = 0
ఈ రేఖలు లంబంగా ఉన్నాయి.
⇒ a₁a₂ + b₁b₂ = 0
3.7 + 7(- p) = 0
7p = 21 = p = 3

ప్రశ్న 14.
y – 3kx + 4 = 0, (2k – 1)x – (8k – 1)y – 6 = 0 సరళరేఖలు లంబంగా ఉంటే k విలువ కనుక్కోండి.
సాధన:
దత్త రేఖల సమీకరణాలు
-3kx + y + 4 =0
(2k – 1)x – (8k – 1)y – 6 = 0
ఈ రేఖలు లంబంగా ఉన్నాయి.
-3k(2k – 1) – 1(8k – 1) = 0
– 6k² + 3k – 8k + 1 = 0
6k² + 5k – 1 = 0
(k + 1) (6k – 1) = 0
k = -1 లేదా 1/6

ప్రశ్న 15.
ఒక చతురస్రం ఒక శీర్షం (-4, 5), దాని వికర్ణం 7x y + 8 = 0 అయితే రెండో వికర్ణం సమీకరణం కనుక్కోండి.

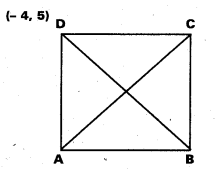
సాధన:
ABCD చతురస్ర వికర్ణం AC సమీకరణము
7x – y + 8 = 0
రెండో వికర్ణం BD AC కి లంబంగా ఉంది.
BD సమీకరణాన్ని X + 7y + k = 0 గా తీసుకొనవచ్చు.
BDD (- 4, 5) గుండా పోతుంది.
– 4 + 35 + k= 0 ⇒ k = 4 – 35 = -31
BD సమీకరణము x + 7y – 31 = 0

II.

ప్రశ్న 1.
బిందువు (1, 3) గుండా పోతూ (3, -5), (−6, 1) బిందువులను కలిపే రేఖకు i) సమాంతరంగా ii) లంబంగా ఉండే సరళరేఖల సమీకరణాలను కనుక్కోండి.

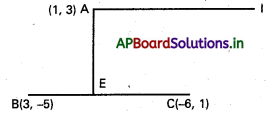
సాధన:
A (3, -5), B(-6, 1) లు దత్త బిందువులు.
AB వాలు = \(\frac{-5-1}{3+6}=\frac{-6}{9}=\frac{-2}{3}\)

i) కావలసిన రేఖ AB కి సమాంతరంగా ఉంటూ (1, 3) గుండా పోతుంది.
కావలసిన రేఖ సమీకరణము
y – 3 = \(\frac{-2}{3}\)(x – 1)
3y – 9 = -2x + 2
2x + 3y – 11 = 0

ii) AE రేఖ AD కి లంబంగా ఉంది.
AE సమీకరణము 3x – 2 y + k = 0
A (1, 3) గుండా పోతుంది.
3 – 6 + k = 0 ⇒ k = 6 – 3 = 3
AE సమీకరణము 3x – 2 y + 3 = 0.

ప్రశ్న 2.
\(\frac{x}{a}-\frac{y}{b}\) = 1 రేఖ X – అక్షాన్ని P వద్ద కలుస్తుంది. P గుండా పోతూ, ఈ రేఖకు లంబంగా ఉండే రేఖ సమీకరణం కనుక్కోండి.
సాధన:

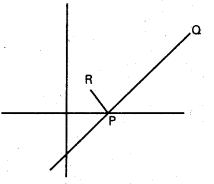
PQ సమీకరణము \(\frac{x}{a}-\frac{y}{b}\) = 1
X – అక్షం సమీకరణము y = 0
\(\frac{x}{a}\) = 1 ⇒ x = a
P నిరూపకాలు (a, 0)
PR రేఖ PQ కి లంబంగా ఉంది.
PR సమీకరణము = \(\frac{x}{b}+\frac{y}{a}\) = k
PR రేఖ P(a, 0) గుండా పోతుంది.
\(\frac{a}{b}\) + 0 = k ⇒ k = a/b
PR. సమీకరణము \(\frac{x}{b}+\frac{y}{a}\) = \(\frac{a}{b}\)

ప్రశ్న 3.
3x + 4y + 6 = 0 రేఖకు లంబంగా ఉంటూ X – అక్షం మీద – 4 అంతర ఖండం చేసే రేఖ సమీకరణం కనుక్కోండి.
సాధన:
దత్తరేఖ సమీకరణము 3x + 4y + 6 = 0
లంబంగా ఉండే రేఖ సమీకరణము
4x – 3y = k
\(\frac{4 x}{k}-\frac{3 y}{k}\) = 1
\(\frac{x}{\left(\frac{k}{4}\right)}+\frac{y}{\left(-\frac{k}{3}\right)}\) = 1
X- అంతరఖండం = \(\frac{k}{4}\) – 4 ⇒ k = -16
కావలసిన రేఖ సమీకరణము 4x – 3y = -16
⇒ 4x – 3y + 16 = 0

ప్రశ్న 4.
XY-తలంలో ఒక చతురస్రానికి A (-1, 1), B (5, 3) లు ఎదురెదురు శీర్షాలు అయితే ఆ చతురస్రం మరొక వికర్ణం (A, B ల గుండా పోని) సమీకరణం కనుక్కోండి.
సాధన:
A (-1, 1), B (5, 3) లు చతురస్రంలో ఎదుటి శీర్షాలు.
AB వాలు = \(\frac{1-3}{-1-5}=\frac{-2}{-6}=\frac{1}{3}\)

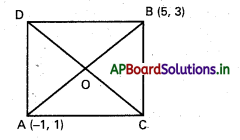
రెండవ వికర్ణము AB కి లంబము.
CD వాలు = – \(\frac{1}{m}\) = -3
‘O’ వికర్ణాల ఖండన బిందువు O
O నిరూపకాలు \(\left(\frac{-1+5}{2}, \frac{1+3}{2}\right)\) = (2, 2)
CD రేఖ O (2, 2) గుండా పోతుంది.
CD సమీకరణము y – 2 = -3 (x – 2)
= -3x + 6
3x + y – 8 = 0

ప్రశ్న 5.
(4, 1) నుంచి 3x 4y + 12 = 0 సరళరేఖకు గీసిన లంబపాదాన్ని కనుక్కోండి.
సాధన:
దత్త రేఖ సమీకరణము 3x – 4y + 12 = 0
(x₁, y₁) నుండి ఈ రేఖ మీదకు లంబపాదం (x₂, y₂) అయితే
ax + by + c = 0, అప్పుడు

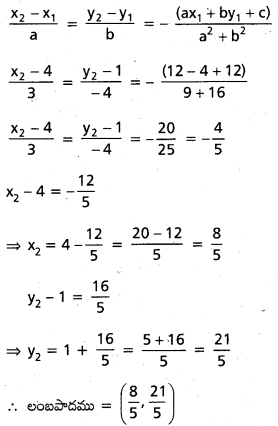
ప్రశ్న 6.
(3, 0) నుంచి 5x + 12y 41 = 0 సరళరేఖకు గీసిన లంబపాదాన్ని కనుక్కోండి.
సాధన:
దత్తరేఖ సమీకరణము 5x + 12y – 41 = 0
(x₂, y₂) నుండి (x₁, y₁) లంబపాదము (x₂, y₂) అయితే
ax + by + c = 0,

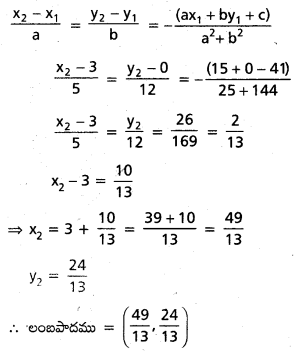
ప్రశ్న 7.
A, B బిందువులను కలిపే రేఖాఖండం లంబసమద్వి ఖండన రేఖ x – 3y – 5 – 0. బిందువు A నిరూపకాలు (−1, −3) అయితే B నిరూపకాలను కనుక్కోండి.
సాధన:

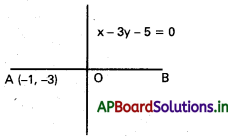
PQ రేఖ AB కి లంబ సమద్విఖండన రేఖ అయితే
PQ దృష్ట్యా A యొక్క ప్రతిబింబము PQ సమీకరణము x – 3y – 5 = 0

A నిరూపకాలు (-1, -3)
ax + by + c = 0 (x₁, y₁) ప్రతిబింబము (x₂, y₂) అయితే

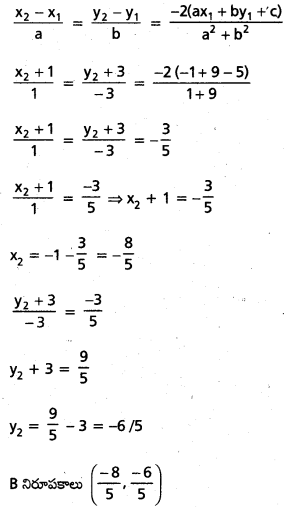
ప్రశ్న 8.
సరళరేఖ 3x + 4y – 1 = 0 లో బిందువు (1, 2) ప్రతిబింబాన్ని కనుక్కోండి.
సాధన:
దత్తరేఖ సమీకరణము 3x + 4y – 1 = 0
(x₁, y₁) దృష్ట్యా ప్రతిబింబము (x₂, y₂) అయితే

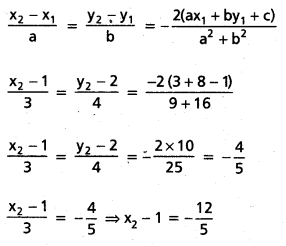
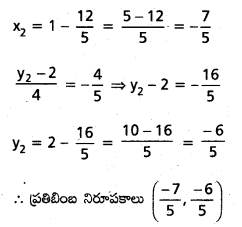
ప్రశ్న 9.
(6, -2) నుండి రేఖ 4x + 3y = 12 కు దూరం, బిందువు (3, 4) నుంచి రేఖ 4x 3y = 12కు దూరంలో సగం ఉంటుందని చూపండి.
సాధన:

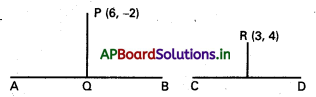
AB సమీకరణము 4x + 3y 12 = 0
PQ = P నుండి లంబపాదము
P = \(\frac{|24-6-12|}{\sqrt{16+9}}=\frac{6}{5}\)
CD సమీకరణము 4x – 3y – 12 = 0
RS = R నుండి లంబదూరము
R = \(\frac{|12-12-12|}{\sqrt{16+9}}=\frac{12}{5}\)
∴ PQ = \(\frac{1}{2}\) RS

ప్రశ్న 10.
స్థిర బిందువు (a, b) గుండాపోయే చల సరళరేఖలకు మూల బిందువు నుంచి లంబపాదాల బిందు పధాన్ని కనుక్కోండి.
సాధన:

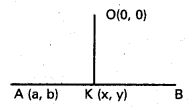
AB రేఖ వాలు m అనుకుందాం.
AB సమీకరణము у – b = m (x – a)
= mx – ma
mx – y + (b – ma) = 0 ………………….. (1)
మూల బిందువు గుండా పోయే AB కి లంబం K నిరూపకాలు (x, y) అనుకుందాం.
AB సమీకరణము x + my = 0 ………………… (2)

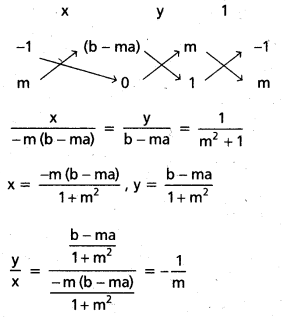
m = -x/y
(1) లో ప్రతిక్షేపించగా
–\(\frac{x^2}{y}\) – y + b + \(\frac{x}{y}\) . a = 0
– x² – y² + by + ax = 0
లేదా x² + y² – ax – by = 0
K బిందు పధము x² + y² – ax – by = 0

III.

ప్రశ్న 1.
x – 7y – 22 = 0, 3x + 4y + 9 = 0, 7x + y – 54 = 0 రేఖలు ఒక సమద్విబాహు సమకోణ త్రిభుజాన్ని ఏర్పరుస్తాయని చూపండి.
సాధన:
దత్త రేఖలు x – 7y – 22 = 0 ……………… (1)
3x + 4y + 9 = 0 ………………… (2)
7x + y – 54 = 0 …………………. (3)

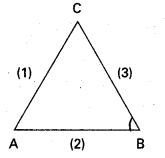
(1), (2) రేఖల మధ్యకోణం ‘A’ అనుకుందాం.

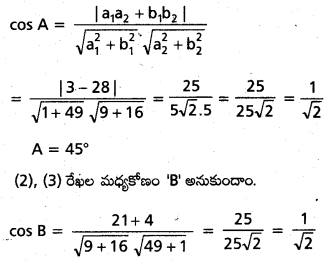
B = 45°
(1), (2) రేఖల మధ్యకోణం ‘A’ అనుకుందాం.
(3), (1) రేఖల మధ్యకోణం ‘C’ అనుకుందాం.
cos C = \(\frac{7-7}{\sqrt{1+49} \sqrt{49+1}}\) = 0 = cos 90°
C = 90°
∠A = ∠B = 45°
∠C = 90°
∴ దత్త రేఖలు లంబకోణ సమద్విబాహు త్రిభుజాన్ని ఏర్పరుస్తున్నాయి.

ప్రశ్న 2.
(-3, 2) బిందువు గుండా పోతూ 3x + y + 4 = 0 రేఖలో 45° కోణాన్ని చేసే రేఖల సమీకరణాలను కనుక్కోండి.
సాధన:
దత్త బిందువు
P(x₁, y₁) = (-3, 2)
దత్త రేఖ 3x – y + 4 = 0 ……………….. (1)
వాలు = m = – \(\frac{a}{b}\) = 3

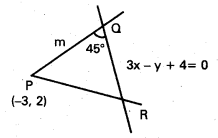
tan 45° = \(\frac{m-3}{1+3 m}\)
\(\left|\frac{m-3}{1+3 m}\right|\) = 1 ⇒ \(\frac{m-3}{1+3 m}\) = 1
m – 3 = 1 + 3m
2m = -4 లేదా 3 m = −2
\(\frac{m-3}{1+3 m}\) = -1 ⇒ m – 3 = -1 – 3m
4m = 2 ⇒ m = 1/2
సందర్భం (i) : m = -2
PQ సమీకరణము
y – 2 = -2(x + 3)
= -2x – 6
2x + y + 4 = 0
సందర్భం (ii) : m = \(\frac{1}{2}\)
PR సమీకరణము
y − 2 = \(\frac{1}{2}\) (x + 3)
2y – 4 = x + 3
x – 2y + 7 = 0

ప్రశ్న 3.
x + y – 4 = 0, 2x+y-6= 0, 5x + 3y – 15 = 0 రేఖలు భుజాలుగా గల త్రిభుజం కోణాలు కనుక్కోండి.
సాధన:
AB సమీకరణము x + y – 4 = 0
BC సమీకరణము 2x + y – 6 = 0
AC సమీకరణము 5x + 3y – 15 = 0

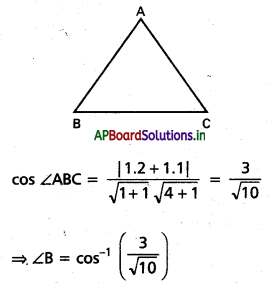
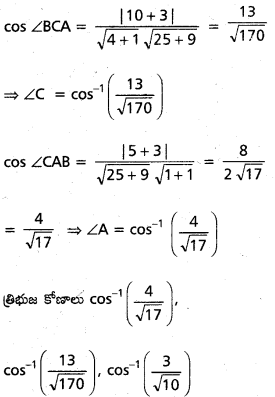
ప్రశ్న 4.
మూల బిందువు x + y = 4, x+5y = 26, 15x – 27y = 424 రేఖల మీదకి గీసిన లంబపాదాలు సరేఖీయాలని చూపండి.
సాధన:
దత్త రేఖలు
x + y – 4 = 0 ………………. (1)
x + 5y – 26 = 0 ……………… (2)
15x – 27y – 424 = 0 ……………… (3)
(x₁, y₁) నుండి (1) మీదకు లంబపాదము (x₂, y₂)
(x₁, y₁) = (0, 0) నుండి (1)
⇒ \(\frac{x_2-0}{1}=\frac{y_2-0}{1}=\frac{-(0+0-4)}{1+1}=\frac{4}{2}\) = 2
⇒ x₂ – 0 = 2, y₂ – 0 = 2
⇒ x₂ = 2, y₂ = 2
∴ P = (2, 2)
(x₁, y₁) నుండి (2) కు లంబపాదము (x₃, y₃)
= (0, 0) నుండి (2).
\(\frac{x_3-0}{1}=\frac{y_3-0}{5}=\frac{-(0+0-26)}{1+25}=\frac{26}{26}\) = 1
x₃ = 1, y₃ = 5 ⇒ Q = (1, 5)
(x₁, y₁) నుండి (3) కు లంబపాదము.
R(x₄, y₄) = (0, 0) నుండి (3)

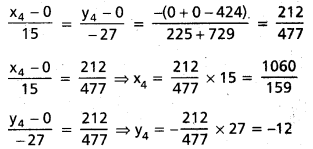
R = (x₄, y₄) = (\(\frac{1060}{159}\), -12)
P,Q రేఖ సమీకరణము
\(\frac{x-2}{1-2}=\frac{y-2}{5-2}\) ⇒ 3x + y – 8 = 0 ………… (4)
(4) లో (x₄, y₄) ను ప్రతిక్షేపించగా,
⇒ (\(\frac{1060}{159}\)) – 12 – 8
= 20 – 20 = 0
∴ మూల బిందువు నుండి లంబ దత్త రేఖలకు గీసిన లంబపాదాలు అనుషక్తాలు.

ప్రశ్న 5.
3x + 2y + 4 = 0, 2x+5y=15 ఖండన బిందువు గుండా పోతూ (2, -1) నుంచి 2 యూనిట్లు దూరంలో గల సరళరేఖల సమీకరణాలు కనుక్కోండి.
సాధన:
L₁ = 3x + 2y + 4 = 0, L₂ = 2x + 5y – 1 = 0
రేఖల ఖండన బిందువు గుండా పోయే రేఖ సమీకరణము
L₁ + 2λ₂ = 0
(3x + 2y +4)+ 2 λ (2x + 5y – 1) = 0
(3 + 2λ) x + (2 + 5λ) y + (4 – λ) = 0 …………… (1)
(2,−1) నుండి (1) కు లంబదూరము = 2
\(\frac{|(3+2 \lambda) 2+(2+5 \lambda)(-1)+(4-\lambda)|}{\sqrt{(3+2 \lambda)^2+(2+5 \lambda)^2}}\) = 2
⇒ \(\frac{|-2 \lambda+8|}{\sqrt{(3+2 \lambda)^2+(2+5 \lambda)^2}}\) = 2
⇒ (−λ + 4)² = 9 + 4λ² + 12λ + 4
⇒ 28λ² + 40λ – 3 = 0
⇒ 28λ² – 2λ + 42λ – 3 = 0
⇒ (2λ + 3) (14λ – 1) = 0
⇒ λ = \(\frac{1}{14}\), λ = –\(\frac{3}{2}\)
λ = \(\frac{1}{14}\) అయితే
కావలసిన రేఖ సమీకరణము 4x + 3y + 5 = 0
λ = –\(\frac{3}{2}\) అయితే
⇒ y – 1 = 0 కావలసిన రేఖ సమీకరణము.

ప్రశ్న 6.
ఒక చతురస్రం ప్రతి భుజం పొడవు 4 యూనిట్లు. ఆ చతురస్ర కేంద్రం(3, 7). దాని ఒక వికర్ణం రేఖ y = x కు సమాంతరంగా ఉంటే, దాని శీర్షాల నిరూపకాలు కనుక్కోండి.
సాధన:
ABCD చతురస్రం వికర్ణాల ఖండన బిందువు దాని కేంద్రం. అవుతుంది. దాని నిరూపకాలు P(3, 7)

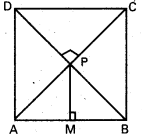
P నుండి AB కి లంబము AB
AB మధ్య బిందువు M.
∴ AM = MB = PM
వికర్ణం y = x కు సమాంతరం కనుక భుజాల నిరూపకాలకు సమానం.
M(3, 5) ⇒ A(1, 5), B(5, 5), C(5, 9), D(1, 9)

ప్రశ్న 7.
ab > 0 అయినప్పుడు ax + by + c = 0 అనే నాలుగు సరళరేఖలతో ఆవృతమైన సమలంబ చతుర్భుజం వైశాల్యం కనుక్కోండి.
సాధన:
AB సమీకరణము ax + by + c = 0 …………….. (1)
CD సమీకరణము ax + by – c = 0 ……………… (2)
BC సమీకరణము ax – by + c = 0 …………….. (3)
AD సమీకరణము ax – by – c = 0 ……………… (4)

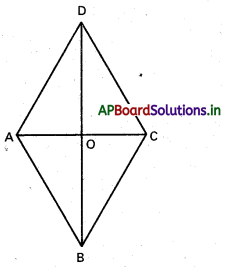
(1), (3) లను సాధిస్తే B నిరూపకాలు \(\left(-\frac{c}{a}, 0\right)\)
(1), (4) సాధిస్తే A నిరూపకాలు \(\left(0,-\frac{c}{b}\right)\)
(2), (3) సాధిస్తే నిరూపకాలు \(\left(0, \frac{c}{b}\right)\)
(2), (4) లను సాధిస్తే D నిరూపకాలు \(\left(\frac{c}{a}, 0\right)\)
ABCD సమ చతుర్భుజ వైశాల్యం = \(\frac{1}{2}\) |Σx₁ (y₂ – y₄) |
= \(\frac{1}{2}\) |0(0 – 0) – \(\frac{c}{a}\left(\frac{c}{b}+\frac{c}{b}\right)\) + 0 (0 – 0) + \(\frac{-c}{a}\left(\frac{c}{b}+\frac{-c}{b}\right)\) |
= \(\frac{1}{2} \cdot \frac{4 c^2}{a b}=\frac{2 c^2}{a b}\) చ॥ యూనిట్లు.

ప్రశ్న 8.
3x + 4y + 5 = 0, 3x + 4y – 2 = 0, 2x + 3y + 1 = 0, 2x + 3y – 7 = 0 సరళరేఖలు భుజాలుగా గల సమాంతర చతుర్భుజ వైశాల్యాన్ని కనుక్కోండి.
సాధన:
దత్త భుజాలు
3x + 4y + 5 = 0 ……………… (1)
3x + 4y – 2 = 0 ………………… (2)
2x + 3y + 1 = 0 …………………. (3)
2x + 3y – 7 = 0 ……………….. (4)

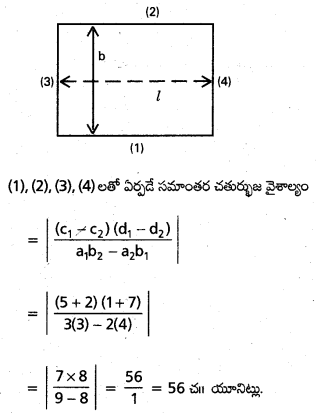
ప్రశ్న 9.
2x + 3y + 4 = 0, 3x + 4y – 5 5 = 0 లతో సూచించిన రెండు రుజు మార్గంలో ఉండే దారులు కూడలి వద్ద ఒక వ్యక్తి నిలబడ్డాడు. అక్కడి నుంచి 6x – 7y + 8 = 0 తో సూచించిన దారికి కనిష్ఠ సమయంలో చేరాలని అనుకున్నాడు. కూడలి నుంచి ఏదారి వెంబడి నడిస్తే కనిష్ఠ సమయంలో 6x – 7y + 8 = 0 నిర్దేశించే దారిని చేరుతాదో ఆ దారిని సూచించే సరళరేఖ సమీకరణాన్ని కనుక్కోండి.
సాధన:
2x + 3y + 4 = 0
3x + 4y – 5 = 0

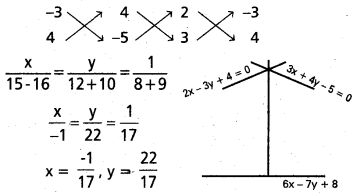
ఇచ్చిన సరళరేఖ 6x – 7y + 8 = 0
సరళరేఖ సమీకరణం 7x + 6y + k = 0 …………. (1)
Eq(1) pass high \(\)
7\(\left(\frac{-1}{17}\right)\) + 6\(\left(\frac{22}{17}\right)\) + k = 0
-7 + 132 + 17k = 0
17k = -125
k = \(\frac{-125}{17}\)
From (1) 7x + 6y – \(\frac{125}{17}\) = 0
119x + 102y – 125 = 0

ప్రశ్న 10.
ఒక కాంతి కిరణం (1,2) బిందువు గుండాపోతూ X – అక్షాన్ని A బిందువు వద్ద తాకి అక్కడ నుంచి పరావర్తనం. చెందిన కిరణం (5,3) బిందువుగుండా పోతే A నిరూపకాలు కనుక్కోండి.
సాధన:
(1, 2) బిందువు గుండాపోయే సమీకరణం యొక్క వాలు ‘m’ అనుకోండి.
y – 2 = m(x – 1)
\(\frac{y-2}{x-1}\) = m

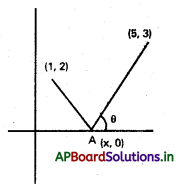
(5,3) బిందువు గుండా
పోయే సమీకరణం వాలు – m అనుకోండి
y – 3 = -m(x – 5)
\(\frac{y-3}{5-x}\) = m
\(\frac{y-2}{x-1}=\frac{y-3}{5-x}\)
A నిరూపకము X అక్షంపై ఉన్నది కనుక y = 0.
\(\frac{-2}{x-1}=\frac{-3}{5-x}\)
10 – 2x = 3x – 3
13 = 5x
x = \(\frac{13}{5}\)
∴ A = \(\left(\frac{13}{5}, 0\right)\)