Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(e) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(e)
అభ్యాసం – 10 (ఇ)
I.
ప్రశ్న 1.
సరళరేఖపై చలించే ఒక కణం t సమయంలో చలించే దూరం’ s = -4t2 + 2t. t = 2 సెకన్లు, t = 8 సెకన్లల మధ్య సరాసరి వేగాన్ని కనుక్కోండి.
సాధన:
s = -4t2 + 2t
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = -8t + 2
వేగం t = 2 వద్ద V = \(\left(\frac{\mathrm{ds}}{\mathrm{dt}}\right)_{\mathrm{t}=2}\)
v = -16 + 2 = -14 యూనిట్లు/సెకను
వేగం t = 8 వద్ద v = \(\left(\frac{d s}{d t}\right)_{t=8}\)
v = -64 + 2 = -62
సరాసరి వేగం = \(\frac{-62-14}{2}\) = -38 యూనిట్లు/సెకను
ప్రశ్న 2.
y = x4 అయితే x = 2, x = 4 ల మధ్య y లో సరాసరి మార్పు రేటును కనుక్కోండి.
సాధన:
y = x4 ⇒ \(\frac{d y}{d t}\) = 4x3
\(\left(\frac{d y}{d t}\right)_{x=2}\) = 32
\(\left(\frac{d y}{d t}\right)_{x=4}\) = 256
సరాసరి మార్పురేటు = \(\frac{256+32}{2}\) = 144.
![]()
ప్రశ్న 3.
సరళరేఖలో చలించే కణం కాలం t, దూరం S ల మధ్య సంబంధం s = t3 + 2t + 3. t = 4 సెకన్ల వద్ద ఆ కణ వేగం, త్వరణం కనుక్కోండి.
సాధన:
s = t3 + 2t + 3
\(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 3t2 + 2 , వేగం v = \([latex]\frac{\mathrm{ds}}{\mathrm{dt}}\)[/latex] = 3ť2 + 2
వేగం t వద్ద = 4
⇒ \(\left(\frac{d s}{d t}\right)_{t=4}\) = 48 + 2 = 50 యూనిట్లు/సెకను
v = 3t2 + 2
\(\frac{d v}{d t}\) = 6t ⇒ a = \(\left(\frac{d v}{d t}\right)_{t=4}\) = 24 యూనిట్లు/సికన్’
ప్రశ్న 4.
సరళరేఖలో చలిస్తున్న కణం, కాలం దూరాల మధ్య సంబంధం s = t3 – 9t2 + 24t – 18. దీని వేగం ఎప్పుడు ఎక్కడ నున్న అవుతుందో కనుక్కోండి.
సాధన:
s = t3 – 9t2 + 24t – 18 కనుక
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 3t2 – 18t + 24
v = 0 ⇒ 3 (t2 – 6t + 8) = 0
∴ (t – 2) (t – 4) = 0
∴ t = 2 or 4
వేగము 2 మరియు 4 సెకన్ల తర్వాత సున్నా..
సందర్భం (i) :
t = 2
s = t3 – 9t2 + 24t – 18
= 8 – 36 + 48 – 18 = 56 -54 = 2
సందర్భం (ii) :
t = 4; s = t3 – 9t2 + 24t – 18
= 64 – 144 + 96 – 18
= 160 – 162 = -2
కణం ‘O’ కు ఇరువైపులా 2 యూనిట్లు.
ప్రశ్న 5.
ఒక సరళరేఖలో చలిస్తున్న కణం t కాలంలో పొందిన స్థానభ్రంశం 5 ను s = 45t + 11t2 – t3 గా ఇస్తే, ఆ కణం నిశ్చల స్థితికి రావడానికి పట్టే కాలాన్ని కనుక్కోండి.
సాధన:
s = 45t + 11t2 – t3
v = \(\frac{\mathrm{ds}}{\mathrm{dt}}\) = 45 + 22t – 3t2
కణం నిశ్చలంగా ఉంటే
⇒ v = 0 = 45 + 22t- 3t2 = 0
⇒ 3t2 – 22t – 45 = 0
⇒ 3t2 – 27t + 5t – 45 = 0
⇒ (3t + 5) (t – 9) = 0 ∴ t = 9 లేదా t = –\(\frac{5}{3}\)
∴ t = 9
∴ కణం 9 సెకన్ల తర్వాత నిశ్చలంగా ఉంటుంది.
II.
ప్రశ్న 1.
ఒక ఘనం ఘనపరిమాణం 8 సెం.మీ./సెకను చొప్పున పెరుగుతుంది. ఘనం అంచు 12 సెం.మీ. ఉన్నప్పుడు ఎంత త్వరగా దీని ఉపరితల వైశాల్యం పెరుగుతుందో కనుక్కోండి. (A.P Mar. ’15, ’14)
సాధన:
ఘనం యొక్క అంచు ‘a’ మరియు ఘన పరిమాణం v అనుకొనుము.
v = a3 —- (1)
ఇచ్చినవి \(\frac{d v}{d t}\) = 8 సెం.మీ.3/సెకను
a = 12 cm
ఉపరితల వైశాల్యం S = 6a2

![]()
ప్రశ్న 2.
నిలకడగా ఉన్న నీటిలో రాయిని వదిలితే వృత్తాకార అలలు ఏర్పడతాయి. ఈ అలలు 5 సెం.మీ./సెకను చొప్పున కదులుతున్నాయి. వృత్త వ్యాసార్ధం 8 సెం.మీ. ఉన్నప్పుడు అలల వైశాల్యం పెరిగే రేటు కనుక్కోండి.
సాధన:
వృత్తాకార అలలు యొక్క వ్యాసార్ధం ‘r’ అనుకోండి.
వృత్త వైశాల్యం A = πr2
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = 2π\(\frac{d r}{d t}\)
ఇచ్చినది r = 8, \(\frac{d r}{d t}\) = 5
\(\frac{\mathrm{dA}}{\mathrm{dt}}\) = 2π(8)(5)
= 80π సెం.మీ2/సెకను
ప్రశ్న 3.
ఒక వృత్త వ్యాసార్ధం పెరిగే రేటు 0.7 సెం.మీ/సెకను, అయితే దీని చుట్టు కొలతలో మార్పు రేటు ఎంత ?
సాధన:
\(\frac{d r}{d t}\) = 0.7 సెం.మీ/సెకను
చుట్టుకొలత C = 2πr
\(\frac{\mathrm{dc}}{\mathrm{dt}}\) = 2π\(\frac{\mathrm{dr}}{\mathrm{dt}}\)
= 2π (0.7) = 1.4π సెం.మీ/సెకను.
ప్రశ్న 4.
ఒక బెల్తూన్న గ్యాస్తో నింపుతుంటే అది గోళరూపంలో ఉంటుంది. దీనిని సెకనుకు 900 ఘన సెంటీమీటర్లతో గ్యాసు నింపుతున్నారు. గోళ వ్యాసార్ధం 15 సెం.మీ. ఉన్నప్పుడు వ్యాసార్ధంలో మార్పు రేటును కనుక్కోండి.
సాధన:
\(\frac{d v}{d t}\) = 900 సెం.మీ./సెకను
r = 15 సెం.మీ.
గోళము యొక్క ఘన పరిమాణం v = \(\frac{4}{3} \pi r^3\)

ప్రశ్న 5.
గాలి బుడగ వ్యాసార్ధంలో మార్పురేటు \(\frac{1}{2}\) సెం.మీ./సెకను, గాలి బుడగ వ్యాసార్ధం 1 సెం.మీ. ఉన్నప్పుడు దీని ఘన పరిమాణం ఏ రేటులో పెరుగుతుంది ?
సాధన:
\(\frac{d r}{d t}\) = \(\frac{1}{2}\) సెం.మీ./సెకను
వ్యాసార్ధం r = 1 సెం.మీ.
గోళము యొక్క ఘన పరిమాణం v = \(\frac{4}{3} \pi r^3\)
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = \(4 \pi r^2 \frac{d r}{d t}\)
= 4π(1)2\(\frac{1}{2}\)
= 2π సెం.మీ./సెకన్.
ప్రశ్న 6.
ఒక వస్తువును 980 మీ./సెకను వేగంతో పైకి విసిరామనుకొందాం. దీని స్థానం s = -4.9 t2 + 980 t గా ఉంటుంది. వస్తువు చేరిన గరిష్ట ఎత్తు కనుక్కోండి.
సాధన:
s = -4.9 t2 + 980 t
\(\frac{\mathrm{ds}}{\mathrm{dt}}\) = -9.8 t + 980
v = -9.8 t + 980
గరిష్ఠ ఎత్తు, v = 0
-9.8 t + 980 = 0
980 = 9.8t
\(\frac{980}{9.8}\) = t
100 = t
s = -4.9(100)2 + 980(100)
s = -49000 + 98000
s = 49000 యూనిట్లు.
ప్రశ్న 7.
ఒక రకం బాక్టీరియా t సెకనులలో t(3/2) వృద్ధి చెందుతుంది. t = 4 గంటలకు బాక్టీరియా వృద్ధిరేటు కనుక్కోండి.
సాధన:
t సెకన్ల వద్ద బాక్టీరియా వృద్ధి g అనుకొందాం.
అప్పుడు g(t) = t3/2
t సెకన్ల వద్ద బాక్టీరియా వృద్ధిరేటు
g'(t) = \(\frac{3}{2} t^{1 / 2}\)
ఇచ్చినది t = 4 గం.
g'(t) = \(\frac{3}{2}\) (4 × 60 × 60)1/2
= \(\frac{3}{2}\)(2 × 60) = 180
ప్రశ్న 8.
పొడవు 8 మీ., వెడల్పు 4 మీ., ఎత్తు 3 మీ. గల దీర్ఘ చతుస్రాకారపు చేపల తొట్టి ఉందనుకొందాం. దీనిని 0.4 మీ. 3/సెకను చొప్పున నీటితో నింపుతున్నారను కొందాం. నీటిమట్టం 2.5 మీ. ఉన్నప్పుడు నీటి మట్టం ఎత్తులో మార్పురేటును కనుక్కోండి.
సాధన:
దీర్ఘచతురస్రాకారపు చేపల తొట్టి పొడవు l = 8 మీ.
దీర్ఘచతురస్రాకారపు చేపల తొట్టి వెడల్పు b = 4 మీ.
దీర్ఘచతురస్రాకారపు చేపల తొట్టి ఎత్తు h = 3 మీ.
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 0.4 మీ./సెకన్
v = lbh
= 8(4)(3) = 96
v = lbh
⇒ log v = log l + log b + log h
\(\frac{1}{v} \frac{d v}{d t}\) = \(\frac{1}{h} \frac{d h}{d t}\)
\(\frac{0.4}{96}\) = \(\frac{1}{2.5} \frac{\mathrm{dh}}{\mathrm{dt}}\)
\(\frac{1}{96}\) = \(\frac{\mathrm{dh}}{\mathrm{dt}}\) at h = 2.5
గమనిక: Text book Ans. \(\frac{1}{80}\) will get when h = 3.
ప్రశ్న 9.
ఒక విలోమ శంకువు ఆకారపు పాత్ర ఎత్తు 8 మీ., పై వ్యాసార్ధం 6 మీ. దీనిలో 2 మీ. / నిమిషానికి చొప్పున నీటితో నింపినప్పుడు నీటి మట్టం 4 మీ. ఉన్నప్పుడు నీటి మట్టం పెరిగే రేటు ఎంత ?
(May 2013)
సాధన:
h = 8m = OC
r = 6m = AB
\(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 2 మీ.3/ని.
Δ OAB మరియు OCD
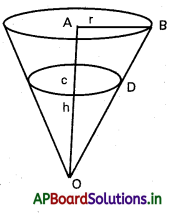
సరూప త్రిభుజాలు
\(\frac{C D}{A B}\) = \(\frac{O C}{O A}\)
\(\frac{r}{6}\) = \(\frac{h}{8}\)
r = h\(\frac{3}{4}\)
శంకువు ఘన పరిమాణం v = \(\frac{1}{3} \pi r^2 h\)

![]()
ప్రశ్న 10.
ఒక వస్తువును C(x) యూనిట్లు ఉత్పత్తి చేయడానికి అయ్యే మొత్తం ఖర్చు C(x) 0.007x3 – 0.003x2 + 15x + 4000. ఆ వస్తువును 17 యూనిట్లు ఉత్పత్తి చేయడానికి ఉపాంత ఖర్చును కనుక్కోండి.
సాధన:
ఉపాంత ఖర్చు m అనుకొందాం. అప్పుడు
M = \(\frac{\mathrm{dc}}{\mathrm{dx}}\)
Hence
M = \(\frac{d}{d x}\)(0.007x3 – 0.003x2 + 15x + 4000)
= (0.007) (3x2) – (0.003) (2x) + 15
(M)x = 17 =
x = 17 వద్ద ఉపాంత ఖర్చు
(M)x = 17 = (0.007) 867 – (0.003)’ (34) + 15
= 6.069 – 0.102 + 15
= 20.967.
ప్రశ్న 11.
x సంఖ్యలో ఒక వస్తువును అమ్మగా వచ్చిన మొత్తం ఆదాయం R(x) = 13x2 + 26x + 15. x = 7 వద్ద ఉపాంత ఆదాయం కనుక్కోండి.
సాధన:
ఉపాంత ఆదాయం m అనుకొందాం. అప్పుడు
m = \(\frac{d R}{d x}\)
ఇక్కడ R(x) = 13x2 + 26x + 15
∴ m = 26x + 26
x = 7 వద్ద ఉపాంత ఆదాయం
(M)x = 7 = 26(7) + 26
= 208.
ప్రశ్న 12.
y = 2x2 పై P అనే బిందువు కదులుతుంది. P యొక్క x నిరూపకం మార్పురేటు సెకనుకు 4 యూనిట్లు బిందువు (2, 8) వద్ద P యొక్క y ని నిరూపకం పెరిగే రేటును కనుక్కోండి.
సాధన:
y = 2x2 కనుక
\(\frac{d y}{d x}\) = 4x. \(\frac{\mathrm{dx}}{\mathrm{dt}}\)
x = 2, అయినప్పుడు \(\frac{\mathrm{dx}}{\mathrm{dt}}\) = 4. \(\frac{\mathrm{dy}}{\mathrm{dt}}\)
= 4(2).4 = 32
y నిరూపకము 32 యూనిట్లు/సెకను రేటుకు పెరుగుతుంది.