AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Ex 3(d)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Chapter 3 మాత్రికలు Exercise 3(d) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1A Solutions Chapter 3 మాత్రికలు Exercise 3(d)

I.

Question 1.
కింది మాత్రికల నిర్ధారకాలు కనుక్కోండి.
(i) \(\left[\begin{array}{cc}
2 & 1 \\
1 & -5
\end{array}\right]\)
Solution:
det A = ad – bc
= 2(-5) – 1(1)
= -10 – 1
= -11

(ii) \(\left[\begin{array}{cc}
4 & 5 \\
-6 & 2
\end{array}\right]\)
Solution:
det A = 4(2) – (-6)(5)
= 8 + 30
= 38

(ii) \(\left[\begin{array}{cc}
\mathbf{i} & 0 \\
0 & -\mathbf{i}
\end{array}\right]\)
Solution:
det A = -i² – 0
= 1 – 0
= 1

(iv) \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\)
Solution:
det A = 0(0 – 1) – 1(0 – 1) + 1(1 – 0)
= 1 + 1
= 2

(v) \(\left[\begin{array}{ccc}
1 & 4 & 2 \\
2 & -1 & 4 \\
-3 & 7 & 6
\end{array}\right]\)
Solution:
det A = 1(-6 – 28) – 4(12 + 12) + 2(14 – 3)
= -34 – 96 + 22
= -108

(vi) \(\left[\begin{array}{ccc}
2 & -1 & 4 \\
4 & -3 & 1 \\
1 & 2 & 1
\end{array}\right]\)
Solution:
det A = 2(-3 – 2) + 1(4 – 1) + 4(8 + 3)
= -10 + 3 + 44
= 37

(vii) \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
4 & -1 & 7 \\
2 & 4 & -6
\end{array}\right]\)
Solution:
det A = 0,
∵ R₁ మరియు R₃ ల అనురూప మూలకాలు సమాన నిష్పత్తిలో ఉన్నవి.

(viii) \(\left[\begin{array}{lll}
\mathbf{a} & \mathbf{h} & \mathbf{g} \\
\mathbf{h} & \mathbf{b} & \mathbf{f} \\
\mathbf{g} & \mathbf{f} & \mathbf{c}
\end{array}\right]\)
Solution:
det A = a(bc – f²) – h(ch – fg) + g(hf – bg)
= abc – af² – ch² + fgh + fgh – bg²
= abc + 2fgh – af² – bg² – ch²

(ix) \(\left[\begin{array}{lll}
\mathbf{a} & \boldsymbol{b} & \mathbf{c} \\
\mathbf{b} & \mathbf{c} & \mathbf{a} \\
\mathbf{c} & \mathbf{a} & \mathbf{b}
\end{array}\right]\)
Solution:
det A = a(bc – a²) – b(b² – ac) + c(ab – c²)
= abc – a³ – b³ + abc + abc – c³
= 3abc – a³ – b³ – c³

(x) \(\left[\begin{array}{ccc}
\mathbf{1}^2 & 2^2 & 3^2 \\
2^2 & 3^2 & 4^2 \\
3^2 & 4^2 & 5^2
\end{array}\right]\)
Solution:
det A = \(\left|\begin{array}{ccc}
1 & 4 & 9 \\
4 & 9 & 16 \\
9 & 16 & 25
\end{array}\right|\)
= 1(225 – 256) – 4(100 – 144) + 9(64 – 81)
= -31 + 176 – 153
= -184 + 176
= -8

Question 2.
A = \(\left[\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right]\) అయి, det A = 45 అయితే x విలువ కనుక్కోండి. [Mar. ’07, ’03]
Solution:
det A = 45
⇒ \(\left|\begin{array}{ccc}
1 & 0 & 0 \\
2 & 3 & 4 \\
5 & -6 & x
\end{array}\right|\) = 45
⇒ 3x + 24 = 45
⇒ 3x – 45 + 24 = 0
⇒ 3x – 21 = 0
⇒ x = 7

II.

Question 1.
\(\left|\begin{array}{lll}
b c & b+c & 1 \\
c a & c+a & 1 \\
a b & a+b & 1
\end{array}\right|\) = (a – b) (b – c) (c – a) అని చూపండి.
Solution:

Question 2.
\(\left|\begin{array}{ccc}
b+c & c+a & a+b \\
a+b & b+c & c+a \\
a & b & c
\end{array}\right|\) = a³ + b³ + c³ – 3abc అని చూపండి. [May ’13, ’07; Mar. ’08]
Solution:

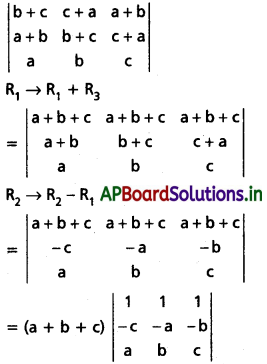
= (a + b + c) [(-ac + b²) – (-c² + ab) + (-bc + a²))
= (a + b + c) (-ac + b² + c² – ab – bc + a²)
= (a + b + c) (a² + b² + c² – ab – bc – ca)
= a³ + b³ + c³ – 3abc

Question 3.
\(\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|\) = 4xyz అని చూపండి.
Solution:
L.H.S. = \(\left|\begin{array}{ccc}
\mathbf{y}+\mathbf{z} & \mathbf{x} & \mathbf{x} \\
\mathbf{y} & \mathbf{z}+\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{z} & \mathbf{x}+\mathbf{y}
\end{array}\right|\)
= (y + z) [(z + x) (x + y) – yz] – x[y(x + y) – yz] + x[yz – z(z + x)]
= (y + z) (zx + yz + x² + xy – yz) – x(xy + y² – yz) + x(yz – z² – zx)
= (y + z) (zx + x² + xy) – x(xy + y² – yz) + x(yz – z² – zx)
= xyz + x²y + xy² + xz² + x²z + xyz – x²y – xy² + xyz + xyz – xz² – x²z
= 4xyz

Question 4.
\(\left|\begin{array}{ccc}
a & a^2 & 1+a^3 \\
b & b^2 & 1+b^3 \\
c & c^2 & 1+c^3
\end{array}\right|\) = 0, \(\left|\begin{array}{lll}
a & a^2 & 1 \\
b & b^2 & 1 \\
c & c^2 & 1
\end{array}\right|\) ≠ 0 అయితే abc = -1 అని చూపండి.
సూచన: ఒక చతురస్ర మాత్రికలో ఏదైనా ఒక అడ్డు వరుస (లేదా నిలువు వరుస) లోని ప్రతీ మూలకం రెండు సంఖ్యల మొత్తంగా ఉంటే, ఆ మాత్రిక నిర్ధారకాన్ని రెండు మాత్రికల నిర్ధారకాలు మొత్తంగా వ్రాయవచ్చు.
Solution:

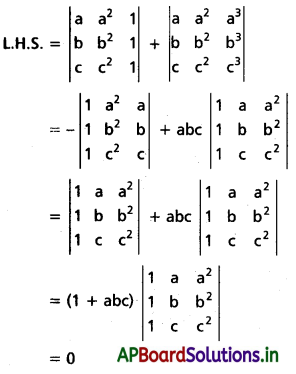
∴ 1 + abc = 0
⇒ abc = -1

Question 5.
నిర్ధారకాన్ని విస్తరించండి.
(i) \(\left|\begin{array}{ccc}
a & a^2 & b c \\
b & b^2 & c a \\
c & c^2 & a b
\end{array}\right|=\left|\begin{array}{ccc}
1 & a^2 & a^3 \\
1 & b^2 & b^3 \\
1 & c^2 & c^3
\end{array}\right|\)
Solution:

(ii) \(\begin{array}{ccc}
a x & b y & c z \\
x^2 & y^2 & z^2 \\
1 & 1 & 1
\end{array}=\left|\begin{array}{ccc}
a & b & c \\
x & y & z \\
y z & z x & x y
\end{array}\right|\)
Solution:

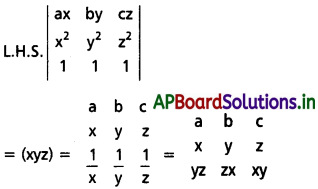
(iii) \(\begin{array}{lll}
1 & b c & b+c \\
1 & c a & c+a \\
1 & a b & a+b
\end{array}=\left|\begin{array}{lll}
1 & a & a^2 \\
1 & b & b^2 \\
1 & c & c^2
\end{array}\right|\) అని నిరూపించండి.
Solution:

Question 6.
Δ₁ = \(\left|\begin{array}{ccc}
a_1^2+b_1+c_1 & a_1 a_2+b_2+c_2 & a_1 a_3+b_3+c_3 \\
b_1 b_2+c_1 & b_2^2+c_2 & b_2 b_3+c_3 \\
c_3 c_1 & c_3 c_2 & c_3^2
\end{array}\right|\) మరియు Δ₂ = \(\left|\begin{array}{lll}
a_1 & b_2 & c_2 \\
a_2 & b_2 & c_2 \\
a_3 & b_3 & c_3
\end{array}\right|\), అయితే \(\frac{\Delta_1}{\Delta_2}\) విలువ కనుక్కోండి.
Solution:

Question 7.
Δ₁ = \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|\), Δ₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\), Δ₁ = Δ₂ అయితే cos²α + cos²β + cos²γ = 1 అని చూపండి.
Solution:
Δ₁ = \(\left|\begin{array}{ccc}
1 & \cos \alpha & \cos \beta \\
\cos \alpha & 1 & \cos \gamma \\
\cos \beta & \cos \alpha & 1
\end{array}\right|\)
= 1(1 – cos²γ) – cos α (cos α – cos β cos γ) + cos β (cos α cos γ – cos β)
= 1 – cos²γ – cos²α + cos α cos β cos γ + cos α cos β cos γ – cos²β
= 1 – cos²γ – cos²α – cos²β + 2 cos α cos β cos γ
Δ₂ = \(\left|\begin{array}{ccc}
0 & \cos \alpha & \cos \beta \\
\cos \alpha & 0 & \cos \gamma \\
\cos \beta & \cos \gamma & 0
\end{array}\right|\)
= 0(0 – cos²γ) – cos α (0 – cos γ cos β) + cos β (cos α cos γ – 0)
= cos α cos β cos γ + cos α cos β cos γ
= 2 cos α cos β cos γ
ఇచ్చినది Δ₁ = Δ₂
1 – cos²γ – cos²α – cos²β + 2 cos α cos β cos γ = 2 cos α cos β cos γ
1 – cos²α – cos²β – cos²γ = 0
1 = cos²α + cos²β + cos²γ

III.

Question 1.
\(\left|\begin{array}{ccc}
\mathbf{a}+\mathbf{b}+\mathbf{2 c} & \mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{b}+\mathbf{c}+\mathbf{2 a} & \mathbf{b} \\
\mathbf{c} & \mathbf{a} & \mathbf{c}+\mathbf{a}+\mathbf{2 b}
\end{array}\right|\) = 2(a + b + c)³ అని చూపండి.
Solution:

Question 2.
\(\left|\begin{array}{lll}
\mathbf{a} & \mathbf{b} & \mathbf{c} \\
\mathbf{b} & \mathbf{c} & \mathbf{a} \\
\mathbf{c} & \mathbf{a} & \mathbf{b}
\end{array}\right|^2\) = \(\left|\begin{array}{ccc}
2 b c-a^2 & c^2 & b^2 \\
c^2 & 2 a c-b^2 & a^2 \\
b^2 & a^2 & 2 a b-c^2
\end{array}\right|\) = (a³ + b³ + c³ – 3abc)² అని చూపండి. [Mar. ’01]
Solution:

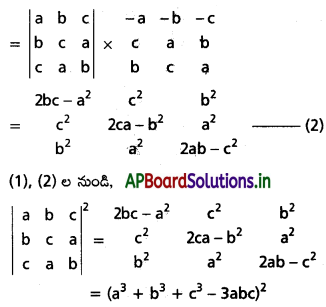
Question 3.
\(\left|\begin{array}{ccc}
a^2+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1)³ అని చూపండి. [Mar. ’13, ’07]
Solution:

= (a – 1)² [0(6 – 3) – 0[3(a + 1) – 3) + 1(a + 1 – 2)]
= (a – 1)² (a – 1)
= (a – 1)³
= R.H.S.

Question 4.
\(\left|\begin{array}{ccc}
a & b & c \\
a^2 & b^2 & c^2 \\
a^3 & b^3 & c^3
\end{array}\right|\) = abc (a – b) (b – c) (c – a) అని చూపండి. [May ’06]
Solution:

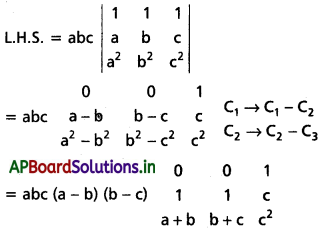
= abc (a – b) (b – c) [0(c² – c(b + c) – 0(c² – c(a + b) + 1(b + c – a – b)]
= abc (a – b) (b – c) (c – a)

Question 5.
\(\left|\begin{array}{ccc}
-2 a & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -2 \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|\) = 4(a + b) (b + c) (c + a) అని చూపండి.
Solution:

= 0 [∵ R₁ = R₃]
∴ (a + b), Δ కు కారణరాశి.
ఇదేవిధంగా b + c, c + a లు కూడా Δ కు కారణరాశులు.
∴ Δ అనునది a, b, c లలో 3వ పరిమాణం.
Δ = k(a + b) (b + c) (c + a), k శూన్యేతర సంఖ్య.
a = 1, b = 1, c = 1 అయిన
\(\left|\begin{array}{ccc}
-2 & 2 & 2 \\
2 & -2 & 2 \\
2 & 2 & -2
\end{array}\right|\) = k(1 + 1) (1 + 1) (1 + 1)
⇒ -2(4 – 4) – 2(-4 – 4) + 2(4 + 4) = 8k
⇒ 16 + 16 = 8k
⇒ k = 4
∴ Δ = 4(a + b) (b + c) (c + a)
∴ \(\left|\begin{array}{ccc}
-2 a & \mathbf{a}+\mathbf{b} & \mathbf{c}+\mathbf{a} \\
\mathbf{a}+\mathbf{b} & -2 \mathbf{b} & \mathbf{b}+\mathbf{c} \\
\mathbf{c}+\mathbf{a} & \mathbf{c}+\mathbf{b} & -2 \mathbf{c}
\end{array}\right|\) = 4(a + b) (b + c) (c + a).

Question 6.
\(\left|\begin{array}{ccc}
\mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} \\
\mathbf{b}-\mathbf{c} & \mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} \\
\mathbf{c}-\mathbf{a} & \mathbf{a}-\mathbf{b} & \mathbf{b}-\mathbf{c}
\end{array}\right|\) = 0 అని చూపండి.
Solution:

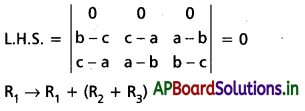
Question 7.
\(\left|\begin{array}{lll}
1 & a & a^2-b c \\
1 & b & b^2-c a \\
1 & c & c^2-a b
\end{array}\right|\) = 0 అని చూపండి.
Solution:

Question 8.
\(\left|\begin{array}{lll}
\mathbf{x} & \mathbf{a} & \mathbf{a} \\
\mathbf{a} & \mathbf{x} & \mathbf{a} \\
\mathbf{a} & \mathbf{a} & \mathbf{x}
\end{array}\right|\) = (x + 2a) (x – a)² అని చూపండి.
Solution:

= (x + 2a) [1(x – a)² – a(0(x – a) – 0)] + a[0 – 0(x – a)]
= (x + 2a) (x – a)²
= R.H.S.