Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 5 త్రిపరిమాణ నిరూపకాలు Exercise 5(b) will help students to clear their doubts quickly.
AP Inter 1st Year Maths 1B Solutions Chapter 5 త్రిపరిమాణ నిరూపకాలు Exercise 5(b)
అభ్యాసం – 5 (బి)
I.
ప్రశ్న 1.
A(-2, 3, 4), B(1, 2, 3) బిందువులను కలిపే రేఖాఖండాన్ని XZ – తలం విభజించే నిష్పత్తిని కనుక్కోండి.
సాధన:
AB ని XZ – తలం విభజించే నిష్పత్తి
AB = – y1 : y2 = -3 : 2
ప్రశ్న 2.
A (1, 1, 1), B (-2, 4, 1) బిందువులు రెండు శీర్షాలుగా, మూలబిందువు కేంద్రాభాసంగాగల త్రిభుజం ABC కి, శీర్షం ‘C’ నిరూపకాలు కనుక్కోండి. [T.S Mar. ’15]
సాధన:
A(1, 1, 1), B(-2, 4, 1) లు (x, y, z) బిందువు ∆ABC
యొక్క శీర్షాలు
Gబిందువు ∆ABC కేంద్రాభాసం
G నిరూపకాలు
\(\left(\frac{1-2+x}{3}, \frac{1+4+y}{3}, \frac{1+1+z}{3}\right)\) = (0, 0, 0)
\(\frac{x-1}{3}\) = 0, \(\frac{y+5}{3}\) = 0, \(\frac{z+2}{3}\) = 0
x – 1 = 0, y + 5 = 0, z + 2 = 0
x = 1
y = -5
z = -2
∴ నిరూపకాలు (1, -5, -2)
![]()
ప్రశ్న 3.
(3, 2, -1), (4, 1, 1), (6, 2,5) లు మూడు శీర్షాలుగా, (4, 2, 2) కేంద్రాభాసంగా గల చతుర్ముఖి నాలుగో శీర్షాన్ని కనుక్కోండి. [A.P Mar. 15, ’14; May’13, ’11, ’05 ]
సాధన:
A(3, 2, -1), B(4,1, 1), C(6, 2, 5), D(x, y, z) లు చతుర్భుజ శీర్షాలు
కేంద్రాభాసం G నిరూపకాలు
\(\left(\frac{3+4+6+x}{4}, \frac{2+1+2+y}{4}, \frac{-1+1+5+z}{4}\right)\)
= \(\left(\frac{13+x}{4}, \frac{5+y}{4}, \frac{5+z}{4}\right)\) = (4, 2, 2)
\(\frac{13+x}{4}\) = 4
13 + x = 16
x = 16 – 13 = 3
\(\frac{5+y}{4}\) = 2
5 + y = 8
y = 8 – 5 = 3
\(\frac{5+z}{4}\) = 2
5 + z = 8
z = 8 – 5 = 3
D నిరూపకాలు (3, 3, 3)
ప్రశ్న 4.
A = (6, 3, -4), B = (-2, −1, 2) లను కలిపే రేఖా ఖండం \(\overline{\mathrm{A B}}\) మధ్యబిందువుకూ, (3, -1, 2) బిందువుకూ మధ్య గల దూరాన్ని కనుక్కోండి.
సాధన:
A(6, 3, – 4) B(-2, -1, 2) లు దత్త బిందువులు.
AB మధ్య బిందువు Q.
Q నిరూపకాలు \(\left(\frac{6-2}{2}, \frac{3-1}{2}, \frac{-4+2}{2}\right)\)
= (2, 1, -1)
P నిరూపకాలు (3, -1, 2)
PQ = \(\sqrt{(3-2)^2+(-1-1)^2+(2+1)^2}\)
= \(\sqrt{1+4+9}=\sqrt{14}\) యూనిట్లు
![]()
II.
ప్రశ్న 1.
బిందువులు (5, 4, 2), (6, 2, −1), (8, −2, −7) సరేఖీయాలని చూపండి.
సాధన:
A(5, 4, 2), B(6, 2, −1) c(8, -2, -7) లు దత్త బిందువులు.

∴ A, B, C లు సరేఖీయాలు.
ప్రశ్న 2.
A(3, 2, 4), B(5, 4, – 6), C(9, 8, −10) ∞ సరేఖీయాలు అని చూపి, B, \(\overline{\mathrm{A C}}\) ని విభజించే నిష్పత్తిని కనుక్కోండి.
సాధన:
A(3, 2, – 4), B(5, 4, -6) మరియు C(9, 8, -10) లు దత్త బిందువులు
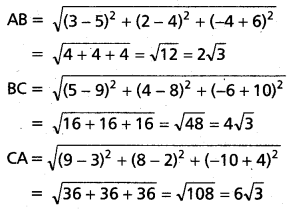
AB + BC = 2\(\sqrt{3}\) + 4\(\sqrt{3}\) = 6\(\sqrt{3}\) = CA
A, B, C లు సరేఖీయాలు
AC ని B విభజించే నిష్పత్తి = AB : BC
= 2\(\sqrt{3}\) : 4\(\sqrt{3}\)
= 1 : 2
![]()
III.
ప్రశ్న 1.
A(4, 8, 12), B(2, 4, 6), C(3, 5, 4), D(5, 8, 5) దత్త బిందువులైతే \(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) రేఖలు ఖండించుకొంటాయని చూపండి.
సాధన:
A(4, 8, 12), B(2, 4, 6) C (3, 5, 4) మరియు D(5, 8, 5) లు దత్త బిందువులు
AB ని λ : 1 నిష్పత్తిలో విభజించే బిందువు నిరూపకాలు
\(\left[\frac{2 \lambda+4}{\lambda+1}, \frac{4 \lambda+8}{\lambda+1}, \frac{6 \lambda+12}{\lambda+1}\right]\) ………………… (1)
CD ని μ : 1 నిష్పత్తిలో విభజించే బిందువు నిరూపకాలు
\(\left[\frac{5 \mu+3}{\mu+1}, \frac{8 \mu+5}{\mu+1}, \frac{5 \mu+4}{\mu+1}\right]\) ………………… (2)
దత్తరేఖలు ఖండించుకొంటే ఈ రెండు బిందువులు ఏకీభవించవలెను.
\(\frac{2 \lambda+4}{\lambda+1}\) = \(\frac{5 \mu+3}{\mu+1}\)
(2λ + 4) (μ + 1) = (5μ + 3) (λ + 1) ·
2λμ + 2λ + 4μ + 4 = 5λμ + 5μ + λ + 3
3λμ + λ + μ – 1 = 0
λ(3μ + 1) = -(μ – 1)
λ = – \(\frac{(\mu-1)}{3 \mu+1}\)
\(\frac{4 \lambda+8}{\lambda+1}\) = \(\frac{8 \mu+5}{\mu+1}\)
(4λ + 8) (μ + 1) = (8μ + 5) (λ + 1)
4λμ + 4λ + 8μ + 8 = 8λμ + 8μ + 5λ + 5
4λμ + λ – 3 = 0
(4μ + 1) λ = 3
–\(\frac{(4 \mu+1)(\mu-1)}{3 \mu+1}\) = 3
4μ2 – 4μ + μ – 1 = -9μ – 3
4μ2 + 6μ + 2 = 0
2μ2 + 3μ + 1 = 0
(2μ + 1) (μ + 1) = 0
μ = –\(\frac{1}{2}\) లేదా – 1
μ = -1 అసాధ్యం
μ = – \(\frac{1}{2}\)
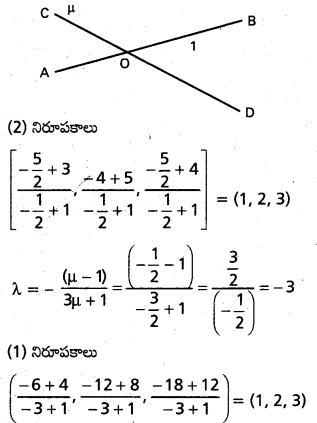
ఈ రెండు బిందువులు ఏకీభవిస్తున్నాయి కనుక దత్త రేఖలు ఖండించుకొంటున్నాయి.
![]()
ప్రశ్న 2.
A = (7, -6, 1), B = (17, -18,-3), C = (1, 4, -5), D = (3, -4, 11) లు దత్త బిందువులైతే \(\overleftrightarrow{A B}\), \(\overleftrightarrow{C D}\) ఖండన బిందువు కనుక్కోండి.

సాధన:
A(7, -6, 1), B(17, -18, -3), C(1, 4, -5) మరియు D(3, – 4,11) లు దత్త బిందువులు.
AB ని λ : 1 నిష్పత్తిలో విభజించే బిందు నిరూపకాలు
\(\left[\frac{17 \lambda+7}{\lambda+1}, \frac{-18 \lambda-6}{\lambda+1}, \frac{-3 \lambda+1}{\lambda+1}\right]\) ………………. (1)
CD ని μ : 1 నిష్పత్తిలో విభజించే బిందు నిరూపకాలు
\(\left[\frac{3 \lambda+1}{\mu+1}, \frac{-4 \mu+4}{\mu+1}, \frac{11 \mu-5}{\mu+1}\right]\) ………………… (2)
\(\frac{17 \lambda+7}{\lambda+1}\) = \(\frac{3 \mu+1}{\mu+1}\)
(17λ + 7) (μ + 1) = (3μ + 1) (λ + 1)
17λμ + 17λ + 7λ + 7 = 3λμ + 3λ + 2λ + 1
14λμ + 16λ +4μ + 6 = 0.
\(\frac{-18 \lambda-6}{\lambda+1}=\frac{-4 \mu+4}{\mu+1}\) ; \(\frac{-3 \lambda+1}{\lambda+1}=\frac{11 \mu-5}{\mu+1}\)
– 18λμ – 6μ – 18λ – 6
= -4λμ + 4λ – 4μ + 4
14λμ +22λ + 2μ + 10 = 0
14λμ +16λ +4μ + 6 = 0 ………………. (1)
14λμ + 22λ + 2μ + 10 = 0 …………….. (2)
తీసివేయగా -6λ + 2μ – 4 = 0
2μ = 6λ + 4
μ = 3λ +2
(1) లో ప్రతిక్షేపించగా
14λ (3λ + 2) + 16λ + 4(3λ + 2) + 6 = 0.
42λ2 + 28λ + 16λ + 12λ + 8 + 6 = 0
42λ2 +56λ + 14 = 0
3λ2 +4λ + 1 = 0
(λ + 1) (3λ + 1) = 0
λ = -1 లేదా λ = – \(\frac{1}{3}\)
λ = -1 అసాధ్యం
λ = – \(\frac{1}{3}\)
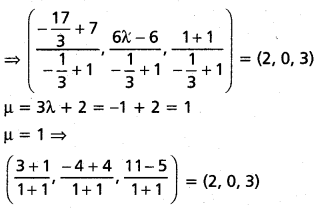
∴ ఈ రెండు బిందువులు ఒకటే
AB, CD రేఖలు ఖండించుకొంటున్నాయి.
ఖండన బిందువు (2, 0, 3)
![]()
ప్రశ్న 3.
A(3, 2, 0), B(5, 3, 2), C(-9, 6, -3) లు ఒక త్రిభుజం శీర్షాలు, ∠BAC యొక్క కోణసమద్విఖండన రేఖ \(\overline{\mathrm{A D}}\), \(\overline{\mathrm{B C}}\) ని D వద్ద ఖండిస్తుంది. D యొక్క నిరూపకాలు కనుక్కోండి.
సాధన:
A(3, 2, 0), B(5, 3, 2) C(-9, 6, -3) లు ∆ABC శీర్షాలు
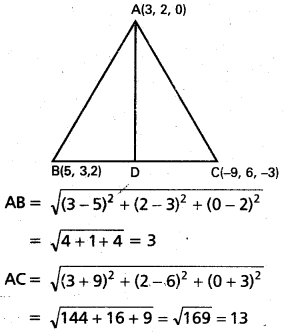
AB రేఖ ∠DAC కోణ సమద్విఖండన రేఖ
‘D’ బిందువు BC ని 3 : 13 నిష్పత్తిలో విభజిస్తున్నాయి.
P నిరూపకాలు
\(\left(\frac{3(-9)+13.5}{3+13}, \frac{3.6+13.3}{3+13}, \frac{3(-3)+13.2}{3+13}\right)\)
= \(\left(\frac{38}{16}, \frac{57}{16}, \frac{17}{16}\right)\)
![]()
ప్రశ్న 4.
O(0, 0, 0), A(2, -3, 3), B(-2, 3, -3) Dox సరేఖీయాలని చూపండి. ప్రతిబిందువూ మిగిలిన రెండు బిందువులను కలిపే రేఖను ఏ నిష్పత్తిలో విభజిస్తుందో కనుక్కోండి.
సాధన:
0(0, 0, 0), A(2, -3, 3), B(-2, 3, -3) లు దత్త బిందువులు

∴ O, A, B లు సరేఖీయాలు.
![]()
AB ని ‘O’ విభజించే నిష్పత్తి
= OA: OB
= \(\sqrt{22}\) : \(\sqrt{22}\) = 1 : 1
OB ని A విభజించే నిష్పత్తి
= OA: AB = \(\sqrt{22}\) : 2 \(\sqrt{22}\) = -1 : 2
OA ని B విభజించే నిష్పత్తి
= -AB : BO = − 2\(\sqrt{22}\): \(\sqrt{22}\) – 2\(\sqrt{22}\) : \(\sqrt{22}\) = -2 : 1.