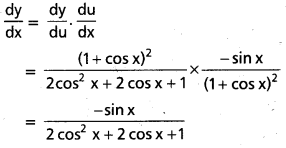AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Ex 9(b)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 9 అవకలనం Exercise 9(b) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 9 అవకలనం Exercise 9(b)

అభ్యాసం 9 (బి)

I.

ప్రశ్న 1.
కింది ప్రమేయాల అవకలజాలను కనుక్కోండి.

i) cotⁿ x
సాధన:
f(x) = cotⁿ x, \(\frac{d y}{d x}\) = n. cot^n-1x.\(\frac{\mathrm{d}}{\mathrm{dx}}\)(cot x)
= n. cot^{n -1} x (- cosec² x)
= – n. cot^{n -1}x. cosec² x

ii) cosec⁴ x
\(\frac{d y}{d x}\) = 4. cosec³ x. \(\frac{\mathrm{d}}{\mathrm{dx}}\) (cosec x)
= 4. cosec³ x (- cosec x. cot x)
= -4. cosec⁴ x. cot x

iii) tan (e^x)
సాధన:
f(x) = tan (e^x)
\(\frac{d y}{d x}\) = sec² (e^x). (e^x)¹ = e^x. sec² (e^x)

iv) \(\frac{1-\cos 2 x}{1+\cos 2 x}\)
సాధన:

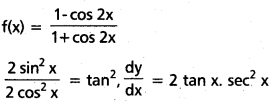
v)
sin^mx. cosⁿx
సాధన:
f(x) = sin^mx. cosⁿx
\(\frac{d y}{d x}\) = (sin^mx). \(\frac{\mathrm{d}}{\mathrm{dx}}\)(cosⁿx)\(\frac{\mathrm{d}}{\mathrm{dx}}\)(sin^mx)
= sin^mxn cos^{n – 1}x(-sin x) + cosⁿx. m sin^{m – 1}x. cos x
= m. cos^{n + 1}x. sin^{m – 1}x – n. sin^{m + 1} x. cos^{n – 1}x.

vi) sin mx. cos nx
సాధన:
f(x) = sin mx. cos nx
\(\frac{d y}{d x}\) = sin mx \(\frac{d}{d x}\)(cos nx) + (cos nx)\(\frac{d}{d x}\)(sin mx)
= sin mx (-n sin nx) + cos nx (m cos mx)
= m. cos mx. cos nx – n. sin mx. sin nx

vii) x tan^-1 x
సాధన:
f(x) = x tan^-1x\(\frac{d y}{d x}\)
= x.\(\frac{\mathrm{d}}{\mathrm{dx}}\) (tan^-1x) + (tan^-1 x)\(\frac{d}{d x}(x)\)
= \(\frac{x}{1+x^2}\) + tan^-1x

viii) sin^-1 (cos x)
సాధన:
f(x) = sin^-1(cos x) = sin^-1\(\left[\sin \left(\frac{\pi}{2}-x\right)\right]\) = \(\frac{\pi}{2}\) – x
\(\frac{d y}{d x}\) = 0 – 1 = -1

ix) log (tan 5x)
సాధన:
f(x) = log (tan 5x)

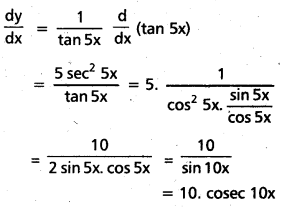
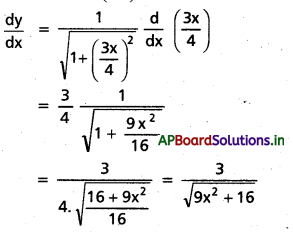
x) sinh^-1\(\left(\frac{3 x}{4}\right)\)
సాధన:
f(x) = sinh^-1\(\left(\frac{3 x}{4}\right)\)

xi) tan^-1 (log x)
సాధన:
f(x) = tan^-1(log x)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = \(\frac{1}{1+(\log x)^2}\).\(\frac{d}{d x}(\log x)\)
= \(\frac{1}{x\left(1+(\log x)^2\right)}\)

xii) log \(\left(\frac{x^2+x+2}{x^2-x+2}\right)\) (May ’06)
సాధన:

xiii) log (sin^-1(e^x))
సాధన:
f(x) = log(sin^-1(e^x))

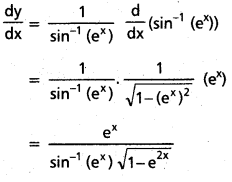
xiv) (sin x)²(sin^-1x)²
సాధన:
f(x) = (sin x)²(sin^-1x)²

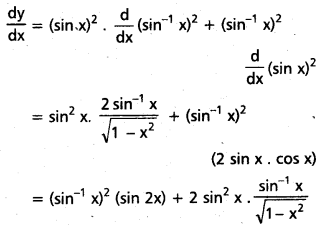
xv) \(\frac{\cos x}{\sin x+\cos x}\)
సాధన:

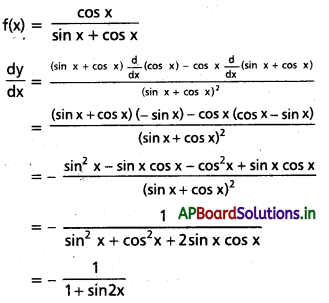
xvi) \(\frac{x\left(1+x^2\right)}{\sqrt{1-x^2}}\)
సాధన:

xvii) \(e^{\sin ^{-1} x}\)
సాధన:

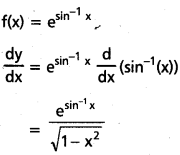
xviii) cos (log x + e^x)
సాధన:
f(x) = cos (log x + e^x)
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = – sin (log x + e^x) \(\frac{d}{d x}\)(log x + e^x)
= – sin (log x + e^x)(\(\frac{1}{x}\) + e^x)

xix) \(\frac{\sin (x+a)}{\cos x}\)
సాధన:

xx) cot^-1 (cosec 3x)
సాధన:
f(x) = cot^-1 (cosec 3x)

ప్రశ్న 2.
x దృష్ట్యా క్రింది వాటి అవకలజాలను కనుక్కోండి.

i) x = sinh² y
సాధన:
f(x) = x = sinh² y
\(\frac{d x}{d y}\) = 2 sinh y . cosh y

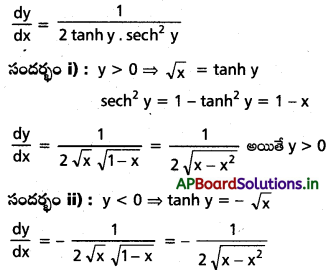
ii) x = tanh^{2/sup> y
సాధన:
f(x) = tanh2/sup> y. \(\frac{d x}{d y}\) = 2 tanh y. sech2 y}

iii) x = e^{sinh y}
సాధన:
\(\frac{d x}{d y}\) = e^{sinh y}\(\frac{d}{d x}(\sinh y)\)
= e^{sinh y}. cosh y
= x . cosh y
\(\frac{d y}{d x}\) = \(\frac{1}{\left(\frac{d x}{d y}\right)}\) = \(\frac{1}{x \cdot \cosh y}\)

iv) x = tan (e^-y)
సాధన:

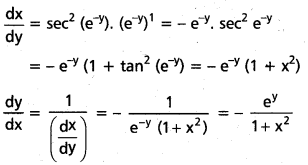
v) x = log (1 + sin² y)
సాధన:

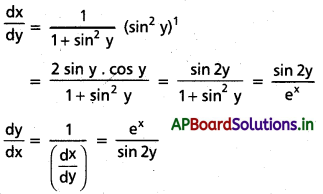
vi) x = log (1 + \(\sqrt{\mathbf{y}}\))
సాధన:
1 + \(\sqrt{\mathbf{y}}\) = e^x
\(\sqrt{\mathbf{y}}\) = e^x – 1
y = (e^x – 1)²
\(\frac{d y}{d x}\) = 2(e^x – 1). e^x = 2\(\sqrt{y}\). e^x
= 2\(\sqrt{y}\) (\(\sqrt{y}\) + 1)
= 2(y + \(\sqrt{y}\))

II. కింది ప్రమేయాల అవకాలను కనుక్కోండి

i) y = cos (log (cot x))
సాధన:
y = cos (log (cot x))

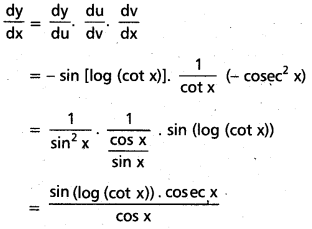
ii) sinh^-1 \(\left(\frac{1-x}{1+x}\right)\)
సాధన:
y = sinh^-1\(\left(\frac{1-x}{1+x}\right)\)
సందర్బ౦: 1. x < -1

సందర్బ౦: 2. x > -1

iii) log (cot(1 – x²))
సాధన:
y = log (cot(1 – x²))

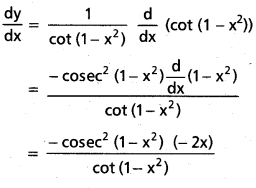
iv) sin (cos (x²))
సాధన:
y = sin (cos (x²))
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) = cos (cos (x²)). \(\frac{\mathrm{d}}{\mathrm{dx}}\) (cos (x²))
= cos (cos (x²)) (-sin (x²)). \(\frac{d}{d x}\)(x²)
= -2x. sin (x²). cos (cos (x²))

v) sin (tan^-1 (e^x))
సాధన:
y = sin (tan^-1 (e^x)
\(\frac{d y}{d x}\) = cos (tan^-1(e^x)). \(\frac{d}{d x}\)(tan^-1(e^x))
= cos(tan^-1(e^x)) . \(\left[\frac{1}{1+\left(e^x\right)^2}\right]\)(e^x)
= \(\frac{e^x}{1+e^{2 x}}\). cos(tan^-1(e^x))

vi) \(\frac{\sin (a x+b)}{\cos (c x+d)}\)
సాధన:

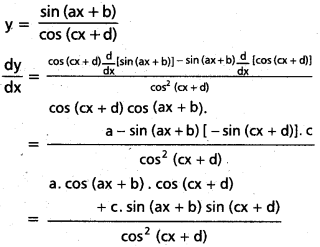
vii) tan^-1\(\left[\tanh \left[\frac{x}{2}\right]\right]\)
సాధన:
y = tan^-1 \(\left[\tanh \left[\frac{x}{2}\right]\right]\)

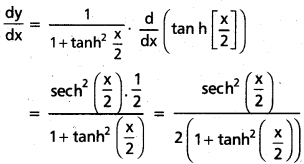
viii)
sin x. (Tan^-1 x)²
సాధన:
y = sin x. (Tan^-1 x)²

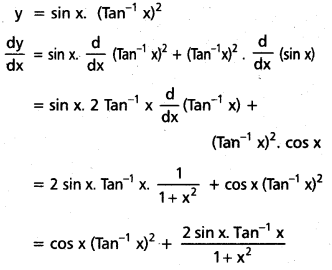
III. కింది ప్రమేయాల అవకలజాలను కనుక్కోండి.

ప్రశ్న 1.
sin^-1 \(\left(\frac{\mathbf{b}+\mathbf{a} \sin x}{\mathbf{a}+\mathbf{b} \sin x}\right)\) (a > 0, b > 0)
సాధన:

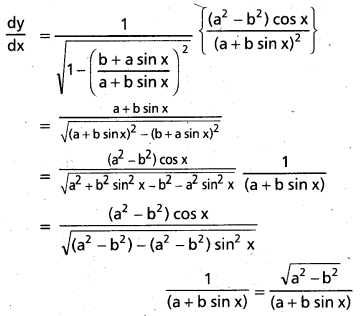
ప్రశ్న 2.
cos^-1\(\left(\frac{b+a \cos x}{a+b \cos x}\right)\) (a > 0, b > 0)
సాధన:

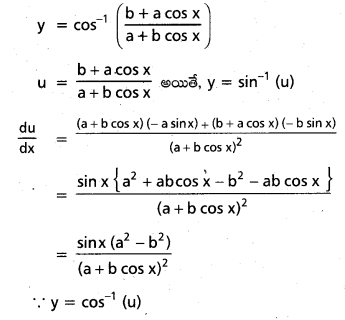
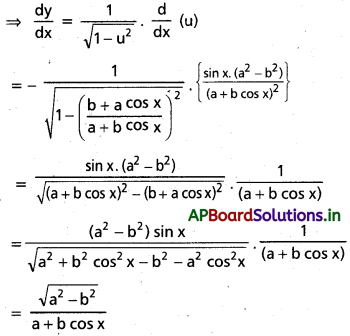
ప్రశ్న 3.
Tan^-1 \(\left[\frac{\cos x}{1+\cos x}\right]\)
సాధన: